弹载单基测角被动定位滤波算法研究

张记华，韦亚利，李 智，周小川

（上海机电工程研究所，上海 201109）

0 引 言

在现代高技术作战中，无源探测定位具有隐蔽性好、作用距离远、防区外实施等优点，为先敌发现、先敌攻击创造了有利条件。

无源探测定位技术是利用目标辐射源的辐射信息探测目标，并确定目标位置的一种技术。在导弹攻防对抗中，利用无源探测定位技术，能在敌方防区外探测并定位目标，出其不意地对目标发起攻击，实现远程、主动、精确打击目标。在短兵相接的伏击战中，利用无源探测定位技术能快速定位目标，即使敌方雷达关机，仍具备有效打击目标的能力，实现对目标的防守反击。目前，美国最新的AGM－88E先进反辐射导弹是在“哈姆”基础上改进而来的，只要敌方雷达短暂开机，就能够快速捕捉并定位目标，具备很强的抗目标雷达关机能力。

快速无源探测定位的技术需求是当目标对外辐射信息（雷达、导航、通信）时，在有限的时间内快速完成目标定位；其局限性是当目标不对外辐射信息时，无法实施无源探测定位。

根据定位站点分类，无源定位可分为单站定位和多站定位，站点可以是静止的也可以是运动的；根据目标运动情况分类，无源定位可分为对静止目标的定位和对运动目标的定位。

本文研究运动单站对静止目标的无源定位方法，利用单个运动平台（被动导引头）对辐射源角度的连续测量，通过弹载信息处理手段，实现对辐射源目标的高精度定位，简称弹载单基测角被动定位技术。

1 系统建模

在发射点当地地理坐标系内，假设目标静止不动，弹目相对位置关系如图1所示。

图1 导弹和目标相对位置Fig．1 Relative position of missile and target

选取弹目相对位置为状态变量，导引头测角信息为观测量，弹目相对位置增量为控制量，则系统状态方程和观测方程为

已知被动测角信息 （qε，qβ）和导弹位置信息 （xM，yM，zM），由约束方程h（X）求解出状态变量X，即可获得目标位置信息 （xT，yT，zT），因此目标定位的实质可以转化为非线性方程最优求解或者状态最优滤波估计问题。

2 滤波算法

状态滤波估计算法通常分为批处理法和序列滤波法。批处理法是指将按时间顺序排列的测量数据集合在一起进行最优估计。典型的批处理方法有最大似然估计法（maximum likelihood estimation，MLF）、非线性 最 小 二 乘 法 （nonlinear least square method，NLS）和 伪 线 性 估 计 法 （pseudo linear estimation，PLE）。考虑数据处理实时性、计算量和存储空间等因素，批处理法通常转化为递推方式，例如递推最小二乘法（recursive least square method，RLS）。序列滤波方法是指将每次获得的测量数据作为滤波器的输入进行实时计算处理。相对于批处理方法，序列滤波方法具有计算量小、存储空间少等优点，例如扩展卡尔曼滤波法（extended Kalman filter method，EKF）、无迹卡 尔 曼 滤 波 法 （unscented Kalman filter method，UKF）、自适应扩展卡尔曼滤波法（adaptive extended Kalman filter method，AEKF）、有限差分扩展卡尔曼滤波法（finite difference extended Kalman filter method，FDEKF）等。

卡尔曼滤波在导航和制导信息处理方面应用广泛［1］。文献［2］基于单基测角制导体制，针对机载单站无源定位的精度和实时性问题，提出了一种基于角度信息的递推最小二乘（RLS）无源定位算法；文献［3］针对单站无源定位，提出了一种基于CV模型的卡尔曼滤波算法（EKF）；文献［4］采用无迹卡尔曼算法（UKF）对抗雷达关机技术进行了研究；文献［5］在导引头测量信号包含有色噪声条件下，提出了采用观测方程重构思想的被动滤波算法；文献［6］研究了有限差分卡尔曼滤波（FDEKF）方法在目标雷达被动定位中的应用；文献［7］针对纯方位目标运动分析中扩展卡尔曼滤波算法易发散的不足，提出了一种自适应卡尔曼滤波算法，利用极大后验噪声估计器Sage＿Husa对虚拟观测噪声进行实时在线估计，动态补偿线性化带来的误差。

滤波处理的核心是非线性问题的次优近似，通常采用非线性环节线性化的方法或者采样近似非线性分布的方法。实现非线性环节线性化，可以采用Taylor级数展开，取有限项截断，也可以采用伪线性化方法，通过恒等变换，将非线性函数映射为线性函数。实现采样近似非线性分布，通常采用近似非线性函数的概率密度法。

下面分别选取递推最小二乘法（RLS）、扩展卡尔曼滤波法（EKF）、无迹卡尔曼滤波法（UKF）、有限差分扩展卡尔曼滤波法（FDEKF）、自适应扩展卡尔曼滤波法（AEKF）进行算法分析。

2．1 递推最小二乘法（RLS）算法

递推最小二乘法的实质是将系统状态观测方程重写为目标位置估计的状态方程，如式（3）所示。每获得一次数据，就更新一次状态方程参数估计值。随着观测数据的增多，就能获得满意的状态估计值。相对于批数据处理最小二乘法，递推最小二乘法大大减少了计算量和存储量，能够实现在线实时估计。

根据三角函数变换关系，系统观测方程可重写为

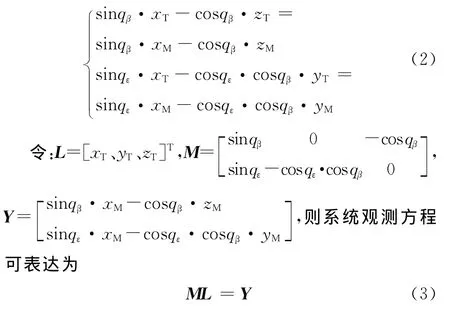
当观测矩阵M可逆时，系统状态可观测，且具有唯一解，递推最小二乘算法实现如下。

式中：I2和I3为单位矩阵；k为迭代递推次数。

b）更新估计状态信息

2．2 扩展卡尔曼滤波法（EKF）算法

卡尔曼提出的滤波理论只适用于线性系统，BUCY等提出并研究了扩展卡尔曼滤波（EKF）［8］，将卡尔曼滤波理论进一步应用到非线性领域。EKF的基本思想是将非线性系统线性化，然后进行卡尔曼滤波，因此EKF是一种次优滤波。

将非线性函数Taylor展开，保留一次项，令H（k＋1）＝｜＾（／），EKF递推算法如式（6）所示。Xk＋1k

2．3 无迹卡尔曼滤波法（UKF）算法

EKF方法通过对非线性函数进行Taylor展开，取其一次项近似原函数。由于忽略了高阶项，当系统非线性强时，线性化会使系统产生较大的误差，甚至滤波发散。JULIER等提出了一种无迹卡尔曼滤波算法［9］，此方法摒弃了对非线性函数进行线性化的传统做法，采用卡尔曼线性滤波框架，对于一步预测方程，使用无迹变换（unscented transform，UT）来处理均值和协方差的非线性传递问题。

UT变换原理为在原状态分布中按某一规则选取一些采样点，使这些采样点的均值和协方差等于原状态分布的均值和协方差；将这些点代入非线性函数中，得到相应非线性函数值的点集，通过这些点集求取变换后的均值和协方差。这样得到的非线性变换后的均值和协方差精度最少具有2阶精度（Taylor级数展开），对于高斯分布，可达到3阶精度。其采样点的选择是基于先验均值和先验协方差矩阵的相关列实现的。

式中：λ＝α1（N＋j）－N为比例缩放参数，j的选择一般使之满足N＋j＝3，α1用于控制采样点分布的距离，0≤α1≤1，一般取较小的数值；对于正态分布，一般取α2＝2；（）i是 （N＋λ的平方根矩阵的第i行（列），可以利用Cholesky分解进行计算；Wi是第i个采样点Xi的权值，并有＝1。

确定了采样点就可以求取状态和观测量的均值估计值和协方差估计值，该精度可以达到Taylor展开的二次项，UKF的递推算法与EKF类似，这里不再赘述。

2．4 有限差分扩展卡尔曼滤波法（FDEKF）算法

有限差分扩展卡尔曼滤波（FDEKF）是扩展卡尔曼滤波（EKF）的一种改进算法，其实质就是应用有限差分代替非线性函数的偏导计算，其精度高于Taylor级数的一阶展开，对模型参数变动具有较强的鲁棒性，并且适用于各种非线性函数。

对EKF中的矩阵P进行Cholesky分解，如式（8）所示。

利用一阶中心差分计算非线性观测方程的偏导数，如式（9）所示。

FDEKF的递推算法详见文献［6］，这里不再赘述。

2．5 自适应扩展卡尔曼滤波法（AEKF）算法

扩展卡尔曼滤波算法要求知道先验的噪声统计，然而有时噪声的统计特性是未知的或不准确的，甚至可能是时变的。错误的噪声统计会产生滤波误差，甚至使滤波发散，这也正是EKF的局限性。利用虚拟噪声技术，非线性系统的线性化误差在一定程度上可以归为线性系统模型中的一种噪声。因此，用自适应滤波在线估计虚拟噪声的统计特性，可以降低线性化误差，提高非线性滤波的精度。

非线性函数线性化过程与扩展卡尔曼的线性化过程相同，这里不再赘述。对于时变噪声特性，应强调新近数据的作用，逐渐遗忘过去的数据［7］。引入遗忘因子d，采用渐消记忆方法实现改进的时变噪声统计估值器。

AEKF与EKF的递推算法区别在于预测观测量噪声协方差矩阵不同，AEKF的预测观测量噪声协方差矩阵如式（10）所示。

式中，dk＝，b取值范围0～1，通常取值0．95。

3 仿真分析

3．1 被动测角误差模型

被动测量误差包括两类：系统噪声误差和测角零位误差，比相测角体制的理论误差模型描述如式（11）所示。

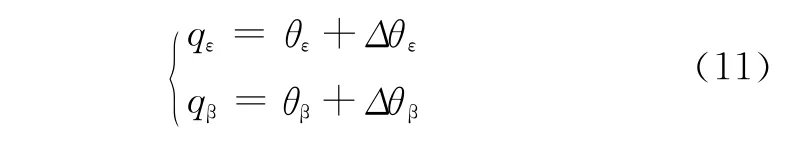
式中：（θε，θβ）为理论计算值；（Δθε，Δθβ）为由测角零位和系统噪声引起的测量误差值。

依据上述理论模型，给出了典型频点被动测角的理论计算值和含测角误差的理论测量值，如图2所示。

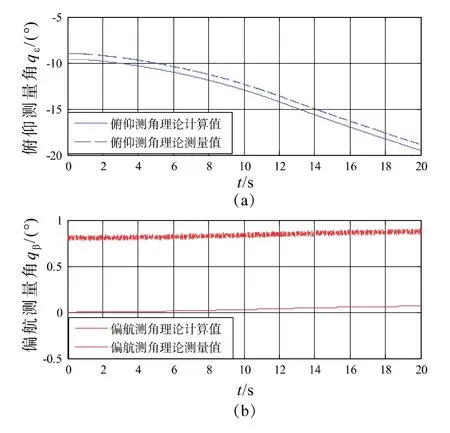
图2 被动测角理论计算值和理论测量值Fig．2 Theoretical true value and theoretical measurement value of passive angle measurement

3．2 仿真结果

假设目标位置为（59 161．0，5．0，0．0），导弹纵向平面弹道曲线如图3所示。

图3 纵向平面弹道曲线Fig．3 Longitudinal plane ballistic curve

基于理论被动测角误差模型和上述运动轨迹，分别采用递推最小二乘法（RLS）、扩展卡尔曼滤波法（EKF）、无迹卡尔曼滤波法（UKF）、有限差分扩展卡尔曼滤波法（FDEKF）、自适应扩展卡尔曼滤波法（AEKF）等进行仿真分析。

以AEKF为例，仿真分析情况如下。

1）初值估计的影响

图4给出了不同估计初值误差下AEKF的仿真结果。估计初值误差越大，收敛时间越短；估计初值误差越小，收敛时间越长。这说明估计初值误差对定位收敛时间影响较大。

估计初值误差对收敛精度也有不同程度的影响，大体趋势表现为初值估计误差越大。收敛精度越差。图4中紫色线条表示定位误差为5%，这是指标要求。

图4 不同初值误差仿真结果（AEKF）Fig．4 Simulation results of different initial value errors（AEKF）

2）测量误差大小的影响

图5给出了不同测量误差的仿真结果。不同测量误差对AEKF收敛时间影响不大，主要影响收敛精度。测量误差越小，收敛精度越高；测量误差越大，收敛精度越低。图中紫色线条表示定位误差为5%，这是指标要求。

图5 不同测量误差仿真结果（AEKF）Fig．5 Simulation results of different measurement errors（AEKF）

3）采样周期的影响

图6给出了不同采样周期下的仿真结果。采样周期越短，AEKF的收敛时间越短，收敛精度也高；采样周期越长，AEKF的收敛时间越长，收敛精度也越差。图中紫色线条表示定位误差为5%，这是指标要求。

图6 不同采样周期仿真结果（AEKF）Fig．6 Simulation results of different sampling periods（AEKF）

4）观测量噪声的影响

若观测量噪声的统计特性未知或不准确，自适应扩展卡尔曼滤波仍然收敛，鲁棒性强，如图7所示。图中紫色线条表示定位误差为5%，这是指标要求。

图7 不同测量噪声协方差矩阵的仿真结果（AEKF）Fig．7 Simulation results of covariance matrix of different measurement（AEKF）

3．3 综合评价

结合工程应用实际，从线性化精度（4分）、初值估计误差的影响（1．5分）、测量误差大小的影响（1．0分）、采样周期的影响（0．5分）、测量噪声的影响（2．0分）以及算法复杂度（1．0分）等方面进行综合评价，综合分析不同滤波算法的仿真结果，评价结果如表1所示。

表1 非线性滤波算法综合评价结果Table．1 Comprehensive evaluation results of nonlinear filtering algorithm

由表1可知：

1）得分较高的是RLS和AEKF，分别为7．3和7．0，得分高的原因是其鲁棒性强；

2）得分次之的是UKF和FDEKF，得分均为6．3，UKF线性化精度高但算法复杂，而FDEKF算法简单且线性化精度不差；

3）得分最低的是EKF，原因是线性化精度和鲁棒性均不突出。

4 结束语

本文以弹载单基测角被动定位为例，构建了系统状态方程和观测方程，将被动定位问题转换为状态滤波最优估计问题，理论分析了不同非线性滤波算法的原理，并给出递推算法模型。结合工程实例，开展了仿真分析工作，从线性化精度、初值误差估计、测量误差、采用周期、观测噪声以及算法复杂度等方面进行了综合评分，得出了递推最小二乘法和自适应扩展卡尔曼滤波算法得分较高的结论。