基于非定常面元法的海上浮式风机气动性能研究

刘利琴，陈迪郁，沈文君，李 昊，邓万如

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072； 2. 交通运输部天津水运工程科学研究所 工程泥沙交通行业重点实验室，天津 300456)

叶片是风力机的关键部件，其表面形状对整个风机的空气动力学性能和风力机的风能利用率都会产生重要的影响，因此叶片的气动性能一直都是风力机的研究重点。为评估风力发电机效率和结构安全，需要正确预估不同来流条件下叶片上的风载荷。特别是在研究海上浮式风机时，自身的绕流情况会变得更为复杂。为了提高风能的利用效率，必须要准确快速地解决风机面临的空气动力学问题。

目前计算风机气动载荷的常用方法主要有叶素动量理论(BEM)、三维势流理论、计算流体力学(CFD)方法。其中，叶素动量理论基于工程经验提出，计算速度快，但不能很好地考虑风力机流场尾流特性；计算流体力学(CFD)方法可以准确地考虑流场黏性及尾流，但计算速度非常慢，难以用于大规模工程计算；基于三维势流理论的面元法计算风力机气动载荷逐渐受到人们的重视。该方法最早应用于模拟飞机机翼的空气动力学，Hess和Smith[1]首次采用面元法来计算无升力体的流体动力，为面元法理论奠定了基础。与叶素动量法和计算流体力学方法相比，面元法能在较少的时间内获得较高的计算精度[2]。作为一种数值求解方法，面元法可以真实地模拟叶片的几何形状，并在表面上满足边界条件，将问题简化为计算物体表面奇点单元的强度，不需要对整个流场进行求解，从计算的角度来看具有更高的经济性和实用性[3]。近年来有不少学者将面元法拓展到风力机叶片的气动性能计算上，并且成功得到了应用。Bermúdez等[4]开发了基于三维低阶非定常速度势的面元法求解器，对NREL水平轴风力机进行了数值模拟，和试验测试的结果对比表明该求解器可以很好地模拟非定常效应并作为工程设计软件使用。Tescione等[5]基于自由尾涡/面元法模拟了垂直轴风力机的三维气动性能，通过和垂直轴风机试验数据对比，验证了自由涡尾流模型的正确性，并且该数值模型在已经观察到的中心收缩和侧向膨胀的情况下，可以很好地捕获水平面中涡旋结构的动力学行为以及尖端涡旋的垂直运动。刘洋等[6]基于三维速度势面元法来估算风机的三维非定常气动力，计算值和试验数据对比良好，证明该方法在贴体流动和小分离工况下具有较好的适用性。周捍珑等[7]以面元法理论为基础，MEXICO风轮模型和试验数据为支撑，对风力机的偏航性能进行了预测。近年来，海上浮式风力机发展迅速，并逐步商业化。由于海洋环境复杂，且浮式基础运动将影响风力机的气动载荷，因而海上浮式风力机气动载荷研究更加重要。Netzband等[8]将面元法应用到海上浮式风力发电机的气动力和水动力计算，针对浮式基础的运动展开研究，风机的定常以及非定常模拟结果和3种不同的雷诺平均N-S方程(RANS)计算结果具有一致性。

基于非定常面元法，重点研究海上浮式风力机气动载荷特性，开发了水平轴风机定常及非定常气动载荷的计算程序，考虑剪切风、塔影效应以及浮式基础运动，进一步研究了浮式基础运动对风力机气动载荷的影响。

1 面元法基本理论

1.1 基本方程

风力机叶片的表面边界SB是已知的，如图1所示，当风力机处于流场中时，总的速度势符合拉普拉斯方程，用不可压缩无旋连续性方程来表示：

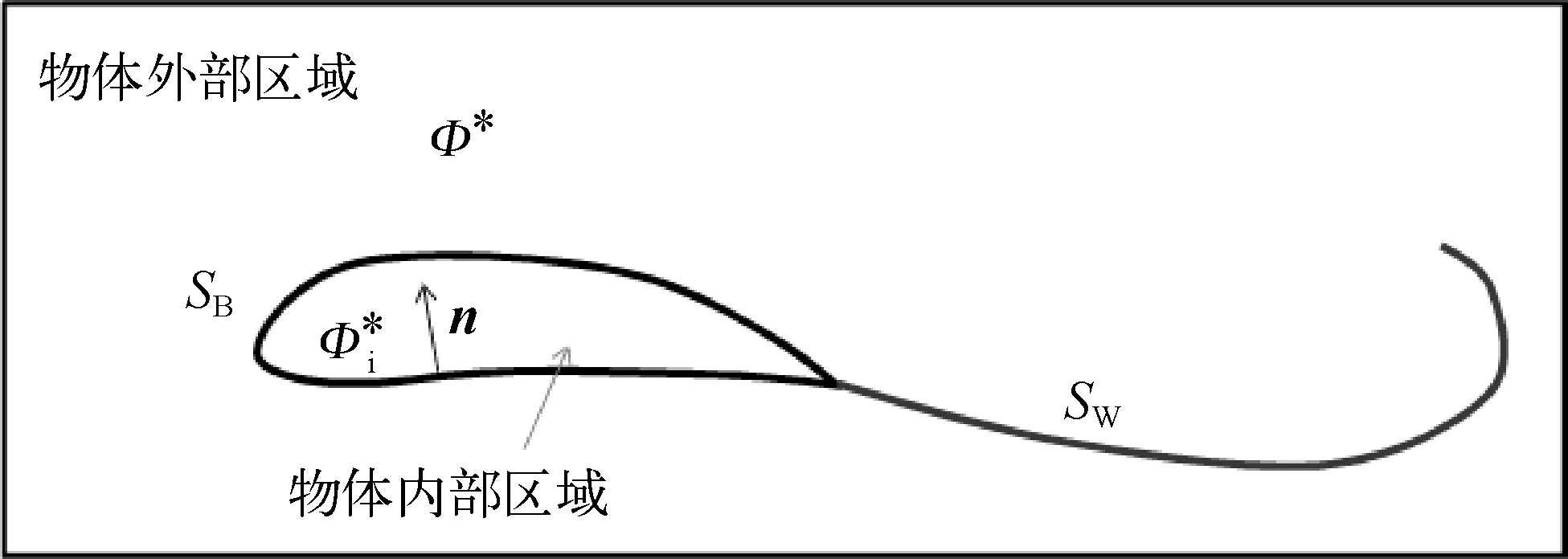
图1 计算空间的流场示意Fig. 1 Potential flow of computational domain

(1)

根据格林公式，在物面SB上分布一系列的源σ和偶极子μ来构造求解方程。源用于模拟风力机叶片厚度带来的影响，而反对称项例如偶极子(或涡)则用于解决升力问题。对于一般的三维势流情况，还需要考虑尾流的建模、尾流脱落初始方向和几何形状。因此在尾流上也布置偶极子，这样可以将方程转化成积分的形式[9]：

(2)

式中:n为指向物体内部的法向量；r为点(x,y,z)到奇点面元的距离；Φ∞为无穷来流的速度势。

内外速度势之间的差异定义为偶极子的强度：

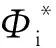
(3)

内外速度势在法向上求导的差值定义为源的强度：

(4)

1.2 边界条件

直接在表面边界上指定法向速度为0的方程称为Neumann边界条件，而在边界上给定速度势的大小间接使得法向速度分量等于0，这样的边界条件称为Dirichlet边界条件。基于速度势的面元法进行分析，故采用Dirichlet边界条件，物面SB内部的速度势是常量：

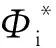
(5)

物体内部存在的速度势为：

(6)

上述方程是间接满足边界条件的基础(其中SW表示尾流区域)，但是该常数取不同的值也会产生不同的解法，例如假设该常数等于0，速度势函数将会包括Φ∞这一项，奇点的强度就会特别大。这里不妨假设该常数等于Φ∞，这样结合方程(5)和方程(6)，问题简化为扰动产生的速度势为0。

(7)

σ=n·V∞

(8)

为了进一步求解SB上未知的偶极子强度和尾流上的偶极子分布，将物体表面SB离散成若干个单元，在离散时，采用四边形面元，每个面元上均匀分布常值面源和面偶极子，取面元的中心为控制点(见图2)，物面上的面元数量设为N，尾流的面元数量设为NW，在每一时刻方程(7)离散为一组关于μ和μl的代数方程：

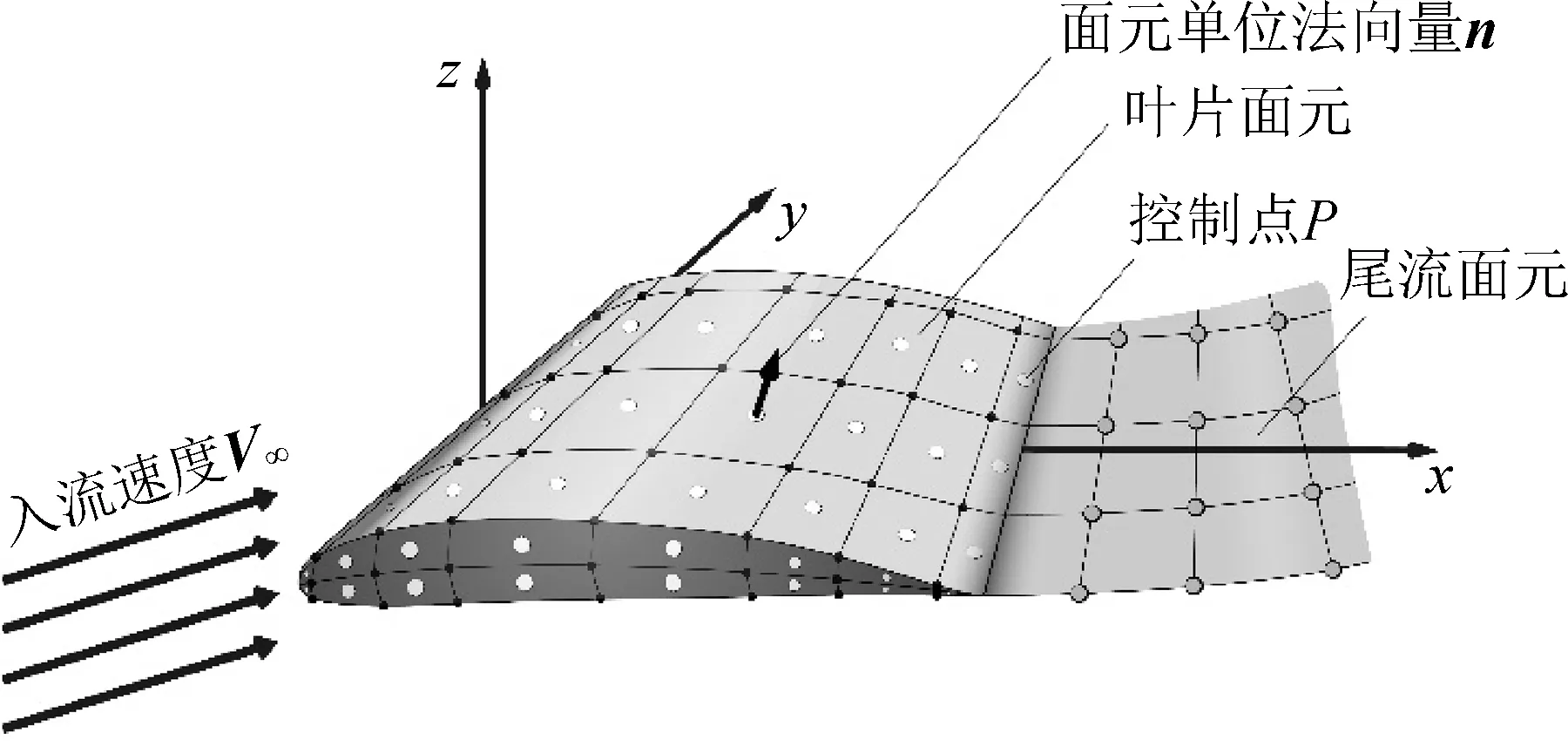
图2 叶片表面的面元分布Fig. 2 Panel distribution on blade surface

(9)

其中，Ck、Cl和Bk称为影响系数，采用面元局部坐标系(图3)进行计算，使用它们与强度的乘积来表示奇点产生的速度势：

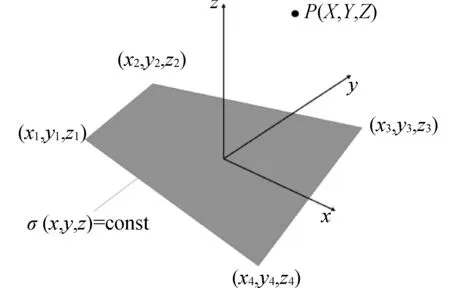
图3 面元坐标系示意Fig. 3 Schematic diagram of panel coordinate system

(10)

(11)

2 数值离散模型

2.1 叶片及尾流模型

选取NREL 5 MW风机[10]作为计算对象，该风机是三叶片水平轴风力机，叶型采用DU和NACA系列翼型。根据叶片的几何参数进行建模并划分网格，为了提高计算的准确性，在弦长方向上划分30个网格，展长方向网格数为50，最后一共得到1 500个面元，如图4所示。

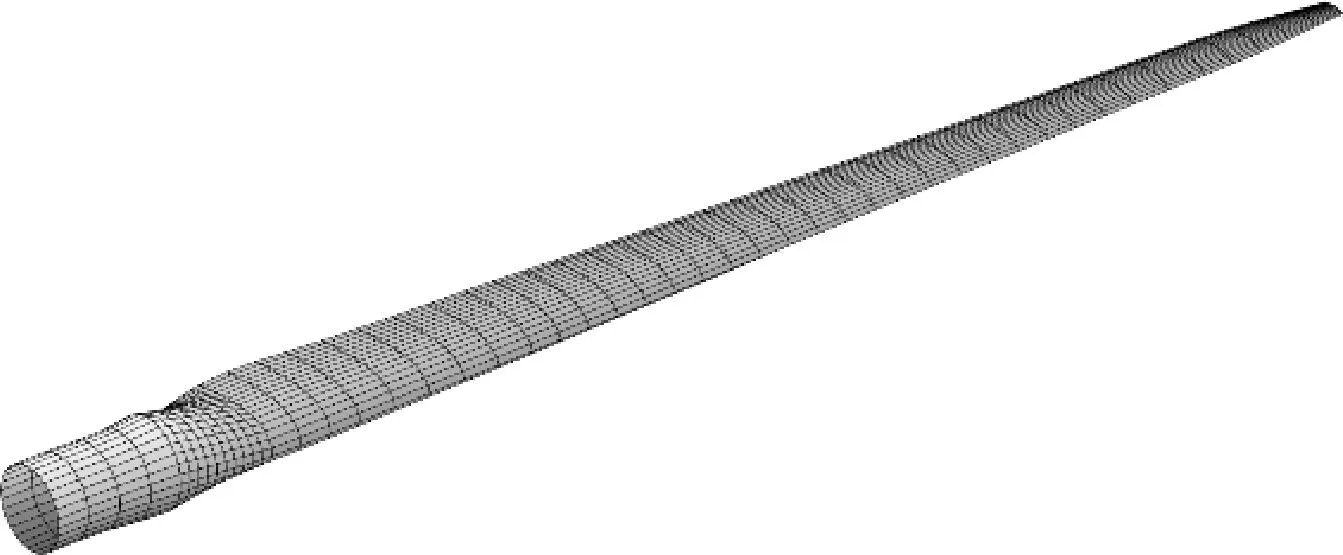
图4 叶片网格划分示意Fig. 4 Schematic diagram of blade meshing

假设风速为V0，风机的旋转速度为Ω，r表示计算点到风机旋转中心的距离，则叶片上的来流速度为[11]：

V∞=V0-Ω×r

(12)

由于影响系数Ck和Bk只和叶片的表面形状有关，因此不需要重复计算，但是在每个时间步都要重新计算来流速度V∞，根据式(8)更新表面的源强度大小。

针对非定常面元法，采用自由尾流模型，假定尾流是自由运动的，偶极子单元按照当地的流动速度进行移动，尾流上的偶极子分布[12]如图5所示。因此需要在每个时间步计算尾流处的诱导速度，从而确定尾流的几何形状，单元的位移增量为：

图5 尾流上的偶极子分布[12]Fig. 5 Doublet distribution on wake

(Δx,Δy,Δz)=(u,v,w)·Δt

(13)

同时在每个时刻脱落偶极子的强度不同，每经过一个时间步长，某一尾流面元上的偶极子向后一个面元处转移，每条尾涡带上第一个面元处的偶极子强度又等于叶片的定常尾流速度势。根据该理论可以获得叶片当前时刻步和下个时刻步的物理量变化关系[13]。图6给出了采用自由尾流模型，当浮式基础做纵摇运动时生成的尾流形状。

图6 自由尾流模型Fig. 6 Free wake model

每一时间步自动生成尾流面网格形式，确定了尾流面的形状后尾流影响系数也随之确定，利用Morino库塔条件来得到尾流面上的偶极子强度的初值，每条尾涡带上第一个偶极子单元的大小可以用未知量的形式来表示：

ΓW(j)=μI B,j-μ1,j

(14)

式中:j为不同的尾涡条带序号，IB为弦向网格数量(面元控制点编号从叶片下翼面后缘变到前缘再到上翼面后缘逐渐增加),μI B,j和μ1,j分别表示叶片后缘上、下表面偶极子强度。

2.2 等压库塔条件及黏性修正

采用Morino库塔条件只是得到计算的初值，但是对风机叶片这种三维翼型来说会产生较大的误差，还需要逐步迭代满足等压库塔条件，保证尾缘上下表面的压力相等。

Δp=pupper-plower=0

(15)

在每个面元上的压力系数为：

(16)

式中:v和p分别表示当地的速度和压力；vref和pref分别表示来流速度和压力；μ为叶片表面的速度势。

进一步对压力积分可以得到作用在风机上的推力和转矩，面积为ΔS的单个面元上沿nk方向上受到的力为：

(17)

由于面元法研究的是理想流体的势流问题，无法考虑流体的黏性产生的阻力,通过Prandtl-Schlichting表面摩擦阻力公式[14]对推力和转矩进行修正，该经验公式可以计入形状的影响，提高计算的准确度。叶片表面的摩擦阻力系数为：

(18)

式中:t表示叶片截面处的最大厚度，C表示叶片截面处翼型的弦长，Re表示雷诺数。推力和转矩黏性修正项的表达式分别为：

(19)

(20)

式中:Vm表示面元m上的表面切向速度，在叶片坐标系下的3个分量分别为(Vm,i,Vm,j,Vm,k)；Cf,m表示面元m上的摩擦阻力系数；NC和NR分别表示弦长方向和展长方向的网格划分数量；Z表示叶片数量；(x,y,z)代表面元m控制点的坐标；ΔSm表示面元m的面积。

3 浮式基础运动影响

当浮式基础产生6自由度运动时，不仅会改变作用在叶片上的风速方向，平台自身的运动速度也会对来流速度做出贡献，因此需要定义坐标转换关系来描述平台运动带来的影响。在描述过程中一共有3个坐标系，分别是：大地坐标系∑o1x1y1z1(坐标系1)，固定于平台并随平台转动的参考坐标系∑o2x2y2z2(坐标系2)，随风机叶片转动的叶片局部坐标系∑o3x3y3z3(坐标系3)。坐标系示意如图7所示。

图7 坐标系示意Fig. 7 Coordinate system diagram

根据坐标的转换关系，如浮式基础绕重心旋转(φ,θ,ψ)，坐标系1到坐标系2的转换矩阵形式则为：

(21)

坐标系1到坐标系2的转动角度即为横摇角θroll、纵摇角θpitch和艏摇角θyaw。将风速和平台的运动速度叠加后得到任一时刻叶片在坐标系2下的来流速度：

Vrel2(t)=f(θroll,θpitch,θyaw)vwind(t)+vP(t)+ωP×rp

(22)

其中，vwind为风速，vP和ωP分别为平台的平动和转动速度，rp为叶片面元到平台重心的矢量。

由于叶片在旋转过程中方位角的变化以及在安装时也会导致坐标系2和坐标系3之间存在角度的偏转，设2、3坐标系之间旋转的角度为(p,q,r)，经过坐标变换后，来流速度变为：

Vrel3(t)=f(p,q,r)Vrel2(t)+ωo×ro

(23)

其中，ωo表示叶片的旋转速度，ro表示叶片面元到旋转中心的矢量，将坐标系3下得到的速度代入式(8)中即可得到每一时刻步面元上的源强度大小。通过该过程将平台的运动和风速共同处理为非定常来流进行分析，建立了海上浮式风机的非定常面元法计算模型，为下一步的非定常气动性能分析奠定了基础。

4 剪切风和塔影效应

采用指数率来描述风速随高度的变化规律，考虑剪切风的影响时，风速的表达式为[15]：

(24)

其中，v(z)表示高度z位置的风速，vh表示轮毂处的风速，h表示轮毂高度，α表示风剪切指数，取值范围0.10～0.25之间。在每一时刻计算叶片旋转到不同位置处每个面元的高度z，然后将vshear赋予式(22)中的vwind，采用非定常面元法也能适用于求解复杂来流的情况。

由于塔架的存在会导致塔架后面的风速降低，采用潜流模型[16]来描述塔影效应，方位角为120°～240°之间的区域影响因子为：

(25)

其中，D表示面元所在高度的塔柱直径，x和y分别表示面元到塔柱中心的坐标分量。考虑塔影效应的情况下，将风速乘以影响因子赋予式(22)中的vwind。

浮式基础不运动时，叶片上风速大小和方向的变化只和方位角有关，不同叶片的功率之间只存在相位的差距[17]，因此多叶片风机不需要做重复的计算，对于三叶片风机，总的功率为；

P=P1+P2+P3=P1(θ)+P1(θ+120°)+P1(θ+240°)

(26)

5 计算程序及验证

根据非定常面元法的基本理论和计算模型，编写了海上浮式风机的气动载荷计算程序，计算流程图如图8所示。

图8 计算流程图Fig. 8 Flow diagram of calculation

该程序同样可以用来处理非定常流。在有限元软件中对叶片进行网格划分，根据上一时刻计算的诱导速度获取尾流面的位置信息，然后采用Newton-Rapshon方法进行迭代直到压力符合等压库塔条件，随后输出气动载荷，然后进入下一时间步的计算。程序对叶片的形状没有要求，不依赖已有翼型的气动参数，在后处理中可以显示整个叶片表面的压力场分布，并且迭代次数少，采用的算例在每个时间步迭代若干次后即可收敛，时间成本低。

为了验证面元法计算程序的合理性，给定定常风速，考虑叶片在安装时的锥角以及倾角，高风速下引进变桨策略，计入桨距角的影响。模拟了不同风速和转速下，风机的功率和推力，并和文献[10]中给出的NREL的设计值、文献[18]中的CFD计算结果以及文献[19]中的BEM/CFD结果进行对比，如图9所示。在引入黏性修正后，在额定工况下的输出功率为5.30 MW，和NREL的设计值(5.29 MW)十分接近。

图9表明，面元法计算趋势是正确的，功率计算值偏大推力计算值偏小，推力值和NREL设计值之间存在一些差别，但是和BEM理论的计算值较为接近，主要的原因是文中和文献[19]都还未考虑塔架的存在。

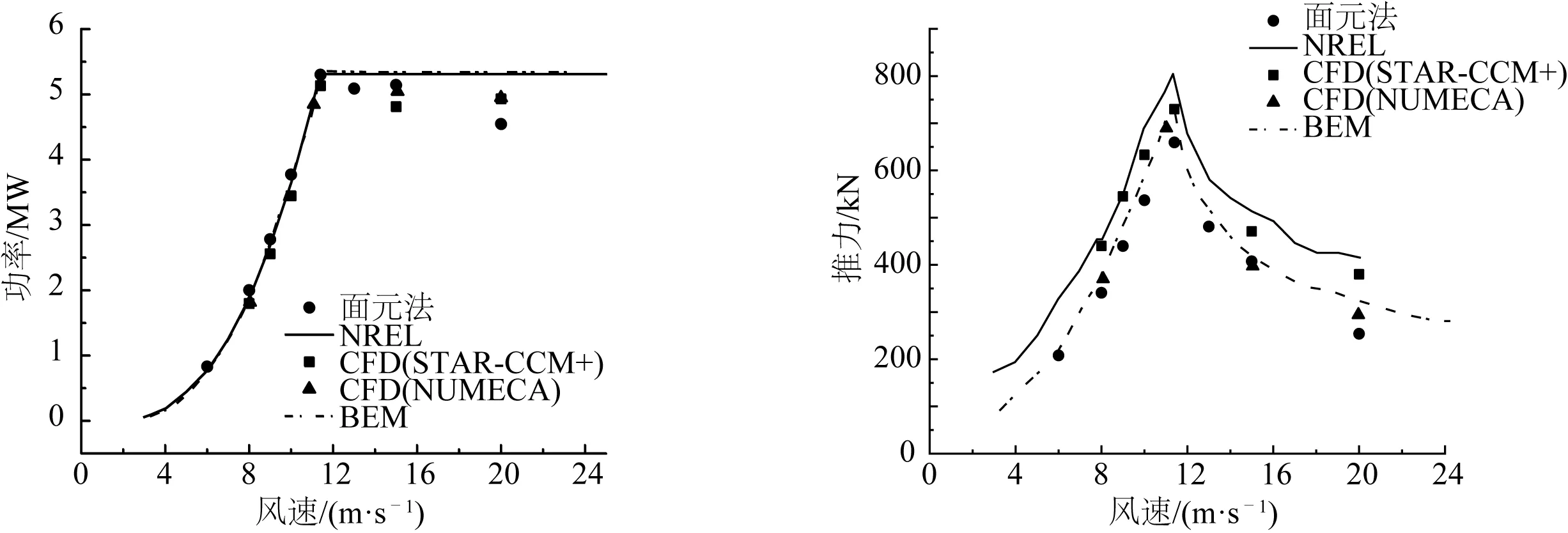
图9 功率和推力计算对比Fig. 9 Power and thrust calculation comparison diagram

图10给出了风速为9 m/s时，在0.45R、0.60R、0.80R、0.90R这几个截面处的压力系数分布。从图10中可以看出，在同一截面上，来流速度以一定的角度流过叶片，然后在前缘点发生分离，一部分沿下表面流动，另一部分绕过前缘点后再沿上表面流动，最后在尾流点汇集，在后缘点上下表面的压力系数值相等满足等压库塔条件。叶片压力系数较大的区域集中在叶片0.3R长度附近，并且在吸力面前缘会出现较大的峰值，因为吸力面前缘是叶片表面形状变化最剧烈的区域，面元法的速度是通过速度势的局部求导获得的，曲率过大会导致计算得到的速度也偏大，而在真实的流场中，速度过大时会在黏性作用下被很快的耗散掉[20]，这也是计算功率偏大的主要原因。

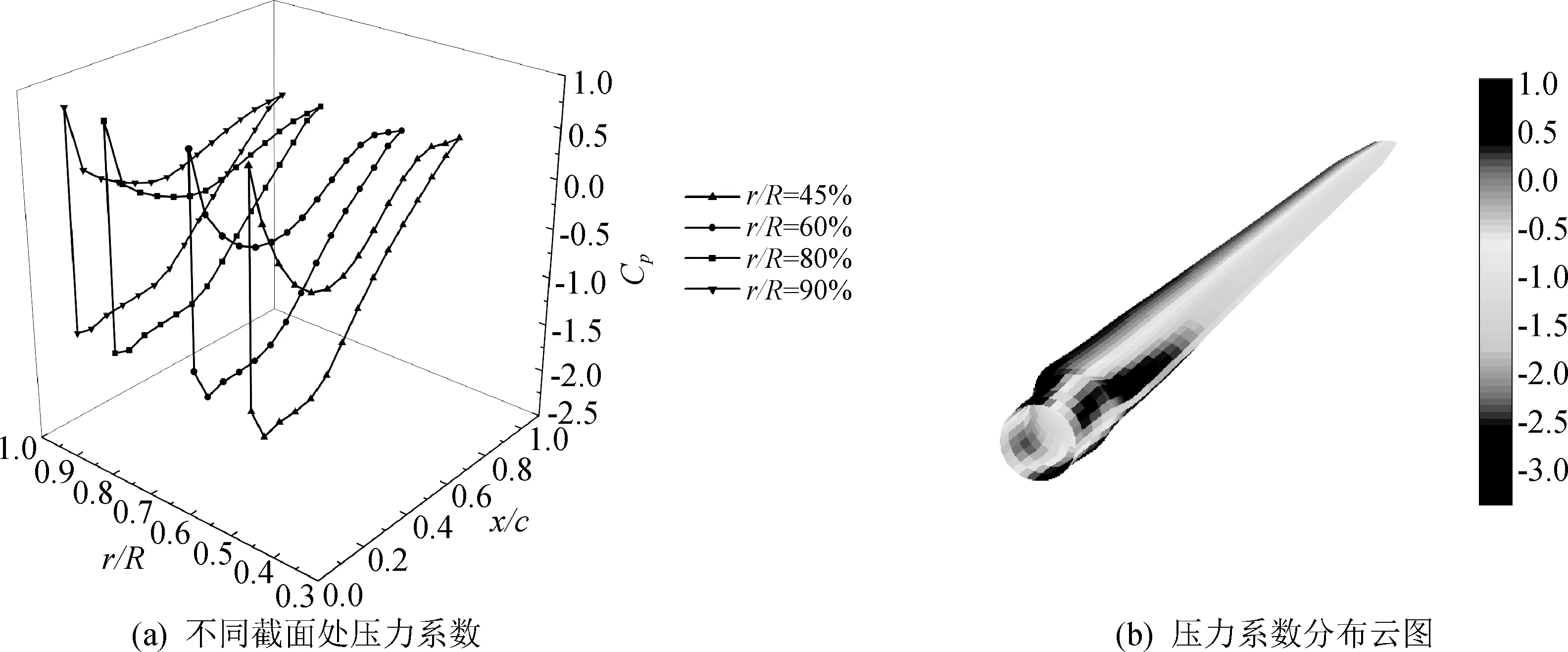
图10 不同截面处的压力系数和整个叶片上的压力系数分布云图Fig. 10 Pressure coefficient at different sections and cloud diagram of pressure coefficient distribution on the entire blade

6 风力机气动性能分析

6.1 剪切风和塔影效应对风力机功率的影响

对浮式风力机来说，随着方位角的变化，由于剪切风和塔影效应的影响，导致风速的大小和方向随时间产生周期性变化，使风机的输出功率产生波动。

图11给出了在额定风速11.4 m/s下单个叶片的输出功率，从图中可以看出剪切风会导致功率出现简谐波动，波动的范围在1.42～2.01 MW之间，而塔影效应会导致在方位角达到180°时降到最低值1.55 MW，两者联合作用时，下降的幅度更大，最小的功率值为1.26 MW。相比剪切风，塔影效应对风机输出功率的稳定性影响更大，当风机转到塔架位置时会导致功率突然降低随后又突然上升，呈V字形变化，而总的输出频率是风机旋转频率的三倍(见图11)。图12总结了几种不同模型下总功率的变化趋势。以上分析表明：剪切风的影响机理是使功率产生简谐波动并且降低输出功率，塔影效应产生的主要影响是当叶片旋转到塔柱位置时产生功率的骤降，两者共同作用下，波动幅值比塔影效应单独作用时要小，剪切风能适当降低塔影效应带来的不稳定波动，气动载荷出现风轮旋转的3P频率成分。从结果来看非定常面元法能很好地模拟风机的非定常效应，反映入流风速变化对气动力带来的影响。

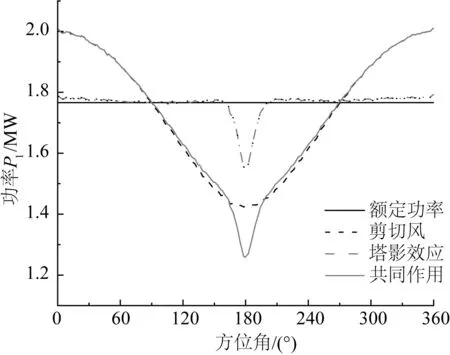
图11 剪切风和塔影效应对功率的影响Fig. 11 Effect of shear wind and tower shadow on power

图12 总功率随方位角的变化Fig.12 Variation of total power with azimuth angle

6.2 浮式基础运动对气动载荷的影响

为了研究浮式基础运动对风机气动载荷的影响，且为了避免变桨工况，设定风机在风速9 m/s下运行，转速为10.33 r/min，计算时间步长为0.1 s。浮式基础纵荡速度和风速在一个方向上，直接影响来流风速的大小，而纵摇和艏摇会改变风速的方向，使风机处于偏航状态，因此选取了对风机气动性能影响显著的3个自由度的运动：纵荡、纵摇和艏摇，将浮式基础这3个自由度的运动简化为正弦运动，运动周期和幅值见表1，数值的选取参考了真实海况下浮式基础的运动[21-23]。当叶片旋转到不同的角度时，由于浮式基础的转动角度和提供的附加速度大小都不相同，不能简单的转换相位进行叠加，采用非定常面元法的计算思路是在计算不同的叶片时改变初始方位角，具体体现在式(23)中的角度p上，从而导致转换矩阵也各不相同，计算得到不同叶片上的气动载荷随后进行叠加，最后得到总的功率和推力随时间变化的结果，如图13～17所示。

表1 平台运动工况

图13 浮式基础纵荡对总功率和推力的影响Fig. 13 The influence of surge on floating foundation on total power and thrust

以上计算表明：浮式基础的纵荡和纵摇对风力机气动载荷的影响较大，当浮式基础在这两个自由度做正弦运动时，风力机总功率和推力的变化周期和浮式基础的运动周期一致。浮式基础发生艏摇运动时，风力机的总功率变化周期和叶片的旋转周期一致，变化较为平稳，但是单个叶片上气动载荷的波动较为复杂，每个叶片上气动载荷的变化周期等于艏摇运动的周期，同时每个叶片之间不止存在相位角的差距，气动载荷的幅值和变化趋势都不相同。

此外，计算结果还表明，浮式基础纵摇和纵荡对叶片气动载荷的波动影响最大，不考虑平台运动时算得的功率值为2.78 MW，而纵摇会使得风机功率的范围从1.15 MW变化到4.84 MW。因此，浮式基础纵摇显著影响风机输出功率的稳定性，实际中应对其加以必要的控制。在浮式基础纵荡的影响下，文中算例中，使得风机功率的变化范围从2.04 MW变化到3.43 MW，虽然纵荡运动不会影响来流风速的方向，但是会提供额外的附加速度，当平台纵荡运动速度过大时会显著改变风轮输出功率的波动范围；浮式基础艏摇对风机总功率波动范围的影响非常小，风机功率的波动范围在0.05 MW以内。

图14 浮式基础纵摇时的总功率和推力Fig. 14 Total power and thrust of pitch

图15 浮式基础艏摇时总功率和推力Fig.15 Total power and thrust of yaw

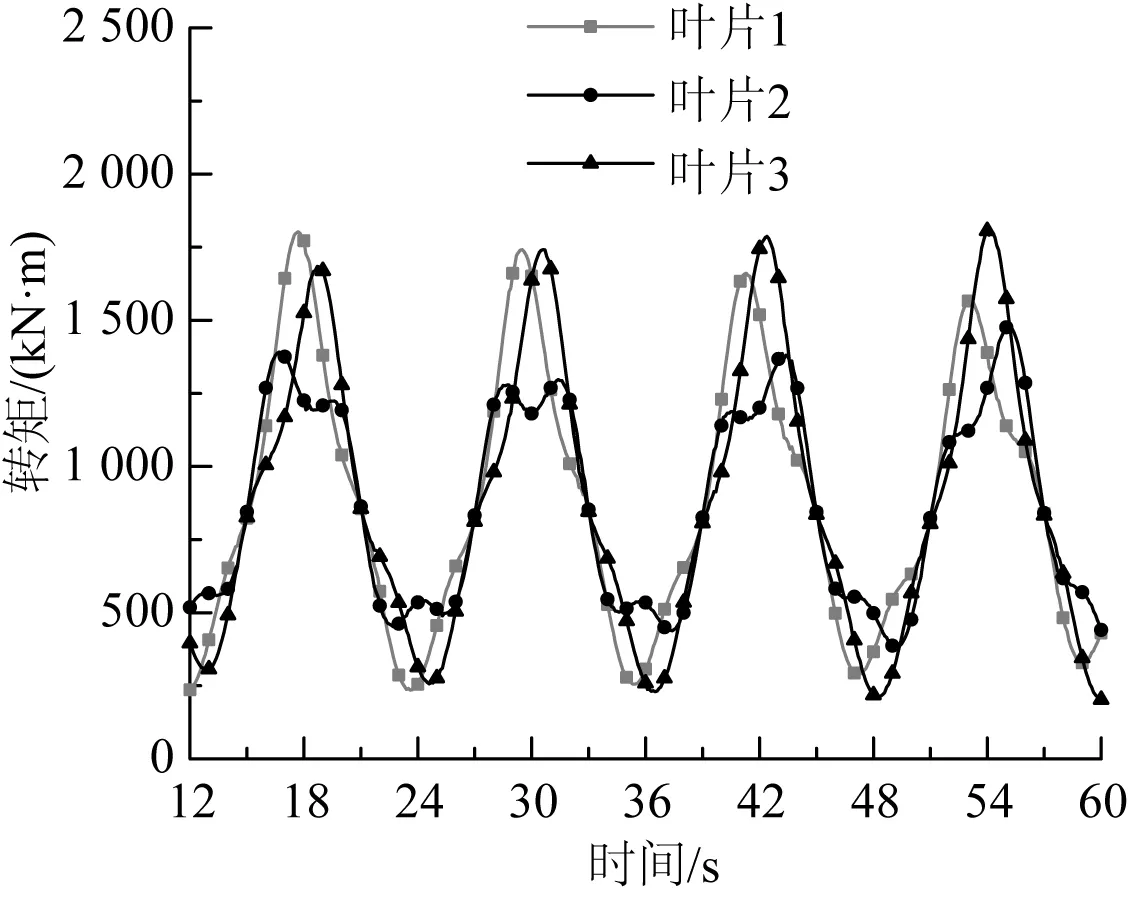
图16 浮式基础纵摇时各个叶片上的转矩Fig. 16 Moment on each blade of pitch

图17 浮式基础艏摇时各个叶片上的转矩Fig. 17 Moment on each blade of yaw

根据以上分析可知，适当的浮式基础运动会提高风机的输出功率，但是会导致风机输出功率的不稳定，而叶片之间相位角的差距能适当弥补这种波动带来的不稳定性。

图18进一步给出了计算稳定后，不同时刻风机叶片表面的压力场分布云图。可以看出，在0.5R～0.9R长度范围内，风机叶片吸力面前缘部分压力最大，压力的最大绝对值先变大再减小；压力面上的压力随时间变化不明显，同时经过非线性迭代后，在后缘上下表面的压力大小相同，并且在该区域范围内压力过渡平滑，说明满足非定常等压库塔条件。

7 结 语

基于三维速度势的非定常面元法，开发了浮式水平轴风力机的气动载荷计算程序，以NREL 5 MW风机为例，分析了剪切风、塔影效应以及浮式基础运动对风机气动载荷的影响。研究结论如下：

1) 研究了剪切风和塔影效应对风机气动性能的影响。结果表明，考虑剪切风和塔影效应时，单个叶片上气动载荷的变化频率等于风机的转动频率，塔影效应对风机功率的稳定性影响显著，风机整体在方位角位于60°、180°和300°时会发生输出功率的突然下降。

2) 分析了浮式基础纵荡、纵摇和艏摇运动对风力机气动性能的影响。结果表明，总的输出功率和推力的变化周期以浮式基础运动的周期为主。浮式基础纵荡和纵摇对风机整体功率波动幅值的影响很大，不利于海上风机的稳定运行；而对单个叶片而言，其气动载荷对浮式基础的艏摇会更加敏感。

3) 分析了风机叶片压力分布特征。结果表明，叶片压力系数较大的区域集中在叶片0.3R长度附近，压力较大且变化比较剧烈的区域在0.5R～0.9R展长处的叶片前缘附近，在风机叶片结构设计时应对该区域的强度给与额外的关注。