漂浮式风力机非定常气动特性分析
林 易 ,李 晔 ,段 磊
(上海交通大学 a. 海洋工程国家重点实验室;b. 高新船舶与深海开发装备协同创新中心;c. 船舶海洋与建筑工程学院,上海 200240)
0 引 言
叶素动量(Blade Element Momentum, BEM)理论、涡方法和计算流体动力学(Computational Fluid Dynamics, CFD)方法是当前主流的风力机气动力学计算方法,其中涡方法相对于CFD方法计算量小,相对于BEM方法计算精确度高,目前已广泛应用于风力机气动性能预测和尾流场模拟中。对于涡方法而言,在采用预定涡方法和刚性涡方法时都需提前建立尾迹中涡线轨迹的描述函数,而在采用自由涡方法(Free Vortex Method, FVM)时允许涡线随当地入流并受涡线间诱导的影响发生自由移动,因此FVM能更准确地计算出风力机的气动性能和尾迹场[1]。
近年来,相关学者采用FVM对风力机的气动性能进行了深入的研究和运用[2-3]。为准确模拟漂浮式风力机的瞬时运动状态,部分学者采用时间步进 FVM 在时间域内对风力机尾迹涡线进行迭代求解。BHAGAWAT等[4]通过对空间离散运用五点差分格式,对时间步离散运用三点差分格式,迭代求解风力机的自由涡尾迹场。GUPTA[5]对风力机自由涡尾迹方法中的算法问题进行分析,从准确性、稳定性和收敛性等3方面探讨不同计算方法之间的区别。许波峰[6]提出一种求解风力机气动性能的时间步进差分格式,并发展一种自适应松弛因子方法,用以提高数值迭代的稳定性和收敛速度。这些研究重点考虑风力机气动力学的计算方法,针对漂浮式风力机的气动特性计算问题,通过预设平台运动计算水动力学的影响。
相比固定式风力机,漂浮式风力机的支撑平台在风、浪、流等环境载荷作用下的不规则运动会加剧其叶轮的非定常气动特性。现有的算法能较为精确地模拟固定式风力机的动态特性,但难以对漂浮式风力机的水动-气动耦合数值进行模拟,同时缺乏自诱导对海上风力机动态特性影响的讨论和验证。在采用FVM求解风力机的气动特性时,远尾迹的单叶尖涡模型无法准确反映风力机的尾流结构特征。本文通过引入约化频率的概念,研究海上风力机在不同运行状态下的非定常特性及其成因,阐述漂浮式风力机相比固定式风力机具有更强的气动复杂性。同时,应用全自由涡尾迹模型,基于时间步进FVM,考虑不同的数值计算方法,分别计算固定式风力机和漂浮式风力机的气动性能,并对二者进行对比分析,讨论风力机的运行状态及算法选择对计算精度和尾迹场稳定性的影响。此外,分析自诱导对风力机动态输出的影响。
1 漂浮式风力机非定常气动载荷
当风力机处在复杂的环境流场之中时,其叶片的气动性能具有非定常特性。当攻角较小时,叶片局部的流动形式表现为全附着涡,可基于准定常情况进行分析;当攻角较大时,叶片局部会产生随时间变化的流动分离现象,引发动态失速等非定常效应,随之改变翼型处流体变化的振幅和频率。对于漂浮式风力机而言,其支撑平台的运动可能会导致其叶轮在某些时刻进入自身的尾迹场,进而产生附加的瞬时载荷。为准确探讨海上风力机非定常气动特性的复杂性,进而说明适用的数值模拟方法,需对这些影响进行全面的研究。
通常情况下,风力机在运行过程中持续地从流场中吸收能量。对于漂浮式风力机而言,其支撑平台的纵摇运动使风力机沿平衡位置发生振荡。在某些时刻,风力机会进入其自身尾流场,其功率随之下降。在极端情况下,叶轮处在螺旋桨运行状态,向外做功。漂浮式风力机受支撑平台运动的影响产生的非定常气动特性使其有别于固定式风力机,需进行特殊的分析与校核。部分学者采用约化频率对叶片的非定常气动特性进行定量分析。通过对Navier-Stokes方程进行无因次化,可将无因次叶片受力[7]表示为
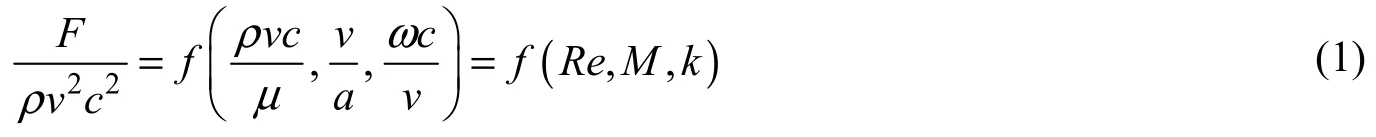

式(1)中:v为当地速度;ω为桨叶运动的角频率;c为叶片的弦长;k为约化频率。k表示叶片翼型的非定常气动特性,满足LOEWY[8]对翼型在不同流动状态下的约化频率k进行范围界定:当0.05k≤时,局部流动可看作定常态;当k>0.05时,局部流动看作非定常态。
本文以美国国家可再生能源实验室(National Renewable Energy Laboratory, NREL)的5MW offshore Baseline Wind Turbine[9]为对象进行讨论。约化频率验证工况见表1。

表1 约化频率验证工况
表1中各工况对应的漂浮式风力机约化频率见图1,其中:叶片转动影响即为转机带动叶片转动产生的对风力机约化频率的贡献值;波浪影响即为波浪对风力机约化频率的贡献值。由图1可知:在靠近叶片处,约化频率较大;在漂浮式风力机运动过程中,波浪对其影响不可忽略,与固定式风力机相比,漂浮式风力机的气动特性具有较强的非定常效应,且桨叶上具有较强非定常气动效应的区域较大,此时传统的BEM方法不再适用。因此,应考虑采用能更准确地描述风力机非定常气动特性的FVM等方法。
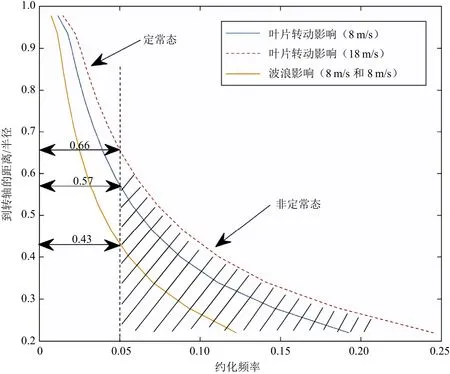
图1 不同工况下漂浮式风力机约化频率
2 漂浮式风力机数值计算方法
本文采用基于全自由涡的时间步进方法开展风力机数值模拟和非定常气动特性研究。图2为FVM示意,其中:叶片模拟采用升力线模型,在叶片1/4处布置一根相同展长的边界涡元(Bound Filament);尾迹场模拟采用涡格模型,可表示为脱落涡(Shed Filament)和尾随涡(Trailed Filament),随时间迭代可求得尾迹场轨迹;计算算法分别采用前进欧拉法、二阶Adams-Bashforth和四阶Adams-Bashforth法。
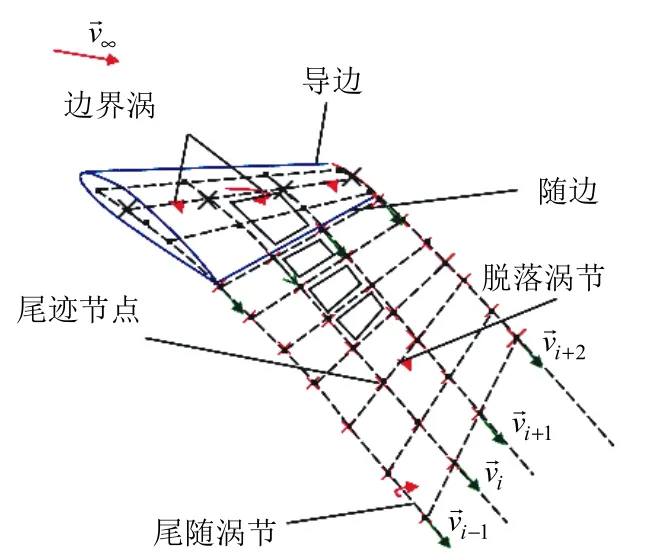
图2 FVM示意
对于风力机的尾迹场而言,可根据亥姆霍次定理得到控制点的控制方程为

式(3)中:r为涡节上的控制点位置向量;v为控制点的当地速度。将式(3)化为偏微分方程,可得

式(4)中:ψ和ζ分别为方位角和尾龄角。通过对式(3)左侧时间和空间域进行离散和数值求解,将式(3)转化为离散形式,有

式(5)中:Dψ和Dζ分别为方位角和尾龄角的一阶差分。式(5)右侧速度项包含自由流速、外部扰动速度和尾迹场诱导速度,可表示为

式(6)中:v∞为自由流速;vex为外部扰动速度;vind为尾迹场诱导速度。vind具有高度非线性,可通过Biot-Savart定律进行计算。
运用不同算法对式(5)进行求解,显式Euler法可表示为

二阶Adams-Bashforth和四阶Adams-Bashforth欧拉法分别表示为
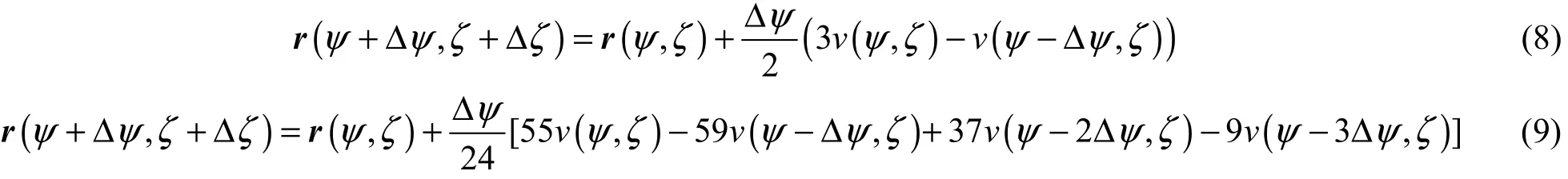
分别利用以上算法对固定式风力机和漂浮式风力机进行相应的数值模拟。对于漂浮式风力机而言,本文的水动力计算基于经典势流理论,将水动力学问题分解为绕射、辐射和静水问题,根据文献[10]所列特性和参数进行改进。同时,为突出海上风力机在复杂流场中的动态特性,结合参考模型的对称性特征并假设艏摇位移较小,仅考虑支撑平台的纵荡、垂荡和纵摇影响,对支撑平台、塔架和机舱复合结构及桨叶提出刚体假设,即忽略桨叶与轮毂、轮毂与转机和塔架与平台等结构之间的连接自由度,仅考虑桨叶随轮毂旋转的自由度。
3 结果与分析
3.1 工况设置
选择NREL的5MW Baseline Wind Turbine[9]作为计算模型,并针对固定式平台和漂浮式平台对风力机的气动性能进行数值模拟。表2为主要的环境条件和参数,其中漂浮式风力机平台选用NREL OC3 Hywind[10]平台。

表2 主要的环境条件和参数
对固定式风力机和漂浮式风力机进行数值模拟,采用的算法为前进 Euler法、二阶 Adams-Bashforth方法和四阶Adams-Bashforth方法,其中:前进Euler法具有一阶稳定性;二阶Adams-Bashforth方法和四阶Adams-Bashforth方法具有二阶稳定性和三阶稳定性。
3.2 算法验证
针对本文设计的自由涡求解程序对固定式风力机进行计算。图3为前进Euler法下固定式风力机与FAST软件的功率比较,运用全自由涡时间步进方法,计算时间为300s,风速为18m/s,转速为12.1r/min,桨距角为15°。比较发现两者的计算结果基本吻合,说明本文采用的时间步进FVM具有一定的精确性。
3.3 固定式风力机计算结果
图4为基于不同算法的固定式风力机功率比较。由图4可知,不同算法下的固定式风力机功率值相近,说明算法选择对固定式风力机输出功率的影响很小。图5~图10为不同算法下的海上风力机尾迹几何形状,以风轮轴线为主轴,建立笛卡尔坐标系,图中坐标为实尺度与风力机直径的比值,皆为无因次参量。图6、图8和图10为不同算法下固定式风力机尾迹俯视图。通过比较图6、图8和图10可知:风力机尾迹在距离风力机约3倍直径处出现数值不稳定现象,且算法对风力机尾迹几何的数值稳定性有一定的影响;在同等时间步下,相比二阶Adams-Bashforth法和四阶Adams-Bashforth法,前进Euler法下的风力机尾迹较早出现数值不稳定现象,其所得情况与文献[4]的判断结果一致。
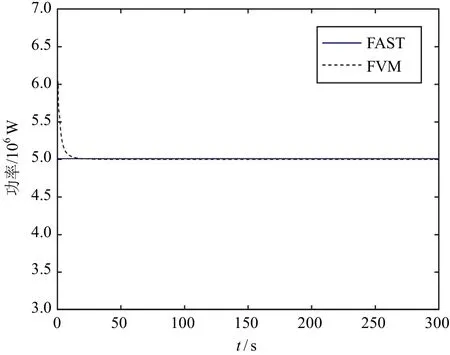
图3 前进Euler法下固定式风力机与FAST软件功率比较
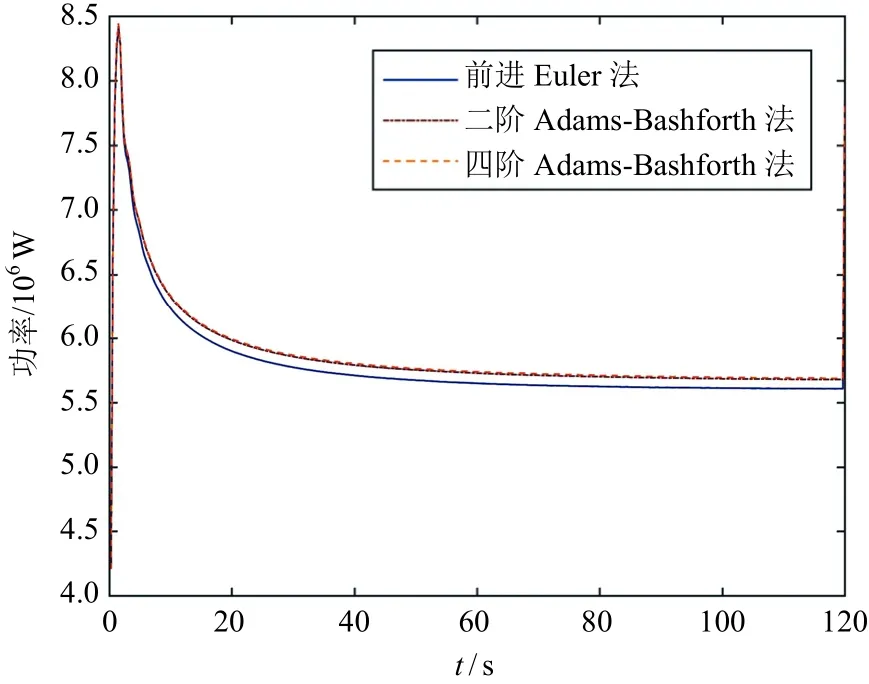
图4 基于同算法的固定式风力机功率比较

图5 前进Euler法下固定式风力机尾迹
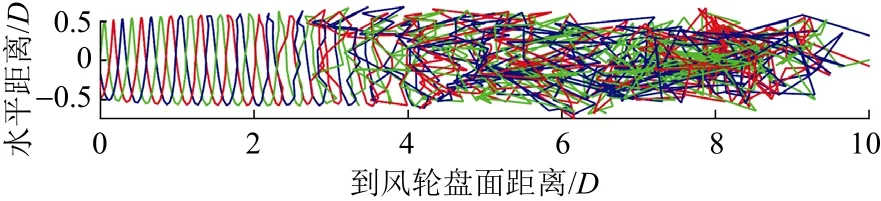
图6 前进Euler法下固定式风力机尾迹俯视图
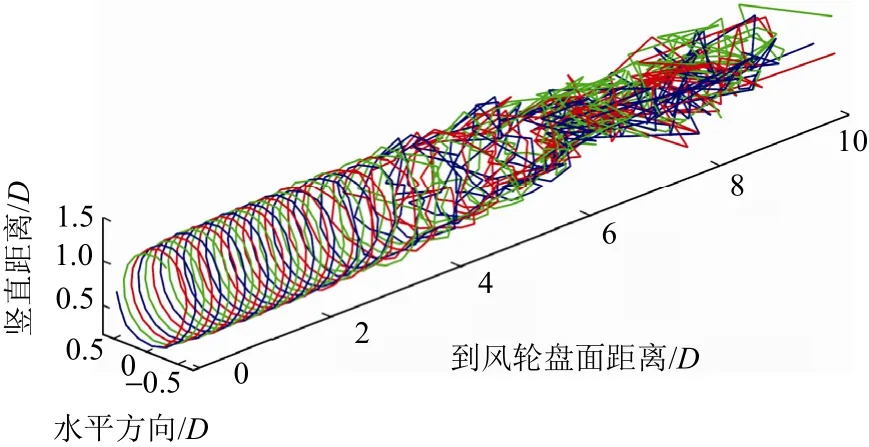
图7 二阶Adams-Bashforth法下固定式风力机尾迹

图8 二阶Adams-Bashforth法下固定式风力机尾迹俯视图
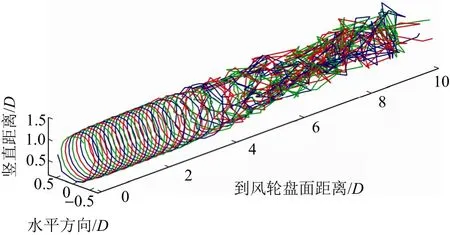
图9 四阶Adams-Bashforth法下固定式风力机尾迹

图10 四阶Adams-Bashforth法下固定式风力机尾迹俯视图
3.4 漂浮式风力机计算结果
图11为不同算法下漂浮式风力机功率比较。由图11可知,不同算法下的漂浮式风力机功率值相近,说明算法选择对漂浮式风力机输出功率的影响较小。图12~图14为漂浮式风力机尾迹的几何形状。由图12~图14可知,漂浮式风力机尾迹相比固定式风力机在几何上存在更多的不均匀性,说明漂浮式风力机支撑平台的运动会影响其轨迹形状。
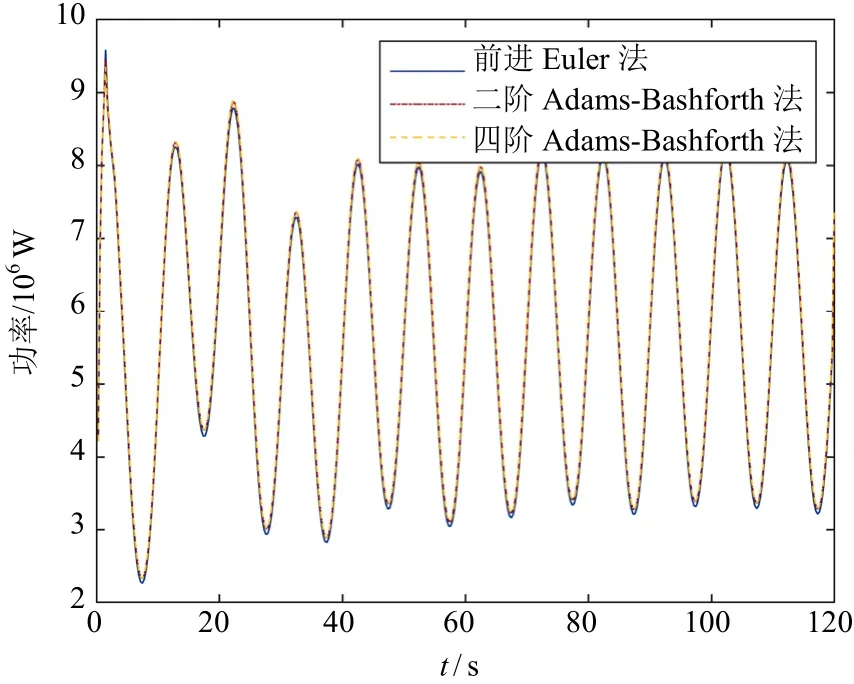
图11 不同算法下漂浮式风力机功率比较

图12 前进Euler法下漂浮式风力机尾迹
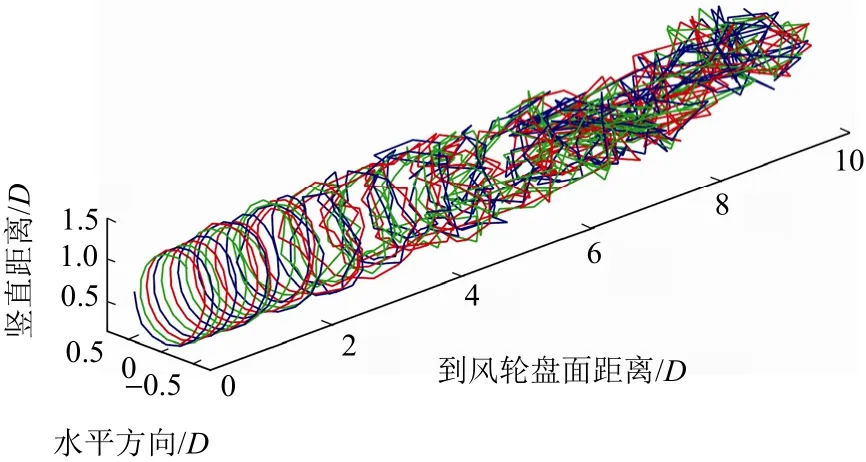
图13 二阶Adams-Bashforth法下漂浮式风力机尾迹
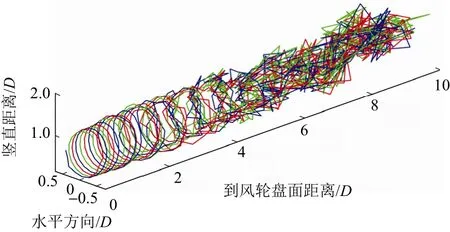
图14 四阶Adams-Bashforth法下漂浮式风力机尾迹
3.5 FVM诱导速度影响
式(6)右侧包含自由流速、外部扰动速度和自诱导速度,其中自诱导速度为所有涡线在叶片边界元位置处的诱导速度。图15为无自诱导时的风力机尾迹,由于此处只考虑自由流速的影响,该尾迹显示出均匀性。
图16~图19为有无自诱导速度时的风力机功率和推力比较。对于固定式风力机而言,无自诱导速度时的功率相对误差为11.6%,推力相对误差为5.4%;对于漂浮式风力机而言,无自诱导速度时的功率相对误差为10.8%,推力相对误差为5.0%。由该对比结果可知:对于2种风力机而言,自诱导速度对其动态输出的结果具有较大的影响,且不考虑自诱导影响时结果偏大;由于风力机产生的尾流与自由流速方向相反,因此该结果与正常情况相符。
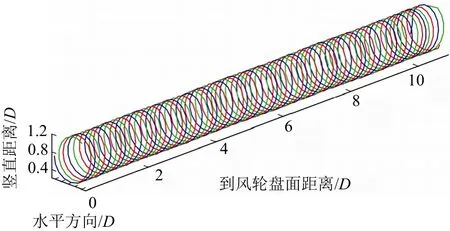
图15 无自诱导时的风力机尾迹
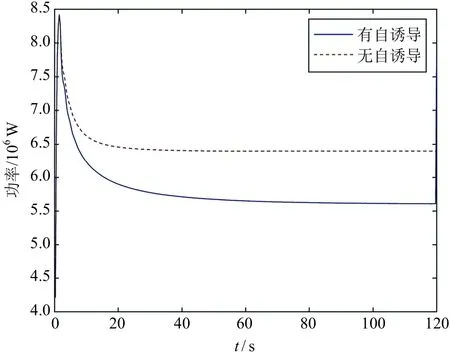
图16 固定式风力机功率比较
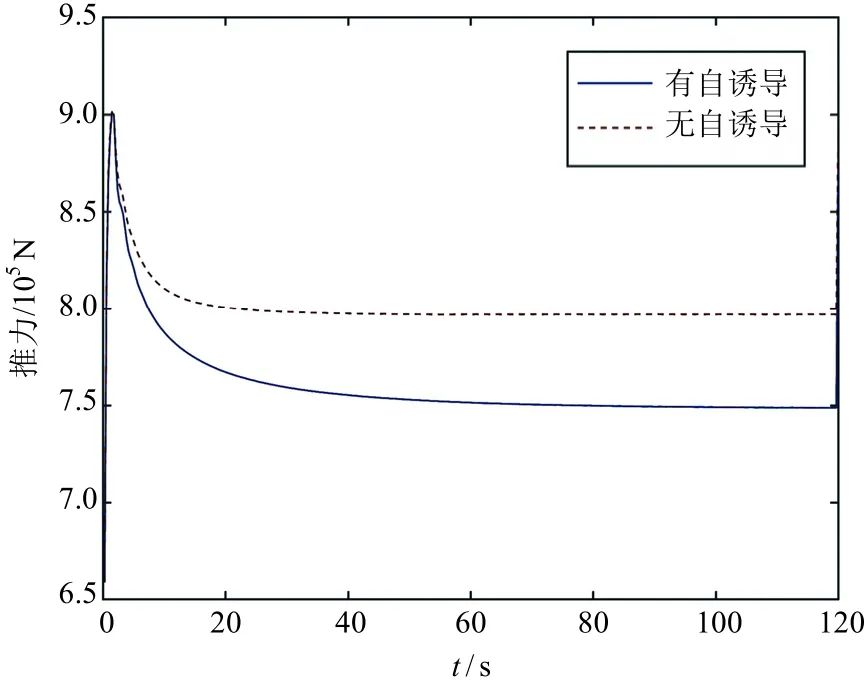
图17 固定式风力机推力比较
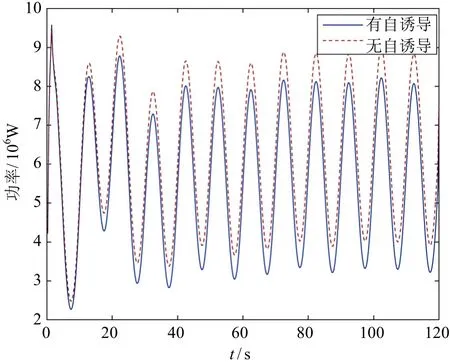
图18 漂浮式风力机功率比较
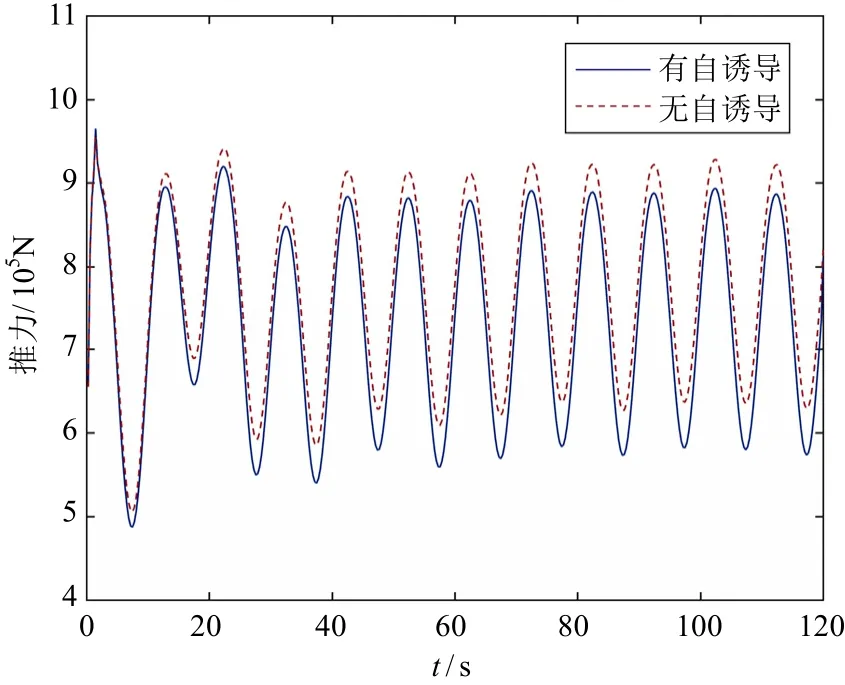
图19 漂浮式风力机推力比较
4 结 语
通过以上分析,可得到以下结论:
1) 对于风力机而言,漂浮式风力机因平台的运动相比固定式风力机存在更强的非定常气动特性,叶片流动状态更复杂,此时传统的基于动量守恒原理的方法不再适用。通过对风力机旋翼问题中的约化频率进行研究可知,风力机桨叶气动非定常性的因素来源主要包括叶片转动影响和波浪影响,其中波浪影响不可忽略。
2) 不同算法对漂浮式风力机的动态输出计算结果的影响较小,对尾迹稳定性的影响较大。前进Euler法由于只具备一阶稳定性,相比二阶Adams-Bashforth方法和四阶Adams-Bashforth方法,其尾迹更早出现数值不稳定特征。
3) 自诱导速度对风力机动态输出特性有较大的影响。

