用于振荡水柱波能系统的径流式空气透平数值模拟研究
杨 鑫,刘 臻,张晓霞
(中国海洋大学 工程学院,山东 青岛 266100)
随着社会的发展,人类活动对环境的影响、能源安全和可持续发展等矛盾一直是世界各地许多国家和组织议程的首要问题。欧盟、中国、美国等[1-6]全球能源市场的主要参与者更是越来越重视这些问题,他们所制定的政策与发展方针正在推动以清洁的可再生能源为主导的能源转型进程,使可再生能源可以作为化石燃料的可靠替代品。海洋可再生能源是几乎未被开发的清洁能源,具有极高的可用性,其估计储量大约为151 300 TWh/A,其量级与世界对一次能源的需求量相当[7]。
在许多国家,尤其是欧洲和亚洲国家,波浪能被认为是一种丰富而有前途的可再生能源[8-9]。在各种各样的波浪能系统转换装置中,振荡水柱波能转换系统被认为是用于捕获波浪能的最常用装置,因为其可与沉箱防波堤相结合,且除透平外无其他可活动机械部件,因此安装成本低且维护方便。其中可以转化为可用能量的大小,在很大程度上取决于气室内部和空气透平内部的流动特性,这些流动用于将气动能转换为机械能。作为振荡水柱波能转换系统的二级能量转换装置,空气透平主要包括轴流式、径流式两种类别,其中径流式空气透平的径向配置能明显降低其轴向推力,且具有较低的制造成本和较高的扭矩输出[10],因此关于径流式透平的研究也得到越来越多的重视。Setoguchi等[11]用试验的方式研究了导流叶片角度对径流式透平特性的影响,并建议将25°作为内、外侧导流叶片的最佳选择;Pereiras等[12]分析了转子尖端间隙、内侧导流叶片和外侧导流叶片对该透平性能的影响,观察到叶尖间隙效应在透平内部流速较高的区域更为明显;Elatife等[13]对径流式透平进行了进一步的优化,成功的使用试验设计(DOE)方法分析了10个几何参数对透平性能的影响,研究发现转子叶片对透平效率的影响最大,尤其是叶片安装角,当交错角为4°时透平在吸气与呼气阶段均能保持较高的效率,其效率提高了19%;Ansarifard等[14]利用9个设计变量控制转子的形状及调整气流向内流动方向,通过使用非对称的叶片,发现优化的转子可实现较高的输出功率,同时优化了下游部分,以便与优化的流入转子有效匹配,并使用4个参数控制下游部分的形状,结果表明优化后的透平在吸气模式下的稳态峰值效率可达81%;Falcao等[15-16]和Gato等[17]介绍了一种新型的径流式自整流透平,该透平结构较为复杂,但是峰值效率却能达到80%以上。其他大多数研究也都集中在透平的转子及导流叶片。由此可见,转子及导流叶片对透平性能影响极其重大。
目前对径流式空气透平的研究均是对转子叶片及导流叶片结构和安装角度进行探索,还没有对叶片数量的影响进行研究。针对这一问题,将展开不同转子叶片稠度对透平性能影响的研究。
1 研究内容
1.1 研究方法
在对透平运行特性的研究中,其动力输入条件及工作性能评价均包含定常与非定常两个概念。若入射气流的大小、方向均不随时间发生变化,则称为定常气流条件,反之称为非定常气流条件;若透平的扭矩、压强、转速等输出物理量均不随时间发生变化,则称为定常工作状态,此时透平展现出定常工作性能,反之称为非定常工作状态,此时透平展现出非定常工作性能。虽然在实际海况下流经透平的气流是不规则、非定常的,但是将气流条件简化为定常气流是对实际问题的合理简化,有助于揭示透平的基本工作原理并优化其结构形式,是一种研究透平的高效手段。
通过应用机械设计软件Solidworks15.0及商业计算流体力学(CFD)软件Fluent实现数值模拟计算。径流式空气透平结构复杂,因此利用专业机械设计软件Solidworks15.0进行几何建模;随后采用ICEM实现透平网格划分,为保证计算精度及减少计算时长,在全流域采用结构化网格;最后利用Fluent16.0进行数值计算。Fluent基于有限体积法求解Navier-Stokes方程,流动模型通过使用分离的求解器来求解不可压缩的流体守恒方程,其中扩散项采用中心差分格式进行离散,对流项采用二阶精度迎风格式进行离散,压力—速度耦合通过SIMPLE算法执行。在湍流模型的选择时,参考已有数值研究经验[18],使用realizable k-ε湍流模型与标准壁函数。相比于非定常数值计算,定常数值计算能够在保证结果可靠性的同时,大大缩短计算运行时间,充分提高研究效率。因此,所有数值计算均在定常条件下进行。
1.2 几何模型
文中主要研究用于振荡水柱波能装置的径流式空气透平,径流式透平的轴向进/出口连接到气室出口,如图1所示,其中转子与内、外侧导流叶片均等距分布。该透平主要参数如表1~3所示。
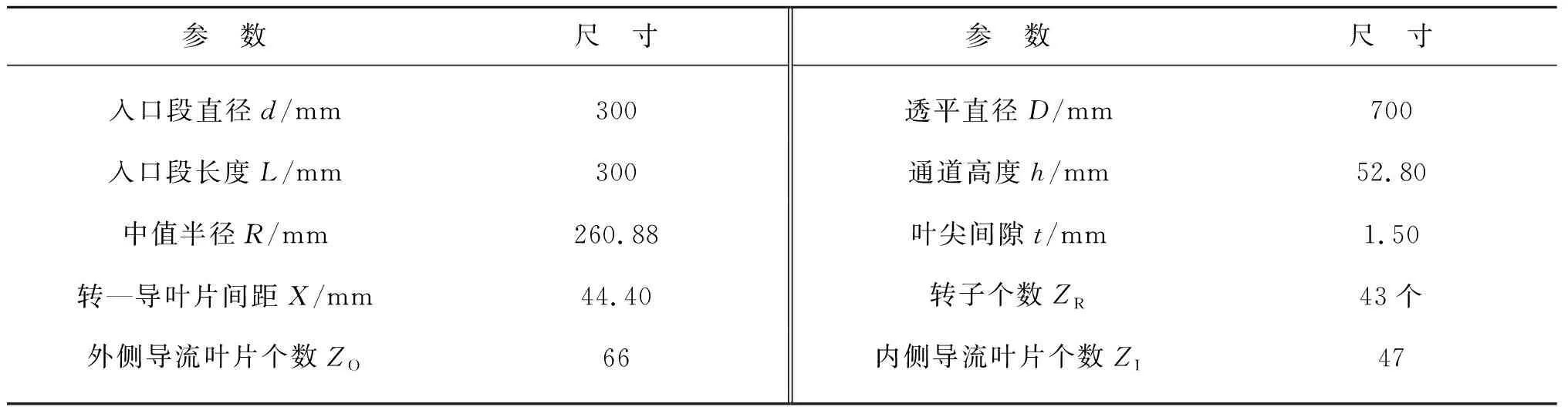
表1 透平规格Tab. 1 Specifications of radial turbine

图1 径流式透平结构示意Fig. 1 Schematic of radial turbine
转子叶片是透平直接提取能量的结构,除转子叶片结构外,合理配置转子叶片个数与弦长也是保证透平正常运行的关键因素,目前,常用稠度来描述透平转子叶片个数,稠度σ是表征透平叶片个数的无量纲数,其与叶片个数ZR、叶片弦长lR、透平中值半径R的关系为:
(1)
此次研究将选用5种不同的转子叶片稠度来讨论其对透平工作性能的影响,在实物装置转子稠度1.70的上下进行稠度选择,稠度分别为σ=1.38、1.70、2.02、2.34、2.65,其对应的转子叶片个数分别为:ZR=35、43、51、59、67。

表2 转子叶片规格Tab. 2 Specifications of rotor

表3 导流叶片规格Tab. 3 Specifications of guide vane
1.3 网格划分
研究借助ICEM实现三维结构化网格的构建,具体网格划分如图2所示。研究只针对振荡水柱波能系统的二级能量转换装置空气透平,因此忽略气室对透平的影响,并对透平进行合理简化。

图2 网格示意Fig. 2 Schematic of mesh
径流式空气透平中仅转子旋转,其内、外侧导流叶片均不旋转,因此需将整个计算域划分为几个不同区域:旋转的转子叶片区域,静止的内、外侧导流叶片区域以及入口区域。其中,不同子区域之间的数据传递通过Interface实现。透平转子区域可相对内、外侧导流叶片旋转以模拟转子定转速运动。此外,在不同区域的交界面、转子叶片及导流叶片处的网格分布较为紧密,这是由于叶片周围的流场较为复杂,需要加密网格保证计算精度。最后利用多参考系模型实现透平定转速运动的模拟。
2 研究结果
透平运行特性的计算结果用扭矩系数CT、输入系数CA和效率η表示,它们均与流量系数φ相关,其定义如下[11]:

(2)
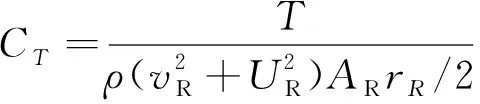
(3)

(4)
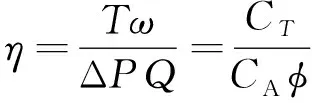
(5)
式中:ΔP为透平入口与出口两端的压降;T为透平输出扭矩、Q为气流流量;AR表示中值半径处的截面面积;vR表示中值半径处的径向流速,UR表示转子圆周速度。AR、vR与UR可分别定义为:
AR=2πrRh
(6)
(7)
UR=ωrR
(8)
2.1 模型验证
由于计算将在全流域进行,并非采用周期边界条件,因此模型网格数对计算时长及结果影响较大,因此首先开展了基于物理模型试验数据的网格无关性验证。
试验平台示意如图3所示,整体可分为3部分:定常风洞、透平、数据采集及控制系统。定常风洞实物如图4(a)所示,可造出试验所需的稳定入射气流。装置及后端数据采集系统如图4(b)所示。透平结构尺寸如1.2节所述,其中转子叶片稠度为1.70;数据采集系统主要包括压差变送器、电磁离合器、扭矩传感器、伺服电机、数据采集箱等,其主要作用为实时采集试验过程中气压、透平输出扭矩、透平转速等关键物理量,控制透平启停及转速。试验时,定常风洞给定稳定的5 m/s定常入射流速,通过电磁离合器及伺服电机控制透平的启停并将透平转动后的转速稳定在不同转速,根据式(2)获得不同的流量系数,利用压差变送器、扭矩传感器采集到的实时物理量根据式(3)~(5)计算出透平输出效率,为透平数值模型验证提供数据支持。

图3 试验平台示意Fig. 3 Schematic diagram of test platform

图4 试验平台实物Fig. 4 Physical map of test platform
相同结构尺寸下,选取转子叶片稠度同样为1.70的数值模型,采用realizable k-ε湍流模型,在与模型试验相同工况下进行数值计算,将3.0×106、3.9×106以及5.3×106三种网格数量下的数值计算结果与该装置试验结果进行对比,结果如图5所示。其中,横坐标为流量系数φ,纵坐标为透平定常输出效率η。综合考虑计算时耗及精度,数值模拟研究确定网格数约为3.9×106。
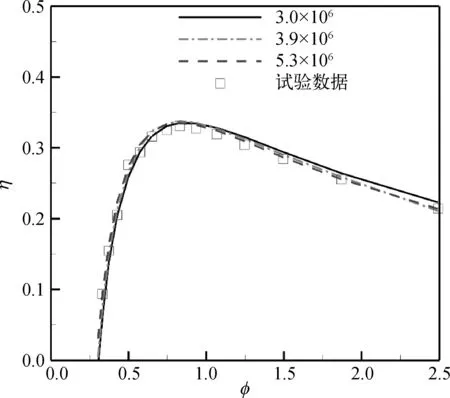
图5 网格数对透平效率的影响Fig. 5 The effect of grid number on turbine efficiency
2.2 数值计算结果分析
计算中所有工况的入射流速大小均为5 m/s,通过给定不同转速以获得不同流量系数下透平运行特性。在实际海况下,流经透平的气流为双向往复气流,因此,在数值计算时给定入口流速为5 m/s(正向气流)和-5 m/s(反向气流)两种流速,以探索不同气流流向下转子叶片稠度对透平定常工作性能的影响。在保证透平其他尺寸、参数不变的情况下,通过对比转子叶片附近的速度分布及透平定常性能评价参数随流量系数的变化规律来考察转子叶片稠度对透平工作性能的影响。
理论上,对于透平机械的叶片,存在一个可使总损失达到最小的最佳叶片数目(或叶片稠度)。在一定轮轴半径下,若转子叶片稠度过大,透平内的气流流道则会被压缩,转子叶片对流体的导向作用增大,但同时摩擦损失也会变大;反之,透平内气流流道较宽,转子叶片对流体的导向作用较差,由流动分离造成的损失会较高。
图6给出了4种典型工况下转子附近速度云图,4种工况为两种入口流速(5 m/s和-5 m/s)及两种转子叶片稠度(1.70和2.34)两两组合形成,4种工况对应的流量系数均为0.83,即正向气流下转子稠度为1.70的透平输出峰值效率对应的流量系数。图6中箭头表示气流方向。如图6(a)所示,气流从下至上流动,在叶片吸力面迎流端发生流动分离,一部分气流沿着吸力面加速流动,并在转子叶片中部形成高流速区,另一部分气流则越过迎流端在压力面发生明显的流动分离现象,并且气流经过叶片中部后与叶片尾部贴合情况并不理想;同时,动叶片吸力面尾端也出现了较大程度的流动分离现象。如图6(c)所示,当叶片稠度增加到2.34时,转子叶片附近流域的宽度减小,转子叶片对流体的导向作用增强,具体表现为:吸力面中部高流速区的峰值及覆盖面积增大;压力面流速分离受到明显抑制;气流流经转子叶片中部后更加贴合叶片尾端流动。当气流为反向流动时,即如图6(b)所示,气流从上至下流动,在转子迎流侧并未发生明显的流动分离,一部分气流沿着吸力面加速流动,并在转子叶片中部形成高流速区,但气流在叶片后半段出现了明显的流动分离,使得透平损失增加。如图6(d)所示,当稠度增加到2.34时,气流在吸力面形成的高流速区扩大,且气流流经转子叶片中部后更加贴合叶片尾端流动。对比图6(a)、(b)及图6(c)、(d)发现,虽然径流式透平可在双向气流下实现单向旋转,但是透平在不同流向气流下所表现出的特性存在较为明显的差异,这与传统的轴流式透平有很大不同,因此在分析透平定常性能时,需同时研究径流式透平在不同流向气流下的工作性能。

图6 转子叶片稠度对叶片附近速度云图的影响(φ=0.83)Fig. 6 The influence of the consistency of the rotor blade on the speed cloud near the blade (φ=0.83)
图7给出了不同转子稠度下透平各定常评价参数随流量系数φ的变化规律,图中横坐标为流量系数φ,φ>0表示透平在正向气流下工作,即入口流速为5 m/s,φ<0表示透平在反向气流下工作,即入口流速为-5 m/s。如图7(a)所示,当气流流向为正向时,在低叶片稠度下叶片稠度对输入系数的影响并不明显,图中σ=1.38与σ=1.70对应下的输入系数变化曲线几乎重合;但是当σ>1.70后稠度对输入系数的影响较为明显,随着转子叶片的稠度增加,在整个流量系数范围内输入系数越大,并且输入系数增大幅度随着流量系数的增大展现的更为明显。当输入气流为反向气流时,σ=1.38、σ=1.70及σ=2.02对应下的输入系数变化曲线几乎重合;当σ>2.02后稠度对输入系数的影响规律与正向气流下相同。
图7(b)为不同转子稠度下透平扭矩系数随流量系数φ的变化规律,整体上,在整个流量系数范围内,扭矩系数随转子稠度的增大而增大。当气流方向为正向时,σ>1.70时扭矩系数的增大幅度明显大于σ<1.70,但当气流方向为反向时,扭矩系数随稠度增加的幅度几乎相同。
图7(c)为不同转子稠度下透平输出效率随流量系数φ的变化规律。稠度对透平效率的影响在整个流量系数范围内均较为明显。当气流方向为正向时,透平峰值效率随着流量系数的增加呈现出先升后降的趋势,其拐点出现在σ=2.34处,此时透平峰值效率最大。然而,稠度对整个流量系数范围内透平效率的影响规律并不同于对峰值效率的影响。在大流量系数下,尤其是在φ>2.0时,虽然透平输出效率随着稠度的增加同样呈现出先增后降的趋势,但其拐点则出现在σ=2.02处。当σ=2.65时,大流量系数下的透平效率随稠度的增加下降极为明显;当φ<0.5时,透平效率始终随着稠度的增加同样呈现出先增后降的趋势,尚未出现拐点。当气流方向为反向时,透平峰值效率随转子叶片稠度的变化规律与正向气流相似,其峰值效率的拐点同样出现在σ=2.34处。
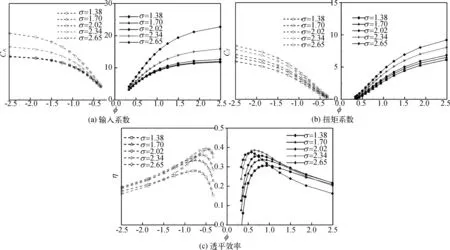
图7 转子叶片稠度对透平性能的影响Fig. 7 The influence of the consistency of the rotor blade on turbine performance
表4为不同转子叶片稠度对透平输出峰值效率的影响,从图7中还可看出:1)峰值效率随着转子叶片稠度的增加有明显的先升后降的趋势,不同流向下透平输出峰值效率拐点均出现在σ=2.34处。当入射气流为正向时,最大峰值效率为38.6%,当入射气流为反向时,最大峰值效率为39.7%;2)随着转子稠度的增加,透平峰值效率所对应的流量系数逐渐减小。以正向气流为例,当σ=1.38时透平峰值效率出现在φ=0.83处,但当σ=2.65时,透平峰值效率则出现在φ=0.57处;3)当入射气流方向发生变化时,即使流速大小相同,峰值效率对应的流量系数也存在偏差。以σ=2.34为例,正向气流下峰值效率出现在φ=0.65,而反向气流下峰值效率出现在φ=0.50。

表4 不同转子叶片稠度对峰值效率的影响Tab. 4 The influence of different rotor blade consistencies on peak efficiency
综上所述,在轮轴半径相同条件下,综合考虑正向、反向气流下透平在整个流量系数范围内输出效率,透平在σ=2.34时的工作性能最优。
3 结 语
通过定常数值计算,在不同气流流向下探索了不同转子叶片稠度对径流式空气透平工作特性的影响规律。研究结果表明:1)虽然径流式透平可在双向气流下实现单向旋转,但当气流方向不同时,透平展现出的定常工作性能存在明显差异,其差异主要包括转子叶片周围的流场,输入系数、扭矩系数随转子叶片稠度的变化趋势,输出效率的峰值及对应的流量系数;2)稠度对透平效率的影响在不同流量系数范围内也同样存在差异,在大流量系数下透平输出效率随稠度的增加先升后降,而在小流量系数下,尤其是在φ<0.5时,透平输出效率随着稠度的增加而增加,尚未出现拐点。因此,综合考虑气流流向、透平整个工作范围内输出效率,在轮轴半径相同条件下,当转子叶片稠度为2.34时透平定常工作性能最优。

