深水极端波浪非线性几何特征试验分析
赫岩莉,毛鸿飞,吴光林,潘新祥
(1. 广东海洋大学 海洋工程学院,广东 湛江 524088; 2. 广东海洋大学 海运学院,广东 湛江 524088)
在真实海洋中,波浪常以波群形式传播,在传播过程中,波浪非线性作用会使得波高增加[1],形成极大波,这些极大波浪及其破碎正是引起海上事故的主要原因之一。目前,针对野外实测,由于测量难度大、工作人员安全不能得到很好保障、经济成本较大等原因,难以很好地捕捉波浪的多种形态,从而使得波浪演化过程中几何特征和变化规律的深入研究受阻。采用具有可重复性的物理试验对波浪进行多次采集,分析其演化变形及非线性现象产生机理是目前常用的有效研究方法。
在波浪演化过程中,随着非线性增加,波浪开始变形,波前前倾,波面幅值增加,波面不再对称。针对波浪演化的复杂变化及破碎波几何特征,学者们已经进行了相关研究。早在1891年,Stokes[2]建议当波顶角大于等于120°时,波浪发生破碎。Myrhaug和Kjeldsen[3]通过分析极端波浪的峰前陡、竖直和水平不对称因子,对极端波浪的不对称性进行分析。Bonmarin[4]针对深水陡波演化至波浪发生破碎阶段进行了试验观察研究,尤其针对波浪接近破碎区域的波形不对称情况进行了分析,指出不对称增长率与破碎类型紧密相关,卷破波不对称性要比崩破波更明显。Wu和Yao[5]对试验结果分析指出谱斜率和频带宽对极端波浪的变形和几何特征起到关键作用。陈洪洲等[6]采用物理试验对浅水极端波浪几何特征进行研究,指出坡度对极限波陡和偏度影响较小,但对不对称度具有明显影响,随着坡度增加,不对称程度更明显。高志一[7]指出,波群包络线不对称性可导致最大波高提前一个波长出现。随后,高志一和文凡[8]通过分析波群结构及波浪破碎特征得到,在波群前端波动振幅较大,波面不对称性导致前端单个波的波陡较大,从而易发生破碎。梁书秀等[9]的深水试验分析结果给出,波浪发生破碎后,由于能量减小导致特征频率减小、特征周期增加。在波浪演化过程中,非线性使得波面发生严重变形,研究其产生机制是了解波浪变化的关键。Diorio等[10]采用不同方法产生破碎波浪,通过测量接近破碎处波峰波面指出,在缩放适当条件下,当破碎开始时,崩破波峰前端的凸起和毛细波是自相似的,不依赖于破碎波产生机制。Benjamin和Feir[11]最初从理论上给出调制不稳定是引起深水极端波浪的机制之一。在此之后,Bonmarin和Ramamonjiarisoa[12]通过对深水破碎波变形分析指出,破碎主要是由调制不稳定和快速增长的不稳定引起,前者使得局部波陡趋近于一个最大值,后者直接导致破碎发生。Tian等[13]通过分析色散聚焦和调制不稳定机制引起的波浪破碎波长下降情况得到,无论是崩破还是卷破,在破碎开始前两个周期内,波长下降率均约为30%;同时,在破碎开始前一个周期内,崩破波峰增长约20%,而卷破约增长40%。
综上,多年来,极端波浪几何非线性特征一直是水波动力学研究中难点与热点之一,目前尚未有统一的结论。采用试验方法对极端波浪进行深入分析是了解其物理特征的重要途径之一。海洋中大多破碎类型为崩破,为更接近海浪真实情况,采用调制不稳定为主要机制生成极端波浪进行其动力学特征分析。
1 试验布置及参数介绍
1.1 试验布置
试验在大波流水槽中进行,水槽尺寸为48.6 m×2 m×1.8 m(长×宽×高),试验水深1 m,俯视图见图1。水槽一端为液压驱动式活塞型造波板,另一端采用消浪网作为吸波装置。在以往试验中,频率为1 Hz的波反射系数约为5%,则可认为反射对试验影响较小,故在此试验中忽略不计。该试验中,将造波板平均位置定义为零点x=0 m,波浪传播方向C如图1所示。

图1 试验水槽俯视图Fig. 1 Top view of experimental tank
为保障波浪二维传播,将一个光滑水泥墙安装在水槽中间,使得水槽分为0.8 m和1.2 m两部分,选择0.8 m 宽度部分作为有效试验区域。在试验中,沿水槽长度方向共布置34个测点采集数据,在x=12.9 m以前部分,测点间距为2 m;在x=12.9 m以后部分,测点间距为1 m。浪高仪绝对精度为±1 mm,在进行试验之前,对所有浪高仪进行了稳固性检查和校准。为减小造波机产生的非传播波影响,首测点位置布置在x=4.9 m 处,并以此处测量结果校准波群初始参数。
1.2 参数介绍
采用高斯波群为研究目标,对其演化过程中产生的极端波浪非线性动力学特征进行分析。在试验中,采样频率fs=50 Hz,采样时间间隔为Δt=0.02 s,采样点数为8 192,载波波数k0=4.03>1,满足深水条件。试验中造波函数与Shemer等[14]研究相同:
ζ=Apexp[-(tf0/N)2]cos(2πf0t)
(1)
其中,Ap是造波机运动冲程幅值;N是波群包络宽度,也称为波群宽度,N与频带宽Δf关系为:
(2)
其中,载波频率f0=1 Hz,Δf为频带宽,根据谱峰值一半所截幅值谱的宽度确定。在试验中,造波机为推板式,其水力传递函数为:
(3)
通过式(3)可得到初始位置处最大波面升高A0=ApTrsfun,波陡为ε0=k0A0,具体试验波况见表1。

表1 高斯波群初始波况Tab. 1 Initial wave condition for Gaussian wave group
2 试验结果几何特征分析
众多研究已表明[3,17],在传统研究中,只采用波高和波长比值定义的波陡对不对称陡波特性进行分析是不够的。继Myrhaug和Kjeldsen[3]后,Babanin等[18]指出偏度Sk和不对称度As是水波的自然特征。偏度是波面关于水平轴的对称参数,其值大于零,说明波峰大于波谷值,即为典型的表面波;不对称度As是波面关于竖直轴的对称参数,As小于零,说明在波浪传播方向,波浪前倾。偏度和不对称度两者结合,共同表现波浪在传播过程中的非线性特征变化。
2.1 偏度Sk特征演化
为更好提取数据有效信息,在分析数据之前,采用5 Hz为截止频率的低通滤波对数据进行去噪处理。波浪在传播过程中,由于非线性作用,使得波面发生明显不对称现象,见图2,示例波况为GP8。图2(a)为x=4.9 m处波面,图2(b)为波浪传播至x=13.9 m处波面情况,此时波面升高达到最大值0.1 m。由表1得,对应该波况BFI值为2.151,根据Janssen[15]研究可知,调制不稳定发生。比较两图可知,随着传播距离增加,由于调制不稳定和高低阶谐波非线性作用,波形由对称逐渐变化为不对称状态,几何形态发生明显变化。
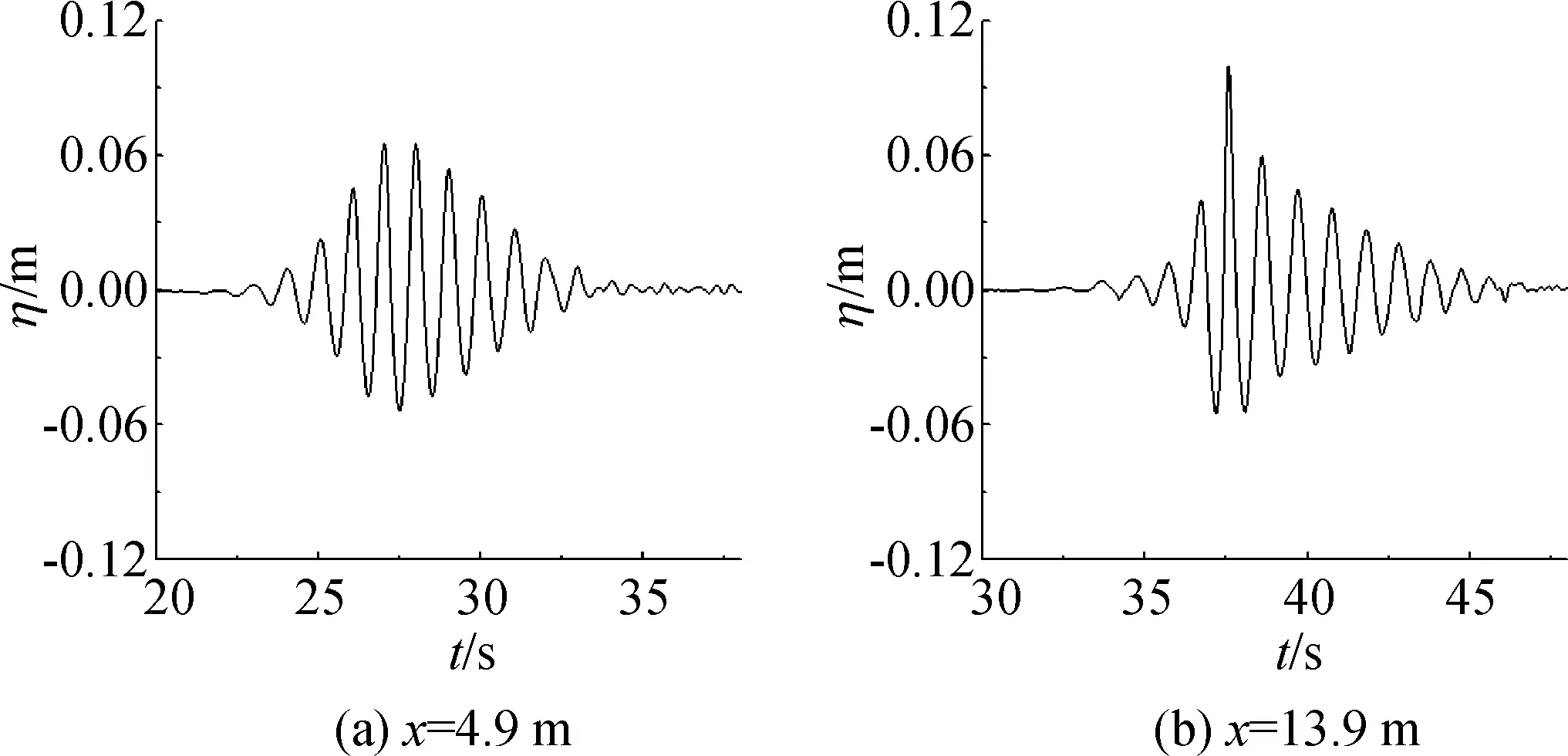
图2 GP8波面变化Fig. 2 Variation of wave surface elevation for GP8
为深入研究极端波浪在传播过程中几何特征变化情况,采用与Ma等[19]研究中相同定义的波面偏度Sk和不对称度As对试验数据进行分析。在此之前,首先给出波群各参数定义,如图3所示,ηm、ηf和ηr为波峰值以及与其相邻的前后两个波谷值,其中ηf和ηr为负值;th和tr分别对应两个波谷最大幅值发生时刻,tm为最大波面升高发生时刻;t1、t2、t3和t4为与波峰和两个相邻波谷相关的过零点发生时刻。文中偏度Sk定义为:

图3 波群几何参数示意Fig. 3 Sketch of geometric parameters for wave group
(4)
令tf=tm-t2,tr=t3-tm,thf=th-t1,thr=t2-th,trf=tr-t3,trr=t4-tr,采用Ma等[19]研究对不对称度As定义为:
(5)
同样地,可分别给出对应两个波谷的不对称度Als和Ars定义为:
(6)
(7)
针对未发生破碎波群,其偏度Sk演化情况如图4所示,图中竖直划线表示最大波面升高发生处。由图4(a)可见,在首测点位置处,由于波前作用使得波面偏度大于0,由于初始波陡较小,波面呈现微小不对称。随着传播距离增加,Sk从正值逐渐过渡到负值后趋近0,整体Sk变化幅度较小。保持其他条件不变,当增加波陡后,Sk呈现大幅度变化,见图4(b)。根据Sk均为正值且偏离零值较大可知,随着波浪演化波峰逐渐增大。根据表1可知,该波况对应BFI值为1.383,即调制不稳定发生。随着波浪传播,由于三阶共振作用,产生新的自由波,使得非线性增强,从而在x=10.9 m处产生大波,因此使波面偏度发生明显变化。图4(c)为增加群宽度后Sk演化情况,结果显示,当保持较小波陡、增加群宽度后,Sk逐渐增加至0.3左右然后开始减小,直至最后接近于0。说明增加群宽度使得偏度增加,波面不对称性增加,但因波陡较小,非线性较弱,最终波面在演化一段距离后接近于对称形状。
当增加波陡后,波浪非线性增强,破碎发生,Sk演化情况如图5所示,阴影区域代表破碎发生区域。由图5所示,与图4比较,破碎波群偏度呈现明显不同的变化。从波浪开始传播,Sk持续上涨,其最大值(甚至超过1)发生在破碎区域内。由此说明,波峰逐渐变尖,尤其在破碎区域,波面发生严重变形。需要注意的是,在破碎区域内,Sk呈现出几次超过开始破碎时其值的情况,对应试验中间歇性发生的多次破碎。当Sk达到极大值时,波峰异常尖锐,波谷平缓,波面严重不对称,同时破碎发生,这也说明Sk可能作为判断破碎发生的一个标志。随着传播距离增加,经历破碎之后,由于破碎和黏性等因素,波浪损失大量能量,Sk逐渐趋向于恢复至初始状态。
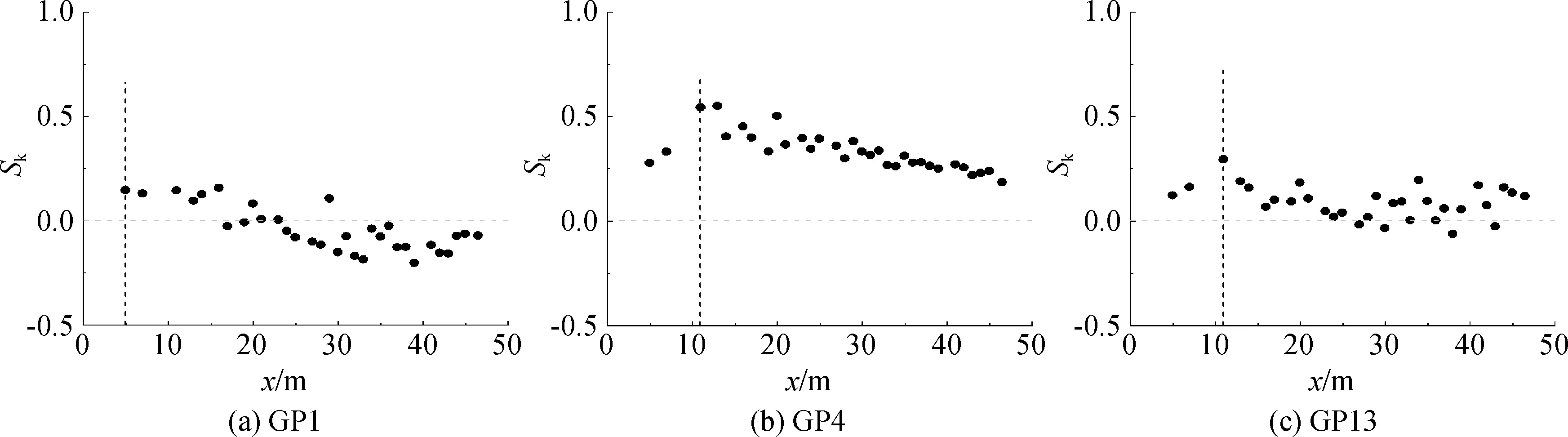
图4未破碎波群偏度Sk演化Fig. 4 Evolution of skewness Sk for non-breaking wave groups

图5 破碎波群偏度Sk演化Fig. 5 Evolution of skewness Sk for breaking wave groups
2.2 不对称度As特征演化
由以上分析可知,根据初始条件不同,随着波群演化,波面会产生不同程度不对称变形。针对其不对称性,这里从最大波峰及其相邻两个波谷情况分别进行分析。图6为波陡依次增加后波群波峰不对称参数As演化情况,由图可见,随着波陡增加,非线性增加,As变化幅度明显增加。尤其当接近破碎(图6(c))或发生破碎(图6(d))时,As值大于0.5,甚至接近于1,说明波峰前后两端发生强烈不对称变形。
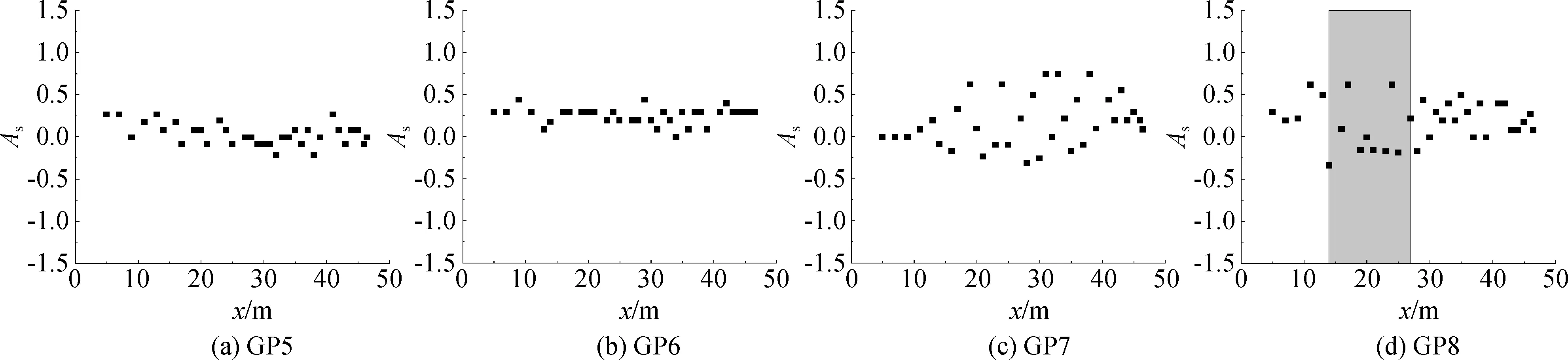
图6 不同初始波陡波群的波峰不对称度As演化Fig. 6 Evolution of asymmetry As of crest for wave groups with different initial wave steepness
当保持波陡不变,增加波群宽度以后,波峰不对称度As演化情况如图7所示,阴影部分为破碎区域。由图7可见,在破碎区域内,由于强烈非线性使得不对称度发生大幅度变化,As最大值可超过1,此时波峰变形严重;同时针对破碎波群,As最大值也发生在破碎域内,即波峰严重变形情况发生在破碎区域。

图7 不同群宽度波群的波峰不对称度As演化Fig. 7 Evolution of asymmetry As of crest for wave groups with different wave group widths
以上针对不同初始条件下波群的波峰不对称性进行了分析,下面对与其相邻两个波谷的不对称性进行分析。图8为不同波陡情况下,波峰前端波谷不对称度Als演化情况。由图8可见,随着波陡增加,非线性增加,Als出现增长,尤其当波浪发生破碎时,在破碎区域,Als较大;与波峰情况类似,此处峰前波谷也出现明显变形。

图8 不同初始波陡波群的波峰前端波谷不对称度Als演化Fig. 8 Evolution of asymmetry Als of trough in front of crest for wave groups with different initial wave steepness
保持波陡不变,增加波群宽度,Als演化如图9所示,阴影部分为破碎区域。当波陡较大、波群宽度较小时,如图9(a)所示,波群峰前波谷不对称性较稳定,变化幅度较小。这说明在未发生破碎情况下,峰前波谷变形相对稳定,峰前波谷相对对称。当继续增加波群宽度之后,谱宽减小,在相同波陡情况下,波浪发生破碎,如图9(b)~(d)所示。图9(b)~(d)中显示,在破碎带内,Als变化范围突然变大,随着波群宽度增加,其变化范围从-0.1 ~ 0.7发展到-0.3~1.1之间。尤其当Als超过1时,在波峰前端、与波峰相邻的半个波谷变的非常窄,而另一半波谷宽度是其二倍以上,说明峰前波谷变形非常严重。
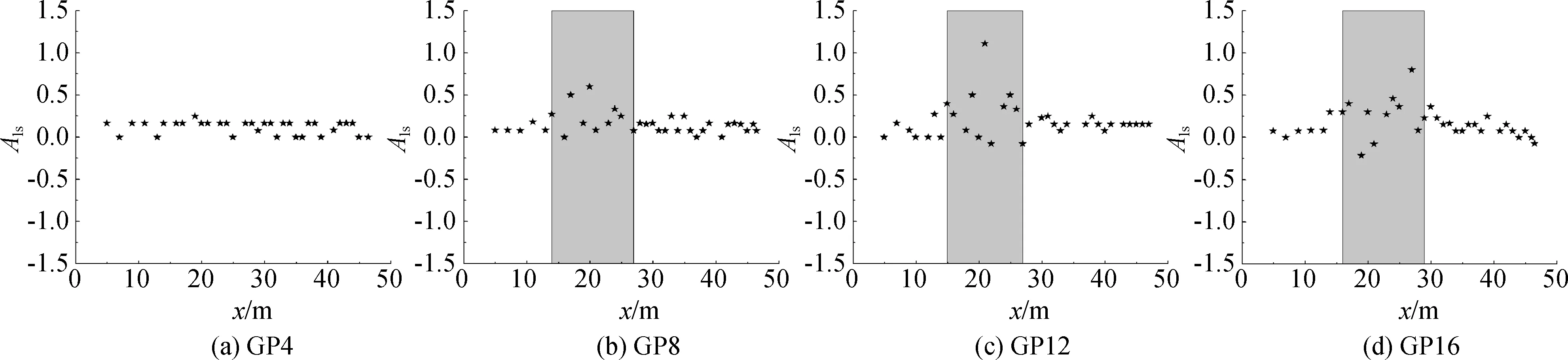
图9 不同群宽度波群的波峰前端波谷不对称度Als演化Fig. 9 Evolution of asymmetry Als of trough in front of crest for wave groups with different wave group widths
由以上分析可见,波浪在演化过程中,波峰以及峰前波谷在波陡和谱宽影响下,都会呈现不同程度变化。同样地,针对峰后波谷不对称性Ars,目前研究也很少,因此对其也进行了分析。当波群宽度相同时,随着波陡增加,Ars演化情况如图10所示,阴影部分为破碎区域。由图10可见,随着波陡增加,峰后波谷不对称性有所增加,但增加幅度小于峰前波谷。

图10 不同初始波陡波群的波峰后端波谷不对称度Ars演化Fig. 10 Evolution of asymmetry Ars of trough behind crest for wave groups with different initial wave steepness
维持波陡不变,增加波群宽度,谱宽减小,Ars变化情况如图11所示,阴影部分为破碎区域。由图11可见,随着波群宽度增加,峰后波谷不对称度也有明显增加;同样地,与Als相比,Ars增加幅度相对小。

图11 不同群宽度波群波峰后端波谷不对称度Ars演化Fig. 11 Evolution of asymmetry Ars of trough behind crest for wave groups with different wave group widths
综上所述,通过对波峰以及与其相邻两个波谷不对称度分析可知,增加波陡或波群宽度,均使得波浪非线性增加,从而波峰和两侧波谷均发生不同程度不对称,使得波群携带主要能量部分的波面发生明显变形。当改变波陡或波群宽度后,波峰不对称度As发生强烈变化;波峰前端波谷不对称度Als也有明显变化,但变化程度小于波峰;变化最小的是波峰后端波谷不对称度Ars。
3 幅值谱特征
当初始条件不同时,波面变化呈现差异很大,随着波浪传播,由于波波相互作用和三阶共振作用可分别产生高低阶谐波和新自由波,使得幅值谱发生很大变化。图12给出以破碎波群GP16为示例对应的对数坐标下幅值谱演化情况,虚线表示首测点处幅值谱,标记ηmax处表示最大波面升高发生处(破碎发生)。由图12可见,随着波浪趋近于破碎点处,谱峰能量开始向低频转移,当达到最大波面升高发生处,破碎发生,出现明显频带下移现象,经过破碎区域后,主频能量没有向初始主频恢复,并呈现出永久频带下移现象。峰频变化对后续波浪演化及相关特性等会产生很大影响,如Gao等[20]数值研究指出,当谱峰频率等于或者接近港湾共振频率之一时,聚焦波群可直接引起港湾共振现象。

图12 波况GP16幅值谱演化Fig. 12 Evolution of amplitude spectrum for Case GP16
针对文中试验数据,对其频带下移量Δfd进行了研究分析。其中,对于未破碎波群,频带下移量采用首尾测点处无量纲化主频差来确定;对于破碎波群,频带下移量采用频带下移开始发生处X与最后测点处的无量纲化相对主频差来确定,无量纲化参数均为首测点处主频,结果见表2。

表2 频带下移量Tab. 2 Frequency downshift
根据表2中结果所示,随着波陡增加,Δfd整体上呈现增加趋势且频带下移倾向于更早发生;同时,宽波群整体频带下移量较大。当波陡较小时,非线性较小,增加波群宽度,在波浪演化过程中未出现频带下移现象。当波陡增大后,针对未发生破碎波群,频带下移量随着波群宽度增加而增加,如表2中GP2、GP6、GP10和GP14所示。继续增大波陡,针对未发生破碎波群,频带下移量较小;然而针对发生破碎波群,频带下移量有明显增加,如表2中GP3、GP7、GP11和GP15。如继续增大波陡,未破碎波群依然具有较小的频带下移量,但随着波群宽度增加,破碎波群具有更大且一致的频带下移量。这说明,在波浪演化过程中,频带下移量与波陡、波群宽度和波群是否发生破碎密切相关。
调制不稳定是频带下移产生机制之一,赫岩莉等[21]的试验研究指出,较大频带下移量对应的BFI一般也较高。结合文中试验波浪在演化过程中出现不同程度频带下移现象,对频带下移量与BFI是否相关,进行了分析。如图13所示,当BFI>1时,几乎所有波群均发生了不同程度的频带下移情况,随着BFI增加,频带下移量整体呈现明显的上升趋势。

图13频带下移量Δfd与BFI的关系Fig. 13 Relation between frequency band downshift Δfd and BFI
4 结 语
通过物理试验,对多种初始条件下的高斯波群几何特征以及幅值谱特征进行了分析,得到以下主要结论:
1) 随着波陡或波群宽度增加,非线性增强,波峰逐渐变尖,波面发生明显变形,偏度Sk呈现大幅度变化。尤其在破碎区域,Sk的多次极大值对应着间歇性发生的破碎,也说明Sk可能作为判断破碎的一个指标。
2) 通过对波峰以及与其相邻两个波谷的不对称度分析得出,增加波陡或波群宽度,均使得波浪非线性增加,从而波峰和两侧波谷均发生不同程度不对称。其中,波峰不对称度As所受影响较大。其次是波峰前端波谷不对称度Als,同时Als变化程度与破碎情况紧密相关,当波陡较大时,波群未发生破碎,Als变化较小;反之,当波群发生破碎后,Als会呈现剧烈变化。所受影响较小的是波峰后端波谷的不对称度Ars。
3) 随着波陡增加,频带下移量增加且频带下移倾向于更早发生,同时,宽波群整体频带下移量较大。频带下移量与波陡、波群宽度以及破碎情况相关:保持较小波陡不变,针对均未发生破碎的多个波群,随着波群宽度增加,频带下移量快速增加;将波陡增加后,对应该波陡,波群发生未破碎和破碎两种情况,随着波群宽度增加,破碎波群的频带下移量要大于未破碎波群,且对应该波陡下破碎与未破碎波群,两者频带下移量分别保持不变。当BFI>1时,随着BFI增加,频带下移量呈现快速增长趋势。

