非淹没刚性植物对海啸作用下海堤水动力特性影响数值模拟研究

蒋昌波，熊玉章，屈 科，邓 斌，陈 杰

(1. 长沙理工大学 水利工程学院，湖南 长沙 410114； 2. 水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114； 3. 洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙 410114)

海堤作为沿海地区抗御台风及风暴潮灾害的重要海岸保护设施，其在保障沿海经济社会发展和人民群众生命财产安全方面发挥了重要作用[1]。近年来,随着全球气候变化，极端灾害事件日益频发，海堤的重要作用更加凸显。然而，海堤堤顶高程由于经济条件和地基承载力的限制不可能无限制增加，这就导致海啸发生时，海堤越浪现象无法避免。许多严重的海堤破坏事件都是由堤顶越浪造成。例如：极端波况作用下，荷兰、德国和丹麦均发生过海堤堤顶越浪失稳现象[2]。国内外学者通常把越浪量[3-5]作为衡量海堤自身及堤后安全性和防浪有效性的重要指标，实际上，海堤稳定性主要取决于波浪越浪过程引起的瞬时荷载[6]，因此，仅以平均越浪量作为安全评价标准是不全面的。波浪越浪过程引起的瞬时荷载通常可以用越浪流厚度及流速来评估。Möller等[7]认为破波越过堤顶，越浪水流与海堤土体之间相互作用将导致堤顶表面产生侵蚀破坏。Schüttrumpf等[8]分析了以往海堤破坏事件，认为海堤的破坏主要是由于个别极端波况引起的，特别是与之相关的越浪流厚度和流速可以用来预测海堤是否会发生侵蚀、渗透和滑移破坏，并由此对海堤前坡、堤顶、后坡水流厚度和流速空间分布规律展开讨论，Van Bergeijk等[9]基于大量的实测数据提出两个公式来预测海堤堤顶和后坡最大流速，这一最大流速对评估波浪侵蚀作用和海堤稳定性具有重要意义。近些年来，越来越多的学者开始广泛关注越浪流的流场特征[10-12]。

海堤虽然是一种较好的海岸硬防护措施，但是也存在一定的弊端。例如：海堤形成的反射波常常会加重堤前岸滩的侵蚀，造成严重的冲刷。实际工程中，通常采用软防护与硬防护结合的方式以达到海岸防护的最佳效果。其中，海岸植被是一种有效的海岸软防护措施。对2004年印度洋大海啸的灾后调查发现，沿岸生长的红树林类刚性植物能对海啸波起到显著的削弱作用[13]。因此，种植海岸植被是一种绿色环保的海啸防御措施。国内外学者针对海岸植被消波特性从现场观测[13-15]、物理试验[16-18]、数值模拟[19-21]等方面开展了大量的研究工作。海岸植被消波主要受水动力因素和植物因素的影响，其中水动力因素主要有波高、周期、水深和来流条件等，如Yin等[22]通过改变入射波要素和来流条件分析了波流共同作用对非淹没刚性植物消波的影响；而植物因素主要包括植物种类、分布特征、组成部分等，如Wu等[23]通过数值试验对比了刚性、柔性植物影响下的沿程波高变化，Iimura等[24]通过物理与数值试验相结合的方法研究了不同植物分布特征(“前疏后密”、“前密后疏”、“均匀分布”)对海啸波衰减及爬高的影响，He等[25]考虑了植物根、茎、叶等因素，对波浪沿程波高、透射系数以及植物拖曳力系数变化规律进行了物理试验研究。上述研究主要是考虑“植物”单一系统对波浪水动力特性的影响，与此同时，海堤的研究也只考虑单一的海堤或关注于海堤—浅堤组合情形下的水动力特性[26-28]。随着生态护岸理念的推广，海岸植被与海堤相组合日益成为新的海岸防护措施。比如：越南湄公河三角洲采用“植物—海堤”组合方式来降低海啸带来的危害[29]。海啸波在经过植物区后与海堤相互作用水动力特性较无植物情况有所不同，需要考虑波浪经过植物覆盖区域后的变化情况[30]。因此，有必要开展“植物—海堤”组合系统下的极端波浪水动力特性研究。

虽然近年来有部分学者认为孤立波不能准确地模拟海啸波，但是其在传播过程中能够维持稳定的波形以及与长时间传播的海啸具有相似的形态[31]，因此，孤立波目前仍然作为一种有效的类海啸波型。基于非静压单相流模型NHWAVE，通过合理设置计算工况，采用孤立波近似海啸波的首波，研究了不同入射波高，植物分布密度、分布宽度影响下，沿程波形、波高变化，以及海堤堤顶流厚度、流速空间分布规律，并与无植物情况进行对比，研究结果可为相应的海岸工程建设提供参考依据。

1 理论模型

1.1 控制方程

NHWAVE的控制方程为σ坐标系下的连续性方程和动量方程，如式 (1)和(2) 所示：

(1)

(2)

采用k-ε湍流模型，其控制方程为：

(3)

(4)

式中：(i,j)=1,2,3;x1=x,x2=y,x3=z代表笛卡尔坐标系中三个方向的坐标；湍流黏性系数υt=CDk2/ε；其它的参数为常系数。

NHWAVE模型[32]采用有限体积与有限差分相混合的方法并结合Godunov型格式[33]对控制方程进行空间离散，其中速度项定义在网格单元的中心位置，压力项定义在网格单元的竖直方向界面位置；采用二阶非线性龙格—库塔方案(SSP Runge-Kutta)进行时间步迭代。计算域左侧为波浪入口边界，右侧为消波边界；底部边界法向速度满足运动学边界条件，水平速度满足滑移边界条件；侧向边界满足滑移边界条件。NHWAVE模型具体数值方法可参考文献[32]。

1.2 拖曳力系数

(5)

其中，α0、α1是仅与植物分布密度有关的经验系数，Rep为基于植被区内孔隙流速的雷诺数。

Huang等[34]指出在特定情况下如孤立波与植物相互作用时，植物雷诺数Rep处于103数量级，远大于α0。故上述公式可以简化为CD=2α1，即CD值与植物的布置和植物区的分布长度无关，只与植物的分布密度有关，并依据试验数据进一步推导出孤立波与非淹没刚性植物相互作用的拖曳力系数经验公式，具体表达式为：

CD=1.245+4.587φ/(1-φ)

(6)

2 模型验证

2.1 孤立波与植物相互作用模型验证

采用Huang等[34]的试验数据来验证NHWAVE模型计算植物消波的准确性。试验在长32 m，宽0.55 m的玻璃水槽中进行，植物模型由有机玻璃管制作而成，单株植物模型直径为0.01 m，放置于水平槽底中央。植物3种不同的排列方式如图1(a)所示，排列A、B、C对应的植物分布密度φ分别为0.175、0.087、0.044。试验设置了三种不同植物宽度W分别为0.545、1.090和1.635 m，对于不同植物带宽度下浪高仪安放位置如图1(b)所示。

图1 植物排列方式及浪高仪安放位置Fig. 1 Arrangement of vegetation and layout of gauges

文中共验证5组不同的算例，水深均为0.15 m，验证工况如表1所示。数值水槽长度为20 m，水平网格尺寸为0.01 m，时间步长为0.01 s，模拟时长30 s，不同密度分布的植物按照式(6)求得相应的拖曳力系数。为了确定竖直网格的层数，对竖直网格的收敛性进行验证。以工况A1条件下测点G1处自由液面为例，垂向分别设置5层、10层、20层网格，自由面η随时间变化的模拟结果如图2所示，其中垂向设置5层、10层与20层网格的计算结果基本完全重合，说明加密网格后模拟结果无明显改进。因此，垂向设置10层网格，其网格尺寸符合计算精度要求。

表1 验证工况Tab. 1 Parameter setup for validation cases

图2 网格收敛性验证Fig. 2 Simulation results for grid convergence

将数值模拟计算结果与Huang等[34]的试验数据进行对比，图3(a)、(b)为工况A1、B2的自由液面验证结果，实测值与模拟值拟合良好。对于工况A1，浪高仪G1记录自由液面随时间变化序列的两个峰值点，分别对应入射波高和反射波高，浪高仪G5则用来记录透射波高数据列，从中不难看出，经过植物区后，透射波仍以孤立波形式继续向前传播，波形由尖陡变得平缓。对于工况B2，由于植物分布密度较小，反射波浪不太明显，隐藏在一连串起伏不定的尾波中。图3(c)为工况C1、C2、C3下，沿程相对波高变化验证结果，随着植物分布宽度的增大，沿程波高衰减程度增大。从图3验证结果不难看出，NHWAVE模型可以有效模拟孤立波与植物相互作用过程中波浪的传播变形及波高沿程变化，使用经验公式计算出的拖曳力系数可以准确地模拟植物对孤立波的衰减作用。

图3 工况A1、B2自由液面验证及C1、C2、C3沿程相对波高验证 Fig. 3 Verification of surface elevation for A1 and B2 and verification of relative wave height for C1,C2 and C3

2.2 孤立波越浪模型验证

采用Hunt[36]的试验数据来验证NHWAVE模型计算孤立波爬坡与越浪过程的可靠性。验证工况为孤立波波高0.1 m，静水深0.5 m，波浪经过1∶20的斜坡，再与斜坡上的海堤相互作用，发生爬高和越浪现象。海堤顶部水平，两侧斜坡坡度约为1∶2，海堤具体形状尺寸可参考文献[36]，数值试验布置如图4所示。斜坡坡脚距离造波机8.33 m，海堤堤脚距离斜坡坡脚8.13 m，30个浪高仪记录沿程波高变化。

图4 斜坡海墙上孤立波越浪计算区域布置Fig. 4 Computational layout solitary waves overtopping on a sloping seawall

二维数值水槽长度为22 m，水平网格尺寸为0.01 m，时间步长为0.01 s，模拟时长20 s，数值试验的地形及浪高仪布置与物理试验相同。为了确定竖直网格的层数，对竖直网格的收敛性进行验证。以t=10 s时自由液面空间变化为例，垂向分别设置5层、10层、20层网格，模拟结果如图5所示，其中垂向设置5层、10层网格与20层网格的计算结果基本完全重合，说明加密网格后模拟结果无明显改进。因此，垂向设置10层，其网格尺寸符合计算精度要求。

图5 网格收敛性验证Fig. 5 Simulation results for grid convergence

图6显示的是孤立波在传播过程中t=10 s、11 s、12 s、13 s时自由液面的空间变化过程。

图6 不同时刻自由液面的空间变化Fig. 6 Spatial variation of free surface elevation at different time instances

其中横坐标x表示沿正方向与数值水槽左边界距离，纵坐标η表示自由液面空间变化，图6中右侧几何图形代表斜坡上的海堤。孤立波与海堤相互作用大致可分为4个过程：1)孤立波在斜坡上传播发生浅水变形，波高逐渐增大，波浪前倾，波形变得不对称；2)孤立波与海堤相互作用，由于阻水效应，波浪不对称性增大；3)孤立波到达海堤，水流越过海堤堤顶，发生越浪现象；4)破碎之后的波浪分为两股，分别为越浪流和回落流。越浪流继续爬坡，而回落流从海堤顶回退至自由液面。从图6不难看出，NHWAVE模型可以较为正确地模拟出孤立波与海堤相互作用过程中波浪的爬高和越浪现象。

3 工况设置

为研究非淹没刚性植物对海堤水动力特性的影响，文中建立了数值波浪水槽，数值水槽布置如图7所示。沿水槽长度方向为x轴，垂直向上为z轴，坐标原点位于左侧造波边界，计算区域为35 m，右侧设置有长度为5 m的消波区域。海堤堤脚位于x=20 m处，前坡坡度为1∶5，后坡坡度为1∶2，堤顶水平段长为0.3 m，堤高为0.17 m。植物区右侧距离海堤堤脚5 m，模型置于x=13.5～15.0 m处，植物高度设置为0.8 m以保证各种工况下均达到非淹没状态。水平网格为0.01 m，垂向设置10层，时间步长为0.01 s，模拟时长30 s，为满足计算稳定性的要求，计算均采用自适应时间步长，最大CFL数设置为0.2。

图7 数值水槽计算区域布置Fig. 7 Computational layout for numerical flume

所有工况水深均为0.15 m，分别考虑了3种波高、植物带分布宽度、分布密度，共设置27种工况，按照式(6)得到相应的拖曳力系数。试验工况详见表2。沿程设置21个浪高仪测量自由液面的时间变化。11个浪高仪沿海堤堤顶均匀布置(G9～G19)，沿植物区均匀布置3个浪高仪(G2～G4)，G1距离植物区左端0.3 m，用来测量入射波浪。G5距离植物区右端0.3 m用来测量透射波浪，G6位于植物区右端与海堤堤脚中间，用来测量海堤对透射波传播的影响，海堤前坡在堤脚和中间位置设置2个浪高仪(G7、G8)用来测量透射波浪在海堤上的浅水变形，后坡同样设置2个浪高仪(G20、G21)。

表2 数值模拟工况设置表Tab. 2 Parameter setup of numerical simulation

(续表)

4 结果分析

4.1 波形沿程变化

图8为波高H=0.05 m的入射波与分布宽度W=1.0 m，分布密度φ=0.087的植物区相互作用时，即工况18条件下，浪高仪G1、G2、G4、G6、G7、G9处自由液面η的历时曲线。

图8 工况18条件下G1、G2、G4、G6、G7、G9位置自由液面历时曲线Fig. 8 Time series of free surface elevation at location G1,G2,G4,G6,G7,G9 in case 18

从图8(a)可以看出G1测量的自由液面存在3个明显的峰值，首先出现的为入射波波峰，随后出现的为因植物区反射造成的反射波波峰，最后为海堤反射造成的波峰；在G2处，孤立波由于植物的阻挡产生壅高，随后孤立波进入植物区(x=14～15 m)，G4处植物对波浪水质点的运动产生干扰，孤立波波高急剧减小，透射波仍以孤立波的形式向前传播，波形由尖陡变得平缓，同时对比图8(b)、(c)可以发现，植物不光能消减入射波能，还能消减海堤反射波能，当植物分布密度越大时，消减效果越明显；G6处由于海堤的壅阻效应，透射波波高有所增加，G7位于海堤堤脚位置，由于浅化作用，透射波波高变陡，与此同时，由于海堤反射造成的反射波开始与透射波分离，反射波后面紧接着出现一个明显的水位降低，这是水流越过堤顶后产生较大的回流，导致靠近海堤前侧附近的水位低于平均水面；G9处透射波浪完全破碎，水体开始在堤顶延展开，发生越浪现象。

4.2 波高沿程变化

图9分别给出了在不同波高、不同植物分布密度和不同植物分布宽度情况下，孤立波沿程波高变化情况。考虑某单一变量时，其它两种变量保持不变，图9(a)对应工况7、16、25，图9(b)对应工况16、17、18，图9(c)对应工况10、13、16。图9中5个测点，分别为浪高仪G2～G6所测得的数据，采用浪高仪G1处波高H1进行无量纲化处理，其中x′/h=0处对应浪高仪G2所在位置，h为水深。H5为x=15.3 m处(距离植物带末端0.3 m)波高，Hi为植物带沿程各浪高仪测点处波高，H5/H1表征了孤立波沿程波高衰减强度；Hi/H1表征了孤立波沿程衰减变化。

图9 不同入射波高、植物分布密度、分布宽度下孤立波相对波高沿程变化Fig. 9 Verification of relative wave height for different wave height,vegetation model densities and widths

图9(a)可以看出，在植物分布密度φ=0.044及宽度W=1.0 m条件下，随着孤立波波高H增大，波浪水质点流速和加速度越大，与植物区相互作用，湍动耗散更为强烈，波能衰减越快，波浪经过植物区后，3种不同入射波高(H=0.04、0.05、0.06 m)下，孤立波沿程波高衰减强度H5/H1分别为0.69、0.65、0.62。图9(b)可以看出，在入射波高H=0.05 m及植物分布长度W=1.0 m条件下，孤立波在植物模型前的壅高值随着植物分布密度φ的增大而增大，其中在φ=0.087时，壅高值最大增量为28%。当分布密度φ从0.044增加至0.087时，植物带沿程波高衰减趋势发生改变，植物带消波存在明显的边界效应，即植物带波能衰减更集中于植物带前半部分。3种不同植物分布密度(φ=0.044、0.062、0.087)下，孤立波沿程波高衰减强度H5/H1分别为0.65、0.57、0.47。图9(c)可以看出，在入射波高H=0.05 m及植物分布密度φ=0.044条件下，随着植物区分布宽度W的增加，波能衰减更快。3种不同植物区分布宽度(W=0.5 、0.8 、1.0 m)下，孤立波沿程波高衰减强度H5/H1分别为0.78、0.70、0.65。波浪经过植物区后，由于海堤的阻水效应，波高又逐渐增大。波浪壅高值对植物区分布宽度的变化并不敏感，相较于植物分布密度，植物分布宽度对孤立波在植物区的波能衰减率影响并不大，这一结论，对海啸减灾具有重要的借鉴意义。

4.3 孤立波越浪水体特征分布

Van der Meer等[37]总结了大量的试验结果，认为海堤不同位置遭受的破坏难易程度不同，进一步研究越浪流特征参数的空间分布尤为重要。为此，需要先定义两个变量，堤顶流厚度h(x)指在一个波浪完成越浪过程中经过堤顶某断面处出现的水流最大厚度。堤顶流速度V(x)指在一个波浪完成越浪过程中经过堤顶某断面处出现的最大水平流速[11]。堤顶流厚度及速度定义具体如图10所示。

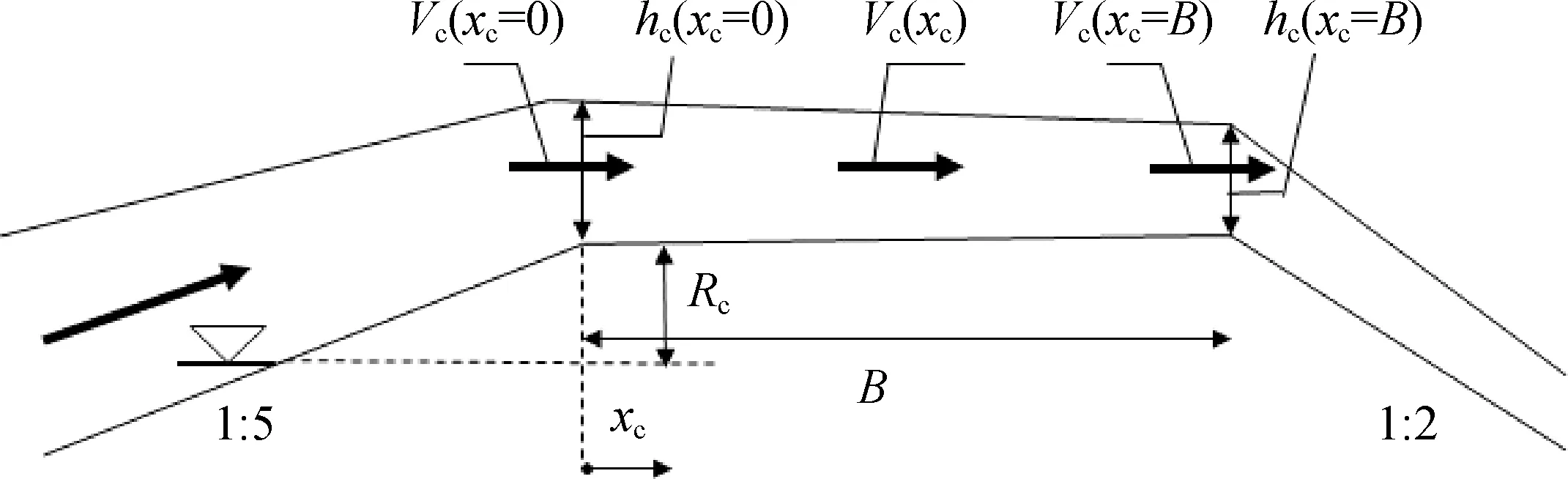
图10 堤顶越浪流厚度及速度定义Fig. 10 The definition of overtopping layer thickness and flow velocity on the crest

图11表示工况10条件下，海堤位置处不同时刻的速度云图。从t=15.30 s的速度云图可以看出，孤立波到达前坡时，发生浅水变形，波高增大，波形前倾且变得尖陡，波峰前方水质点流速方向为右上方，波峰后方水质点流速方向为右下方。t=15.75 s时波形变为拥有水舌前缘的水体，水舌前缘流速最大，且流速方向逐渐与前坡方向平行，之后水体达到堤顶，开始发生越浪现象。t=16.00 s时，水体厚度在堤顶前缘部位达到最大，随后沿着堤顶方向逐渐减小，呈现一定的规律，将在4.4节进行详细分析。水舌前缘流速始终保持最大，离水舌前缘距离越远，水流流速越小，流速方向始终保持与堤顶平行，在这一过程中，前坡开始有水体回落，但速度较小。t=16.35 s时，水舌越过堤顶达到后坡，堤顶上的水体厚度不再呈现前小后大的非均匀分布，而是逐渐呈现均匀分布，水体厚度逐渐保持一致。水体在堤顶前缘附近流速为0，左侧水体开始回落，且流速较大，导致水位下降并逐渐低于平均水位，右侧水体继续传递达到后坡，并与后坡水体相互作用，发生湍动耗散，从而完成整个越浪过程。

图11 工况10情况下不同时刻速度云图Fig.11 Snapshots of velocity contour of water body at different time instances in case 10

4.4 植物影响下相对堤顶流厚度分布规律

为了分析数值模拟结果，选取海堤堤顶等距分布的10个断面，输出这些断面越浪流的水流厚度及流速，用堤顶前缘处厚度hc(xc=0)和速度Vc(xc=0)进行无量纲化分析，考察其空间分布规律。所有工况下堤顶流厚度均沿程减小，但是在不同波高、不同植物分布密度及宽度下，堤顶流厚度分布又呈现不同的衰减规律。由于参数的无量纲化，堤顶前缘水流厚度hc(xc=0)随波浪非线性H/h、植物分布密度φ、植物分布宽度W改变的变化趋势不能得到体现，因此，将有量纲的数据列于表3。从表3可以看出，不同H/h、φ、W下堤顶前缘水流厚度具有明显单调的变化趋势，即堤顶前缘水流厚度随着波高的增大而增大，随着植物分布密度φ和植物分布宽度W的增大而减小。

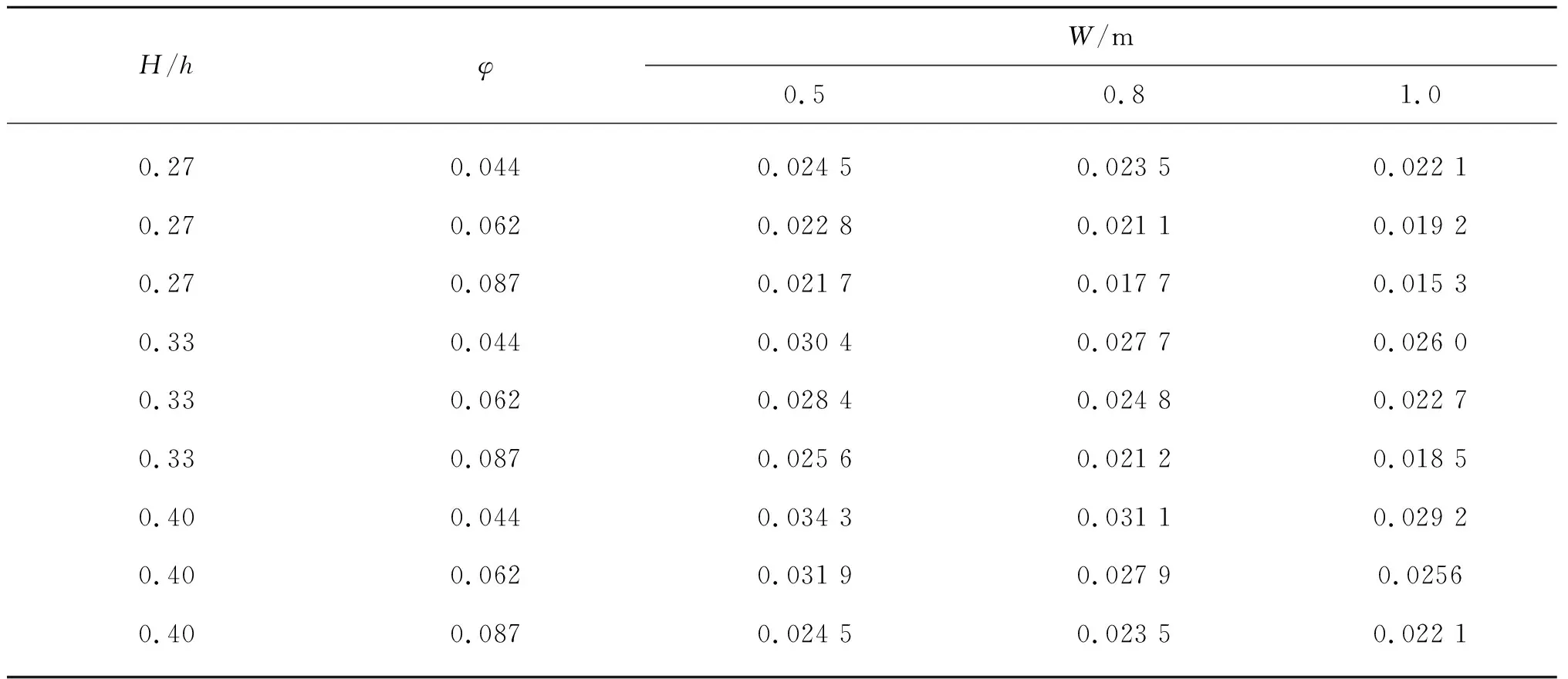
表3 堤顶前缘水流厚度数据Tab. 3 Date of overtopping layer thickness on the seaside of the crest (m)

图12表示在H/h=0.27、0.33、0.40，W=1.0 m时相对堤顶流厚度随植物分布密度φ的变化情况，其中φ、W=0代表无植物情况。当波浪非线性H/h=0.27时，在堤顶前段，植物分布密度越大，相对堤顶流厚度沿程减小的越快，在堤顶中段，植物分布密度对相对堤顶流厚度沿程变化没有太大影响，在堤顶后段，相对堤顶流厚度变化则呈现与前段相反的规律，即植物分布密度越大，相对堤顶流厚度沿程减小的越慢；当波浪非线性H/h=0.33时，相对堤顶流变化规律与H/h=0.27时相同，但在堤顶后段，相对堤顶流厚度沿程变化规律开始趋于相同，不同植物分布密度下(φ=0、0.044、0.062、0.087)，堤顶后缘(堤顶与后坡交界处)的相对堤顶流厚度分别为0.48、0.51、0.53、0.57；当波浪非线性H/h=0.40时，在堤顶前段，植物分布密度对相对堤顶流厚度影响进一步增大，在堤顶后段，不同植物分布密度下(φ=0、 0.044、0.062、 0.087)，堤顶后缘的相对堤顶流厚度分别为0.51、0.50、0.51、0.54，相对堤顶流厚度在堤顶后段沿程变化基本趋于相同。对比不同的波浪入射情况，随着波浪非线性的增强，在海堤堤顶前段，植物分布密度对相对堤顶流厚度沿程变化影响越来越大，植物分布密度越大，相对堤顶流厚度沿程减小的越快；在堤顶后段，植物分布密度对相对堤顶流厚度沿程变化影响越来越小，不同分布密度下，相对堤顶流厚度沿程变化趋近相同，且堤顶后缘的水流厚度约为堤顶前缘的二分之一。

图12 W=1.0 m时相对堤顶流厚度沿堤顶分布Fig. 12 Distribution of relative overtopping layer thickness on the crest for W=1.0 m

图13表示在H/h=0.27、0.33、0.40，φ=0.044时相对堤顶流厚度随植物分布宽度W的变化情况。与植物分布密度φ对相对堤顶流厚度影响相类似，植物分布宽度W的变化，主要影响堤顶前半段的相对堤顶流厚度的沿程变化，而堤顶后半段，相对堤顶流厚度沿程变化逐渐趋于一致，这种变化规律在波浪非线性较大时尤为明显。这是因为无论是植物分布密度φ还是植物分布长度W，其本质均表现为对孤立波沿程衰减作用，相对堤顶流沿程变化规律主要取决于波浪经过植物衰减作用后透射波高的大小。

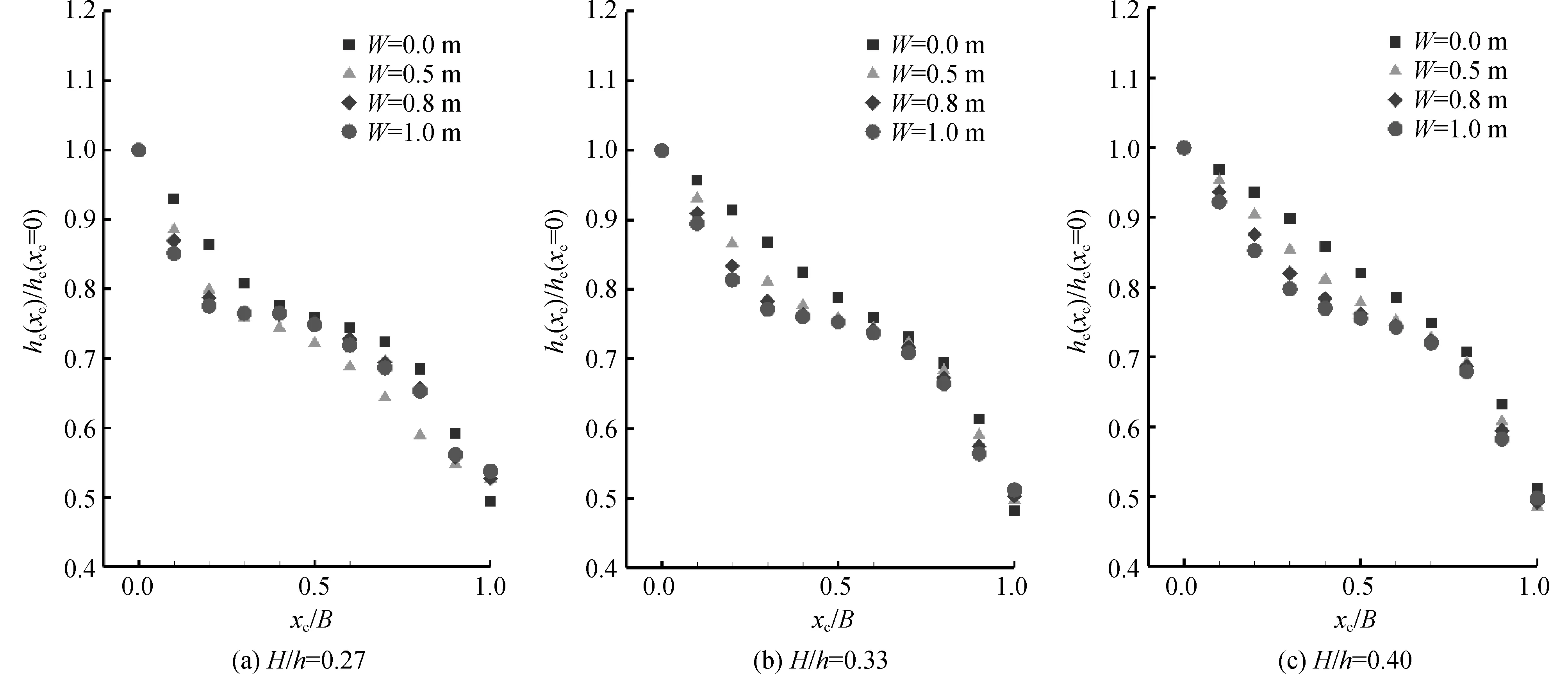
图13 φ=0.044时相对堤顶流厚度沿堤顶分布Fig. 13 Distribution of relative overtopping layer thickness on the crest for φ=0.044

4.5 植物影响下相对堤顶流速度分布规律

由于参数的无量纲化，堤顶前缘水流速度Vc(xc=0)随波浪非线性H/h、植物分布密度φ、植物分布宽度W的改变而变化的趋势不能得到体现，因此，将有量纲的数据列于表4。从表4可以看出，不同H/h、φ、W下堤顶前缘水流速度具有明显单调的变化趋势，即堤顶前缘水流速度随着波高的增大而增大，随着植物分布密度φ和植物分布宽度W的增大而减小。

表4 堤顶前缘水流速度数据Tab. 4 Date of overtopping flow velocity on the seaside of the crest (m/s)

所有工况堤顶流速度均沿程增大，且最重要的一个特征为堤顶流在堤顶后缘处速度都会突增，越浪水体内最大速度保持在堤顶后缘处。前人试验研究也发现过堤顶与后坡连接处最先产生侵蚀现象，可见，堤顶后缘在越浪流中是最需加固的部位。

图14表示在H/h=0.27、0.33、0.40，W=1.0 m时相对堤顶流速度随植物分布密度φ的变化情况，其中φ、W=0代表无植物情况。当波浪非线性H/h=0.27时，相对堤顶流速度沿程增加程度小于无植物情况，植物分布密度越大，相对堤顶流速度增加的越慢。其中当φ=0.044时，相对堤顶流速度沿程增加趋势与无植物情况相同；当波浪非线性H/h=0.33时，相对堤顶流速度沿程增加程度略大于无植物情况，但沿程变化趋势基本相同；当波浪非线性H/h=0.40时，相对堤顶流速度沿程增加程度大于无植物情况，且3种不同植物密度下，相对堤顶流速度沿程变化趋势基本完全相同。值得注意的是，在有植物分布情况下，堤顶后缘相对堤顶流速度均大于无植物情况，这就意味着尽管植物存在使得堤顶前缘流速减小，但堤顶后缘流速仍然有可能增加，从而导致海堤失稳破坏。对比3种不同入射波情况，随着波浪非线性增大，有植物情况下的相对堤顶流速度沿程增加程度大于无植物情况，但植物分布密度对其影响越来越小，不同植物分布密度下，相对堤顶流速度沿程变化趋于相同，且堤顶后缘的水流速度约为堤顶前缘的1.6倍。图15表示在H/h=0.27、0.33、0.40，φ=0.044时相对堤顶流速度随植物分布宽度W的变化情况。与植物分布密度φ对相对堤顶流速度影响相类似，植物分布宽度W在波浪非线性比较大时，有植物情况下的相对堤顶流速度沿程增加速度大于无植物情况，且植物分布宽度W对其沿程变化趋势影响较小。

图14 W=1.0 m时相对堤顶流速度沿堤顶分布Fig. 14 Distribution of relative overtopping flow velocity on the crest for W=1.0 m

5 结 语

采用非静压数值模型NHWAVE开展了非淹没刚性植物对海啸波作用下海堤水动力特性影响的数值模拟。通过与Huang等[34]和Hunt[36]的试验数据进行对比验证数值模型计算的可靠性。通过合理设置算例，研究了不同入射波条件和植物分布条件下沿程波形、波高变化以及堤顶流厚度与流速的空间分布规律，通过对计算结果分析，主要结论总结如下：

1) 随着植物分布密度和宽度增大，波能衰减增大，在波浪非线性较大时，植物消波具有明显的边界效应。孤立波在植物模型前的壅高值随着植物分布密度的增大而增大，但对植物分布宽度的变化并不敏感。

2) 不同H/h、φ、W下堤顶前缘水流厚度具有明显单调的变化趋势，即堤顶前缘水流厚度随着入射波高的增大而增大，随着植物分布密度和分布宽度的增大而减小。随着入射波非线性的增强，植物分布密度对堤顶前半段相对堤顶流厚度分布影响越来越大，对堤顶后半段影响越来越小，且堤顶后缘的水流厚度约为堤顶前缘的二分之一。

3)堤顶流最大速度保持在堤顶后缘处。不同H/h、φ、W下堤顶前缘水流速度具有明显单调的变化趋势，即堤顶前缘水流流速随着波高的增大而增大，随着植物分布密度和分布宽度的增大而减小。植物分布密度和宽度在波浪非线性较小时对相对堤顶流速度空间分布影响较大，波浪非线性较大情况下，植物对相对堤顶流速度空间分布几乎没有影响，但相对堤顶流速度增加程度均大于无植物情况，且堤顶后缘水流速度约为堤顶前缘的1.6倍。