带纵摇前墙的新型振荡水柱式波浪能装置转换效率以及水动力性能数值研究

任 翔，邓争志，程鹏达

(1. 浙江大学 海洋学院，浙江 舟山 316021； 2. 中国科学院 力学研究所，北京 100190)

随着对海洋能源需求的不断增加，从海洋中提取能源的研究也在逐步展开。波浪能作为海洋能源中最重要的能源之一，其开发与利用对缓解能源危机、减少环境污染具有重要意义。因此，学者提出了各种波能转换装置[1]，而其中振荡水柱式波浪能转换(OWC)装置因其维护简单、使用寿命长[2-3]，是目前应用最广泛的波能转换装置之一。在过去的几年中，为了提高OWC装置的效率，学者对OWC装置的形态进行了研究。

最初，学者提出了单OWC装置的概念，并从理论、试验和数值模拟三个方面进行了研究。OWC装置的理论最早是由Evans[4]和Falnes[5]提出的，他们在线性波理论的框架内将内部自由表面位移简化为一个无重力的活塞运动。Evans等[6]以经典线性波理论为基础，推导了压力分布均匀的振荡系统能量吸收效率的解析表达式。Sarmento等[7]根据线性波理论，对任意恒定深度水中的振荡水柱波能装置进行了二维分析。Rezanejad等[8]在线性波理论下分析了阶梯式地形在提高近岸OWC装置效率方面的作用。与此同时，人们也开始对OWC装置进行试验研究。Britomelo等[9]通过物理试验，研究了基于线性波理论的三维辐射衍射边界元程序在沿岸OWC装置波浪发电厂的适用性。Ashiln等[10]通过物理试验探索在规则波和随机波作用下，4个不同地形条件(包括平底,圆底,斜度1∶1和斜度1∶5)对整个设备的水动力特征的影响。Ning等[11]通过物理试验研究了入射波振幅、气室宽度、前墙吃水、开口率、底坡等参数对OWC装置水动力效率的影响。Deng等[12]通过试验和数值模拟，研究了带水平底板的近岸振荡水柱式波浪能转换装置的水动力性能。Jeong等[13]在波浪水槽中研究了浮式OWC装置在不同波浪条件和几何参数下的水动力性能。学者同样也在数值模拟方面进行了研究。Lee等[14]利用三维辐射/衍射代码WAMIT分析了一种通用的OWC装置。基于水平集浸入边界法，Zhang等[15]提出了一种基于整体质量修正的两相水平集和浸入边界法的数值方法来模拟波浪与半浸没气室(OWC)的相互作用，并与试验结果进行了比较。Ketabdari等[16]基于线性波理论和势流理论在频域内对OWC装置的效率进行数值模拟分析。Deng等[17]从理论上探究了对于非对称近海静止OWC装置，在底部增设水平底板后的水动力性能，并发现其可以拓宽装置的高效频率带。

在对单OWC装置的各个参数有了一定结论后，考虑到实际工程中的应用，耦合OWC装置与防波堤的方案也被提出并进行了研究。Rapaka等[18]提出了将浮式防波堤和浮式OWC装置相结合的浮式多共振振荡水柱式波浪能装置的水动力特性，并讨论了无量纲化的波浪频率参数对运动响应和系泊力的影响。在此之后，Hong等[19]利用销接式浮式OWC装置作为防波堤来保护超长浮式结构(VLFS)，结果表明该结构可以显著降低VLFS的水弹性响应。国内由史宏达等[20]首次将OWC装置与沉箱防波堤相结合进行相关水动力参数的物理试验探究。随着研究的深入，He等[21]开始对桩基OWC型防波堤的水动力性能进行试验研究，探究了相对宽度、吃水深度和开口情况对OWC装置的反射、透射、能量耗散系数和压力脉动的影响。结果表明，桩基OWC型结构具有良好的水动力性能，且在利用波浪能方面颇具潜力。陈帆[22]采用物理模型试验方法对兼作OWC装置的双圆筒沉箱防波堤进行了研究。近期，Deng等[12]通过试验和数值模拟，研究了带水平底板的近岸OWC装置水动力性能，并发现设置相对较长的水平底板和较小的开孔率能够提升装置的能量转换效率和阻波性能。这些结果进一步证明了OWC装置的研究价值。

为了使OWC装置达到更高的效率，学者提出了双气室OWC装置来探究其是否具有更好的水动力性能。Rezanejad等[23]在线性波理论下分析了阶梯式底部的双气室OWC装置效率。研究表明，在阶梯式底部的条件下设置双气室OWC比设置单气室OWC可显著提高装置在较宽频率带内的性能。因为有足够的数据来证明双气室OWC装置的优异水动力性能，Elhanafi等[24]研究了各种双气室离岸式OWC装置的水动力性能，并通过数值模拟将结果与单腔OWC装置进行了对比，发现双腔装置的水动力性能表现更好。同时Ning等[25]提出了一种新型的双气室圆柱OWC装置，以有效地在深水中获取波能。Ning等[26]对双气室OWC装置的水动力性能进行了试验研究，重点研究了该装置的整体性能以及系统中两个子气室的各自性能，结果表明，与单OWC装置相比，双气室OWC装置的最大能量转换效率和高效频率带宽均有所提高。而后Wang等[27]基于OpenFOAM模拟了一个小型的双气室OWC装置，该系统由两个仅能上下移动的气室单元组成，并对其水动力性能进行了研究。

目前已有的研究大多基于结构固定的OWC装置。为了提高装置的整体水动力性能，新型气室宽度可变的OWC装置逐渐被开发。近期，为了减少波浪反射，提高波浪能提取的气动效率，Deng等[28]提出了带可平移前板的近岸式OWC装置。结果表明前板可移动的OWC装置比传统固定式OWC装置具有更高的能量转换效率。基于此，为了能够使更多能量进入气室内部，并且拓宽OWC装置的高效频率带，提出一种带纵摇前墙的OWC装置。为了获得更高的能量转换效率，通过改变前墙的各项参数和后墙的吃水，对整个系统的能量转换效率进行了数值研究。

1 数值方法

1.1 控制方程

采用基于OpenFOAM的第三方工具箱waves2Foam的求解器waveDyMFoam来求解雷诺时均N-S方程，其包括质量守恒方程和动量守恒方程，在笛卡尔坐标系下的控制方程为:

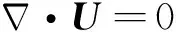
(1)

(2)

其中,U表示速度矢量,ρ是流体密度(空气和水),p*是似动力压力,g是重力加速度的向量,X是位移的向量,μeff是有效动态黏度(包括分子黏度和湍流黏性),σ是表面张力系数，κ是界面曲率。

该求解器使用流体体积法(VOF)[29]来确定交界面:

(3)

流体的性质(ρ和μ)可以用带α的函数来计算:

ρ=αρwater+(1-α)ρair

(4)

μ=αμwater+(1-α)μair

(5)

其中，ρwater和ρair分别为水和空气的密度，μwater和μair分别是水和空气的分子黏度。

1.2 数值计算

在求解控制方程过程中，采用有限体积法进行数值离散。过程中采用由Rhie[32]开发的配置网格方法，将计算域离散为一系列小单元，将所有的流场信息存储在每个单元的中心。OpenFOAM为控制方程中不同项的离散化方案和插值方法提供了多种选择。在模拟过程中，瞬态项采用隐式欧拉格式，对流项采用高斯有限线性1.0格式，黏性扩散项采用线性修正格式，其余项均采用线性插值格式。

OpenFOAM采用了PIMPLE求解算法，该算法由PISO(pressure implicit with splitting of operator)算法和SIMPLE(semi-implicit method for pressure linked equation)算法合并而成。采用SIMPLE算法将N-S方程与迭代过程相结合的方法，从速度场计算网格上的压力，用PISO算法对压力—速度项进行修正，默认欠松弛[33]。

1.3 造波和消波方法

OpenFOAM中的waves2Foam库为模拟规则波提供了多种预处理工具。文中选用二阶斯托克斯波来产生规则波。自由表面标高η和相关速度分量Ux、Uz可表示为:

(6)

(7)

为了保证数值模拟的准确性，在进口后部和出口前部分别设置了两个松弛区[34]。这样，波通过结构后所产生的反射波和透射波就不会产生二次反射波，从而满足开阔海域物理边界条件。

1.4 参数定义

研究的水动力参数包括反射系数Cr、透射系数Ct、能量耗散系数Cd和波能转换效率ξ。其中反射系数采用Goda两点法[35]将反射波与入射波分离，得出反射系数Cr为:

(8)

其中，Hr和Hi分别为反射波和入射波的波高。

透射系数Ct定义为:

(9)

其中，Ht为透射波的波高。

波能转换效率ξ是指该装置能转换的波浪能量大小，其值主要取决于水柱的起伏运动和气室内的空气压降。OWC装置提取的时均水动力能EOWC可由式(10)计算:

(10)

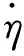
入射波功率可以表示为:

(11)

其中，ρ为水的密度，ω为角频率，k为波数，h为水的深度，Ai为振幅。因此，波能转换效率ξ的计算公式为:

(12)

根据波能守恒，能量耗散系数Cd量化了流体分离和涡脱落造成的能量损失比例，可以定义为:

(13)

2 模型验证

2.1 网格收敛性测试

在进行数值模拟之前，应对网格的收敛性进行验证，以确保网格已达到足够的精度，不会对试验结果产生影响。在研究中，使用了k-omega SST buoyance湍流模型。根据Deng等[36]的研究结果，网格设置应该保证每个波长至少设置100个网格，每个波高至少设置10个网格才会比较合理，同时建议每个周期至少设置1 000个时间步长。研究在保证网格分辨率正确设置的基础上通过库伦数Co和Coα来调节和控制时间步长，为变时间步长法，以提高数值精度，降低计算成本。

数值波槽长度如图1所示，长度L为35 m(约为最大波长的10倍)，水深h为0.45 m。数值模拟中设置了8个浪高仪G1～G8来测量不同位置的瞬时表面高程。浪高仪G1用来监测产生的入射波。G2～G4三个浪高仪利用Goda两点法[35]来分离入射波和反射波。浪高仪G5～G6用于监测气室中间的瞬时表面高度。两个浪高仪G7～G8位于OWC的后侧，用于计算透射波。利用两个压力探头S1～S2和9个速度探头S3～S11分别监测气室内外的气压降和气孔内的空气流速，并取平均值。

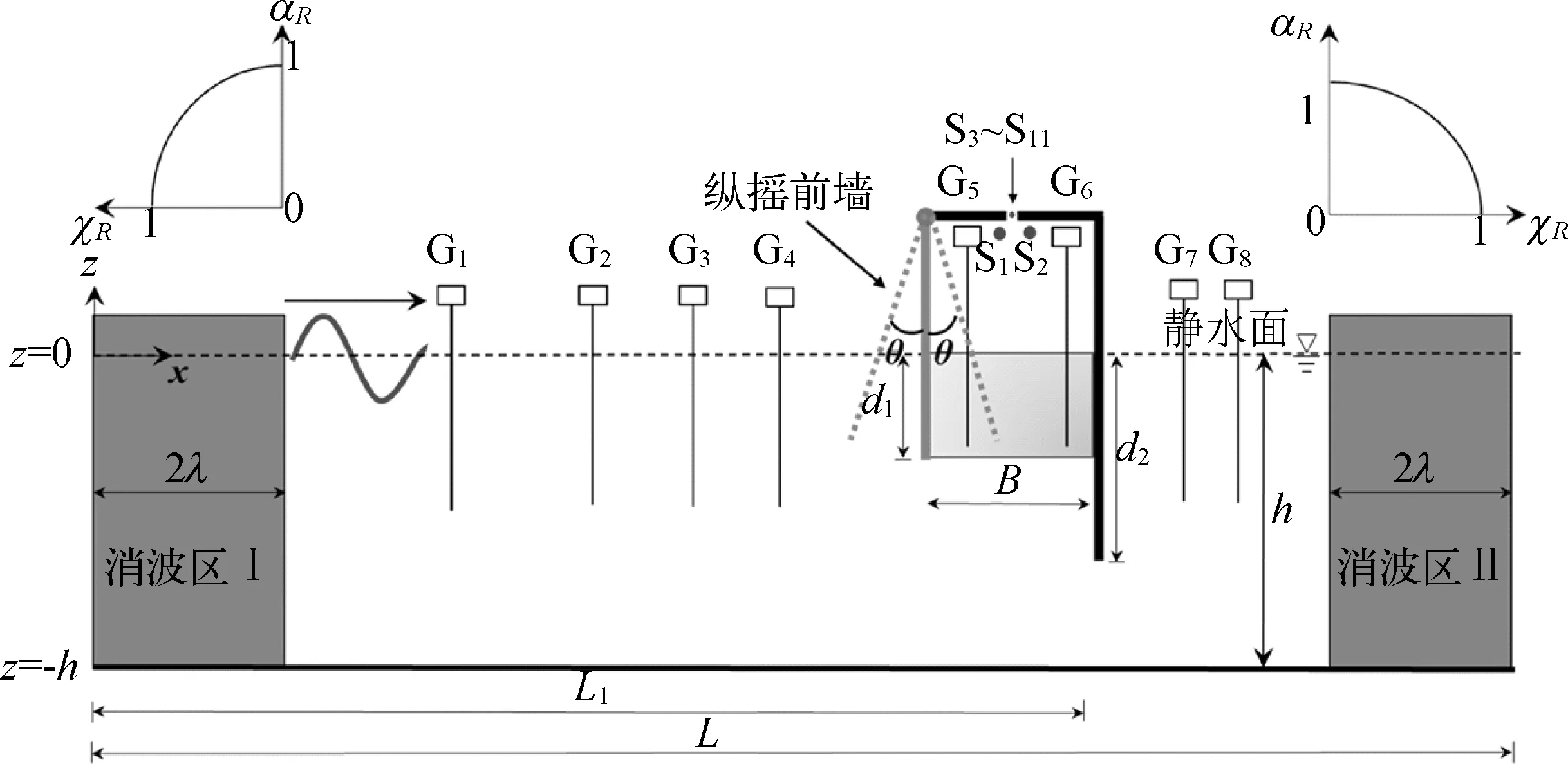
图1 数模布置示意Fig. 1 Sketch of the NWT

通过求解器waveDyMFoam-6DOF提供的扭转弹簧约束前板的旋转运动，其主要控制参数为刚度系数K，单位为Nm/rad。在固定旋转轴之后，前板相对初始时刻产生相对旋转角时，该弹簧会产生相反于旋转方向的约束力。为了更好地控制前板的运动，将弹簧的刚度系数无量纲化，定义其值为:

(14)

式中：m为前板质量，LB为前板长度。

而关于OpenFOAM数值波浪水槽的造波性能也早已得到学者的验证[37]。数模中入射波的波高和周期分别为Hi=0.01 m和T=1.8 s。OWC装置位于距造波边界17.1 m处。气室的宽度B为0.18 m,OWC的顶部开口率为1%，因此气孔的宽度为0.001 8 m。前板厚度为0.001 m，其余板厚度为0.01 m，前板长度为0.29 m，后板长度为0.45 m，前板吃水d1=0.10 m,d2=0.25 m。无量纲弹簧系数K设为0。考虑了细、中、粗三种不同空间分辨率的网格(图2)，因结构物附近可能产生涡而进行了加密，其中OWC装置周围加密后的最小网格尺寸分别为1、2、3 mm。

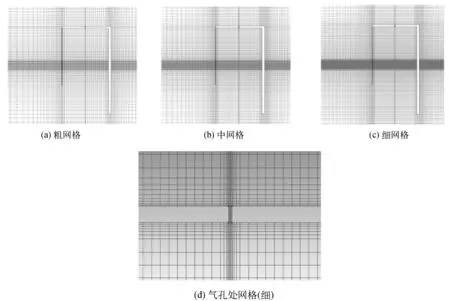
图2 三种不同分辨率的网格示意Fig. 2 Grid diagram of three different resolutions in convergence test

不同网格条件下OWC装置的空气流速和空气压降对比如图3所示。结果表明，不同网格条件下的模拟结果基本一致，最大误差不超过4%。从时间上看，若采用12核并行计算，细网格大约需要12 h，中网格大约需要8 h，粗网格大约需要6 h。因此，考虑到计算效率和精度，在接下来的数值模拟中选择使用中精度的网格。

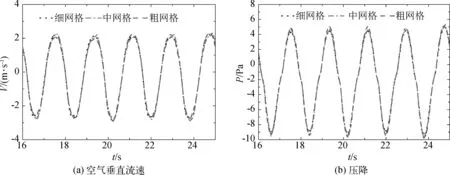
图3 不同网格分辨率下的数值收敛性结果Fig. 3 Numerical convergence study results for different grid resolutions

2.2 波浪能转换效率的验证

考虑到研究的重点是探索OWC装置的能量转换效率，在进行更多的数值模拟之前，需要验证计算出的波能转换效率的正确性。Elhanafi等[24]利用Star-CCM+软件研究了单气室离岸静止OWC装置的水动力性能。这里同样研究了单气室OWC，并将文中再现的结果与Elhanafi等[24]研究结果进行对比，结果如图4所示。可以看出，文中得到的波能转换效率数值结果与Elhanafi等[24]研究结果基本一致。因此，用这种方法来预测OWC装置的波能转换系数是相当可靠的。

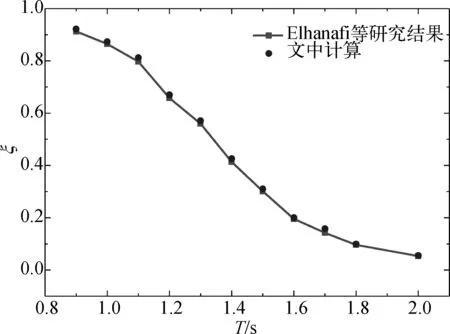
图4 波能转换效率ξ的结果验证Fig. 4 Comparison of wave energy conversion efficiency ξ between the previous and present results

2.3 动网格验证

研究中采用求解器waveDyMFoam-6DOF来求解动网格，因此对动网格的可靠性进行了验证。小球入水后的自由衰减情况[38]以及波浪作用下方箱的相对振幅[39]验证结果如图5和图6所示。可以看出，使用该方法的求解结果是可信赖的。

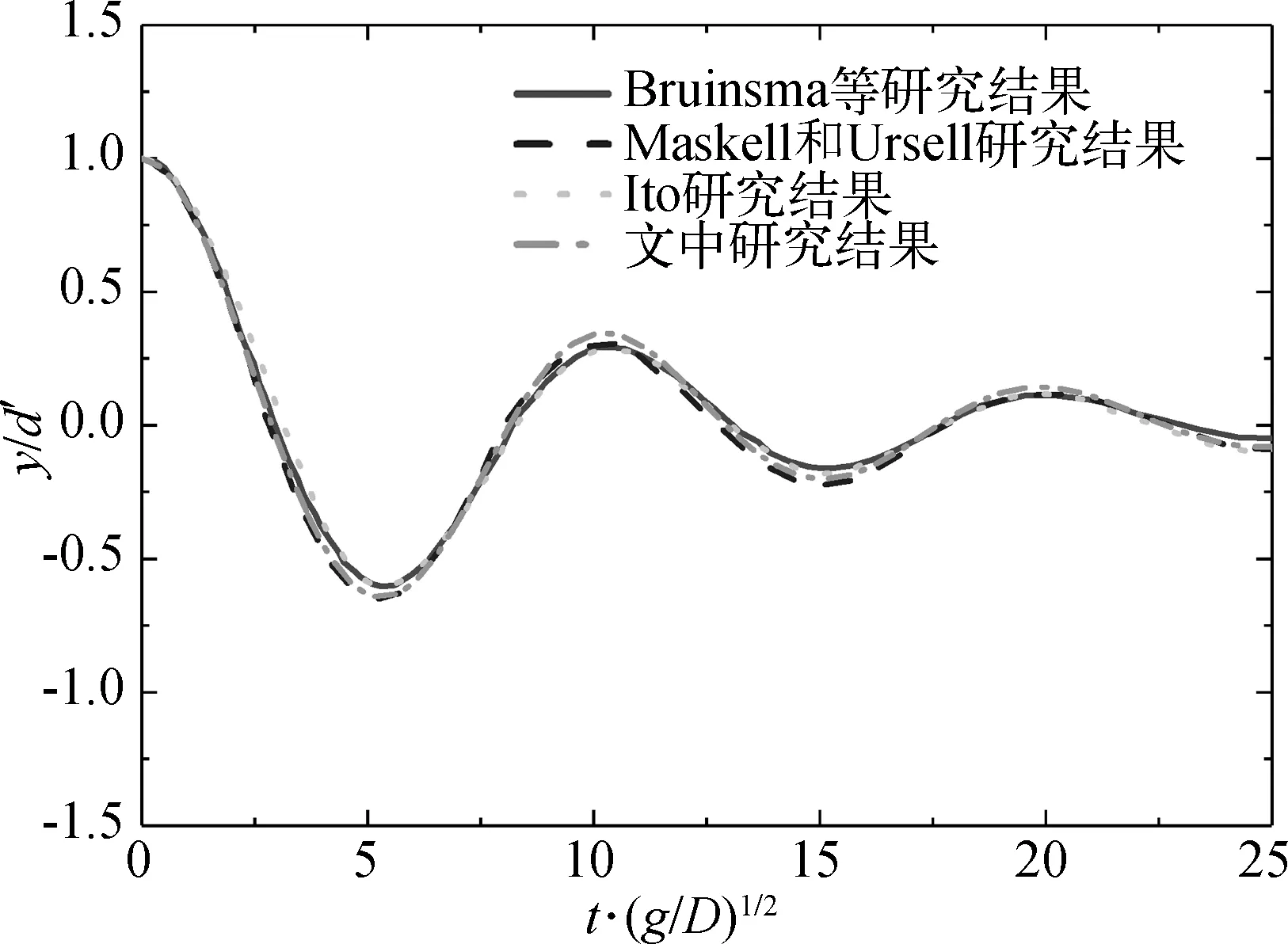
图5 小球入水自由衰减的结果验证Fig. 5 Comparison of vertical displacement of the heaving cylinder between the previous and present results

图6 方箱在波浪作用下相对振幅AH/A0的结果验证Fig. 6 Comparison of relative heave amplitude AH/A0 of box between the previous and present results

3 结果和讨论

在验证了数值模拟结果的可靠性后，通过数值模拟的方式研究带纵摇前墙OWC装置各参数对其整体水动力性能的影响。考虑的参数包括无量纲弹簧系数K(前板可旋转性)、前板吃水深度d1、前板密度ρ和后板吃水深度d2。除特别指明外，OWC装置的设置与上一节所使用的相同。

3.1 无量纲弹簧系数的影响

研究无量纲弹簧系数K对于OWC装置水动力性能的影响。模型的比尺拟定为1∶50，鉴于Elhanafi等[24]的研究中得出OWC装置气孔开口率为1%，气室宽度B为0.02 m左右可获得更宽的高效频率带，因此这里OWC气孔开口率ε固定为1%，气室宽度B固定为0.18 m，前板的吃水深度d1为0.1 m，后板的吃水深度d2为0.2 m，前板的密度ρ为1 500 kg/m3，波高H为0.01 m。无量纲弹簧系数K的数值设置为0、100、500、1 000、2 000、3 000、10 000和∞(在数模中设置前板为固定状态)，其中当K的值为0和∞时对应的分别是自由状态的可旋转前板和固定不可动的前板，而针对这两种情况细究了可旋转前板对反射系数Cr、透射系数Ct、能量耗散Cd和波能转换效率ξ的影响。

图7中显示了无量纲弹簧系数K对波能转换效率ξ的影响。值得注意的是，无量纲弹簧系数K对波能转换效率ξ的影响主要集中在短波区间。可以看出，当前板不受弹簧力约束时，装置的整体波能转换效率ξ保持在最高值，且在周期T=0.8 s时达到0.93，具有最宽的高效频率带。当入射波周期增大到1.6 s时，OWC装置的波能转换效率几乎不随无量纲弹簧系数K的变化而变化，随着入射波周期增大从0.12开始逐渐减小。当K值较小时(K≤500)，装置的整体波能转换效率曲线随着波长的增加而逐渐降低。然而,当K的值达到1 000或更高时,波能转换效率曲线随着波长增大先上升,然后下降，曲线中会出现一个峰值,而该峰值出现对应的周期(固有频率)随着K值的增大也将向短波区间移动。同时也可以看出随着无量纲系数K从0增加到∞，装置整体的波能转换效率先是下降而后有所上升。这一现象出现的主要原因可能是因为无量纲系数K的变化影响了前板的旋转幅度。当K值较小时，前板的运动幅度较大，改变了气室中水柱的共振频率，而在所研究的波浪频率中没能达到共振。然而，随着无量纲弹簧系数K的逐渐增大，前板的运动幅度开始减小，在一定的入射波条件下，两板之间的水柱产生共振，从而出现了波能转换效率ξ的峰值。而此时无量纲弹簧系数K进一步增大反而会增进振荡的稳定程度，减小弹簧晃动带来的能量消耗，从而整体的波能转换效率有所提升。一般来说，为了获得更高的波能转换效率ξ，更宽的高效频率带，应设置较小的无量纲弹簧系数K。

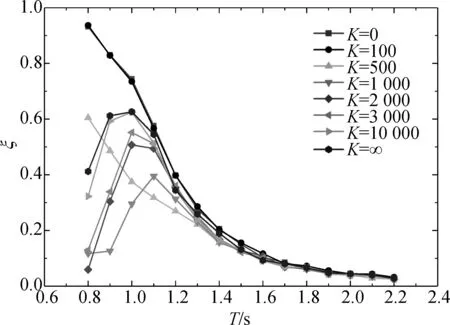
图7 无量纲弹簧系数K对能量转换效率ξ的影响Fig. 7 Effects of the non-dimensional spring coefficients K on the wave energy conversion efficiency ξ

从图8(a)的反射系数曲线中可以看出，对于一个固定的前板,反射系数Cr随着波周期变大首先从最大值约0.55开始减小，在波周期为1.0 s时降低到约0.23，而后随着波周期增大先是小幅度增加而后逐渐减小，最低在波周期为2.2 s时达到了0.20左右。而当前板可旋转时，在波周期为0.8 s时反射系数为最低值约0.13，随着周期增大反射系数逐渐增大到0.33左右，而后在波周期T=1.3 s时与固定前板的反射系数曲线变化趋于一致。当波浪周期T=0.8 s时，固定前板的反射系数达到峰值为0.55，而前板可旋转的反射系数确是最低值0.13。这是因为对于低周期波，固定的OWC装置并不能很好地吸收波能，而前板可旋转却使得更多的波能能够进入气室内部。总的来说,反射系数的差异主要体现在低周期区间，而这个现象可以由能量耗散系数与能量转换系数的差异证明(图8(c)和图8(d))。从图8(c)可以看出，前板是否可旋转在短波区间对OWC装置的能量耗散有很大的影响。这可能是因为能量耗散主要是前板底部的涡旋脱落造成,如图9所示，在短波情况下，对于纵摇前墙来说,前板底部产生的漩涡将远远小于固定的前板,所以能量的耗散相应减少了许多。对于中长波，大部分的能量都透过了结构，所以差别并不大。可旋转的前板由于减少了短波区间的能量耗散，因此有助于提高整个装置的能量转换效率，这点同样可由图8(d)所印证。固定的OWC装置能量转换效率随着波周期的变短先增大后减小，特别是当T=0.9 s和T=0.8 s时存在较大的差值，从0.6跌落到0.4，下降了33.3%。而当前板可旋转时，整个装置的能量转换效率随着波周期的变短呈现稳定的上升趋势，在T=0.8 s时达到峰值0.93，反而相较于T=0.9 s对应的0.83上升了12%，对比固定前板的0.4更是提升了133%。不同前板条件下，图8(c)和图8(d)的数据在波周期大于T=1.7 s后随着波周期的增加都趋于一致,这也反映出前板是否可旋转主要是对短周期入射波产生影响。而对于OWC装置而言，影响透射系数的关键因素是后板的吃水深度，因此前板是否可旋转并不会影响最终装置整体的透射系数，图8(b)验证了这一点。随着波长的增大，整个装置的透射系数呈增幅减小的上升趋势，这也说明该OWC装置只对短波具有良好的阻波效应。综合以上分析可知，前板可旋转可以有效提高整个装置在中短波区间的波能转换效率并且将反射系数控制在较小的阈值内。

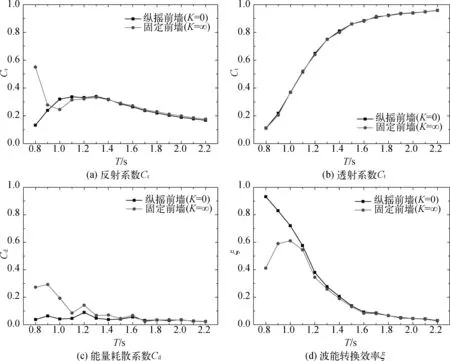
图8 前板是否可旋转的水动力系数对比Fig. 8 Comparison of the hydrodynamic coefficients for different front-walls

图9 结构物附近的涡分布Fig. 9 Vorticity distribution pattern in the vicinity of the structure

3.2 前板的密度和吃水深度的影响

探究前板的密度和吃水深度对于装置水动力性能的影响。试验中前板可以自由旋转(K值为0)，密度ρ0设置为1 500 kg/m3、2 000 kg/m3、2 500 kg/m3三组，吃水深度设置为0.08 m、0.10 m、0.12 m三组。其他参数与3.1节的设置相同。

考虑前板密度和吃水深度的变化(图10和图11)，最终的结果表明前板密度和吃水深度没有产生多少影响。在这4个水动力参数中，透射系数Ct本身就不太可能受到前板参数设置的变化影响。另一方面，造成这种现象的主要原因可能是前板的设置类型是可旋转薄板，其厚度仅为0.001 m。由于其质量相对较小，因此在研究中设置K值为0时前板密度改变未能产生本质的影响，前板的转动惯量相较于波浪力矩依旧是小数量级，主要还是随波浪振动而转动，而当K值为100未对波能转换效率产生影响也是一样的原因。而前板的吃水深度在前板转动较为剧烈的情况下(K值为0)，实际的有效吃水深度随波浪作用一直在改变，因此小范围的变化并没有对装置产生实质的影响。

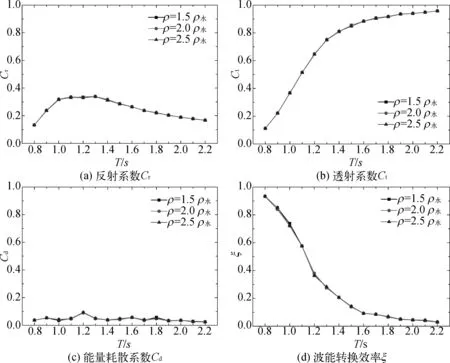
图10 不同前板密度条件下装置的水动力系数对比Fig. 10 Comparison of the hydrodynamic coefficients for different densities of the front-wall

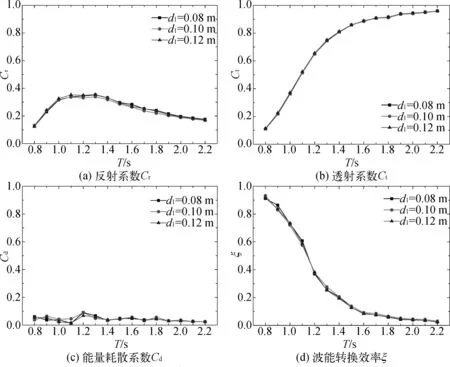
图11 不同前板吃水深度条件下装置的水动力系数对比Fig. 11 Comparison of the hydrodynamic coefficients for different draughts of the front-wall

3.3 后板吃水深度的影响

研究后板吃水深度对装置水动力性能的影响。在该节中前板的吃水深度为0.10 m，其余参数与3.1节相同。对后板吃水深度分别为d2=0.20 m、0.25 m、0.30 m的装置进行了探究。

图12(a)显示了不同后板吃水深度情况下反射系数Cr与波周期T的关系。由图12可以看出，无论后板吃水深度多大，反射系数Cr都先从最小值开始增大，然后随着波周期的增大而减小。当波浪周期T=0.8 s时，不同d2下的反射系数均在0.13左右为最低值。随着波周期的增加，反射系数逐步达到最大值，相对应的波周期也会随着后板吃水深度的增加而增加，当d2为0.20 m时其峰值对应的周期为T=1.1 s，而当d2为0.30 m时峰值周期增大到T=1.4 s。而装置整体的反射系数也随着d2的增大而逐渐增大，尤其在长波区间，后板吃水深度对反射系数的影响更大。Deng等[36]的研究也发现了类似的现象，原因是较大吃水深度的后板可以使更多的波能在自由表面附近集中。不同后板吃水深度情况下透射系数Ct与波周期T的关系如图12(b)所示。不同条件下装置整体的透射系数Ct都是随入射波长的增加而增大。当后板吃水深度从0.20 m增大到0.30 m时，透射系数达到0.6的临界周期从1.2 s左右增大到约1.4 s，可以看出随着后板吃水深度的增加，通过装置的波能减少，在更大的波周期范围内具有更好的阻波效果。而不同d2条件下的能量耗散曲线Cd差异不大(图12(c))，随着波周期的增长，均处于小于0.2的波动状态。仅当波周期大于1.8 s时，能量耗散系数Cd随后板吃水d2的增加而稍有增大。图12(d)给出了不同后板吃水深度下波能转换效率ξ与波周期T的关系。随着波周期的增加，能量转换效率逐渐降低，这表明装置对波能的高效提取主要集中在短波区间。后板吃水深度对波能转换效率的影响不可忽视。在T=1.0 s和T=1.6 s范围内，当d2从0.20 m增大到0.30 m后，能量转换效率均增大了约0.2。可见随着后板吃水深度的增加，波能转换效率有着显著提高。整体趋势中，不同后板吃水深度的波能转换效率都在波浪周期T=0.8 s时达到最大值约0.94，在波浪周期T=2.2 s时达到最小值约0.04。显然，后板的吃水深度将决定OWC装置内可以存储的能量大小，所以改变后板的吃水深度可以有效地改变装置的波能转换效率ξ。对于短波而言，OWC装置的能量转换效率已经达到上限，所以改变d2的影响不会太大，而对于长波，大部分能量不能保留在气室内部，都透射过装置，所以后板吃水深度的影响也不是很大。因此总体而言后板的吃水深度主要对中短波和中长波的波能转换效率有较大影响。

图12 不同后板吃水深度条件下装置的水动力系数对比Fig. 12 Comparison of the hydrodynamic coefficients for different draughts of the back-wall

4 结 语

对前薄板可旋转的新型振荡水柱式波浪能转换装置的水动力性能进行了数值研究。数值分析了该装置各参数对反射系数Cr、透射系数Ct、能量耗散系数Cd和波能转换效率ξ的影响。通过研究可以得出以下结论：

1) 通过降低整个装置的能量耗散率，纵摇前墙确实有助于提高整个装置的波能转换效率。改变无量纲弹簧系数K会对装置在中短波区间的波能转换效率产生很大的影响。当无量纲弹簧系数K较大时，波能转换效率曲线的峰值会出现在短波区间。当系数K为0时，装置的波能转换效率ξ最大，高效频率带最宽。

2) 当前板可旋转时，前板的密度和吃水深度对装置的水动力性能影响不大。

3) 后板的吃水深度d2对装置的水动力性能有一定的影响。增加后板的吃水深度可以有效提高中短波和中长波的波能转换效率，但对整体的能量耗散系数影响不大。透射系数随后板吃水深度的增加而减小，而反射系数随后板吃水深度的增加而增大。