基于海冰JH-2 模型的极地邮轮冰−船碰撞性能模拟分析

童宗鹏，叶林昌，夏兆旺，薛斌，曹锐

1 船舶与海洋工程动力系统国家工程实验室，上海 201108

2 上海船用柴油机研究所 动力装置事业部，上海 201108

3 江苏科技大学 能源与动力学院，江苏 镇江 212003

4 江苏南极机械有限公司 研发部，江苏 泰州 225400

0 引 言

极地邮轮在南极或北极航行时可能会与海冰发生碰撞，产生的冲击振动通过船体传递到船体结构、动力设备、船员工作舱室、居住舱室和旅客客舱，从而影响船舶安全性和乘客的舒适性体验[1]。因此，研究冰载荷对极地邮轮振动的影响，对于提高极地邮轮冰区航行舒适性和安全性具有重要意义[2-3]。实验研究极地邮轮与浮冰的碰撞问题成本高、周期长，而使用数值模拟方法研究极地邮轮冰−船碰撞具有成本低、周期短等优势，且数值模拟方法还可以模拟复杂海况[4-5]。

海冰模型是极地邮轮与冰碰撞分析的重要手段，在分析中，温度、围压和应变率都会对海冰的力学性质产生影响[6-8]。徐洪宇等[9]通过对海冰三轴压缩试验研究，发现海冰的抗压强度受围压和温度影响明显。因此，确定合适的海冰材料模型、获取准确的模型参数是极地邮轮冰区航行舒适性预报的关键因素。

目前，针对小型极地邮轮冰−船碰撞后的船舶安全性分析还不多。因此，为了明晰极地邮轮与海冰碰撞过程中船体的响应特性，本文将基于Johnson-Holmquist-2（JH-2）模型来描述海冰的力学性质，对极地邮轮冰−船碰撞过程的船体响应进行分析，用以为极地邮轮上的旅客舒适性及安全性分析奠定基础。

1 JH-2 模型的材料本构关系

JH-2 模型通常被用于模拟不同应变率的易碎材料的力学特性，如模拟分析玻璃、陶瓷和岩石等易碎材料的大变形破坏[10]。这些材料都具有较高的压缩强度以及较低的拉伸强度，在受到压力作用时会出现裂纹扩展现象，随着裂纹的增长而逐渐破坏。

1.1 JH-2 强度模型

JH-2 强度模型把材料的强度分为材料完整未破坏、材料开始破坏和材料完全破坏这3 种状态，且每个状态都由对应的状态方程来描述。其强度特性为：

1.2 JH-2 破坏模型

JH-2 破坏模型表征了材料破坏的非线性增长趋势，并使用式(4)描述材料的累积破坏模式。

1.3 JH-2 模型的压力状态方程

2 海冰JH-2 模型参数确定及其验证

已知海冰的弹性模量E=9 GPa，泊松比ν=0.33，剪切模量G=3.383 GPa，体积模量8.824 GPa，确定如下相关参数。

2.1 海 冰Hugoniot 弹 性 极 限 相 关 参 数 的确定

JH-2 模型的强度和压力参数都使用Hugoniot弹性极限（HEL）处对应的值进行归一化。因此，在确定其他参数之前，首先需要确定Hugoniot 弹性极限的相关参数值。海冰在−10 ℃时的主要参数如下[11]：Hugoniot 弹性极限0.161 3 GPa，冰内纵波波速3 866.0 m/s，剪切波速1 840.4 m/s。将参数代入Hugoniot 弹性极限处等效应力和静水压力的关系式[12]中，可得

2.2 海冰压力状态方程参数的确定

利用Hugoniot 方程可以推导出静水压力和体应变µ的关系式：

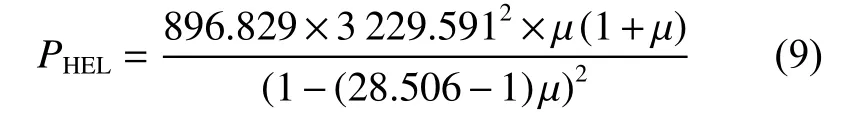
海冰的静水压力和体应变的关系如图1 所示，图中给出的是式(5) 中D=0 时压力状态方程的拟合结果。通过拟合，可确定K2=−1.625×1012Pa，K3=1.884×1014Pa。

2.3 海冰强度参数的确定

2.3.1 海冰未破坏时强度参数的确定

根据海冰三轴压缩的实验数据确定海冰的强度参数，再结合式(3) 得到海冰未破坏时的等效应力，由下式可求得不同围压下的最大静水压力。

最大拉伸静水压力可以由动态拉伸强度求得。已知海冰的拉伸强度范围为0.7～3.1 MPa，在5×10−3s−1应变率下，海冰动态拉伸强度为0.9 MPa。由下式分别求得海冰拉伸强度下的最大静水压力和等效应力。

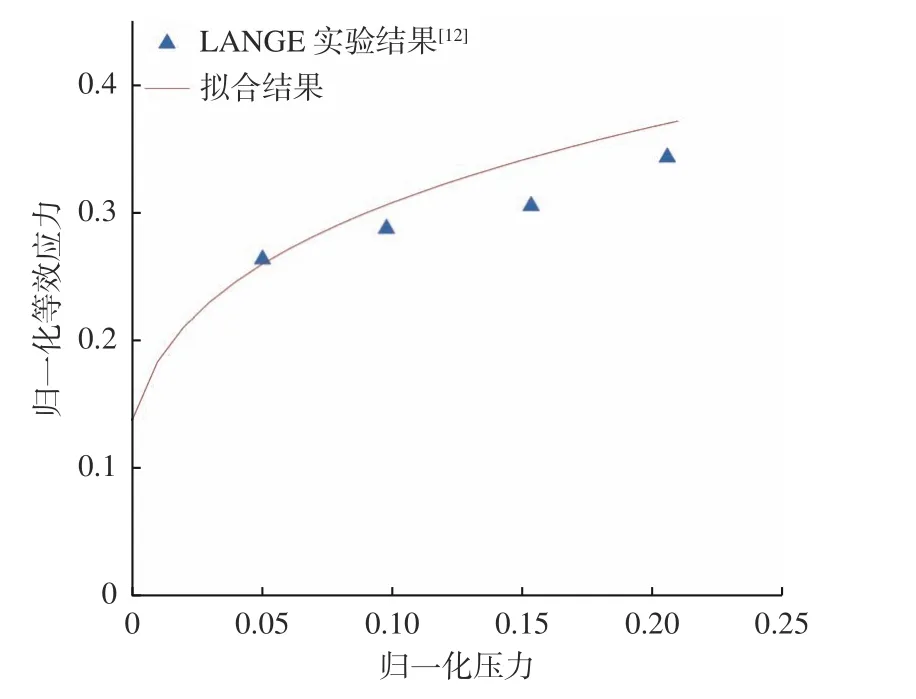
图2 归一化的等效应力与压力关系Fig. 2 Curve of normalized equivalent stress versus pressure

首先，由式（11）和式（12）求得的P和 σ进行归一化，再根据归一化等效应力与归一化压力的关系和海冰的动态拉伸强度，得到海冰的最大归一化压力为0.004 81，最大拉伸静水压力为0.6 MPa。

然后，确定JH-2 模型中的材料应变率系数C。材料抗压强度的增加主要是材料静水压力的增加所致，但应变率的影响也不容忽视。因此，需单独考虑应变率对海冰抗压强度的影响。不同应变率下单轴压缩强度和归一化等效应力如图3所示。拟合得到曲线的斜率后，即可求得C=0.041 40。在得出T∗，C和 ε˙∗的值后，可确定式(2)中A和N的值分别为0.711 50 和0.262 44。

根据上述海冰JH-2 模型参数的确定过程和结果，表1 列出了所有用于描述海冰JH-2 材料模型的参数及其数值。

2.3.2 海冰完全破坏时强度参数的确定

根据实验结果确定海冰的破坏强度可显著提高海冰模型的准确度，利用式(3) 拟合可以确定B=0.262 44，M=0.343 63。

2.4 海冰破坏参数的确定

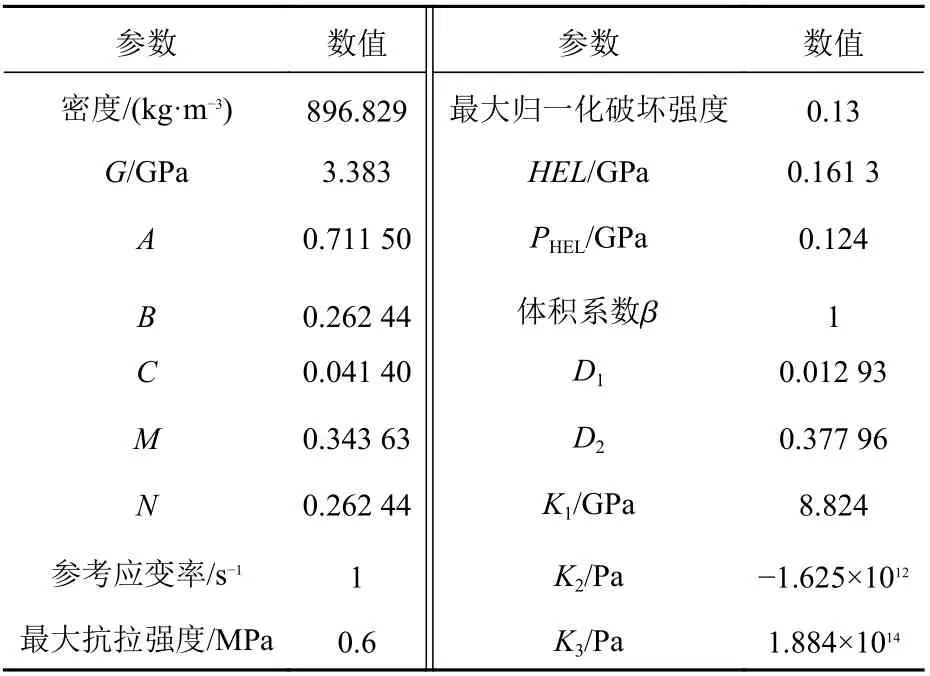
表1 海冰JH-2 模型的参数Table 1 Parameters used by the JH-2 sea ice model

材料损伤因子D描述了材料强度从未破坏到完全破坏的转变，体现了塑性材料从较大尺寸破坏到较小尺寸时的逐渐“软化”过程。材料未破坏时，D=0；达到完全破坏时，D=1。海冰破坏时的应变与归一化压力之间的关系如图4 所示。根据拟合结果，可以确定D1=0.012 93，D2=0.377 96。

图4 破坏应变与归一化压力的关系Fig. 4 Curve of damage strain versus normalized pressure

2.5 海冰JH-2 模型验证

陈晓东等[13]对渤海东北部海域的平整冰进行了单轴压缩试验，试样为横截面 50 mm×50 mm，高度107 mm 的长方体海冰。使用LS-DYNA 软件建立了海冰的单轴压缩模型。为了更好地模拟海冰的破坏过程，采用光滑粒子伽辽金（SPG）方法对海冰试样进行建模。该方法使用了基于应变的键失效机理来模拟材料的破坏现象，具有对材料使用的破坏准则不敏感、能考虑失效单元的自接触等优点。如图5 所示，模型底座和顶部的可移动钢板都被设置为刚体，底座为固定约束，对顶部钢板施加移动速度为0.8 mm/s 的压缩海冰，得到了如图6 所示的仿真与实验对比结果。

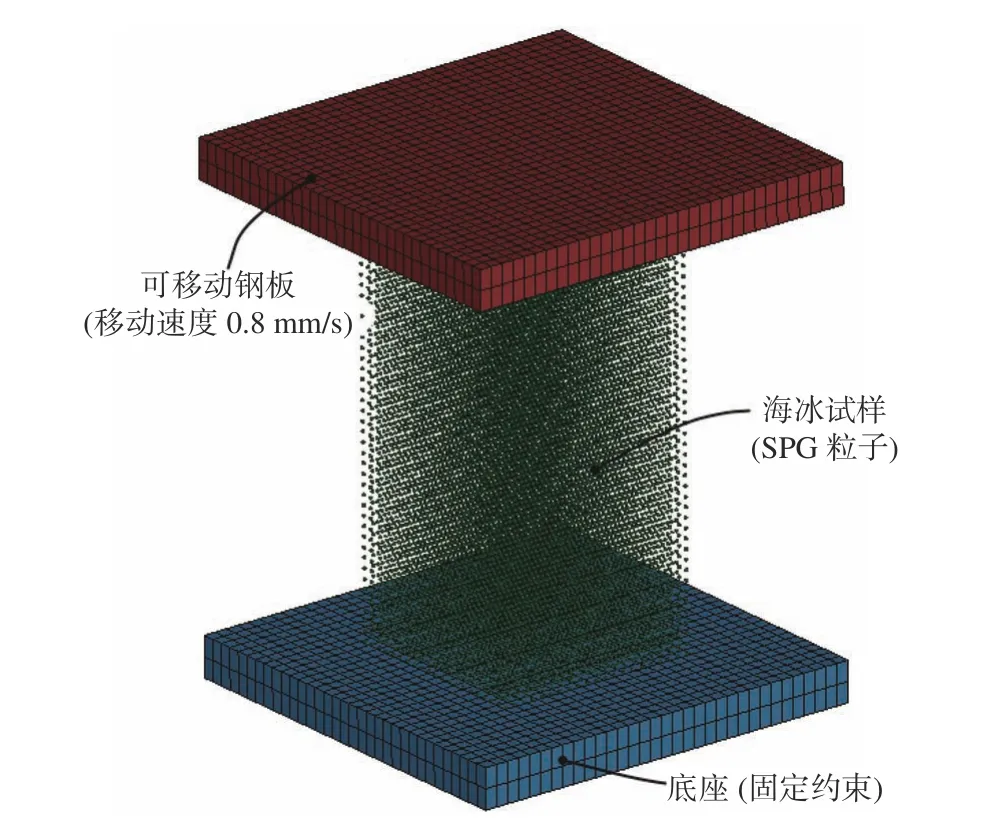
图5 海冰单轴压缩模型Fig. 5 Uniaxial compression model of sea ice

由图6 可知：最大加载力的数值模拟与实验的结果误差为7.8%，且数值模拟得到的海冰破坏时刻与实验结果的误差为4.5%；使用本文确定的海冰JH-2 模型可准确模拟出海冰破坏行为，其计算结果与实验结果为同一量级；实验结果显示了在加载过程中出现多次力卸载现象，这是因为实验海冰样本表面未经过特别处理，与试验机接触面不能完全贴合而存在小缝隙，故海冰在加载中存在局部破裂，导致加载力出现卸载现象。

图6 数值模拟与实验结果对比Fig. 6 Comparison between simulation and experimental results

3 极地小型邮轮与冰碰撞过程分析

本文研究对象为极地小型邮轮，根据图纸资料，利用有限元软件对极地邮轮的各层甲板、舱壁和关键肋位进行网格划分，建立了极地邮轮的全船有限元模型。

3.1 海冰的SPG−FEM 耦合模型的建立

SPG 是一种基于残差的伽辽金无网格方法，适合用于分析弹性材料损伤的局部应变和延性断裂等材料穿孔破坏的问题。为了改善直接点积分技术的秩亏问题，SPG 方法使用了从位移平滑理论推导的基于惩罚函数的应变梯度稳定算子[14-15]，位移平滑函数表示为：

SPG 方法实现了基于应变的黏结破坏机制，可以捕获位移场中的不连续性。每当两个相邻粒子的平均有效塑性应变和相对拉伸值达到其各自的临界值时，便会认为它们在无网格相邻粒子搜索过程中是断开的。如下，对于一对节点K和J，SPG形状函数[16-17]，可以定义为：

有限元方法（FEM）使用单元删除法模拟材料的破坏现象，计算结果受单元删除标准的影响很大且不能很好地模拟实际材料的断裂破坏现象；而SPG 利用基于应变的键失效机理模拟材料破坏过程，该方法具有对材料使用的破坏准则不敏感、能考虑失效单元的自接触等优点，但SPG 法计算耗时很长。因此，本文采用了SPG-FEM 耦合模型，其既可以提高精度，又可以提高计算效率。为了准确模拟海冰与极地邮轮挤压过程中的破坏现象，与极地邮轮接触区域的海冰使用SPG法建模，远离接触区域的海冰使用FEM 建模。其中可能与极地邮轮发生接触的海冰都采用细化网格处理，远离接触区域的海冰使用过渡网格划分，SPG 与FEM 建模接触的区域使用网格共节点法进行耦合。平整海冰的耦合模型如图7 所示，尺寸为1 44.6 m×50 m×1.6 m。使用SPG 法建模的海冰面积2 160 m2，冰层厚度1.6 m，过渡区域面积100 m2，FEM 建模的海冰面积4 860 m2。

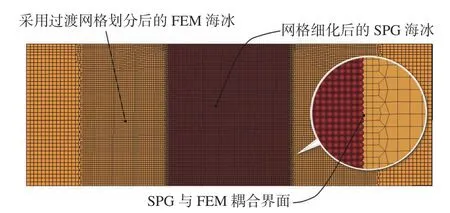
图7 平整海冰SPG−FEM 耦合模型Fig. 7 SPG-FEM coupled model of level sea ice

3.2 极地邮轮碰撞模型及结果分析

基于极地邮轮与平整冰碰撞的计算模型，对极地邮轮在冰区的连续破冰航行进行数值模拟，如图8 所示.。极地邮轮船长约104 m，船宽约18 m，总吨位约7 500 t，设计航速约15.5 kn，最大载员不少于200 人。以极地邮轮航速10.8 kn 为例，为了限制海冰的位移，对远离碰撞区域的海冰节点施加约束，主要约束其沿整体坐标系的平动自由度。

图8 极地邮轮与冰层碰撞分析模型Fig. 8 Collision analysis model for polar cruise vessel and sea ice

3.2.1 碰撞过程中海冰的破坏过程分析

由于极地邮轮具有极大的质量和撞击速度，使得发生海冰的破坏现象处于高应变率下，海冰在短时间内发生断裂和破坏。不同时刻下海冰的破坏和变形示意图如图9 所示，在碰撞过程中，海冰受到极地邮轮艏尖舱挤压碰撞而发生破坏。随着极地邮轮继续向前航行，海冰破坏范围进一步扩大，同时，破碎后的海冰被挤压到极地邮轮船体的两侧。此时，海冰没有出现大的裂纹扩展现象，因为海冰冰层较厚时（大于1 m），船体与海冰冰层发生挤压碰撞，海冰只会在与船艏直接接触的小范围内发生破坏，并不会在船艏周围及前方产生长距离的裂缝。

图9 不同时刻海冰的破坏变形Fig. 9 Failure and deformation of sea ice at different moments

3.2.2 碰撞过程中的冰载荷分析

在极地邮轮与平整海冰挤压碰撞的数值模拟中，分析了极地邮轮x,y,z这3 个方向的冰载荷，如图10 所示。

由图10 可见，极地邮轮与海冰碰撞过程中出现了多个冰载荷峰值，主要是由于碰撞过程中海冰的破碎导致极地邮轮与海冰之间的相互作用力在很短的时间内出现急剧的卸载和加载现象，完整海冰与邮轮接触时冰载荷慢慢增加到最大值，当海冰破碎时冰载荷迅速降低。此外，还可见：在y方向出现了负的冰载荷，这主要是因为y方向上极地邮轮船体两侧的冰层都会对船体产生作用力，所以在y方向上冰载荷有正、负之分；在y方向上的冰载荷比x方向上的冰载荷小，且船体两侧的冰载荷并非完全对称分布；在z方向上的冰载荷也较小，这主要是因为海冰冰层较厚，在z方向上船体与海冰也存在2 个作用区域，所以也出现了负值，但是碰撞过程中作用区域主要集中在一侧，从而导致冰载荷出现了明显的非对称分布。上述现象说明了海冰具有复杂多变的力学性质，也表明海冰模型对船−冰碰撞分析的重要性。

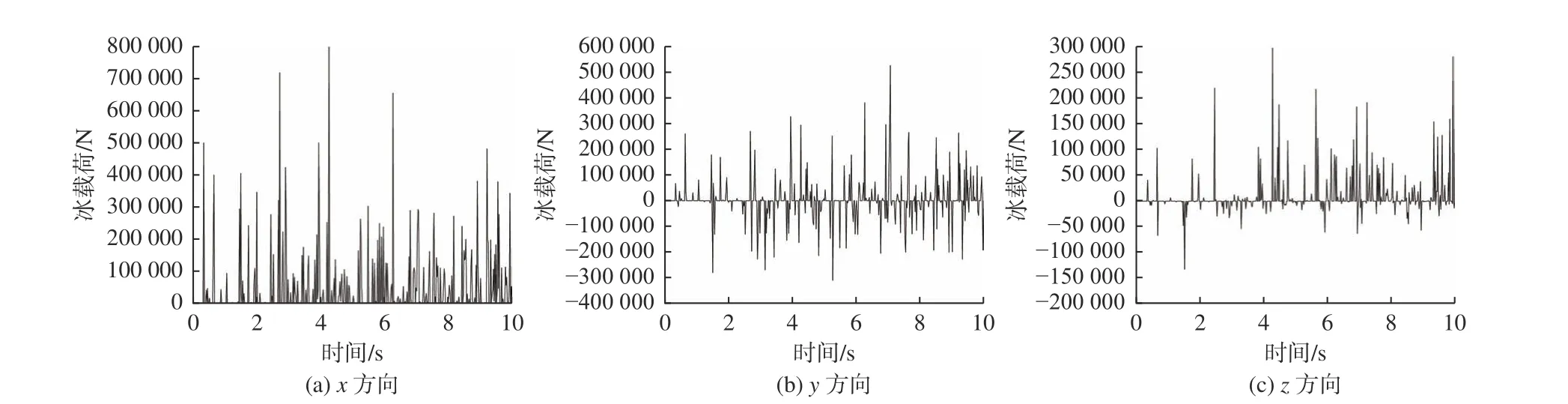
图10 邮轮与冰碰撞产生的冰载荷Fig. 10 Sea ice load caused by the collision of cruise vessel with sea ice

3.2.3 碰撞过程中海冰应力应变分析

对海冰进行应力分析主要是为了观察不同时刻海冰内力在宏观上的分布。而JH-2 材料模型和SPG 法中默认的破坏准则都是基于等效塑性应变，因此，通过观察应变云图可以确定海冰的破坏情况。海冰的应力云图和等效塑性应变云图如图11 和图12 所示。

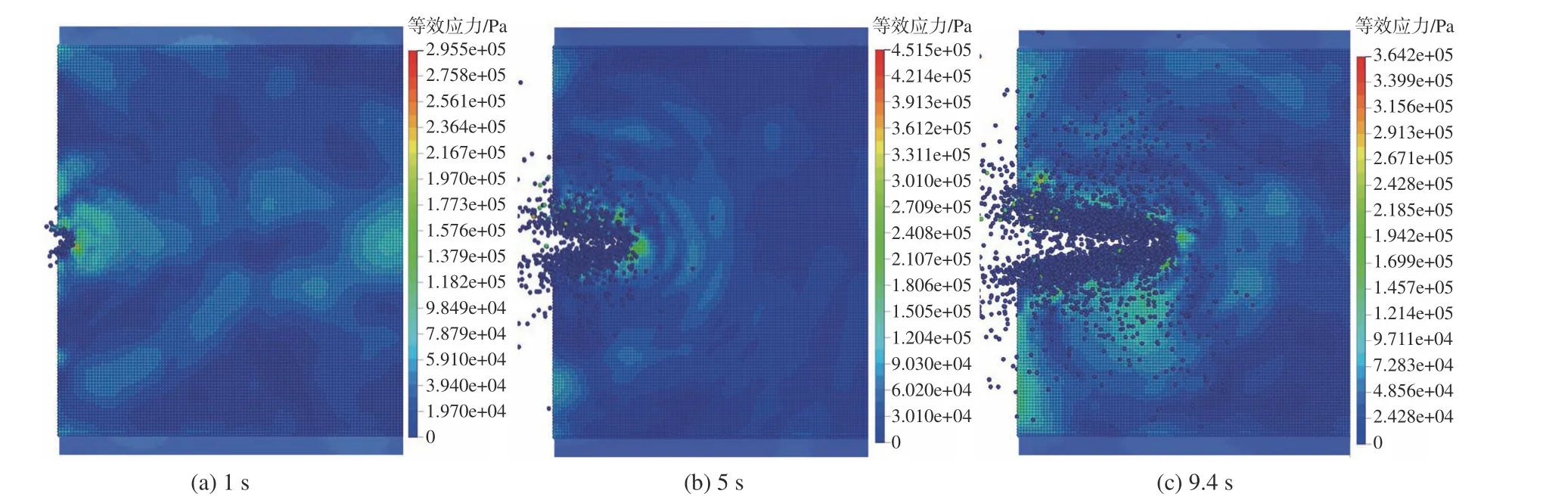
图11 碰撞过程中不同时刻海冰的等效应力分布图Fig. 11 Equivalent stress contour plot of sea ice in the collision process at different moments

图12 碰撞过程中不同时刻海冰的等效塑性应变分布图Fig. 12 Equivalent plastic strain contour plot of sea ice in the collision process at different moments

由图11 可见，因极地邮轮与海冰碰撞使海冰发生破坏，不同时刻海冰内应力的分布有明显的区别，说明海冰内应力状态不断发生变化，使得在不同时刻应力的大小也有区别，但最大应力位置都分布在靠近邮轮船体的区域内。

图12 中海冰的等效塑性最大应变位置都处于船体周围，说明这些位置的海冰发生了破坏变形，而远离碰撞区域海冰的等效塑性应变为0，这些区域的海冰在短时间内还不会发生破坏。从图12 (c)中还可以发现，在靠近极地邮轮船艏两侧的非直接碰撞区域的海冰也出现了局部应变，这说明随着极地邮轮深入海冰内，其与海冰的碰撞区域越来越大，此时，极地邮轮船体两侧的海冰将会出现破坏趋势，若极地邮轮继续向前航行，靠近船体两侧的海冰将发生破坏，而船艏正前方的海冰未出现这种局部应变，因此，随着极地邮轮的深入，船艏前方的海冰只会在直接接触区域发生破坏。

4 结 语

本文基于海冰JH-2 模型，利用SPG 法模拟海冰的破坏过程，分析了海冰各参数的物理意义及其确定方法，并对比了使用该模型得到的加载力数值模拟结果和实验结果。结果表明：海冰所受的加载力随着时间的变化而逐渐增加，在达到最大值后突然下降为0；最大加载力的数值模拟结果与实验结果误差为7.8%，且数值模拟得到的海冰破坏时刻与实验结果的误差为4.5%。

本文还采用SPG-FEM 耦合模型研究了极地邮轮与海冰碰撞时海冰的破坏过程，结合海冰的等效应力和等效塑性应变，研究了碰撞过程中海冰的破坏模式。结果表明：对于厚度为1.6 m 的海冰冰层，邮轮与冰层撞击过程中海冰冰层不会出现大的裂纹扩展现象，海冰只在与船艏直接接触的小范围内发生破坏，在船艏周围和前方没有产生长距离的裂缝；在靠近极地邮轮船艏两侧的非直接碰撞区域的海冰出现了局部应变，这说明随着极地邮轮深入海冰内，极地邮轮船体两侧的海冰将会出现破坏趋势，若极地邮轮继续向前航行，靠近船体两侧的海冰将会发生破坏，而在船艏正前方的海冰没有出现局部应变，表明船艏前方的海冰只会在直接接触区域发生破坏。