一种偏置集中力火箭舱体结构优化设计研究

王春林，张 游，赵学成，黄 帅，张欣耀

（1. 上海宇航系统工程研究所，上海，201108；2. 上海航天设备制造总厂有限公司，上海，200245）

0 引 言

随着中国探索太空的规模越来越大，对运载火箭的运载能力要求也越来越高。中国新一代运载火箭采用捆绑构型，即在火箭芯级四周捆绑一定数量的助推器，大幅提升了火箭的运载能力[1]。相对于单芯级火箭，捆绑构型的运载火箭结构受力也更加复杂，结构设计难度更大。通常需要在火箭捆绑点处布置特定结构以承受捆绑集中力，并对集中力进行扩散，在新一代大推力捆绑火箭设计中，对局部部位的捆绑支座、短壳等进行拓扑优化，取得了良好的减重效果[2～4]。结构拓扑优化技术作为一种新型优化方法，在航天领域复杂结构设计中得到了成功应用[5,6]。

根据某大型捆绑火箭结构构型和载荷条件，助推器捆绑点处受到偏置集中力，即集中力作用点延伸到火箭舱体侧壁外侧。采用多工况折衷规划理论，对舱体整体传力路径进行拓扑优化设计，获得一种偏置集中力舱体结构，解决了助推器捆绑点偏置集中力传递和扩散设计问题。

1 助推器偏置集中力舱体结构优化方法

1.1 拓扑优化设计流程

首先建立舱体三维设计模型，根据舱体的设计区域、载荷工况、边界条件建立有限元优化模型，采用拓扑优化方法获得舱体结构最优传力路径，再结合制造工艺，对拓扑优化结果进行工程化设计，并对结构进行有限元仿真分析，判定结构设计结果能否满足使用要求，若不满足，则分析原因重新对工程化设计进行修改，直至结构设计结果满足要求。拓扑优化设计流程如图1所示。

图1 拓扑优化流程Fig.1 The Flow Chart of Topology Optimization

1.2 拓扑优化模型的建立

在拓扑优化方法中，变密度法（Solid Isotropic Material with Penalization，SIMP）的拓扑优化理论是应用较为广泛的连续体结构优化理论[6,7]。变密度法通常以结构最小柔度为优化目标，假设材料弹性模量与其密度的关系为

式中ρe为单元的相对密度；p为惩罚因子；Ee(x)为单元材料弹性模量；E0为单元材料初始弹性模量。

根据某大型火箭助推器全任务剖面的使用要求，在火箭飞行中随着姿态、过载等不断变化，助推器捆绑点处受到集中力载荷的方向和大小也在变化，即助推器捆绑点需要承受多个载荷工况。根据拓扑优化理论，采用柔度最小化为结构优化目标，为实现多个工况下结构柔度最小，需要建立多目标优化模型。有中国学者采用柔度线性加权平均处理多目标优化[5,8]，该方法在面临非凸优化问题时不能保证获得Pareto最优解。而采用折衷规划理论可解决该优化问题，通过寻找多目标优化问题的折衷解，使得与每个目标函数最优解距离最小[9]，因此将上述多目标函数优化问题转化为单目标函数优化问题。优化模型还需要建立约束函数，除了拓扑优化中常用的体积约束外，偏置集中力舱段结构还需要满足结构变形约束、集中力扩散效率约束和结构应力约束。根据目标函数和优化约束，建立优化模型：

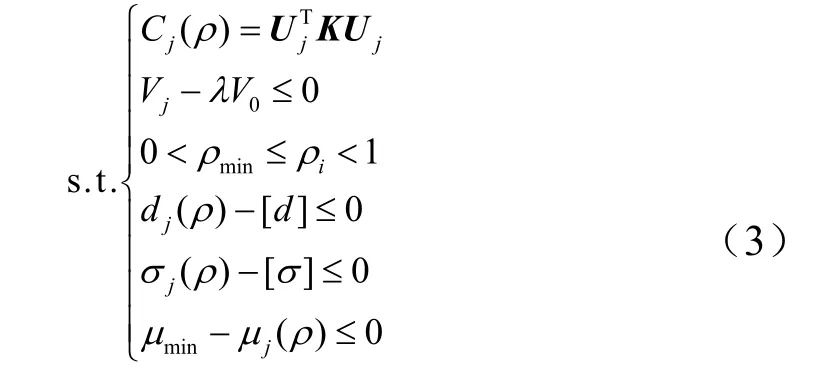
式中F(ρ)为多工况综合目标函数；ρ=(ρ1,…,ρn)T为单元设计变量，即相对密度；ηj为第j个工况权重系数；p为惩罚因子，p≥2；Cj(ρ)为第j个工况柔度目标函数；Cjmin为第j个工况柔度最小值；U为位移向量；K为结构刚度矩阵；Vj为拓扑优化后体积；V0为结构初始体积；λ为体积比；ρmin为设计变量下限取值；dj为第j工况下结构位移；[d]为结构许用位移；σj为第j工况下结构最大应力；[σ]为结构许用应力；μj为第j工况下集中力扩散系数；μmin为集中力扩散系数下限值。

2 助推器偏置集中力舱体结构优化设计

根据舱体外形建立初始设计模型，将捆绑点处凸台作为非设计区域，其余均为可设计区域，舱体底面一定区域圆环面设置固支边界条件，在捆绑点凸台处施加集中力。以多工况综合目标函数最小化为优化目标，开展舱段最优传力路径拓扑优化，优化模型如图2所示。

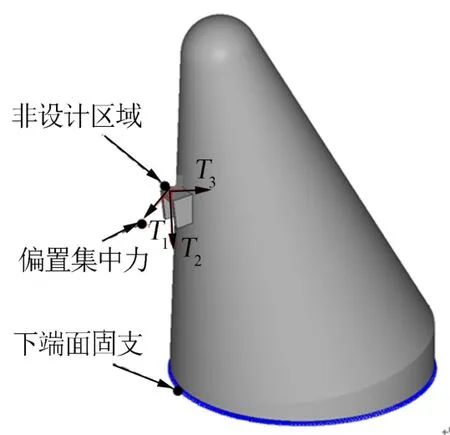
图2 舱体结构初始优化模型Fig.2 Initial Optimization Model of Cabin Structure

经过拓扑优化，结果如图3所示，对舱段整体材料分布规律分析，优化结果将偏置集中力分解为两部分进行传递，一部分为偏置集中力产生沿侧壁向下的轴力，优化结果采用变截面的轴力扩散结构进行传递。另一部分为偏置集中力产生的局部附加弯矩，该附加弯矩增加了局部结构受力复杂性，优化结果采用横向的弯矩平衡结构进行传递，由于弯矩平衡结构横贯整个舱段，获得力臂最大化，实现了平衡弯矩最优化。通过将偏置集中力产生的轴力和附加弯矩进行解耦，从而改善捆绑点处结构受力环境，降低局部结构应力，提高结构承载能力和结构效率。

图3 舱体结构拓扑优化结果Fig.3 Topology Optimization Results of Cabin Structure

根据拓扑优化结果，设计了一种“梁式”舱体结构：

a）偏置集中力产生的轴向力采用沿舱体侧壁周向扩散结构进行传递和扩散，扩散结构主要通过捆绑支座和放射筋壁板实现，如图4所示。

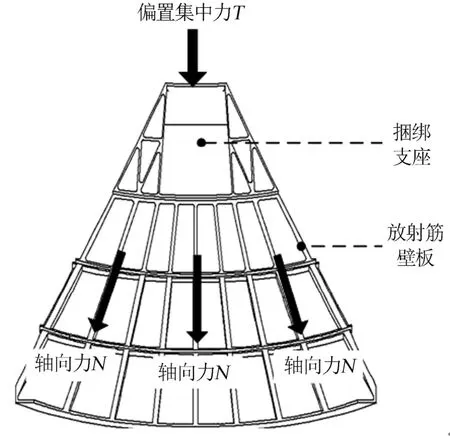
图4 轴力传递和扩散结构Fig.4 Axis Force Transfer and Diffusion of Structure

b）偏置集中力产生的附加弯矩采用一根横向贯穿舱段的大梁进行传递和平衡，大梁靠近捆绑点一侧受压，远离捆绑点一侧受拉，在大梁上形成平衡力矩用于平衡附加弯矩，如图5所示。

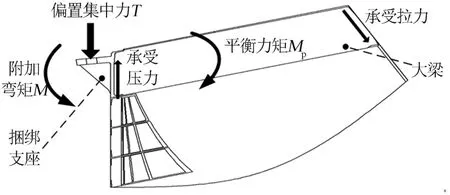
图5 附加弯矩传递和平衡结构Fig.5 Transfer and Balance of Additional Moment of Structure

3 强度仿真分析

为验证拓扑优化结果工程化设计的正确性，采用ABAQUS对结构进行有限元仿真。为了验证偏置集中力分解传递的正确性，分别针对“梁式”舱体构型和无大梁舱体构型的舱体结构进行建模计算，两种模型除有无大梁结构区别外，其余结构、载荷及边界条件相同，对舱体结构整体稳定性和结构应力强度进行仿真分析。分析结果如表1所示，相比无大梁舱体构型，“梁式”构型的轴压稳定性剩余强度系数提高了14.2%，结构承载能力有明显提高，而结构应力及变形位移均明显下降，大梁能够有效提升舱体整体结构刚度。结果证明针对偏置集中力舱体，采用轴向和横向分解传递的舱体传力路径优化设计结果正确有效。

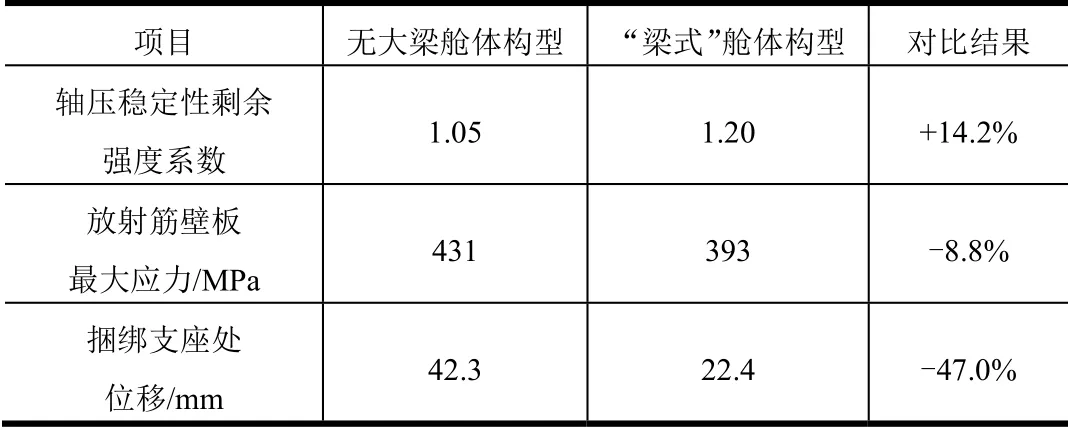
表1 两种舱体结构仿真结果Tab.1 Simulation Results of Two Cabin Structure Configurations

4 试验验证

为了验证结构设计合理性和仿真分析准确性，开展舱体结构偏置集中力工况下静力试验。试验时在捆绑支座处施加偏置集中力，舱体下端面固支，如图6所示。

图6 舱体轴压静力试验Fig.6 Static Test of Cabin Structure

试验载荷施加到111.6%倍设计载荷时达到加载设备极限，舱体结构完整未失稳破坏，结构整体稳定性剩余强度系数大于1.116，与仿真分析结果相吻合。对设计载荷下舱体上实际测点处的位移和应力与仿真分析结果进行对比，如表2所示，试验结果和仿真分析结果误差小于15%，验证了偏置集中力舱体结构优化设计正确性和仿真分析的准确性。

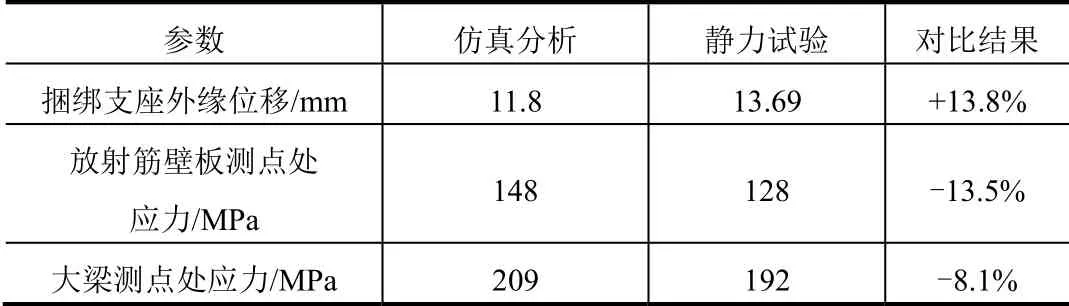
表2 舱体结构试验与仿真分析对比Tab.2 Comparison between Static Test and Simulation Analysis ofCabin Structure

5 结束语

本文针对运载火箭助推器舱体承受偏置集中力问题，开展舱体结构整体优化设计、仿真及试验研究。

提出了一种针对多工况多约束的舱体结构拓扑优化思路，采用折衷规划解决了舱体多工况优化问题。

针对助推器捆绑点偏置集中力传递和扩散设计问题，提出了一种 “梁式”舱体结构，对偏置集中力采用轴向和横向分解传递，经过仿真分析，相比无大梁的舱体结构，“梁式”舱体结构整体承载能力提高了14.2%。

“梁式”舱体结构通过了地面静力试验考核，验证了偏置集中力舱体结构优化设计的正确性，对后续其他火箭偏置集中力舱体结构研制具有参考意义。