基于发射约束的双曲线轨道运载能力计算方法研究
张博戎,王建明,李静琳,韩雪颖,周 敬
(1. 北京宇航系统工程研究所,北京,100076;2. 北京控制工程研究所,北京,100190)
0 引 言
对于需要进入地球双曲线轨道的发射任务,轨道全局设计与优化是其中的首要问题[1]。在这一类任务规划问题中,发射窗口和运载能力是关键的设计指标。
针对发射窗口选择问题,目前基于兰伯特(Lambert)问题快速求解算法,已经能够对多脉冲轨道转移问题进行建模,并结合多种优化方法寻优。特别是在简单的双脉冲直接转移问题中,利用Pork-Chop图方法能够直观展现发射窗口与速度增量之间的关系,以便任务规划选择[2]。
针对运载能力计算问题,目前主要研究方法是将速度机动转换为燃料质量消耗,从而将这一指标纳入全局优化。有学者在轨道优化中加入干重指标,为全局优化开辟了新的角度[3]。此外,也有学者基于火箭发射轨道特征,在不同发射射向和偏航情况下,定性分析了火箭有效载荷初始入轨质量变化规律[4],值得进一步研究其与出发轨道的匹配关系。
在选择发射窗口和计算运载能力过程中,应注意各项工程约束对于任务指标的影响。诸如火箭发射场大多处于固定地理位置,因此对于入轨停泊轨道的倾角范围具有限制。有学者在轨道全局优化中限定了赤纬(即地球赤道坐标系中一个点的纬度值,可理解为纬度在天球上的投影)或停泊轨道倾角范围[5~7],但单纯施加这一约束过于绝对,仍与实际发射情况有差异。再者,大多运载火箭末级可在停泊轨道上滑行的时间范围小,因此对入轨点存在约束。在此基础上,有学者研究了考虑射向和滑行时间约束的发射轨道匹配方法,并利用“赤纬-发射能量”图判断发射可行性[8],获得了更符合火箭实际发射能力的匹配规律,但是没有分析运载能力变化。
总的来讲,目前有关进入双曲线轨道的运载能力计算与发射窗口选择相结合的研究较少,而事实上这两部分指标是紧密相关的。发射能量较优的窗口未必能够实现最大运载能力,而若追求有效载荷质量尽可能增加,则有可能牺牲原窗口的优化指标。美国2018年利用宇宙神V运载火箭发射洞察号探测器,以北射向损失运载能力为代价,获得了更好的发射机会[9]。今后,随着进入双曲线轨道的任务逐步增多,将运载能力计算与发射窗口选择相结合具有理论上和工程上的研究价值。
进一步具体分析运载火箭发射中的各项约束条件,其中发射场纬度、射向、末级滑行时间3个参数有可能显著影响发射轨道与出发条件的拼接结果以及具体实现的运载能力大小[8,10]。如果发射场位置确定,则这一问题转化为基于射向与滑行时间约束下的双曲线轨道发射运载能力计算。本文将基于“赤纬-发射能量”图方法,对考虑火箭射向和滑行时间约束的发射轨道运载能力计算进行研究,提出一种基于射向约束表达的无量纲运载能力折算方法,并通过算例进行说明和分析。
1 轨道模型与运载能力折算方法
1.1 双曲线轨道发射速度计算
目前,双曲线发射轨道初步计算主要基于引力影响球模型,即以双脉冲直接转移为例,首先确定出发时间历元1t和到达时间历元2t,通过星历计算得到出发时刻位置矢量1x和到达时刻位置矢量x2。本文中,统一使用开源的DE405模型。获得位置信息后,迭代兰伯特问题求解函数Lambert,根据首末状态位置矢量和转移时间,即可获得双曲线出发速度vdpt[11]:
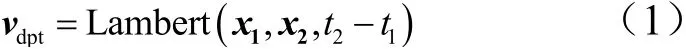
式中vdpt为出发速度矢量。
根据出发时刻地球在日心系下速度矢量Ev,可将双曲线出发速度vdpt转化为地心系表达,即为在地心系中的逃逸速度vesc:

vesc的平方也被称为发射能量(C3),其可用于描述运载火箭发射能力大小:

通过式(1)~(3)可知,对于不同出发和到达时间的双曲线轨道,其需要的出发速度是不同的,运载火箭要根据逃逸速度需求去匹配适当的发射参数,以满足轨道拼接要求。
1.2 发射轨道拼接可行域分析
已知需要的逃逸速度vesc后,需要进一步匹配满足工程约束的运载火箭发射轨道。一般来讲,运载火箭发射双曲线轨道需要通过近地停泊轨道进行过渡,以保证发射轨道和逃逸轨道拼接具有更大自由度。如图1所示,火箭末级和有效载荷组合体在近地停泊轨道上滑行至P点后进行逃逸加速,经由双曲线轨道飞出地球引力影响球。如要保证逃逸速度大小和方向相同,则所有可拼接的停泊轨道均必经过公共点M,即可绕vesc的地心矢量轴旋转。
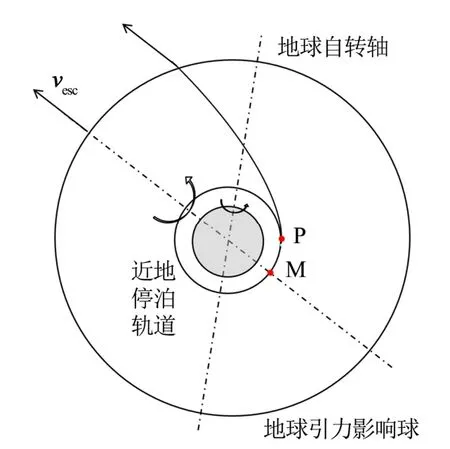
图1 双曲线发射轨道与停泊轨道拼接示意Fig.1 Hyperbolic Launch Orbit and Parking Orbit Splicing
在确定发射场地理位置和停泊轨道圆半径前提下,如果火箭末级和有效载荷组合体只采取1次切向脉冲加速逃逸,则双曲线出发轨道与运载火箭发射弹道拼接只具有1个自由度,这一自由度表示为停泊轨道圆绕逃逸速度地心矢量轴的转角。
发射场纬度、射向、末级滑行时间3个参数会在这一自由度上产生约束,且相互影响。令发射场纬度为B,极性定义北纬为正,南纬为负。令火箭发射射向为A。则利用式(4),可以计算射向约束下的双曲线发射停泊轨道公共点M的赤纬δ范围。

式中δ为赤纬;A为火箭发射射向;B为发射场纬度。
进一步假定运载火箭末级滑行时间约束对应停泊轨道上的地心角为φp,由发射点进入停泊轨道射程对应地心角为φL,经过停泊轨道公共点M后的逃逸段滑行地心角为φMP,则根据式(5),可计算在滑行时间约束下的停泊轨道公共点M的赤纬范围:
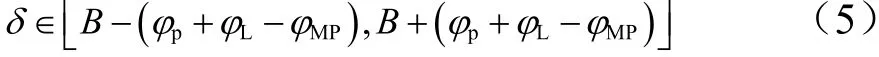
式中φp为滑行段地心角;φL为发射点进入停泊轨道段地心角;φMP为逃逸段地心角。
式(5)中,火箭由发射点进入停泊轨道入轨点的射程地心角φL在初步分析中可认为是定值,并由火箭射程计算,本文计算中取为0.31 rad。火箭滑行时间地心角φp可以根据滑行时间约束tp、停泊轨道半径Rp、地球引力常数μ计算:

式中tp为滑行时间约束;Rp为停泊轨道半径;μ为地球引力常数。
经过停泊轨道公共点后的逃逸段滑行地心角为φMP与停泊轨道半径Rp和逃逸速度vesc大小有关,如式(7)所示。
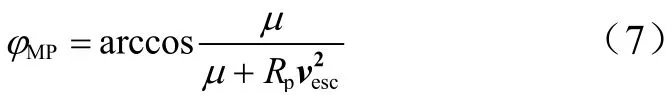
式(7)中,vesc可由式(2)计算得到。至此,根据双曲线出发速度,已能求解确定满足射向与滑行时间约束的发射可行域范围。在发射场纬度、停泊轨道半径、射向和滑行时间确定的情况下,这一约束表示为逃逸速度赤纬与发射能量集合的交集。
1.3 不同射向运载能力折算方法
在双曲线发射轨道满足发射约束基础上,可进一步计算火箭实现的运载能力大小。一般来讲,末级滑行时间对运载能力影响微小,初步分析中可认为不变。发射射向对运载能力影响较大,90°正东发射时,火箭能最大程度利用地球自转产生的初始速度,因此同一型火箭按相同程序飞行时,正东发射能够实现最大运载能力,随着射向逐步偏离正东,运载能力逐步减小,直到射向为正西270°时,运载能力最低。
初步分析中,可用式(8)估算某射向A下有可能达到的最大无量纲运载能力m,其中k为射向变化带来的运载能力损失系数,初步分析中可取为0.2,即正东发射实现最大无量纲运载能力,此时m为1,随着射向逐步由正东变化至正西,m减小至0.8。

在此基础上,针对特定射向范围的发射轨道,出于航落区限制,会调整加注量和俯仰飞行程序角等参数,以保证航落区安全。因此,特定射向下实现的上升段飞行轨迹未必是运载能力最优。此类约束只针对特定射向,所以可在式(8)基础上,减去特定射向范围内的方波函数以拟合实际轨道设计结果,如式(9)。

式中η为方波函数特征宽度;τ为运载能力折损幅度特征量。
式(9)中,Fi(A,Ai,η,τ)为射向Ai下的运载能力折损函数,其中η为方波函数宽度,即产生运载能力折损的射向区间大小,τ为运载能力折损幅度。Fi一般表达式为

假设射向Ai取97.5°附近时,出于航落区安全考虑,会产生运载能力损失,此约束下方波函数宽度取为15 °,即90~105 °射向范围都会受到损失,折损系数τ取1%,则在考虑这一特定射向折损情况下的运载能力函数示意见图2。
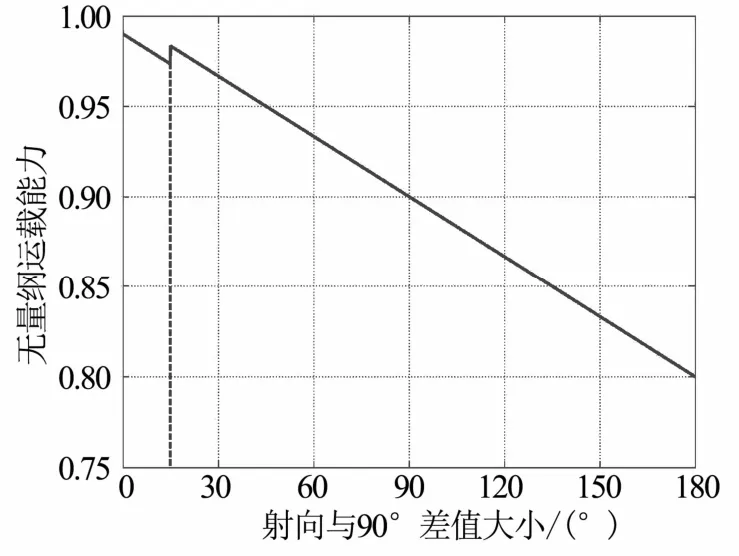
图2 考虑特定射向损失的运载能力折算函数Fig.2 Carrying Capacity Conversion Function Considering Loss of Specific Launch Azimuth
在考虑多射向约束的运载能力分析计算中,可设置多个Fi函数叠加,从而使得总的运载能力折算函数接近真实设计状态。根据本章以上内容,可用图3中的计算流程图表示深空发射运载能力计算过程。
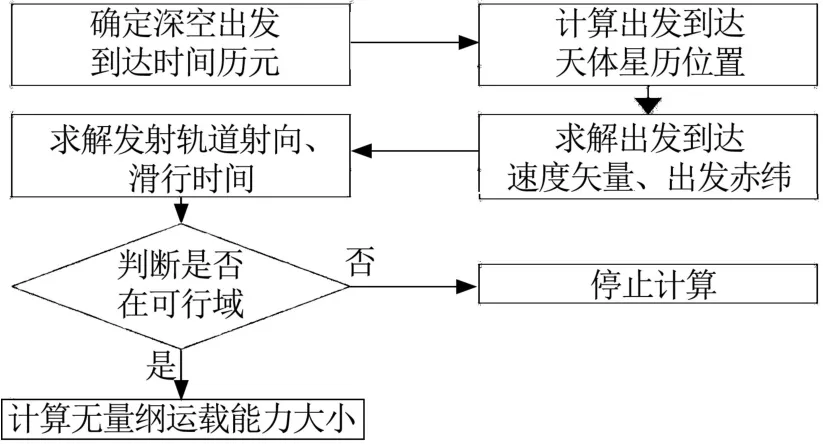
图3 深空发射运载能力计算流程Fig.3 Calculation Flowchart of Carrying Capacity in Deep Space Launch
2 满足发射约束的运载能力计算与分析
考虑某发射场位于北纬20°位置,发射射向约束为90~130°,运载火箭末级滑行时间约束为950 s内,通过式(4)~(7),能够得出满足发射约束的双曲线轨道“赤纬-发射能量”可行域(见图4)。
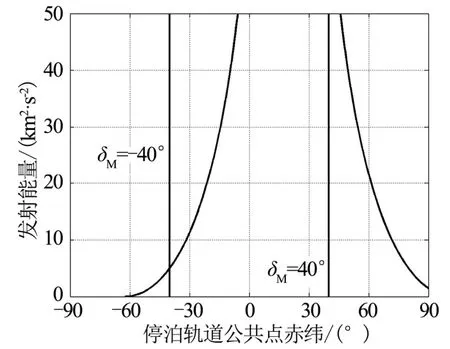
图4 “赤纬-发射能量”可行域范围Fig.4 Feasible Range of Declination-launch Energy
图4中,射向可行域为两条垂直线之间,关于0°对称分布,与发射能量无关。滑行时间约束为两条曲线之间,关于发射场纬度对称分布,在本文算例中,约束可行域随发射能量增加而变窄。两类可行域叠加后,即为同时满足射向约束和滑行时间约束的可行域集合,落在这一范围外的逃逸速度无法被满足。
在判断发射可行性之后,进一步引入运载能力折算函数。首先,针对图4可行域中的每一个点,其均对应多种射向与滑行时间组合的发射选择,对运载能力产生主要影响的参数是发射射向。因此,由式(4)计算图4中任意一点可能的发射射向范围,如式(11)。

将式(11)所得的射向范围代入式(9),即可以映射得到这一射向范围下所能够实现的运载能力范围,选取这一范围的最大值作为该点的最大运载能力,并将这一数值表示到“赤纬-发射能量”可行域中,如图5所示。
在图5中,所有发射可行域内的点均已优化得到最大运载能力发射方案,可见其沿射向等值线分布,在能够接近实现90°射向处,无量纲运载能力最大,随着可实现的射向远离90°,无量纲运载能力逐步降低,直至触碰可行域边界。
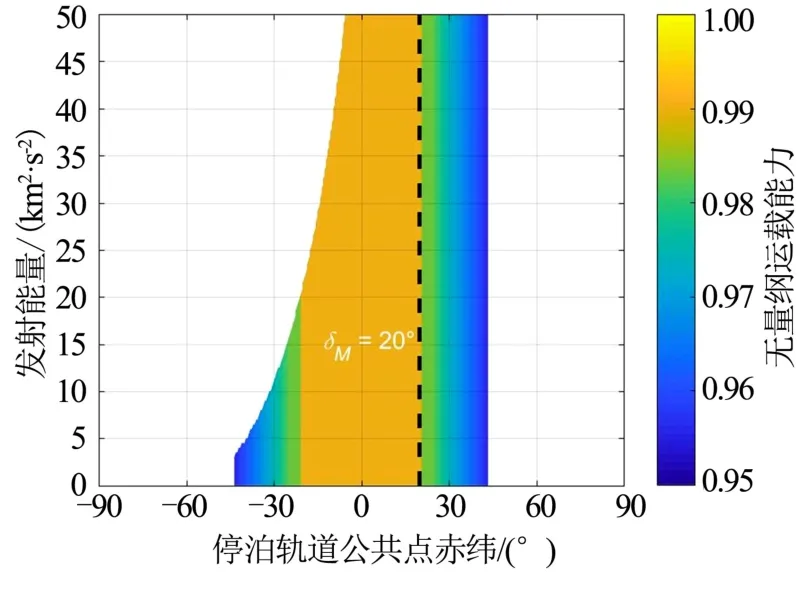
图5 逃逸速度可行域内运载能力Fig.5 Carrying Capacity in Feasible Region of Escape Velocity
以上计算过程与发射任务无关联,即说明可针对某一型运载火箭在特定发射约束下实现的双曲线轨道发射能力进行全面评估,并且找到射向和滑行时间约束边界,以供任务选择和后续改进设计参考。
3 假想算例分析
在实际的双曲线轨道任务规划中,初步阶段往往需要优化得到多个轨道方案,此后在论证过程中对比选择。在这一类具有明确任务背景的分析中,利用第2章提出的方法能够快速计算多个不同发射方案实现的运载能力大小,以供任务规划选择。本章将通过3个具体算例进行分析和说明。
3.1 算例1任务分析
根据假想任务探测轨道需求,首先根据式(1)~(2),计算得到出发速度增量Pork-Chop图(见图6)。
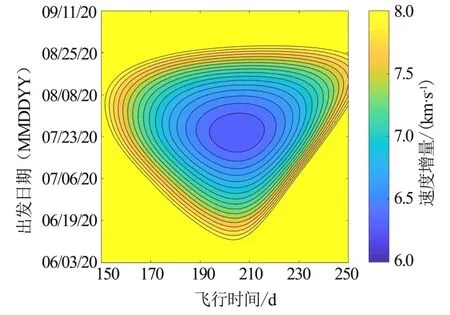
图6 算例1任务窗口总速度增量Fig.6 Total Velocity Increment of Eg.1 Launch Window
将图6中满足总速度增量小于8 km/s的点全部选出,并计算其需要的出发双曲线速度及其对应的出发速度赤纬与发射能量大小,运载能力在图中以散点形式画出,见图7。
从图7中可以看出,算例1窗口满足要求的出发点全部位于可行域内,同时均处在最大运载能力发射范围,表明这一窗口的出发条件均可被满足,且无运载能力损失,是一个适合执行发射的窗口。
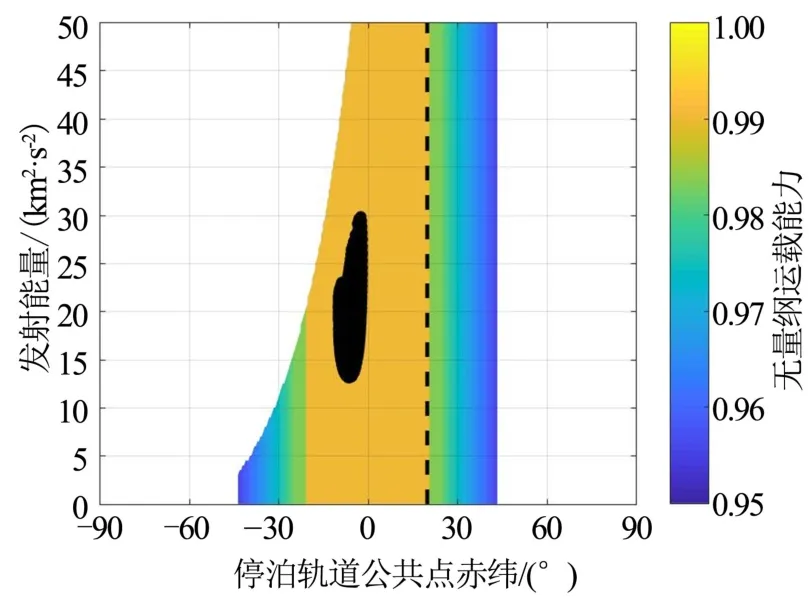
图7 算例1探测窗口运载能力计算Fig.7 Carrying Capacity Calculation of Eg.1 Launch Window
3.2 算例2任务分析
按3.1节中同样方法,基于算例2双曲线轨道需求,根据式(1)~(2),计算得到出发速度增量Pork-Chop图(见图8)。
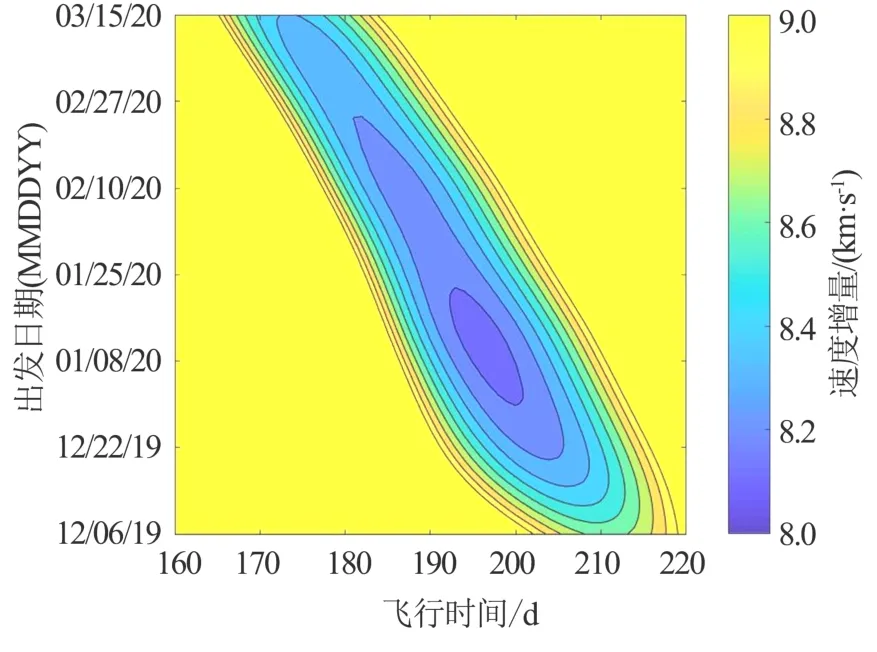
图8 算例2窗口总速度增量Fig.8 Total Velocity Increment of Eg.2 Launch Window
将图8中满足总速度增量小于9 km/s的点全部选出,并计算其对应的出发速度赤纬与发射能量大小,在运载能力图中以散点形式画出,见图9。

图9 算例2探测窗口运载能力计算Fig.9 Carrying Capacity Calculation of Eg.2 Launch Window
从图9中可以看出,算例2窗口满足要求的出发点也全部位于可行域内,且无运载能力损失,双曲线轨道出发条件均可被满足,是一个适合执行发射的窗口。
3.3 算例3任务分析
按3.1和3.2节中同样方法,根据算例3双曲线轨道需求计算出发窗口。首先根据式(1)~(2),计算得到出发速度增量Pork-Chop图(见图10)。

图10 算例3窗口总速度增量Fig.10 Total Velocity Increment of Eg.3 Launch Window
将图10中满足总速度增量小于14 km/s的点全部选出,并计算其对应的出发速度赤纬与发射能量大小,在运载能力图中以散点形式画出,见图11。
从图11中看出,总速度增量较低的散点部分落在了发射可行域范围之外,表明这些出发速度无法被满足。同时,也有部分出发点位于非最大运载能力范围,表明如果选择这一窗口,可能会承担部分运载能力损失,这一信息可供任务规划时参考使用。

图11 算例3探测窗口运载能力计算Fig.11 Carrying Capacity Calculation of Eg.3 Launch Window
4 结论与展望
本文研究了基于发射约束的双曲线轨道运载能力计算方法,得到以下结论:
a)提出了一种基于射向约束的运载能力折算函数,能够模拟射向变化和航落区调整带来的运载能力损失。利用这一函数可以在轨道初步设计与优化中快速模拟实际发射能够实现的运载能力大小。
b)利用双曲线轨道速度“赤纬-发射能量”图方法,展现了射向约束产生的无量纲运载能力变化规律,这一结果能为工程任务规划提供参考。分别以3个假想算例为例,分析了指定窗口的发射适应能力。
对后续研究进行展望,本文未考虑火箭末级滑行时间变化对运载能力造成的小幅影响,在后续研究中可以深入分析,以得到更贴合工程实际的设计结果。

