一类1∶2共振的Hamilton系统在分段n次多项式扰动下Abel积分的零点个数
曾 慧,李宝毅,张永康
(天津师范大学 数学科学学院,天津300387)
1 引言与主要结果
正规形理论是研究非线性微分方程奇点附近轨线结构的基本工具.在奇点处线性部分矩阵为非平凡幂零阵的平面微分系统的r阶正规形为[1]

其中:ai、bi∈R相关文献对系统(1)的分岔问题做了大量研究[2-7].文献[2-4]研究了当a2b2≠0时,系统(1)的余维2分岔.文献[5]和文献[6]分别研究了当a2b2=0时,系统(1)的余维3和余维4的分岔.文献[7]研究了当a2=b2=0,a3b3≠0时,系统(1)为1∶2共振的余维2的退化系统x˙=y,y˙=a3x3+b3x2y,给出了其普适开折

其中ε1、ε2为开折参数.当ε1>0时,通过适当的尺度变换可将系统(2)转化为

该系统可看作是Hamilton系统

的扰动系统.文献[8]利用广义Rolle定理证明了Hamilton函数是4次多项式)的平面Hamilton系统在n次多项式扰动下Abel积分的孤立零点个数不超过7n+5.文献[9]研究了具有“8字环”的Hamilton系统x˙=2y,y˙=λ+2x-4x3(λ∈在n次多项式扰动下Abel积分的孤立零点个数.文献[10]研究了四次椭圆Hamilton向量场在三次多项式扰动下极限环的个数.文献[11]利用Petrov的复域方法证明了在n次多项式扰动下,向量场(3)-在周期闭轨族Γh(h∈(0,+∞))附近分支出的极限环个数不超过n+1(实际上证明了不超过2[(n+1)/2]).
近年来,受到力学、电器工程和自动化控制中不连续现象的影响,相关学者对分段光滑的微分系统产生了浓厚的兴趣.对于分段光滑微分系统,一个重要的问题就是确定极限环的个数.文献[12-14]通过计算Lyapunov常数研究了分段开关系统极限环个数的上界.文献[15-16]利用平均法研究了不连续分段系统的周期解.文献[17-21]利用Melnikov函数法研究了分段近Hamilton系统周期解附近分支出极限环的个数.
本文利用Melnikov函数法并结合广义Rolle定理讨论当平面分为左右2个区域时,系统(3)-在分段n(≥2)次多项式扰动下Abel积分的孤立零点个数.考虑系统

其中:0<ε≪1,且

当ε=0时,系统(4)0的Hamilton函数为

当h∈(0,+∞)时,系统(4)0存在顺时针走向的周期闭轨族Γh=Γh+∪Γh-,其中:

设Γh与x轴正半轴交于与x轴负半轴交于与y轴正半轴交于,与y轴负半轴交于其中
本文的主要结果如下:
定理对于h>0,系统(4)ε的周期闭轨族Γh在分段n(≥2)次多项式扰动下,当Abel积分
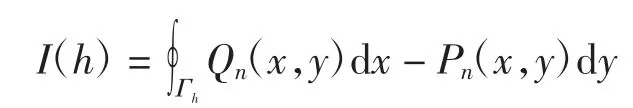
不恒为零时,I(h)的孤立零点个数不超过2n+7[n/2]+1.
2 Abel积分的计算
由Γh的对称性易得
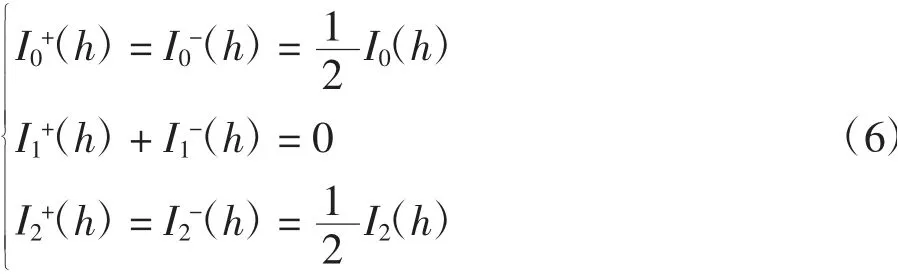
引理1若k为偶数,则有

若k为奇数,则有
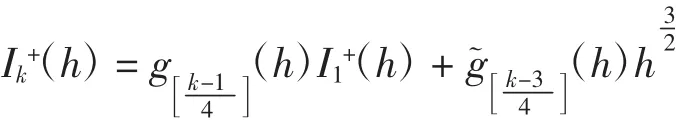
证明 利用数学归纳法证明.首先证明k为偶数的情形.由分部积分和式(5),当s≥4时,有

变形得

显然,当k=0、2时,引理1成立.假设当k≤2M-2(M≥2)时引理1成立,则当k=2M时,有
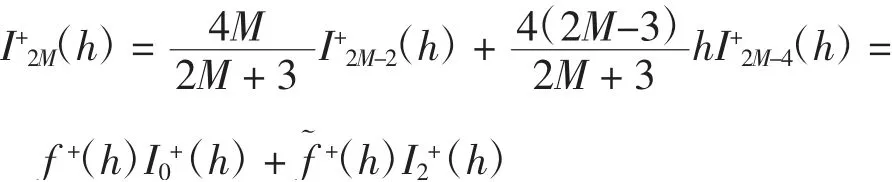
其中:
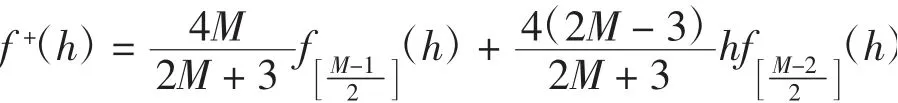

从而有

因此,当k=2M时,引理1成立.
下面证明k为奇数的情形.当k=1时,引理1显然成立.当k=3时,有


其中:

从而有

因此,当k=2M+1时,引理1成立.引理证毕.
命题系统(4)ε的Abel积分可以表示为

其中:
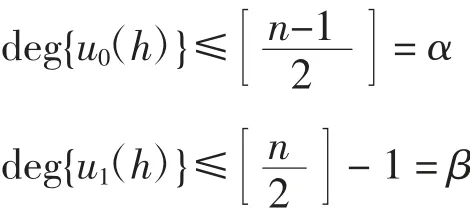
deg{u2(h)}≤α-1,deg{u3(h)}≤β+1
证明当x≥0时,注意到



同理可得,当x<0时,有


首先利用数学归纳法证明下面的式(10)成立.

其中系数多项式满足

当n=0时式(10)成立.
当n=1时,式(10)成立.
假设当n≤2k-1时式(10)成立,则当n=2k时,结合引理1,式(10)新增加的项为



因此,当n=2k时,有

其中系数多项式满足

即当n=2k时式(10)成立.
当n=2k+1时,结合引理1,式(10)新增加的项为


其中系数多项式满足

因此,当n=2k+1时,有

其中系数多项式满足

即当n=2k+1时式(10)成立.综上可得式(10)成立.
结合式(9),类似于式(10)的证明可得

其中系数多项式满足

结合式(6)和式(8)~式(11)可得

其中系数多项式满足

命题证毕.
引理2满足Picard-Fuchs方程组
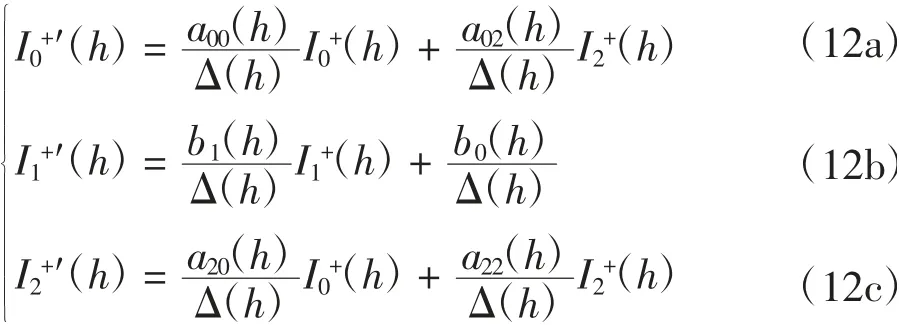
证明由文献[11]的引理3可知式(12a)和式(12c)成立.下证式(12b)成立.

对式(13)关于h求导,可得

另一方面,利用分部积分可得

变形得

结合式(7)可得
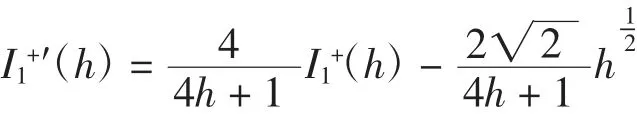
引理证毕.
推论1满足Picard-Fuchs方程组

对式(14a)和式(14c)求导,可得推论2.
推论2满足微分方程组

3 Abel积分孤立零点个数的估计
引理3[22]设A(h)和B(h)在开区间(a,b)上分别有个和个零点(计重数若方程A(h)·满足:
(1)P(h)在闭区间[a,b]上连续,在开区间(a,b)上可导;
(2)A(h)与B(h)在闭区间[a,b]上连续,F(h,P)在[a,b]×[mP,MP]上连续,其中[mP,MP]是P(h)在[a,b]上的值域.
则函数P(h)在开区间(a,b)上至多有个零点(计重数).
引理4设且deg{v2(h)}≤deg{v0(h)}≤deg{v2(h)}+1,则

其中:k≥2,deg{v0,k(h)}≤deg{v0(h)}+k-1,deg{v2,k(h)}≤deg{v2(h)}+k-1.
证明利用数学归纳法证明.当k=2时,对F(h)求二阶导数,结合推论1和推论2可得

其中:

从而有

则当k=2时,引理4成立.假设当k=η≥2时引理4成立,则当k=η+1时,结合推论1有

其中:
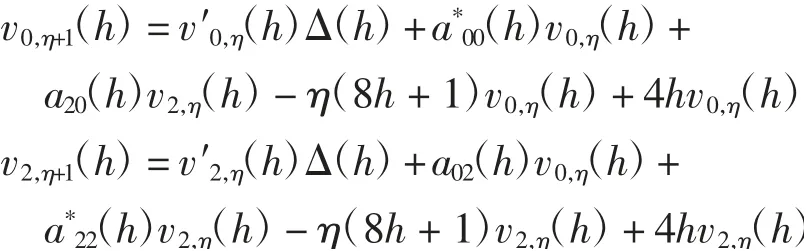
从而有

即当k=h+1时引理4成立.引理证毕.
定理的证明当n≥2时,由命题可知

对I*(h)关于h求导,并结合推论1可得

其中:


其中:

且deg{v0(h)}≤α+β+1,deg{v2(h)}≤α+β,deg{v3(h)}≤2β+2.
在引理4中,令k=(2β+2)+1=2β+3,可得


由文献[11]的定理1可得

则有
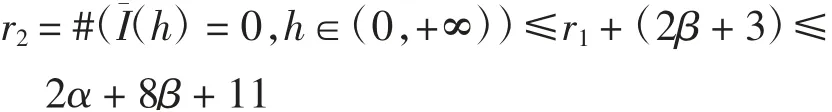
结合式(15)和式(17)及引理3可得

定理证毕.
——对2018年广州市一道中考题的研究

