具有有限个子代数的李代数

王健戍，胡志广

（天津师范大学数学科学学院，天津300387）

在李代数研究领域中，分类问题是一个基本问题.著名的Levi定理说明任意复李代数可分解为可解理想与半单子代数的线性空间直和.因此，研究复李代数的分类可归结为分别探究可解李代数和半单李代数的分类.半单李代数的分类已完全解决[1-2]，而可解李代数的分类极其复杂，是李代数中未完全解决的一个基本问题.文献[3]给出了4维可解李代数的分类，文献[4]给出了6维可解李代数的分类情况.另外，相关学者考虑一些满足特殊条件的李代数，对其结构和分类进行了研究[5-16].文献[5]给出了具有有限多个理想的李代数分类；文献[9]给出了子空间均为子代数的李代数的结构；文献[11]研究了一类实可解李代数的分类；文献[12]研究了几类低维幂零李代数的结构；文献[13]对导代数维数小于4时的非交换n-李代数进行了分类；文献[16]研究了8维幂零李代数的分类.本文考虑具有有限多个维数大于1的子代数的李代数，证明了此类李代数的维数小于3.

1 预备知识

本文约定所讨论的李代数都是复数域上的.

定义1设L为李代数，L中的理想序列L(0)=L，…，L(i)=[L(i-1)，L(i-1)]，…称为L的导代数序列.若存在自然数N，使得L(N)=0，则称L为可解李代数.

引理1[4]设L为3维复可解李代数，X、Y、Z是L的一组基，则在同构意义下L可分为以下5类：

在引理1中，L1为交换李代数，L2为幂零李代数，L3为1维子代数和非交换2维子代数的直和，L4θ和L5为非可分可解李代数.

定义2设L为李代数，L中的理想序列

称为L的降中心序列.若存在自然数N，使得LN=0，则称L为幂零李代数.

引理2[17]设L为幂零李代数，则ei，i=1，2，…，s是L的生成元的充分必要条件是ei+L1，i=1，2，…，s为L/L1的一组基.

2 主要结果

命题1特殊线性李代数sl（2，C）={A∈gl（2，C）|trA=0}有无穷多个2维子代数，其中gl（2，C）为域C上2阶矩阵的全体，其括积为

证明取sl（2，C）中的一组标准基

则其李括号运算为[h，x]=2x，[h，y]=-2y，[x，y]=h.

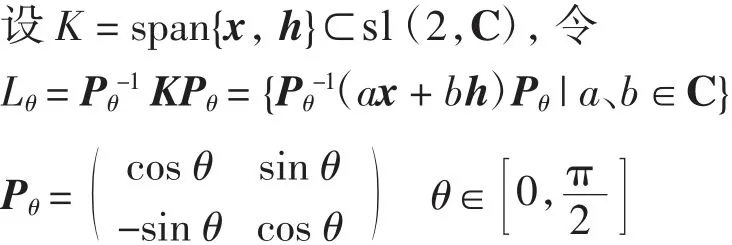
显然Lθ是sl（2，C）的2维子代数.

注意到，Lθ中的幂零元为其中a∈C，因此，若则存在k∈C，满足，即

由方程组

可得k=1，且tan2θ1=tan2θ2，θ1=θ2.因此Lθ，θ∈为sl（2，C）的互不相同的子代数.命题证毕.

命题2设L为可解李代数，且L具有有限多个维数大于1的子代数，则L是维数小于3的交换李代数，或者L=L1+Cα（直和），其中α∉L1.

证明当L=0时，命题显然成立.

当L≠0时，因为L为可解李代数，故L真包含L1.于是dimL/L1>0.

若dimL/L1≥3，因为L/L1可交换，则L/L1有无穷多个2维的子代数Kθ，θ∈Λ（指标集）.令π：L→L/L1为自然同态，于是π-1（Kθ），θ∈Λ为L的维数不小于2的子代数，此时不满足条件.

若dimL/L1=2，则L/L1的非平凡子代数都是1维的，且有无穷多个.考虑这些1维子代数在L中的原像.若dimL1≠0，则由维数公式可知，这些原像均为维数大于1的子代数，与条件矛盾，从而dimL1=0，因而L是2维交换李代数.

若dimL/L1=1，则存在α∈L-L1，满足L=L1+Cα.当L1=0时，L为1维李代数；当L1≠0时，L的形式为L1+Cα，其中α∉L1.

综上可知，L是维数小于3的交换李代数或者L=L1+Cα，α∉L1.命题证毕.

推论设L为幂零李代数，且L具有有限多个维数大于1的子代数，则L是维数小于3的交换李代数.

证明因为L为幂零李代数，所以L可解.若L1=0，则由命题2可知结论成立.若L1≠0，则L=L1+Cα（直和），其中α∉L1，于是α+L1为L/L1的基，由引理2可知，α为L的生成元，故dimL=1，与L1≠0矛盾.证毕.

定理设L为复李代数，则L只有有限多个维数大于1的子代数，当且仅当L是维数小于3的李代数.

证明充分性显然成立.下证必要性.

根据Levi定理，L中存在半单子代数C，使得L=C+R为空间直和，其中R为L的根基.

假设C≠0，则C中一定存在同构于sl（2，C）的3维子代数，由命题1可得，sl（2，C）有无穷多个2维子代数，所以L中也有无穷多个2维子代数，与条件矛盾.因此C=0，所以L为可解李代数.

由命题2可得，L是维数小于3的交换李代数，或者L=L1+Cα（直和），α∉L1.

假设dimL≥3，此时L的形式是L=L1+Cα（直和），其中α∉L1，注意到L1是幂零李代数，且只有有限多个维数大于1的子代数，则根据推论1可知，L1为2维交换李代数.因而dimL=3，此时L为3维可解李代数，且其导代数是2维交换子代数.由引理1中3维复可解李代数的分类，易知L1、L2和L3均不满足条件.对于任意的k1∈C，注意到K1=span{X，k1Y+Z}⊂L4θ为L4θ的2维子代数，故L4θ不满足条件.对于任意的k2∈C，由K2=span{X，k2Y-Z}⊂L5为L5的2维子代数，可知L5也不满足条件.综上可知3维可解李代数中不存在满足条件的李代数，因此L是维数小于3的李代数.定理证毕.