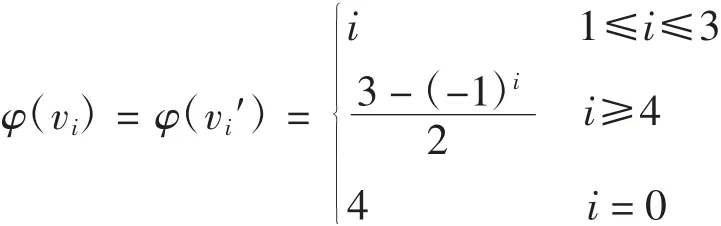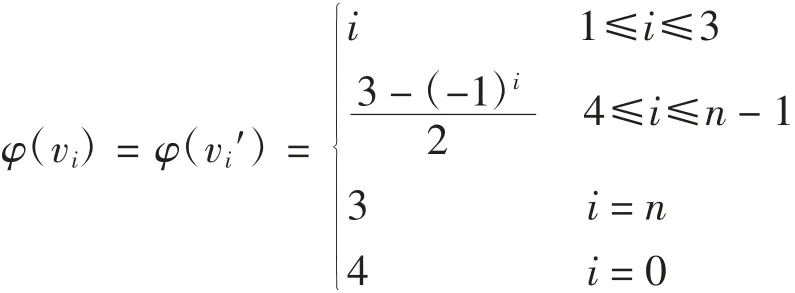特殊点分裂图的Grundy着色问题
杨晨旭,姚庆烨,邓兴超
(天津师范大学数学科学学院,天津300387)
1 引言和预备知识
近些年,图的着色理论随着计算机理论的发展得到进一步完善,基于实际和理论需要,各种类型的着色问题被提出[1-3].Grundy着色最早由Christen等[4]基于贪婪算法提出,并讨论了完美图的Grundy着色.文献[5]讨论了Grundy着色算法的复杂性问题.文献[6]讨论了Grundy着色的Nordhaus-Gaddum-type不等式.有关Grundy着色的最新进展可参见文献[7-8].本文考虑路、圈、轮和扇的点分裂图的Grundy着色问题,通过构造出具体的着色方案,利用反证法得到这4类特殊点分裂图的Grundy色数.
本文研究的图是有限、无向的简单图(无重边且无自环).顶点集合为V、边集合为E的图记为G=(V,E).υ(G)表示图G的阶,即υ(G)=|V(G)|.在不引起歧义的情况下,图G的边数用e(G)表示,即e(G)=|E(G)|.对于v∈V(G),用NG(v)表示顶点v的邻域,v的度记为d(v),即d(v)=|NG(v)|,图G的最小度和最大度分别记为δ(G)和Δ(G).对于S⊆V(G),由顶点集S导出的子图记为G[S],并将G[VS]记为GS或G-S,特别地,记G[V{v}]=G-v,G的补图记为G.对于2个正整数m 定义1[9]图G(V,E)的k正常着色是指一个映射φ:V→[1,k],满足:对于任意边uv∈E(G),φ(u)≠φ(v).若图G存在一个正常的k着色,则称图G是k可着色的,称χ(G)=min{k|图G存在一个正常的k着色}为图G的色数. 定义2[6](Grundy着色)设k>0且k∈N,图G(V,E)的Grundy着色是指一个映射φ:V→[1,k],满足以下条件: (1)对于任意边uv∈E(G),φ(u)≠φ(v). (2)对于满足1≤m 引理1[10]对于任意图G,有χ(G)≤Γ(G). 引理2[10]对于任意图G,有Γ(G)≤Δ(G)+1. 定义3[9]设G和H为2个点不交的图,G和H的联图G∨H定义为 定义4[11]设G为简单图,其顶点集为V(G)={v1,v2,…,vn},设I2为含有2个点的独立集.用I2替换G的每个顶点得到的图记为G[I2].I2中的每个点仍按对应点的连边方式与其他点相连.G[I2]的点集和边集分别为 称G[I2]为G的点分裂图. 例如:一条边K2的点分裂图为K2[I2]≃C4. 定理1路Pn的点分裂图Pn[I2]的Grundy色数Γ(Pn[I2])为 证明(1)当n=2时,P2[I2]≃C4,设φ(v1)=1,φ(v3)=1,φ(v2)=2,φ(v4)=2,则φ为P2[I2]的一个Grundy 2着色函数.由引理2可知Γ(P2[I2])≠3,所以Γ(P2[I2])=2. (2)当n=3时,设φ(v1)=1,φ(v2)=2,φ(v3)=1,φ(v1′)=1,φ(v2′)=2,φ(v3′)=1,则φ为P3[I2]的一个Grundy 2着色函数.下面证明Γ(P3[I2])<3,由Grundy着色的定义可知,顶点v1至多可着3种颜色,不妨设φ(v1)∈{1,2,3}. 情况1当φ(v1)=1时,由引理2可知,φ(v2)∈{2,3,4,5},φ(v2′)∈{2,3,4,5}.如果φ(v3)=3,则有φ(NG(v3))={φ(v2),φ(v2′)}={1,2},但v1∈{NG(v2)}且φ(v1)=1,与定义矛盾.因此φ(v3)=2或φ(v3′)=2,则由定义可得1∈φ(NG(v3)),即φ(v2′)=1或φ(v2)=2.若1∈φ(NG(v3′)),即φ(v2′)=1或φ(v2)=1,但v1与v2和v2′相邻,矛盾. 情况2当φ(v1)=2时,有φ(NG(v1))={1},因为NG(v1)=NG(v3)=NG(v3′)={v2,v2′},则φ(v2)=1,φ(v2′)=1,从而Γ(P3[I2])<3. 情况3当φ(v1)=3时,有φ(NG(v1))={1,2},NG(v1)=NG(v3)=NG(v3′)={v2,v2′},因此φ(v2)=1,φ(v2′)=2或φ(v2)=2,φ(v2′)=1,若φ(v2)=1,φ(v2′)=2,则要保证φ(NG(v2′))={1},因为NG(v2′)={v1,v3,v3′},但是NG(v2′)=NG(v2),所以这是不可能的.若φ(v2)=2,φ(v2′)=1,则要保证φ(NG(v2))={1},但是NG(v2′)=NG(v2)={v1,v3,v1′,v3′},显然v1不能着颜色1,因此Γ(P3[I2])<3. 综上可得Γ(P3[I2])=2. 由着色函数可知φ(v1)=1,φ(v1′)=1;当i>3且为偶数时,φ(vi)=1,φ(v2)=2,φ(v2′)=2;当i>3且为奇数时,φ(vi)=2.故当i>3且为奇数时,上述着色函数满足1∈φ(NG(v2))且1∈φ(NG(vi)),又因为φ(v3)=3,φ(v3′)=3,NG(v3′)={v2,v2′,v4,v4′},φ(v4)=1,φ(v4′)=1,φ(v2)=2,φ(v2′)=2,因此有{1,2}⊆φ(NG(v3)),{1,2}⊆φ(NG(v3′)),所 以φ是 一 个 真Grundy 3着色.当i>3且为偶数时,同理可得φ是一个真Grundy 3着色. 由引理2可知Γ(Pn[I2])∈{3,4,5},要证明Γ(Pn[I2])=3,只需证明Γ(Pn[I2])∉{4,5}. 首先证明Γ(Pn[I2])≠5.若Γ(Pn[I2])=5,则存在某个顶点v,满足φ(v)=5且v是度最大的顶点,即d(v)=4,否则其邻点集着色不满足定义要求. 用{v-2,v-1,v,v1,v2}和{v-2′,v-1′,v′,v1′,v2′}表示v的邻点集合,其中v-2为v左边的第2个顶点.如果顶点v∈V(G),φ(v)=5,则要保证φ(NG(v))={1,2,3,4},因为d(v)=4,故有φ(v-1′)≠φ(v1′)≠φ(v1)≠φ(v-1). 假设φ(v-1)=3,由于d(v-1)=4,NG(v-1)={v-2,v,v-2′,v′},φ(v)=5,则要保证φ(NG(v-1))={1,2,3},又d(v-1)=4,所以φ(v-2′)≠φ(v2′)≠φ(v)≠φ(v′).不妨设φ(v′)=j,1≤j≤3,因为NG(v)=NG(v′),若v′着颜色j,而Grundy着色是正常着色,因此v′的邻点不能着颜色j,也就是v的邻点缺少颜色j,显然这种着色方法不满足定义,因此Γ(Pn[I2])≠5. 然后证明Γ(Pn[I2])≠4.若Γ(Pn[I2])=4,则存在顶点v,满足φ(v)=4,则要保证φ(NG(v))={1,2,3},因为d(v)=4,不妨设φ(v-1)=3,NG(v-1)={v-2,v,v-2′,v′},故有{1,2}⊆{φ(v-2′),φ(v2′),φ(v′)},显然这种着色方法不满足定义.当φ(v′)=4时,有{1,2}={φ(v-2′),φ(v2′)}.由于φ(NG(v-2))=φ(NG(v-2′)),若φ(v-2′)=1,则1∉φ(NG(v-2)),若φ(v-2′)=2,则1∉φ(NG(v-2′)),也不满足定义.因此Γ(Pn[I2])≠4. 经济的发展和生态环境的恶化使人们对森林资源的重视程度不断的提升,许多地区都在进行林业工程的建设,这使我国的森林资源走势发生变化,同时森林资源不断增加。然而在一些地区的林业工程建设中存在一定的问题,即营造林的质量不高。出现这种情况的因素有多种,尤其重要的是营造林质量不高。 综上可得Γ(Pn[I2])=3. 定理2圈Cn的点分裂图Cn[I2]的Grundy色数Γ(Cn[I2])为 证明(1)当n=4时,在圈上交替着颜色1和2即可,故Γ(C4[I2])=2. (2)当n≠4时,首先给出Cn[I2]的一个Grundy 3着色函数.当n为奇数时, 当n为偶数时, 利用与定理1类似的方法可证明φ是一个真Grundy 由引理2可知Γ(Cn[I2])∈{3,4,5},与路的点分裂图类似,可证明Γ(Cn[I2])≠4且Γ(Cn[I2])≠5,故Γ(Cn[I2])=3. 定理3扇Fn的点分裂图Fn[I2]的Grundy色数Γ(Fn[I2])为 证明(1)当n=2时,F2=C3,由定理2可得Γ(C3[I2])=Γ(F2[I2])=3. (2)当n=3时,在轮上交替着颜色1和2,轮心着颜色3即可,故Γ(F3[I2])=3. (3)当n≥4时,首先给出Fn[I2]的一个真Grundy 4着色函数 下面证明Γ(Fn[I2])<5.在Fn[I2]上,每个轮圈上顶点的度均为6,因此Γ(Fn[I2])≤7,否则与Grundy着色定义矛盾. 首先证明Γ(Fn[I2])<7. 情况1设在轮圈上存在一个顶点v,φ(v)=7,此时v-1′、v1′、v0′、v0、v-1、v1着颜色1,2,…,6,且各不相同,不妨设φ(v-1)=6,由于NG(v)=NG(v′),所以v′不能着颜色1、2、3、4、5,否则φ(NG(v))≠{1,2,3,4,5,6}.因此φ(v′)=7.又因为φ(v-1)=6,则φ(NG(v-1))={1,2,3,4,5},即v-2、v-2、v0′、v0′要用完1、2、3、4、5这5种颜色,这显然不可能.故φ(v-1)≠6,矛盾. 情况2若φ(v0)=φ(v0′)=7,则只需证明在轮圈上不存在顶点v,满足φ(v)=6.若顶点v在轮圈上,且φ(v)=6,顶点v和v0、v0′都相邻,因此v-2、v-1、v0′、v0′需着颜色1、2、3、4、5,且各不相同,这显然是矛盾的. 下面证明Γ(Fn[I2])<6. 情况1设在轮圈上存在一个顶点v,φ(v)=6,显然φ(v0)=φ(v0′),若φ(v0′)=φ(v0)=5,则有φ(v-1)≠φ(v1)≠φ(v-1′)≠φ(v1′)∈{1,2,3,4},不妨设φ(v-1)=4,则φ(v′)、φ(v-2′)、φ(v-2)中必有一个等于3.若φ(v′)=3,由NG(v)=NG(v′)可知3∉φ(NG(v)),矛盾;若φ(v-2′)=3,则有{φ(v-3),φ(v-3′)}={1,3},矛盾;同理,若φ(v-2)=3,也会导致矛盾. 情况2若φ(v0)=φ(v0′)=6,则只需证明在轮圈上不存在顶点v,满足φ(v)=5.若顶点v在轮圈上,且φ(v)=5,顶点v和v0、v0′都相邻,此时v-1′、v1′、v-1、v1着颜色1、2、3、4,并且各不相同,类似于情况1的证明过程可知这是矛盾的. 类似于Γ(Fn[I2])<7和Γ(Fn[I2])<6的证明,可以得到Γ(Fn[I2])<5.综上可得Γ(Fn[I2])=4. 定理4轮Wn的点分裂图Wn[I2]的Grundy色数Γ(Wn[I2])为 证明(1)当n=4时,令 容易证明φ是一个真Grundy3着色.又因为Γ(W4[I2])≤3,故Γ(W4[I2])=3. (2)当n≠4时,首先给出Wn[I2]的一个真Grundy 4着色函数.当n为奇数时, 当n为偶数时, 由Γ(Wn[I2])≤5,只需证明Γ(Wn[I2])≠5.设轮的中心为v0、v0′,并设{…,u-2,u-1,u1,u2,…}为某个轮的顶点集合.若Γ(Wn[I2])=5,则着颜色5的顶点位于轮上或中心,利用与定理3类似的证明过程可知这2种情况都是不可能的,因此Γ(Wn[I2])=4.
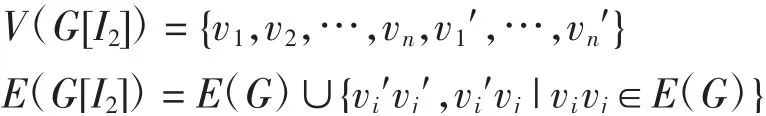
2 主要结果
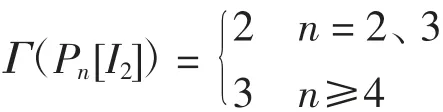


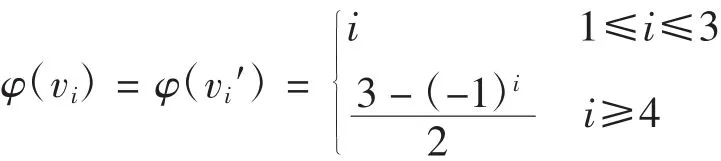

3 着色.