关于H1非协调虚拟元的若干估计
黄建国,余 跃
(上海交通大学数学科学学院,上海 200240)
虚拟元方法(VEM)由Beirao等在文[1]中提出,它是标准有限元在多角形或多面体网格上的推广. 其它开创性工作参见文[2-3]. 作为一个新的数值算法,近年来VEM得到快速发展,已广泛用于各种微分方程的数值求解[2-7]. 相比有限元,VEM能更方便地处理复杂区域上或具高正则性容许空间的变分问题的数值求解. 椭圆型方程非协调虚拟元的构造自然且标准,它可由微分算子的分部积分公式直接获得. 而且当多角形或多面体退化为单纯形时,VEM常给出标准有限元.
VEM理论分析的文章并不多,大多在网格满足星形条件下讨论,如文[5]中的假设A3. 陈龙和黄建国在文[8]中给出了一个更一般的假设,并在该假设下建立了H1协调虚拟元的若干误差估计,包括逆不等式、范数等价性和插值误差估计. 其假设如下:
A1. 在每个网格单元K∈Th上,存在一致正则和拟一致的“虚拟三角剖分”TK,并且TK的剖分尺寸与hK相当.此外,K的每一条边均是TK中某一三角形的边.
本文在假设A1下考虑二维H1非协调元的若干估计. 对逆不等式,本文把文[9]中处理协调元的技巧推广至非协调情形,给出一个重要函数分解,将其证明归结为调和情形. 该技巧适用于二阶和四阶椭圆问题的协调和非协调虚拟元. 在虚拟三角剖分上使用泡函数技巧,证明了迹不等式(4)或(5),从而获得逆不等式,详见定理1. 范数等价性推导的关键在于证明L2情形即(6)的上界估计. 本文分两步证明该上界估计,即建立自由度型的逆不等式(8)和自由度型的Poincare-Friedrichs不等式(9). 需要指出的是,文[7]给出了任意阶任意维非协调元的范数等价性和插值误差分析. 除了虚拟三角剖分假设外,该文还需另一假设. 对高维一般情形,该分析涉及诸多精细技巧. 本文则借助虚拟三角剖分,使用非常简单、直接的方法给出逆不等式和范数等价性结果. 在范数等价性的基础上,使用(10)这一简单关系式建立插值算子的L2稳定性,然后使用Bramble-Hilbert论证给出了插值算子的误差估计.
1 准备知识

H1非协调虚拟元方法由文献[4]提出,对k≥1,局部虚拟元空间定义为
Vk(K):={v∈H1(K):Δv∈Pk-2(K),v|∂K∈Bk(∂K)},k≥1,
式中,
Bk(∂K)={v∈C0(∂K):v|e∈Pk(e),e⊂∂K},
而C0(∂K)表示沿着单元K的边界∂K连续的函数集合.为了给出自由度,引入尺度单项式集合

·χ∂K(v):边上直到k-1阶的矩量,
χe(v)=|e|-1(me,v)e,me∈Mk-1(e),e⊂∂K.
·χK(v):单元K上直到k-2阶的矩量,
χK(v)=|K|-1(mK,v)K,mK∈Mk-2(K).
另外,以χ(v)记以上所有自由度形成的列向量.
经分部积分可知,椭圆投影可由前面所提自由度唯一确定.
为得后文诸估计,先给出几个常用不等式,见文[10].应强调指出,各不等式的隐藏系数仅依赖假设A1中的几何参数.
引理1成立如下不等式:
(1)Dupont-Scott定理:对任意的v∈Hl(K),存在多项式q∈Pl-1(K)使得
(2)Poincare-Friedrichs不等式:
(3)乘法型迹不等式:
(4)带几何尺度迹不等式:
2 逆不等式
逆不等式是有限元方法数值分析的重要工具.在文[9]中,对协调元情形,我们提出一个新的函数分解,将逆不等式的证明归结为调和情形.下面将其推广至非协调元情形.
引理2对任意满足Δv∈Pk-2(K)的v∈H1(K),存在多项式p∈Pk(K),使得Δp=Δv且
(1)
‖p‖0,K‖v‖0,K.
(2)
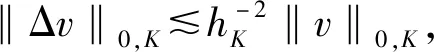
另一方面,由Poincare-Friedrichs不等式和已证的第二个不等式,有
‖p1‖0,KhK|v|1,K‖v‖0,K,
此p1即为所求.证毕.
定理1成立逆不等式
(3)

换言之,在逆不等式(3)中,不妨设在K上Δv=0,即讨论w=v-p时逆不等式(3)是否成立即可.
由分部积分公式及Cauchy-Schwarz不等式,得
根据乘法型迹不等式,
从而只要证明
(4)

因∂nw|e是多项式,将其沿着e的法向量方向常延拓到T上.记延拓后的函数为ET(∂nw|e),并令φ=beET(∂nw|e).注意到Δw=0,由分部积分和多项式的逆估计得
利用多项式的逆估计,并注意到常延拓,有
由此即得(4).证毕.
事实上,不等式(4)对非调和的v∈Vk(K)也成立.
推论1成立估计
(5)

最后一步用到引理2的第一式.结果得证.
3 范数等价性和插值误差估计
利用逆不等式可证明如下的范数等价性.
定理2对v∈Vk(K),成立
(6)
(7)
证明分为四步.
步1:建立l2-L2估计
对边界矩量,由Cauchy-Schwarz不等式得
使用迹不等式和前面已建立的逆不等式,有
于是
对内部矩量,直接估计有
步2:建立自由度型的逆不等式
|v|1,K‖χ(v)‖l2,v∈Vk(K).
(8)
分部积分有
对第一项,令g=-Δv=∑αgαmα,并记g=(gα).根据Cauchy-Schwarz不等式和文[8]中Lemma 4.1关于函数g的范数等价性结果,可知
使用引理2的第一个不等式,立得
从而
|-(v,Δv)K|=|(g,v)K||v|1,K‖χ(v)‖l2.
对第二项,令
类似有
使用推论1的不等式得
于是
联立以上诸式即得(8).
步3:建立自由度型的Poincare-Friedrichs不等式
(9)
结合步2的结果得第一式的上界估计.上式直接由Poincare-Friedrichs不等式和自由度的定义获得.

现在考虑插值误差估计.设IK:H1(K)→Vk(K)为节点插值算子,满足
χ(IKv)=χ(v),χ∈Xk(K),
式中,Xk(K)表示自由度集合.
定理3设v∈Hk+1(K),k≥0,则成立如下的最优误差估计
证明根据定理2的范数等价性以及插值算子的定义,有
‖IKv‖0,K≃hK‖χ(IKv)‖l2=hK‖χ(v)‖l2.
(10)
回顾定理2步1的计算可知,插值算子有如下的L2稳定性
‖IKv‖0,K‖v‖0,K+hK|v|1,K.
根据Dupont-Scott理论,存在多项式p∈Pk(K)使得
由三角不等式
‖v-IKv‖0,K≤‖v-p‖0,K+‖IK(v-p)‖0,K
以及已证的稳定性可知
类似地,由
|v-IKv|1,K≤|v-p|1,K+|IK(v-p)|1,K
并利用逆不等式
立得H1半模下的误差估计.证毕.

