有限域上的置换多项式

冯亚芳,周广良

(南京师范大学数学科学学院,江苏 南京 210046)

1863年,Hermite首次研究了Z/pZ上的置换多项式,并且给出了一些判别置换多项式的方法. 其后Dickson将置换多项式的概念推广到了任意的有限域中,并作了相关的研究. 在他的 《History of the Theory of Numbers》 一书中,整理了1922年之前的有关置换多项式的一些结果. 20世纪中期,Carlitz 等人做了一些新的研究,他们将Z/pZ上单变元的置换多项式推广到了剩余类环以及一般环上的多变元的置换多项式. 近100年的时间里,置换多项式的一些结论已经被广泛地应用于序列、密码理论与密码设计等领域,见文献[1-4].

定义1记K=Fq,E=Fqn为有限域,对于任意的x∈E,我们定义x在K上的迹函数为TrE/K(x)=x+xq+xq2+…+xqn-1.当q为素数时,我们把迹函数称为绝对迹函数,用Tr(x)来表示.

记K=Fq,E=Fqn迹函数有以下的几条性质:

(1) 对于任意的α,β∈E,TrE/K(α+β)=Tr(α)+Tr(β).

(2) 对于任意的α∈E以及c∈K,TrE/K(cα)=cTr(α).

(3) 对于任意的α∈K,TrE/K(α)=nα.

(4) 对于任意的α∈E,TrE/K(αq)=Tr(α).

引理1[5]对于任意的b,c∈F2m,F2m上的二次多项式x2+bx+c=0 在F2m内有解当且仅当Tr(b/a2)=0.

引理2设α,e均为正整数,d=(α,e),那么当e/d为奇数时(2α+1,2e-1)=1,当e/d为偶数时(2α+1,2e-1)=2d+1.

以下为主要结果的证明.

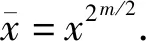
定理1设δ∈F2m,其中m是一个正偶数,0≠a∈F2m/2且Tr(δ/a2)=1,那么

f(x)=(x2+ax+δ)2m/2-1+x2m/2+1

是F2m上的一个置换多项式.

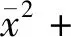
(1)

对(1)两侧提升2m/2次幂,得到:

(2)

(3)

另一方面,由(2)可以得到

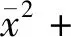
(4)

(3)与(4)两侧相减可得

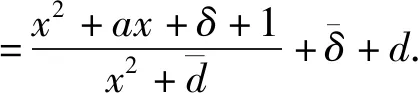
(5)

比较(3)(5)我们有

因此

简化可得

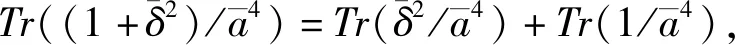
定理2设δ∈F2m且Tr(δ)=1,其中m≡0(mod 4),那么满足(2m/2-2)k≡2m/2-1(mod 2m-1)的正整数k,f(x)=(x2+x+δ)k+x是F2m上的一个置换多项式.

证明首先,同余方程(2m/2-2)k≡2m/2-1(mod 2m-1)有解当且仅当(2m/2-2,2m-1)|2m/2-1.因为m≡0(mod 4),所以2m-1为奇数.因此(2m/2-2,2m-1)=(2m/2-1-1,2m-1)=2(m/2-1,m)-1.上述条件转化成:2(m/2-1,m)-1|2m/2-1.也即(m/2-1,m)|m/2.由m≡0(mod 4)得m/2-1为奇数,则(m/2-1,2)=1且(m/2-1,m/2)=1.于是(m/2-1,m)=1|m/2.即上述同余方程有解.要证明f(x)是置换多项式,我们只需要证明:对于任意的d∈F2m,方程

f(x)=(x2+x+δ)k+x=d

(6)

在F2m中有唯一的解.由于(2m/2-2)k≡2m/2-1(mod 2m-1),因此(6)化成

(x2+x+δ)2m/2-1=(x+d)2m/2-2.

(7)

(8)

对方程(8)两侧都提升2m/2次幂得

(9)

把(8)和(9)的两侧相乘,我们得到

(10)

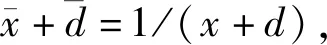
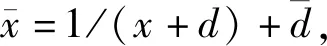
(11)

(8)和(11)相结合得到

因此

(12)

(11)与(12)比较,可得

简化得

令y=x+d,则

(13)

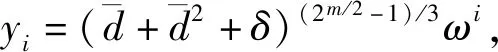
定理3设δ∈F2m且Tr(δ)=1,k|m,m/k是奇数,那么对于任意满足 (2k+1)k′≡1(mod 2m-1) 的正整数k′以及a∈F2k,均有f(x)=(ax2k+ax+δ)k′+x是F2m上的一个置换多项式.

证明当a=0时显然成立,下面假设a≠0.由于gcd(k,m)=k,并且m/k是奇数,gcd(2k+1,2m-1)=1.那么x2k+1是F2m上的一个置换多项式.对于任意的d∈F2m,我们将证明f(x)=(ax2k+ax+δ)k′+x=d在F2m中有唯一的解.由于Tr(δ)=1,对于所有的x∈F2m,因此ax2k+ax+δ≠0.方程f(x)=d等价于

(ax2k+ax+δ)k′=x+d.

进一步等价于

ax2k+ax+δ=(x+d)2k+1.

即

x2k+1+(d+a)x2k+(d2k+a)x+d2k+1+δ=0.

因为a∈F2k,所以我们有a2k=a,即x2k+1+(d+a)x2k+(d+a)2kx+d2k+1+δ=0.公式等价于

x2k+1+(d+a)x2k+(d+a)2kx+(d+a)2k+1=δ+d2ka+a2kd+a2k+1.

即

(x+d+a)2k+1=δ+d2ka+a2kd+a2k+1.

由于x2k+1是F2m上的置换多项式,那么存在唯一的x∈F2m满足上述方程.因此f(x)是F2m上的一个置换多项式.

定理4设δ∈F2m且Tr(δ)=1,如果m和k均为正偶数且m/gcd(k,m)是奇数,那么对于任意满足(2k+1)k′≡2m/2-1(mod 2m-1) 的正整数k′以及任意的a∈F2m/2,均有f(x)=1/(ax2k+ax+δ)k′+x是F2m上的一个置换多项式.

证明当a=0时显然成立,下面假设a≠0.由于m/gcd(k,m)是奇数,gcd(2k+1,2m-1)=1.那么我们有x2k+1是F2m上的一个置换多项式.对于任意的d∈F2m,我们将证明f(x)=d在F2m中有唯一的解.由于Tr(δ)=1,对于所有的x∈F2xm,x2k+x+δ≠0.方程f(x)=d等价于 1/(ax2k+ax+δ)k′=x+d.

进一步等价于

1/(ax2k+ax+δ)2m/2-1=(x+d)2k+1.

(14)

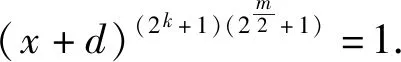
x2m/2=1/(x+d)+d2m/2.

(15)

由于x≠d,那么我们由方程(14)(15)可得

ax2k+ax+δ=(x+d)2k+1(ax2k+ax+δ)2m/2=(x+d)2k+1a2m/2((1/(x+d)+d2m/2)2k+(1/(x+d)+d2m/2)+(δ/a)2m/2)=

a2m/2(x+d+(x+d)2k+(x+d)2k+1((δ/a)2m/2+d2m/2+k+d2m/2))=a2m/2(x+d+x2k+

d2k+(x+d)2k+1((δ/a)2m/2+d2m/2+k+d2m/2)).

因为a∈F2m/2,我们有a2m/2=a.化简上式可得

(x+d)2k+1=(δ+ad+ad2k)/(δ2m/2+a2m/2d2m/2+k+a2m/2d2m/2)=(δ+ad+ad2k)1-2m/2.

对于固定的δ,a和d,x2k+1是F2m上的一个置换多项式,那么方程(14)有唯一的解.这就证明了f(x)是一个置换多项式.

定理5设δ,a∈F2m,m,k,s均是正整数,满足gcd(m,k)>1,s(2k-1)≡0(mod 2m-1),那么f(x)=(ax2k+ax+δ)s+x是F2m上的一个置换多项式.

证明当a=0时显然成立,下面假设a≠0.多项式f(x)是一个置换多项式,当且仅当对于任意的d∈F2m,

(ax2k+ax+δ)s+x=d

(16)

在F2m中有唯一解.由方程(14)我们得到

(ax2k+ax+δ)j(2m-1)=(x+d)2k-1,

(17)

(a(d+α)2k+ad+α+δ)s+x=α.

(18)

由α2k+α=0,方程(18)简化成(d2k+d+δ)s+x=α,并且

x0=d+(d2k+d+δ)s=d.

(19)