含植物河道等效床面阻力试验研究

高学平，吕建璋，孙博闻，刘殷竹

（天津大学水利工程仿真与安全国家重点实验室，天津 300350）

1 研究背景

植物广泛存在于天然河道、滩地、湿地，可起到净化水质、稳固边坡的作用［1］，在水生态系统中发挥着重要作用。与此同时，植物的存在改变了水流结构［2-6］，增加了水流阻力［7-9］。一般地，运用力的平衡原理，在同样来流条件下原床面（无植物床面）阻力的基础上，将植物阻力均匀作用在床面上，共同构成含植物河道等效床面阻力［10］，这时需要获得等效床面阻力来预测水位及流速分布，从而在保证河道过水能力和改善水环境之间寻求平衡。

计算植物阻力是获得等效床面阻力的重要一环，植物阻力与水流条件（流速、水深等）、植物物理特征（高度、茎杆直径、刚度、叶面积等）、植物密度等诸多因素相关。对于刚性植物，许多学者使用圆柱杆代替［11］，变化布置密度及水流条件等，对其拖曳力系数CD进行了研究［12-16］。对于柔性植物，植物随水流发生弯曲和结构变形［17］，增加了问题的复杂性。很多学者采用塑料纤维［18］、聚乙烯薄片［19-20］、仿生植物等［21］代表柔性植物进行试验。Vogel［22］引入指数b，提出植物阻力Fv～uv2+b，b因植物种类而异。Whittaker等［23］考虑了植物的抗弯刚度EI，使用改进的柯西数方法来预测柔性植物的阻力系数。Järvelä［24］和Jalonen 等［25］使用叶面积指数（LAI），即单位床面面积上的叶面积代替正投影面积，提出了预测特定植物阻力系数fv的计算方法。淹没情况下，水流可分为植物层和自由水层，植物和原有床面可以视为统一床面处理，进而方便了含植物水流水力特性［26-28］和阻力特性［29-30］的研究，郑爽等［31］通过含淹没柔性水生植物水流的水槽试验和量纲分析，得出了等效床面糙率经验公式。非淹没情况下，断面平均流速相同时，水深变化，植物受力变化，从而等效床面阻力随着水深的变化而变化，Wang等［32］建立了等效床面阻力系数与CD之间的关系，许多学者通过试验和数值模拟的方法对非淹没情况下植物拖曳力系数CD进行了深入研究［33-35］。

实际应用中，最常以等效床面糙率表征等效床面阻力。吴乔枫等［36］基于植被分布将河道断面划分为若干糙率不同的子区，人工率定了各分区的糙率，进而反演了糙率-水位曲线。唐洪武等［10］基于力的平衡，采用圆柱铝棒进行了试验，得出了等效床面糙率，并提出了一系列等效水力参数概念。Phillips 等［37］直接根据床面特征及粗略的植物描述，选取等效床面糙率。Wang 等［38］将11 种含植被等效床面糙率计算方法耦合于HEC-RAS中，对其适用性进行了评价，与人工校正曼宁系数的原始模型相比，根据植物阻力动态调整糙率的模型对于大流量下的河道水位等预测更准确。

然而，以往对于含植物水流阻力的研究，植物多采用替代品，水流条件虽然可以缩比尺，但替代品与实际植物并不相似，从而还原不到真实的情境中，诸如水面坡降、水流水力特性等刻画不够准确，成果只可部分指导实际。同时，含植物河道等效床面糙率大多都根据经验选取，或者在数学模型中人工校正，抑或是在实验室尺度根据植物替代品得出，根据真实植物阻力变化动态调整等效床面糙率的研究不够完善。

基于上述不足，本文选用3 种典型的真实植物进行水槽试验，植物布局参照现场调研的结果选取，根据植物所处实际河道的不同位置施以对应的真实流速条件，量测各试验工况的水面线及流速分布。将等效床面阻力分解为植物阻力和同样来流条件下的原床面阻力，计算植物阻力，换算得出含植物河道等效床面糙率。

2 研究思路与试验设计

2.1 研究思路含植物河道的典型横断面如图1所示。首先，沿横向和垂向对河道横断面的水体分区，对于每一分区含植物的水体进行试验。植物采用实际植物，施以实际过流时相应的流速，研究各分区植物对于水流的作用。然后，将含植物的总阻力减去相同来流条件下无植物时的阻力，得到植物拖曳力系数CD，用以表征单位高度单株植物阻力。在此基础上将各分区的植物阻力合成，得到相应水流条件下的植物阻力系数fv。最后，在获得植物阻力的基础上，将其附加于床面上，换算得到植物等效附加糙率nv，进而求得等效床面糙率n′b。

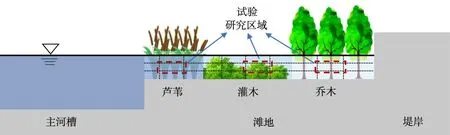
图1 含植物河道横断面及分区

2.2 试验装置试验在天津大学水利馆进行，试验水槽系统如图2所示，水槽全长28 m、宽2 m、高0.9 m，底坡为0，水流经输水管道和稳水栅平顺地流入水槽，经可调节水位的栅格式尾门流出，系统最大流量500 L/s。流速测量采用声学多普勒流速仪（ADV），水位测量采用水位测针，精度为0.1 mm，流量测量采用尾门下游的矩形薄壁堰。其中，试验段总长12 m，铺设20 cm厚的石子作为床面，中值粒径D50=1.0 cm，试验段的上、下游各铺设坡比为1∶5的斜坡，使水流较平顺地流入和流出试验段。

图2 试验水槽系统

定义x方向为水流方向，y方向为横向，z方向为垂向，试验段上游边缘对应x=0 m，水槽右边壁对应y=0 m，试验段石子层表面对应z=0 m。在试验段设置了11 个水面线测量断面（起始断面为x=0.75 m，断面之间间隔1.05 m）。

注：A为无植物组试验；B为乔木组试验；C为灌木组试验；D为芦苇组试验；Re为雷诺数，Re=ucR/ν，uc为控制断面平均流速，R为水力半径，ν 为运动黏滞系数；Fr为弗劳德数，，h为水深；尾门最小开度、控制断面平均流速为0.2 m/s时，最大水深为0.55 m。

2.3 试验方案以天津市重要的行洪河道独流减河为研究对象，采用的植物均为河道主槽和滩地中的典型植物。植物布置密度基于现场调研结果，且流速条件满足各特定植物区域的实际流速。试验分为含植物组和不含植物组。无植物组试验和含植物组试验共计53组，设计试验工况列于表1，水流条件均为紊流，工况A1代表控制断面水深0.6 m、控制断面平均流速0.4 m/s 的无植物组试验，其余同理，控制断面位于1#水面线测量断面。试验测量了各试验工况11个水面线测量断面的水深，每个断面测3次水深取平均。

量测典型断面流速分布，按图3所示的流速测线沿垂向均匀布设测点，每个测点量测60 s，采样频率为50 Hz。

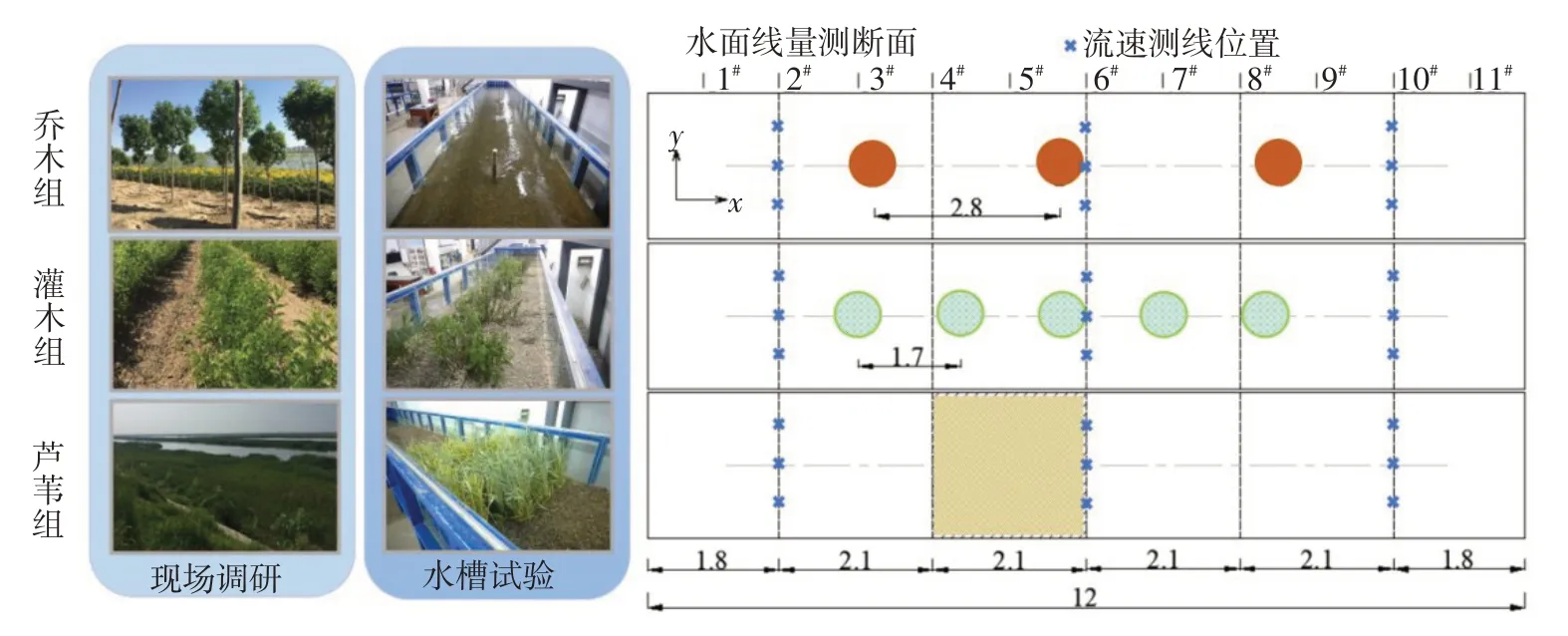
图3 试验水槽中植物布置及对应的现场调研情况（单位：m）

含植物组的试验有乔木组、灌木组、芦苇组，所有植物均取自现场，裁剪后所有植物高度hv均为65 cm。试验水槽中植物布置及对应的现场调研情况如图3所示。水槽宽度为2 m，与现场调研的乔木及灌木品种沿河宽方向的行距相近，植物沿水流方向的株距同现场一致，试验结果可适用于独流减河滩地上布置对应植物的整片区域。等效床面的宽度B0取为2 m，等效床面的长度L与株数、株距有关。等效床面面积等于植物株数、株距、行距三者的乘积。所采用乔木品种为槐树，是独流减河滩地常见的乔木，布置间距为2.8 m，共布置了3棵，等效床面覆盖的区域为2 m×8.4 m（水面线测量断面2#～10#之间），直径为6 cm，不考虑分枝和叶片。所采用灌木品种为紫穗槐，是独流减滩地常见的灌木，布置间距为1.7 m，共布置了5株，等效床面覆盖的区域为2 m×8.4 m（水面线测量断面2#～10#之间），每株灌木平均有20根直径为8 mm的分枝，每根分枝上约有200片4 cm×1.5 cm的叶片。芦苇杆直径为4 mm，平均每根65 cm 高的芦苇杆有4 片35 cm×2 cm 的叶片，种植密度为250 根/m2，等效床面覆盖的区域为2 m×2.1 m（水面线测量断面4#～6#之间）。

3 试验数据处理方法

依据试验数据得到研究区域的平均流速和水力坡降，计算得到分区阻力，将各分区的植物阻力合成，得到实际河道相应水流条件下的植物阻力系数fv，换算得到植物等效附加糙率nv，进而求得等效床面糙率。对含植物组而言，研究区域对应植物等效覆盖区域。

研究区域的平均流速uv可由下式确定：

式中：Q为试验流量，m3/s；为研究区域的平均水深，m；B0为研究区域的宽度，m。

研究区域的水力坡降可表示为：

式中：hi为第i个断面的水深，m；ui为第i个断面的平均流速，i=1代表研究区域上游断面，i=2代表研究区域的下游断面；x代表研究区域纵向长度，m。

各试验工况均为渐变流，近似作为均匀流进行处理，结合曼宁公式，综合糙率n可由下式确定：

根据水力半径分割法［39］，综合糙率n也可表示为：

式中：nb为床面糙率；nw为水槽两侧边壁糙率；χ为湿周，m。

含植物组床面阻力减去无植物组床面阻力得到植物阻力，植物阻力大小与水槽两侧边壁糙率无关，依据水槽壁面材料本文试验取为常数0.01。试验求解等效床面阻力时，植物阻力只附加于床面上，床面糙率剔除了水槽两侧边壁的影响。

根据式（3）和式（4），可求得床面糙率nb。

结合达西-魏斯巴赫公式，可得：

式中：fb为原床面阻力系数；f′为等效床面阻力系数；nb0为原床面糙率；n′b为等效床面糙率。

将植物阻力均匀分布在床面上，阻力系数可直观反映等效床面阻力各部分，根据阻力系数的可加性，植物阻力系数fv可表示为：

在试验基础上建立植物阻力系数fv和拖曳力系数CD之间的关系，将各分区的植物阻力合成，得到实际河道相应水流条件下的植物阻力系数fv。植物等效附加糙率nv与水深h有关，非淹没和淹没情况下植物等效附加糙率的计算有所区别。

非淹没时，应用均匀流公式可得：

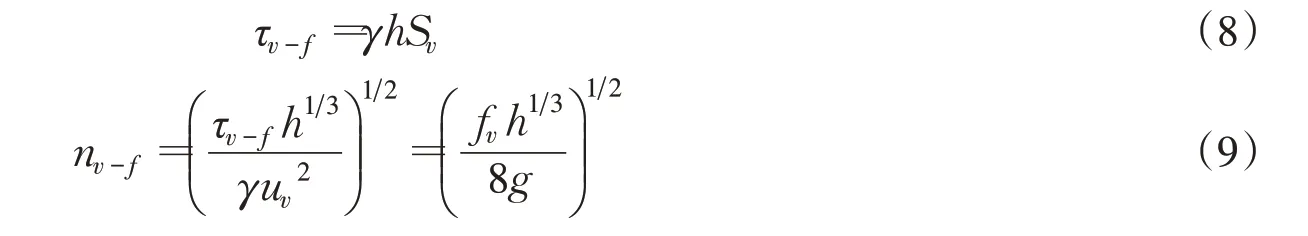
式中：τv-f为非淹没时的植物等效切应力；Sv为植物存在时的水力坡降与相同来流条件下无植物时水力坡降的差值；nv-f为非淹没时的植物等效附加糙率。

当h=hv时，植物刚淹没，这时的植物等效附加糙率nv0可由下式计算得到：

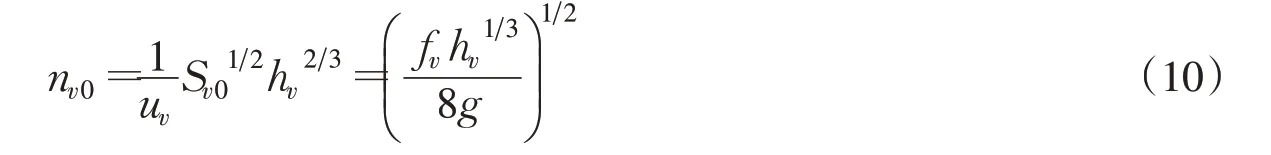
式中Sv0为刚淹没情况下植物存在时的水力坡降与相同来流条件下无植物时水力坡降的差值。

淹没情况下的植物等效附加糙率nv-y可表示为：

此时的植物等效切应力τv-y可由下式获得：

植物等效切应力比刚淹没时小，式（12）右边第二项代表植物冠层以上的水体对植物的作用。

淹没时植物上层水体对植物的作用力很小，Sv可表示为：

将式（13）代入式（12），并与式（10）和式（11）联立，可以得到：

在得到植物等效附加糙率的基础上，利用下式可得到等效床面糙率：

4 结果与分析

4.1 乔木组阻力试验成果植物阻力可由等效床面阻力减去相同来流条件下的原床面阻力得到。首先对17组无植物组试验数据进行分析，计算得到原床面阻力。原床面阻力系数fb和原床面糙率nb0与雷诺数之间的关系如图4所示。由图4可以看出，fb和nb0均随着Re的增加而减小，且随Re增长到一定程度趋于常数。

图4 原床面阻力系数以及糙率系数与雷诺数之间的关系

乔木组植物受力［32］可采用下式确定：

式中：FD为植物阻力，N；m为单位面积植株数，1/m2；Avs为单株植物茎杆迎水面的投影面积，m2；CDs为茎杆拖曳力系数。

由式（16）可得：

实际使用中，拖曳力系数可以表征单位高度植物阻力大小，由式（7）和式（17）可得乔木组CDs实测值。因为乔木组植物布置密度小，可以认为前一株植物的尾流对后一株植物影响很小，可近似视为单圆柱绕流问题。

以往研究计算单圆柱绕流拖曳力系数的公式列于表2。乔木组CDs实测值和利用表2公式计算的预测值对比如图5所示。实测值略大于预测值，这是因为乔木杆表面粗糙不平，与采用光滑圆柱杆试验相比，乔木表面的摩擦力略大于圆柱杆表面的摩擦力，这里的拖曳力系数是摩擦力和压差阻力综合作用的结果。

表2 以往研究计算单圆柱绕流拖曳力系数的公式

图5 乔木组CDs实测值与预测值的比较

4.2 灌木组和芦苇组阻力试验成果

4.2.1 典型试验工况水力特性试验结果 首先通过典型试验工况的水力特性试验结果定性说明植物阻力大小。选取表1中编号11、编号12、编号13共计9组试验工况，6#水面线测量断面中测线（x=6 m，y=1 m）沿垂向的流速分布和紊动能TKE分布分别如图6 和图7所示。图6 和图7 中的（a）代表A11、C11、D11三组试验工况，（b）代表A12、C12、D12三组试验工况，（c）代表A13、C13、D13三组试验工况。由图6可得，在相同来流条件下，水流流经植物之后，流速减小，其中芦苇组流速减小最明显，说明其对应的等效床面阻力较大。由图7可知，在相同来流条件下，水流流经植物之后，紊动能普遍增加，水流掺混更加剧烈［42］。

图6 典型试验工况6#断面中测线沿垂向的流速分布

图7 典型试验工况6#断面中测线沿垂向的紊动能分布

4.2.2 各试验工况植物阻力系数试验结果 类比式（17），可得灌木组和芦苇组的植物阻力系数计算公式：

式中：Avs和Avl分别为单株植物未发生变形时茎杆和叶的面积；CD-tot为综合拖曳力系数。

结合无植物组的原床面阻力试验成果，将灌木组、芦苇组试验测量所得的植物阻力系数fv随对应的淹没度（h/hv）的变化情况绘制于图8，hv为植物高度，h代表水深。由图8可以看出，芦苇组的fv明显大于灌木组的fv，且大一个数量级。灌木组和芦苇组的植物阻力系数基本上正比于淹没度（淹没度小于1时），这是因为试验使用的实际植物沿水深方向近似均一，相同断面平均流速、不同水深条件下，沿水深方向变形相差不大，综合拖曳力系数CD-tot比较接近。

图8 灌木组及芦苇组fv测量值与淹没度（h/hv）之间的关系

利用式（18）求得灌木组和芦苇组各工况对应的CD-tot绘于图9。从图8和图9中可以发现，断面平均流速越大，灌木组和芦苇组的越小，对应的CD-tot越小。这与对应流速条件下植物茎杆和叶的变形程度密切相关，流速越大，真实的阻水面积越小，为方便实际使用，将阻水面积的减小体现在了综合拖曳力系数中。

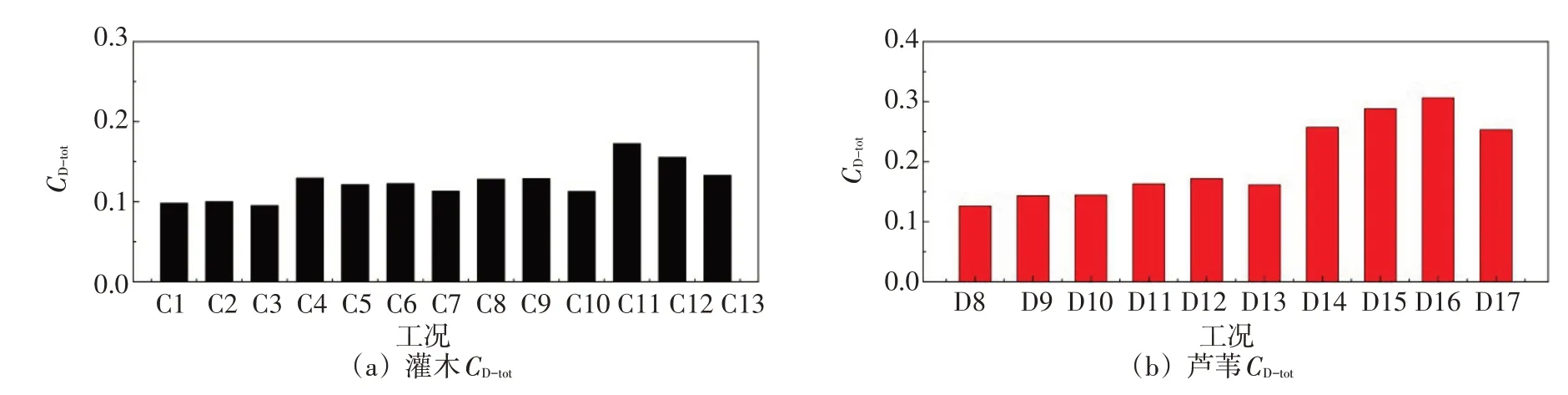
图9 灌木组和芦苇组各工况对应的CD-tot

4.2.3 植物阻力系数试验结果与以往研究的对比 以往通过仿生植物等试验计算含叶片柔性植物阻力系数的公式列于表3。植物阻力系数试验结果与以往研究计算公式预测结果的对比如图10和图11所示。结果表明，因模拟实际植物的不相似导致植物阻力系数预测值与真实值存在一定的区别。值得注意的是，对于灌木和芦苇，利用Västilä 等［43-44］的计算方法，将植物阻力分为茎杆阻力和叶片阻力，计算得到的预测值与实测值的变化规律接近，且量级基本一致。

表3 含叶片柔性植物阻力系数的计算公式

图10 灌木植物阻力系数实测值与以往研究预测值的对比

图11 芦苇植物阻力系数实测值与以往研究预测值的对比

4.2.4 基于试验结果的植物阻力系数计算公式 D9、D12 和D15 三组工况植物变形情况如图12所示，控制断面水深相同，断面平均流速从左往右依次减小。由图12可见，芦苇的茎杆可近似视为刚性杆，变形不大，而叶片阻水面积变化明显，流速越小，阻水面积越大。灌木具有与芦苇相同的规律。

图12 D9、D12、D15三组工况植物变形情况

对于灌木和芦苇而言，植物阻力系数fv可以视为由茎杆阻力系数fvs和叶片阻力系数fvl两部分组成，茎杆阻力可通过文献［15］得出，叶片阻力采用文献［44，46］的表达形式，灌木和芦苇等植物的阻力系数可由下式表示：

式中：m为单位面积植株数，1/m2；d为植物直径，m；λ为植物所占水体的体积分数；φl为叶片变形系数；uφ代表决定结构变形的最小流速，m/s，参照文献［44］取为0.2 m/s。

运用式（19）对植物阻力系数试验结果进行非线性拟合，拟合得到灌木对应的叶片拖曳力系数CDl-gm为0.150，结构变形系数φl-gm为-0.975，拟合得到芦苇对应的叶片拖曳力系数CDl-lw为0.252，结构变形系数φl-lw为-1.810。本文拟合出的叶片拖曳力系数和结构变形系数与前人采用仿生植物的研究成果［1，24，43-44，46］有所区别。植物阻力系数实测值和基于试验结果的拟合公式预测值对比如图13所示，整体的Pearson 相关系数为0.996，灌木组RMSE=0.020，芦苇组RMSE=0.325，表明拟合效果比较好。式（19）相比式（18），一旦确定了叶片拖曳力系数和结构变形系数，各流速条件下植物阻力均比较容易获得，而综合拖曳力系数CD-tot因流速而异，在实际应用中具有一定的限制。

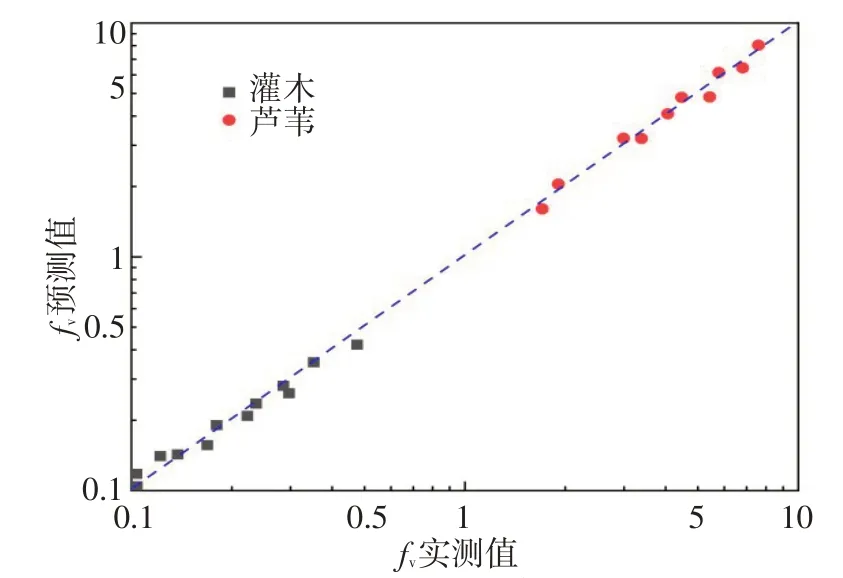
图13 植物阻力系数实测值和基于试验结果的拟合公式预测值对比

5 成果应用

以独流减河上游典型河道断面为例，具体说明成果应用。100年一遇洪水时，独流减河上游典型河道断面水位5.73 m，滩地高程2.5 m，水深3.23 m，灌木高1.5 m处于淹没状态，乔木处于非淹没状态，芦苇处于非淹没状态。植物位于河道的位置不同，流速也有一定的差异，这里给出了几组不同的流速条件。近似认为沿水深方向流速分布比较均匀，基于试验结果，运用式（9）和式（14）计算得到的独流减河上游100一遇洪水位不同流速条件下植物等效附加糙率列于表4，依据实际河道的床面情况，无植物的河道糙率取为0.025，含植物的等效床面糙率也列于表4。由表4可知：100年一遇洪水位，植物等效附加糙率相对较大，芦苇等效附加糙率结果与文献［47］采用实际植物得到的试验成果在一个量级。

表4 独流减河上游典型河道断面不同流速条件下植物等效附加糙率及等效床面糙率

值得注意的是，植物等效附加糙率只针对种植植物的河道部分，并不是针对河道全断面，采用平面二维数学模型进行数值模拟时，只需含植物的网格在无植物河道糙率的基础上增加植物等效附加糙率。独流减河上游典型河道断面及植物等效附加糙率应用如图14所示，需要局部加糙的滩地区域约占河宽的1/10。含植物河道等效床面阻力与流速有关，前人在复式河槽沿横向的流速分布［48-51］以及含植物漫滩的复式河槽水流水力特性［53-54］等方面取得了一定的成果，在此基础上可估算河道不同分区的流速，经过多次调整得到比较准确的等效床面糙率，相应的流程图如图15所示。未来仍需在不同种类植物阻力计算以及含植物河道水流水力特性等方面深入研究。

图14 独流减河上游典型河道断面及植物等效附加糙率应用

图15 实际应用含植物河道等效床面糙率调整选定流程

6 结论

本文提出了对河道植物分区施加实际流速条件进行试验的思路，针对独流减河实际植物及流速条件，进行了无植物组、乔木组、灌木组、芦苇组试验，植物密度采用现场调研结果，对含植物河道等效床面阻力进行了试验研究，得出以下结论：（1）本文沿横向和垂向对河道横断面分区，试验研究了分区水体中的植物阻力，在此基础上将各分区的植物阻力合成。在获得植物阻力的基础上，将其附加于床面上，换算得到植物等效附加糙率，进而求得等效床面糙率。利用本文方法可获得任意植物河道对应的等效床面糙率。（2）以独流减河上游典型河道断面为例，100年一遇洪水条件下，无植物河道糙率取为0.025，沿垂向的流速在0.3～0.6 m/s时，乔木种植区域的等效床面糙率为0.060～0.066；沿垂向的流速在0.3～0.6 m/s时，灌木种植区域的等效床面糙率为0.083～0.099；沿垂向的流速在0.2～0.4 m/s时，芦苇种植区域的等效床面糙率为0.698～0.989。