基于联系数的大型灌区水资源空间均衡评价与优化调控

张礼兵，喻海関，金菊良，胡亚南，崔 毅，吴成国

（1.合肥工业大学土木与水利工程学院，安徽合肥 230009；2.合肥工业大学水资源与环境系统工程研究所，安徽合肥 230009）

1 研究背景

经济社会高速非均衡发展会导致区域过度分化和各地严重失衡的利益格局［1］。进入21世纪以来，国家战略由区域非均衡发展开始逐步向总体均衡发展转变，这对保障经济社会发展和生态环境改善具有重要支撑作用的水资源管理提出了更高要求，特别是在习近平总书记就保障国家水安全战略问题提出“节水优先、空间均衡、系统治理、两手发力”的十六字治水方针以来，水科学界迅速聚焦国家发展的这一重大需求，从理论和实践出发持续开展水资源空间均衡概念内涵、技术方法及应用方面的研究。

1.1 在理论研究方面王浩等［2］初步阐述了水资源空间均衡的概念，即实现水资源系统与社会经济系统之间、不同区域之间的协调发展；郦建强等［3］认为“空间均衡”就是流域或某一区域范围内人口经济社会发展与资源环境相均衡；左其亭等［4］建议根据研究对象和目标选择的不同，将水资源空间均衡度具化为分布空间均衡度、供需平衡空间均衡度、社会经济匹配空间均衡度、调配格局空间均衡度、协调发展空间均衡度等；金菊良等［5］指出水资源空间均衡的核心是水资源系统的空间分布与经济社会、生态环境的空间分布在时间、空间上相协调相匹配的双重水资源供需平衡；游进军等［6］认为，空间均衡要求重新审视用水需求与区域经济发展、水资源约束条件之间的关系，研究以宏观供需形势分析为目标的技术方法，识别供需问题和调控方向，支撑供需总量平衡决策。

1.2 在应用实践研究方面彭祥等［7］通过构建水资源配置博弈均衡模型，利用合作博弈理论对未来黄河水资源配置提出初步制度设计；成艾华［8］运用一般均衡分析方法，从现代经济学和参与方角度建立一个包括调水区、受水区、工程方的跨流域调水市场理想化模型，从静态与动态、短期与长期探讨工程参与多方一般均衡的实现与利益分配关系；朱彩琳等［9］构建了面向空间均衡的水资源优化配置模型，其着重考虑不同空间单元之间的关系；左其亭等［10］提出表征任意空间单元均衡程度的空间均衡系数，以及表征全区域均衡程度的总体空间均衡度概念和计算方法；王煜等［11］通过构建水资源均衡调控函数来引导水资源配置，建立适用于黄河等缺水流域的水资源均衡调控方法；夏帆等［12］采用基尼系数与协调发展度的方法，基于水资源负载指数、水土资源匹配系数和用水效益计算水资源空间均衡系数，并以省级行政区为计算单元计算全国水资源空间均衡系数；杨亚锋等［13］采用可变集原理及偏联系数方法构建一种新的水资源空间均衡评估模型并对全国水资源空间均衡状况进行评价；Feng［14］采用满意度来衡量生活、农业和工业部门的水资源分配公平性，并提出一种多目标动态优化模型来优化水资源配置。

综上可见，目前水资源空间均衡研究与应用主要集中在水资源空间均衡的理论内涵、状态识别、综合评价和优化调控等方面，一般围绕水的节约高效利用、水的刚性合理需求、水的规模适度开发、水的高水平供需平衡4个方面开展［3，5］，前三者是实现水资源空间均衡目标的保障措施和管控途径，后者是水资源空间均衡的最终目标，这是因为水的供需状况及其变化是水的分布特征、开发利用、调节分配的综合体现。因此，水资源空间均衡可概化为水资源系统供需之间的均衡关系，这就方便从供给和需求两方面进行双向调节；同时水资源供需空间均衡分析将水资源分布态势与社会发展状况紧密结合，不仅能有效判断水资源与经济社会协调发展程度，也可以为水资源的合理配置提供重要依据。基于此，本文提出以供需差占供需总量之比定义水资源系统的单元供需均衡度，并以水资源单元供需均衡度为指标，综合考虑面积、经济和人口构成系统综合权重，结合水资源空间均衡等级标准和空间均衡状态标准，运用七元联系数进行水资源空间均衡程度的综合评价，并以淠河大型灌区工程实际水资源系统为例，在分析现状水平年（2018年）灌区各单元（县市）的需水量和可供水量的基础上，计算淠河灌区水资源系统单元供需均衡度，并基于七元联系数计算分析灌区有、无系统内水资源调配的空间均衡等级，再利用加速遗传算法（Accelerating Genetic Algorithm，AGA）优化现状水资源调配方案，同时开展远景规划年（2035年）灌区水资源系统的单元供需均衡度计算及系统空间均衡等级评价，最后针对性地提出改善灌区水资源空间均衡状态的优化调控方案和技术措施，为实现灌区水资源供给与社会经济发展、生态文明建设相适应，改善区域水资源系统空间均衡状态提供参考。

2 对象区域与研究方法

2.1 研究区域概况及数据来源淠河灌区位于江淮分水岭两侧，跨越长江、淮河流域，南抵丰乐河及其主要支流张店河一线，北至淮河南岸，西界淠河，东至合肥，控制面积7750 km2。灌区覆盖区域包括六安的霍山县、六安市区（金安区和裕安区），合肥的长丰县、肥东县、肥西县、合肥市区以及淮南的寿县共7个县市，是一个包括现代化大型城市2座、总人口998万、工业增加值3109亿元、有效灌溉面积41.1万hm2、农作物产量占安徽省1/6的城乡复合式大型灌区水资源系统。淠河灌区水源来自3个部分：上游骨干源头水库响洪甸、佛子岭、磨子潭和白莲崖，灌区内部上百座中小型水库和近万座塘坝堰闸，以及灌区尾部瓦埠湖和巢湖等提灌工程，上游水库供水经横排头渠首枢纽进入淠河总干渠，再经淠东、瓦西、瓦东、滁河、蜀山、潜南等干渠分别输送至上述7个县市。灌区水资源系统调水结构概化如图1所示。

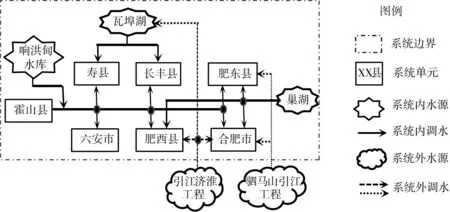
图1 淠河灌区水资源系统调水结构示意

本研究以2005—2018年淠河灌区的水土资源禀赋、经济社会发展为数据基础，以2018年为现状水平年，水资源数据主要来自《合肥市水资源公报（2010—2018）》《六安市水资源公报（2010—2018）》《淮南市水资源公报（2005—2018）》《安徽省水利年鉴（2005—2018）》等，灌区水库蓄供水量、作物耕种面积、灌溉需水量等来自《安徽省中西部重点区域及淠史杭灌区水量分配方案》《安徽省淠史杭灌区续建配套与节水改造项目（2019—2020年）可行性研究报告》等，城乡人口、工业增加值等来源于《合肥市统计年鉴（2005—2018）》《六安市统计年鉴（2005—2018）》《淮南市统计年鉴（2015—2018）》，城市绿地总面积、湖泊面积等数据来自《合肥城市总体规划（2006—2020）》《合肥城市总体规划（2018—2035）》《六安城市总体规划（2008—2030）》《淮南市城市总体规划（2005—2020）》《淮南市空间规划（2017—2035）》等。

2.2 数据分析计算根据基于水资源供需关系的水资源均衡度评价方法，需先对区域内各县市的自然社会数据进行分析、归纳和计算，以获得系统各单元需水量及可供水量，简述如下。

2.2.1 需水量计算 区域需水量主要包括生活需水、工业需水、农业需水、生态需水等4个方面，其中生活需水主要是城镇以及农村生活需水［15］；农业需水主要是灌溉以及畜牧业需水量［16］；生态需水量主要包括绿地生态环境、湖泊生态环境和河道生态环境需水量［17］。限于篇幅具体计算过程详见参考文献［15-18］。

2.2.2 可供水量计算 可供水量即水资源可利用量，是指可预见的时期内，在统筹考虑生活、生产、生态环境用水的基础上，通过经济合理、技术可行的措施，在流域水资源总量中可一次性利用的最大水量［19］。由于本研究区域属江淮丘陵地区，因地下水埋藏深、总量小而开发利用少，因此这里只考虑地表水资源可利用量，计算采用扣损法，即总水资源量扣除地表水资源量中不能利用水量和不可利用水量，加上（减去）区域的调入（调出）水量作为地表水资源可利用量［20-21］。不能利用水量主要指汛期弃水，不可利用水量指河道生态基流。本文可供水量包括单元自身可供水量、其他单元调入水量以及系统外调入水量（若有），计算式为：

式中：W河道生态基流主要考虑维持生态需水和保护河道水质的环境用水；W汛期弃水是指汛期来水减去汛期用水和水库汛期蓄水的水量。

2.3 基于联系数的水资源空间均衡评价方法

2.3.1 水资源供需均衡状态、单元供需均衡度定义及计算 如前所述，本文拟从刻画区域水资源禀赋与需求量的差异性入手来测度水资源均衡情况。水资源供需均衡状态是对水资源供需关系定性、直观的表达，如供需相等为“绝对均衡”，此种情形现实中少见，供需相差不大为“基本均衡”，供需差别明显可定义为“失衡”。由于独特的气象水文和地形地貌条件，我国大部分地区长期性或阶段性的供水不足问题较为普遍，因此目前主要采用水资源开发利用率、缺水率等指标来表征区域水资源供需不平衡程度。而对于水量丰沛地区或水量过多年份造成水资源开发利用不充分，甚或引发洪涝灾害问题，目前尚没有相应统一的水资源指标加以描述。笔者认为，只有同时考虑缺水（可供水不足）和余水（可供水丰沛）方可全面刻画区域水资源均衡问题，因此将失衡状态中的需大于供称为“缺水失衡”，供大于需则为“余水失衡”。结合失衡程度的轻、中、重描述需要，本文把区域水资源系统供需均衡状态分为7种：重度缺水失衡、中度缺水失衡、轻度缺水失衡、供需基本均衡、轻度余水失衡、中度余水失衡和重度余水失衡。

单元供需均衡度是对水资源系统各单元供需均衡状态的定量刻画，即对需水量与可供水量的相对关系作无量纲化处理。目前常用的直线型无量纲化方法有阀值法和规格化法。阀值法是指标实际值与该指标的阀值相比较，如果阀值确定的太大，此法评价值对指标变化的反应就会很迟钝，如果阀值太小，就会导致评价值过于灵敏而变化剧烈。规格化法也称为极差正规化，就是以每个指标实际值减去该指标的最小值，再除以最大值与最小值的差，该法实际上是求各种评价指标实际值在该指标全距中所处位置的比例，但在非系列数据中一般没有极值或人为经验设定极值，致使不同地区和部门指标极值不同，因此方法缺乏可比性和通用性。鉴于此本文提出基于供需关系的单元均衡度量化指标：

式中：D单元为水资源单元供需均衡度，其值若大于零或某较小正值表示单元余水失衡，小于零或某较小负值表示单元缺水失衡，等于零或在零附近表示单元供需绝对均衡或基本均衡；W可供水为单元可供水量；W需水为单元需水量；W供需水总量为W可供水与W需水之和。

本文提出的水资源供需均衡度的计算方法相较于以缺水率、水资源开发利用率作为水资源均衡评价指标的传统方法具有以下特点：（1）能同时刻画缺水地区（或缺水时段）供水不足程度和丰水地区（或丰水时段）水资源富余程度；（2）开发利用率、缺水率等指标对于不同区域由于水资源禀赋不同导致差别太大而可比性差，本法可以利用一定时间段内（年或月）供水量和需水量的总体规模与水量供需差之间的关系综合反映供需平衡状态，供需总体规模类似于国家进出口贸易总额，可以直观反映内外贸易量的总体大小。该方法能严格保证均衡度变化范围处于［-1，1］而更具普适性。由于水资源空间均衡状态是在一定区间小范围变化可以认为相对稳定，因此本文定义了7种均衡状态、代表色块及相应单元供需均衡度如表1所示。

表1 水资源系统单元供需均衡度及空间均衡等级评价标准

2.3.2 系统空间均衡等级定义与评价 水资源供需均衡是指一定区域的可供水资源量（包括自产水量和调入水量）与区域内不同单元的需水量的平衡程度，包括系统内部各单元的供需平衡程度以及单元之间的均衡协调程度。水资源自然分布差异性导致区域各单元供需均衡度有好有差，系统内各单元之间和系统外水源的水量调配可以改变单元供需均衡度进而影响到系统总体空间均衡状态，但这不是简单的水量线性叠加，还要受到区域水利工程静态供水能力和供需水量动态变化的制约。笔者认为系统空间均衡程度的计算不应是各单元可供水量之和与需水量之和的比较，而是各单元供需均衡度在自然和社会等多维尺度上的耦合，是一个高维复杂系统的综合评价问题。因此，本文开展的水资源空间均衡评价是以系统各单元水资源单元供需均衡度为指标，以各单元的面积、经济（GDP）、人口占比为指标综合权重，结合空间均衡等级标准和空间均衡状态标准进行的系统综合评价。

针对上述复杂水资源系统的多维综合评价问题，本文拟采用七元联系数进行分析计算，技术路线如图2所示。由于联系数的关系结构特征能把定性定量相结合、统一处理含有随机性、模糊性、中介不确定性、未确知性等多种不确定性问题，可从同异反宏观层次、差异度项不断分解的微观层次开展有关水资源确定性与不确定性的联系和转换分析，得到的分析结果能较好地符合研究问题的实际情况［22］。因此，本文以上述各单元水资源供需均衡度作为水资源空间均衡的评价指标，将其与灌区水资源空间均衡评价等级标准构成一个集对，构造七元联系数以分析二者之间的同异反联系，从而综合评价计算各种情景下水资源系统的空间均衡等级。

图2 本研究技术路线

七元联系数是在现有集对分析理论的基础上［22-23］，进一步细化评价指标与评价等级间的差异性分析，得到更加细致评价结果的一种数学计算方法，其表达式为：

式中：u为七元联系数；a为集对系统的同一度联系数分量；b1、b2、b3、b4、b5为集对系统的差异度联系数分量；c为集对系统的对立度联系数分量；I1、I2、I3、I4、I5为差异度系数；J为对立度系数，取值范围为［-1，1］，根据均分原理I1可取2/3，I2为1/3，I3为0，I4为-1/3，I5为-2/3。

用集对分析构造样本i的第j个指标值xij与评价等级g之间的单指标联系数uijg，当指标为正向指标，即指标值越大，其对应的评价等级也越高时，其计算方法见图3。

图3 单指标联系数计算方法

图中sgj（g=0，1，2，3，4，5，6，7）为第j个指标水资源均衡度等级1、2、3、4、5、6、7的界限值。

样本值xij隶属于评价等级g的相对隶属度为［24］：

对式（5）归一化处理可得样本i指标j的单指标联系数分量vijg为［23］：

样本i的联系数分量为：

式中：nj为隶属于评价等级g的指标个数；wj为指标j的权重。

由式（7）得样本i的水资源空间均衡评价指标值联系数：

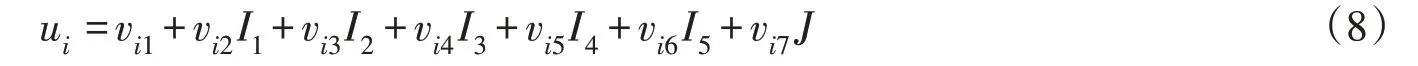
利用级别特征值法［24］求得样本i的水资源空间均衡评价等级值为：

这里水资源系统空间均衡评价等级设定为1—7级（见表1），分别对应水资源空间均衡状态的重度缺水失衡、中度缺水失衡、轻度缺水失衡、基本均衡、轻度余水失衡、中度余水失衡和重度余水失衡，也即评价等级越靠近4级，水资源空间均衡状态趋向均衡。

2.4 灌区水资源空间均衡优化调控方案的确定

2.4.1 目标函数及调控变量 本文主要通过对灌区内不同单元的水资源进行合理调配以及从灌区外进行多水源调水，改善和促进灌区各单元水资源的供需均衡，从而提升灌区整体的水资源空间均衡等级和均衡状态。考虑到淠河灌区7个县市区域位置及供用水情况将之分为3个片区：霍山县位于淠河灌区上游，来水丰富且有3座大型水库而用水量少，定义为水源区；六安市区与合肥市区分别位于灌区首尾部平原地带，城市化进程快，经济发展迅猛，定义为城市区；寿县、长丰县、肥西县、肥东县为粮食主产县的农业区。霍山县作为水量调出区，其它县市皆因自身蓄水能力弱而需水量较大均为水量调入区。外部水源是已建的驷马山引江水利工程和预计2023年建成的引江济淮工程。调控目标是使水资源空间均衡状态接近供需基本均衡，即评价等级越靠近4 级越优，目标函数构造如式（10）所示。

式中：F为灌区水资源空间均衡等级与绝对均衡值（4级）的差值，F值越小，表明灌区水资源空间均衡状态越好；hi为第i种调配水方案下灌区水资源系统空间均衡等级评价结果；优化调控变量为ΔWjk和ΔWjl，前者为灌区内第j个用水单元（j=1～7表示7个县市）从第k个供水单元（k=1，2分别表示霍山县和响洪甸水库）的受水量，后者为第j个用水单元从灌区外第l个水源（l=1，2分别表示引江济淮和驷马山引水工程）的受水量。

2.4.2 约束条件与优化方法 由调控目标函数和调控变量可知，灌区水资源空间均衡评价结果主要与灌区内水资源调配以及灌区外水源调配有关，因此在制定优化调控方案时受到灌区内各单元的需水量、可供水量、可调水量，以及单元之间水利工程的输配水能力等约束，本文采用AGA［25］优化系统内各县市调配水量和系统外调水量，限于篇幅不再详细介绍。

3 结果与讨论

3.1 现状水平年灌区水资源空间均衡评价及系统内优化调控

3.1.1 单元供需均衡度计算 根据淠河灌区现状水平年自然社会数据及2.2.1节需水量计算方法可得淠河灌区各县市需水量、见表2。

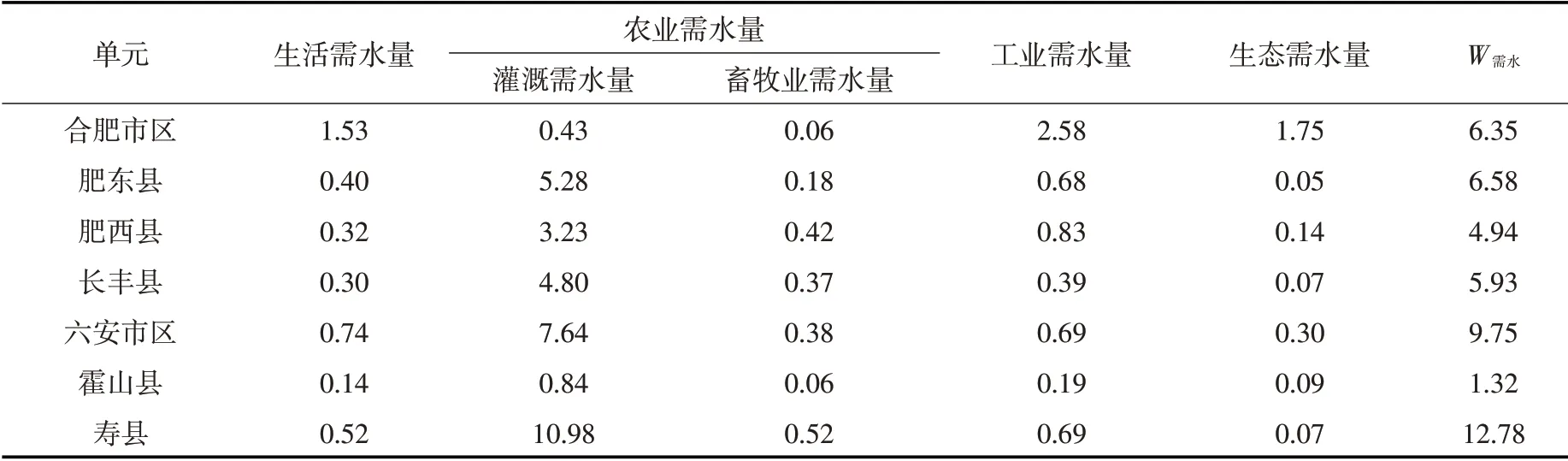
表2 现状水平年淠河灌区各县市需水量（单位：108m3）

采用式（1）、式（2）计算淠河灌区各县市可供水量，根据淠河灌区逐月来水资料及对淠河灌区汛期划分等已有的研究结果［26］，将5—8月定为汛期，汛期平均径流量约占年均径流量的55%。现状水平年灌区可供水量计算及当年实际调水情况如表3所示。

表3 现状水平年淠河灌区各县市可供水量（单位：108m3）

将上节计算得到的各县市水资源单元供需均衡度作为评价指标，同时考虑各单元的行政面积、经济（GDP）、总人口等比重确定各县市的综合权重，结果见表4。

表4 淠河灌区水资源空间均衡评价指标权重

根据现状年水量实际配置的结果可知，灌区系统内调水总量为7.42×108m3。根据式（3）对淠河灌区有、无系统内水资源调配情况下各县市水资源单元供需均衡度进行计算，结果见图4（a）（b）。图中纵坐标为淠河灌区各县市单元供需均衡度绝对值，横坐标为各县市综合权重的累加值，自左向右根据单元供需均衡度绝对值从高到低排列。

图4 现状水平年淠河灌区各单元水资源供需均衡度计算结果

由图4（a）可知，在灌区无系统内水资源配置的情况下：长丰、肥西、肥东、寿县等4个县域水资源供需均衡状态为中度缺水失衡；六安市区处于轻度缺水失衡；而合肥市区与霍山县分别处于重度缺水失衡和重度余水失衡，两地水资源余缺剧烈程度对比明显。为缓解各地水资源不均衡程度，灌区管理总局进行了系统内水资源配置，各单元供需均衡度如图4（b）所示。结果可见各县市的水资源均衡度均有明显改善，其中提升最为显著的是调入水量最多的合肥市区，说明灌区为政治、经济和文化中心的省会城市提供了重要的水资源支撑作用。

值得一提的是，图4除了能直观反映淠河灌区各县市单元供需均衡度，还可大致刻画灌区水资源系统的空间均衡状态，各县市柱状图面积和占1×1单位面积比能够反映系统空间不均衡程度，即图中柱状图面积和变化范围为［0，1］，越小表示系统空间均衡状态越好（面积和为零则为绝对均衡），反之则越差。由图4（a）和图4（b）对比可知，通过系统内的水资源调配后各县市柱状图面积和显著减小，说明水资源系统空间均衡状态明显改善。

3.1.2 系统空间均衡等级评价 为保证评价基准的一致性，本文给定s0—s7分别为-1、-0.5、-0.2、-0.05、0.05、0.2、0.5、1，且各指标的等级界限值均相同。根据水资源系统内各单元权重以及等级界限值，利用式（4）—（9）采用七元联系数方法和级别特征法评价灌区有无水资源调配情况下的灌区水资源系统空间均衡等级和均衡状态，结果见表5。

表5 现状水平年淠河灌区水资源系统空间均衡等级和均衡状态评价结果

由表5可知，现状水平年淠河灌区在采用实际系统内水资源配置方案情况下，灌区水资源空间均衡等级由无配置的2.95 提升至3.21，水资源空间均衡状态亦由中度缺水失衡改善为轻度缺水失衡。为进一步提升均衡状态，这里以式（10）作为目标函数并利用AGA对水资源配置方案进行优化，获得合肥市区、肥东、肥西、长丰、六安市区、寿县的水量分配比分别为54.84%、0.69%、3.77%、7.28%、30.32%、3.1%。图4（c）显示与实际方案相比，优化方案中的合肥、六安市区作为调水重心加大了分配水量，因此单元供需均衡度提升明显，而其他受水县除长丰外供需均衡度虽稍有下降，优化后的空间均衡等级为3.42，空间均衡状态得到进一步改善（见表5）。调控结果直接说明了“系统内水优先利用”的传统水资源调配策略对于促进现代水资源空间均衡管理有着立竿见影的效果，而优化调配方案相较实际配置方案更能使灌区的水资源空间均衡状态趋向均衡，这是因为优化调配方案更倾向于将水量调入水资源空间均衡评价中所占的权重较大的缺水县市。评价结果与图4中柱状图面积变化趋势相同，也说明了七元联系数评价方法的可靠性。

需要指出的是，由水文频率分析可知现状水平年属于偏丰年份（约20%），故而通过灌区系统内水资源优化调配可使系统接近基本均衡状态，但对于平水年则情况不容乐观，若遭遇枯水年份则极为严峻，因此有必要研究该灌区系统未来不同来水下水资源空间均衡状态的可能变化及相应调控措施。考虑与新时期国家经济社会中长期发展规划同步，这里选取2035年作为远景规划年。

3.2 远景规划年灌区水资源空间均衡预测评价及优化调控

3.2.1 需水量预测 影响灌区水资源系统需水量的社会经济主要因素有人口、工业增加值、耕地面积，生态环境因素主要有绿地面积、湖泊面积，本文利用不同预测模型分析以上相关因素变化趋势，经计算分析，利用Logistic函数分析人口数量变化趋势，合肥市区逐年递增、其它县市呈波动趋势，整体增幅较小。利用灰色预测模型分析工业增加值及耕地面积变化，工业增加值均呈增长趋势，其中合肥各县市涨势较猛；合肥市区、肥西县耕地面积逐年递减，其它县市呈波动趋势，整体变化不大。绿地面积、湖泊面积参照城市中长期发展规划。农业灌溉需水以不同情景下的农业灌溉定额与远景规划年灌溉面积的乘积预测各县市农业用水。经检验，以上因素值预测结果与研究区域城市发展规划数据较为吻合。以淠河灌区各县市需水量相关因素为输入变量、各县市需水量为输出变量构建BP 人工神经网络模型。利用训练后的BP 人工神经网络模型推求规划年份的需水量，结果见表6。

表6 BP人工神经网络预测2035年需水量结果

由需水量、可供水量预测结果可知，未来淠河灌区水资源供需矛盾较为尖锐，考虑实行节水措施来优先满足灌区刚性需水要求。节水措施主要参照《国家节水行动安徽实施方案》，实施方案主要是通过控制万元工业增加值需水量、人均用水量以及提升灌溉水利用系数来减少工业、生活、农业等三方面的需水量。充分节水条件下，各县市需水量计算结果见表6。由表6可知，与现状水平年相比，因人口增长以及产业规模扩大等原因，淠河灌区整体需水量增加明显，各县市单元需水量除肥西、寿县外均有所增加，因为二者农业用水所占比重较大且远景规划年耕地面积有所减少。

3.2.2 不同情景下可供水量计算 利用历史供水资料推求多年平均来水和80%来水情景下的可供水量，结果见表7。

表7 远景规划年淠河灌区各县市可供水量（单位：108m3）

3.2.3 单元供需均衡度预测评价及多水源优化调控 根据远景规划年充分节水后需水量和不同情景下的可供水量，计算淠河灌区各县市的单元供需均衡度见表8列（5）和图5（a）（c）所示。结果可见，规划年份在不同来水情景下灌区需水量与可供水量相差较大，各县市除水源区霍山县有余水外，其余各单元均处于中度或重度缺水失衡状态，这时仅凭系统内水资源优化配置已难以保障灌区水的均衡利用，需要借助系统外水源引江济淮工程和驷马山引江工程进行系统优化调配。

图5 远景规划年不同情景下淠河灌区各县市单元供需均衡度

由已有研究知［27］：引江济淮受水区在实施后相较于无工程情况下，长江区可供水量增幅约为5%，主要包括合肥市区、肥东县、肥西县，淮河区可供水量增幅约为16%，主要包括长丰以及寿县；驷马山引江工程为6级提水，总扬程30.1 m，提水成本较高。因此本优化方案是先由引江济淮工程供水再考虑驷马山提水供水，主要供水范围为合肥市区及肥东县，两者供水比例约为2∶1［28］。驷马山引江工程作为遭遇严重干旱时的应急水源，该工程设计引水流量约为15 m3/s，每年抽水站开机320 d，每天工作20 h，供水量为3.45×108m3。考虑到水源供水成本及距离远近不同，这里优先考虑引江济淮工程调水，驷马山引江工程作为遭遇严重干旱时的应急水源。基于现状水平年系统内水资源配置方案，以式（10）为目标函数，利用AGA 优化6 个主要受水县市的淠河灌区调水量最优分配比，来提升灌区水资源空间均衡状态。经计算可得，多年平均来水情况下的合肥市区、肥东、肥西、长丰、六安市区和寿县的最优水量分配比分别为33.52%、2.36%、9.64%、12.00%、22.31%和20.17%；80%来水频率对应来水情况下，各县市最优分配比为35.67%、3.71%、30.98%、2.46%、11.95%和15.23%。结果见表8。

表8 远景规划年淠河灌区各县市水资源系统单元供需均衡度计算结果（单位：108m3）

由表8 第8、第11 和第14 列对比可知，远景规划年灌区在多年平均以及80%来水情景下，将霍山县及响洪甸水库作为灌区水资源系统内部调水水源，引江济淮与驷马山引水工程作为灌区外部调水工程进行水资源优化调配后，各缺水县市水资源供需趋向均衡，单元供需均衡度均有所好转，其中指标权重较大的合肥市区、六安市区经水资源优化调配后均衡度提升较为显著，霍山县因受引水能力限制调出水量增加不大而余水失衡状况改善有限。图5通过地图渲染直观展示了灌区各县市供需均衡度优化前后的对比情况。

根据不同情景下灌区内各县市水资源单元供需均衡度评价结果，计算灌区水资源系统空间均衡等级和评价均衡状态见表9。

表9 远景规划年淠河灌区水资源空间均衡等级评价结果

由表9可知，远景规划年淠河灌区在充分节水条件下，不考虑水资源优化调配，多年平均来水及80%来水频率情景下灌区水资源空间均衡状态分别处于中度缺水失衡和重度缺水失衡，系统空间均衡等级分别为2.75和2.38。经水资源优化调配后分别提升至3.79级和3.41级，水资源空间均衡状态达到基本均衡和轻度缺水失衡，表明水资源优化调配对于提升区域水资源空间均衡状态具有重要作用。

4 结论

以淠河灌区为研究区域，提出了基于水资源供需关系的县市水资源系统单元供需均衡度评价方法，将各县市单元供需均衡度作为评价指标，利用七元联系数度量灌区水资源系统空间均衡等级。利用上述方法对2018年淠河灌区水资源空间均衡状态进行评价，对比分析了淠河灌区优化系统内水资源调配对灌区水资源空间均衡状态的影响。在考虑充分节水措施的基础上，预测了2035年不同情景下淠河灌区有无系统内水资源调配的空间均衡等级，并利用AGA优化淠河灌区系统内水资源调配方案，对优化结果进行了评价分析，得到如下结论：（1）本文提出的单元供需均衡度，通过分析计算区域水量供需差与供需总水量的关系，能同时刻画缺水地区供水不足程度和丰水地区水资源富余程度，直观反映供需矛盾的大小，使我国不同地域的指标评价结果都有相互可比性，因此本指标具有很好的通用性；（2）现状水平年淠河灌区系统内水资源实际配置方案，虽然中度缺水失衡状态没有改变，但系统空间均衡等级由无调配的2.95提升至3.21，进行系统优化后则能改善至3.42即达到轻度缺水失衡，表明水资源合理调配可有效地改善区域水资源空间均衡状态；（3）远景规划年淠河灌区在充分节水的基础上，多年平均来水与80%来水情景下，不考虑系统内外调水时灌区水资源系统空间均衡等级分别为2.75、2.38，均处于中度缺水失衡状态，而以霍山县及响洪甸水库作为灌区内调水水源，以引江济淮工程（在建）、驷马山引水工程作为灌区外调水水源时，利用AGA优化水资源调配方案，则水资源系统空间均衡等级分别提高到3.79、3.41，即达到供需基本均衡和轻度缺水失衡状态，进一步表明水资源优化调配对于缓解水资源供需矛盾，实现水资源空间均衡具有重要意义。

综上所述，水资源空间均衡是由水资源系统与经济社会、生态环境两大系统的空间分布间在时空尺度上相匹配、协调的双重水资源供需平衡，是在科学合理的综合措施下由低向高不断提升改善的发展演化过程，更是一个全新、有价值、颇具复杂性而充满挑战的广阔研究领域。限于水平，本文基于“节水优先、空间均衡、系统治理”等新时代治水要求，初步开展了水资源空间均衡综合评价与优化调控实践探索，但仍存有不足，例如水资源系统空间均衡等级过多而给综合评价带来较大的困难，水资源调配没有经济性约束以致“两手发力”未及考虑等，这在今后的工作中有待深入研究。