基于水势差驱动出流机制的微润灌水分运动模型构建及模拟

齐 伟，张展羽，，王 策，黄明逸，刘 畅，陈 于

（1.河海大学水利水电学院，江苏南京 210098；2.河海大学农业科学与工程学院，江苏南京 211100；3.江苏省农村水利科技发展中心，江苏南京 210029）

1 研究背景

随着全球人口的不断增长、城市化工业化进程的不断推进，水资源匮乏问题日益加剧。这给灌溉农业带来了巨大挑战，要求在农业生产中不断提高灌溉水利用效率［1］，因此各种节水灌溉技术应运而生。我国水资源不足和供需不平衡等问题日益严重，发展节水灌溉尤为必要［2］。微润灌是近些年发展起来的一种新型高效节水灌溉技术，其利用微润管同时作为输水管和灌水器，通过地埋方式将水精准输送到作物根区进行灌溉。微润管是一种高分子半透膜材料，表面均匀密集分布着纳米级孔隙（10～900 nm）［3］。灌溉时水分在管内外水势差的作用下从纳米孔隙渗出，根据土壤墒情自动、连续、适时、适量地向作物根区供水［4］。与传统灌溉技术相比，微润灌具有运行费用（所需工作压力）低、地表蒸发小、抗堵塞性强、节水效果显著等优点［5-7］。

灌溉系统设计和运行管理模式极大程度上决定了灌溉水肥均匀度［8］，进而影响作物品质和产量。为优化微润灌溉技术参数从而提高其应用合理性发挥其最大效益，揭示微润灌水分入渗特征和不同因素对其影响规律则显得十分重要。近年来，国内外学者通过入渗试验或数值模拟的方法对微润灌水分运动规律进行了较多研究。张俊等［4，9］通过室内土箱试验研究发现微润灌湿润体是以微润管为轴心的柱状体，土壤质地和密度对湿润体形态影响较大，湿润锋运移距离与入渗时间呈显著的幂函数关系，土壤初始含水率对湿润锋推进速度影响显著。牛文全等［10］通过不同压力埋深下水分入渗试验发现压力水头是微润灌流量的决定性因素，微润管埋深对湿润体形状有显著影响。此外，牛文全等［11］通过田间试验验证了微润管流量随土壤含水率有一定的自我调节作用，但调节时间较短；土壤容重和初始含水率对微润管流量也有显著影响。数值模拟为不同情境下的土壤水分运动规律研究提供了实用而方便的手段。由Šimu。nek等［12］研发的HYDRUS-2D/3D模型可用于模拟水、溶质和热在多孔介质中的运移过程，目前已被广泛应用于农田土壤水分运动的研究中［13-19］。也有学者已将该模型应用于微润灌水分运动模拟。Fan等［20］计算得出微润管比流量数据后，基于HYDRUS-2D模型，将微润管考虑为定流量边界对竖直微润灌溉进行了模拟，对比实测数据验证了该模型的可靠性，并模拟分析了土壤质地、土壤初始含水率等因素对微润灌水分入渗的影响。Kanda等［1］也将微润管设为定流量边界进行了微润灌水分运动数值模拟，利用实测值验证了模型的准确性，并比较了微润灌条件下壤质砂土和砂质黏壤土两种质地土壤中水分分布和湿润锋运移的不同。而不同情境下微润管流量并不一样，所以在模型中使用定流量边界模拟需先根据试验确定其流量，这增加了模拟的难度，降低了模型的普适性。

为了构建方便有效的微润灌水分运动模型，提高模拟效率和模型适用度，本文基于微润管的水势差驱动出流机制，将管壁当作多孔介质处理来构建微润灌水分运动模型，通过试验和参数敏感性分析验证了模型的准确性和稳定性，为微润灌水分运动模拟提供了一种新的思路和方法；此外模拟分析土壤质地、微润管工作压力和埋深对微润灌水分入渗特征的影响，深入探讨影响产生的原因，分析微润灌适用条件，为微润灌溉系统的设计和管理运行等工作提供一定的理论指导。

2 材料与方法

2.1 室内试验

2.1.1 供试土样 本试验用土取自河海大学节水园区试验大田，取土深度为表层20 cm。土壤经旋耕机疏松后，过6 mm筛去除其中残留的根系及石块等杂质，然后置于通风处自然风干，风干后（质量含水率约0.054 g/g）再过2 mm筛待用。按照国际制土壤质地分类，供试土样为黏壤土。

2.1.2 微润灌土壤水分入渗试验 在室内进行微润灌土壤水分入渗试验，试验装置示意图如图1所示，主要由土箱、微润灌溉系统、数据采集系统组成。土箱由1 cm厚透明有机玻璃制作，规格为40 cm×40 cm×55 cm（长×宽×高）。土箱前后面板打有直径2 cm的对称小孔以安装微润管，后面板不同高度打有直径1 cm测量孔。

图1 入渗试验装置示意（单位：cm）

将供试土样分层均匀填入土箱，层间打毛，填土干容重为1.12 g/cm3，填土高度为43 cm。试样表面覆一层隔热膜以抑制土壤水分蒸发。马氏瓶通过橡皮管与微润管相连，模拟简易的微润灌溉系统。微润管为第三代管，四折痕双层结构。微润管长度40 cm，水平铺设于土箱内，埋深为18 cm，管内压力水头通过调节马氏瓶高度控制在100 cm。入渗过程中采用数码相机（佳能EOS 60D）拍照记录湿润锋变化，拍照时间按照先密后疏原则，并记录相应时刻马氏瓶内液面高度以计算入渗量。入渗时间设为75 h，入渗结束采用TDR测量土壤含水率。为减小试验误差，设置3个重复，试验结果取重复的平均值。采用Photoshop CS5软件对所拍湿润锋图片进行裁剪，截取试样区域（40 cm×43 cm），所对应的图像分辨率设置为1600像素×1720像素。由于试样湿润区和干燥区具有较高对比度，故直接选用魔棒工具分割湿润区和干燥区，分别使用黑白颜色填充，将其转化为黑白二值图像。最后利用Matlab R2016软件编程对二值图像进行计算，得到湿润锋数据。

2.1.3 微润管出水特性试验 为研究微润管的出水性能，进行了不同压力水头下微润管空气出流试验。将微润管置于空气中，通过橡皮软管与马氏瓶连接，调节马氏瓶高度给微润管提供不同压力水头，记录各水头下微润管出流量随时间的变化。由试验数据发现，微润管单位时间出流量与压力水头基本呈线性关系（图2）：

图2 单位长度微润管单位时间出流量与压力水头关系

式中：q为单位长度微润管单位时间出流量，ml/（h·cm）；Hm为马氏瓶提供的微润管管内压力水头，cm。

这也表明微润管单位时间出流量与沿管壁厚度方向的水力梯度成正比，管壁内部水流呈现达西流特征，因此将微润管壁当作多孔介质，采用达西定律描述其出流特征：

式中：q为单位长度微润管单位时间出流量，ml/（h·cm）；Ks为微润管饱和导水率，cm/h；φin为微润管内水势，cm；φout为微润管外水势，cm；δ为微润管管壁厚度，为0.10 cm；C为微润管横截面周长，约为4.72 cm。

联立式（1）和（2）可得微润管饱和导水率Ks=4.36×10-4cm/h。

2.1.4 土壤水力特征测定 采用定水头法测定土壤饱和导水率。采用吸力平板法测定土壤水分特征曲线，共设置8个不同吸力值，分别为0、15、30、60、100、300、600、900 cm（水柱高度）。

2.2 数值模拟

2.2.1 土壤水分运动模型 微润灌溉属于线源灌溉。管壁出水缓慢，水分沿管长度方向速度较小，同时由于本文所用管长度仅为40 cm，所以沿管方向的沿程水头损失较小，可假设微润灌出水速率沿管方向均匀分布，此外假设土壤均质、各向同性，则土壤水分运动可简化为垂直面内的二维运动问题。在直角坐标系建立微润灌土壤水分运动的数学模型，其基本方程为二维Richards方程：

式中：θ为土壤体积含水率，cm3/cm3；ψ为土壤基质势，cm；t为入渗时间，h；K( )θ为土壤非饱和导水率，cm/h。

土壤水分特征曲线和非饱和导水率采用van Genuchten-Mualem（VG-M）模型表示：

式中：θr为土壤残余含水率，cm3/cm3；θs为土壤饱和含水率，cm3/cm3；Ks为土壤饱和导水率，cm/h；Se为土壤有效饱和度，；α为进气吸力值的倒数，1/cm；n、m为经验参数，其中为孔隙关联度参数，一般取0.5。

2.2.2 水力特征参数输入 将吸力平板法测得的土壤含水率与吸力值数据导入RETC软件，使用van Genuchten 模型进行拟合，即可得到土壤的水力特征参数。Cai 等［13］在模拟陶瓷灌溉时指出灌水器的残余含水率和饱和含水率对模拟结果来说为非敏感因素，因此本文微润管的残余含水率和饱和含水率暂时分别取0.010和0.300 cm3/cm3。考虑到微润管的壁厚较小，充水后管极易饱和，故α应取较小值，取6.00×10-6cm-1。由VG模型方程可知，n值越小，介质持水性越好。微润管内孔隙为纳米级孔隙，孔径越小，越不易失水，故n应取较小值，取1.10。供试土壤和微润管的水力特征参数见表1。

表1 供试土壤和微润管VG-M水力特征参数

2.2.3 计算域、初始和边界条件 利用HYDRUS-2D/3D软件的Geometry 模块构建模拟区域。图3为模拟区域示意图。根据室内土壤水分入渗试验的布置情况，同时考虑入渗的对称性，将模拟区域设置为高43 cm、宽20 cm 的矩形区域。微润管采用内径1.5 cm、外径1.7 cm 的半圆环表示，圆环内部及附近区域网格加密。土壤初始质量含水率约0.054 g/g，换算成体积含水率约为0.060 cm3/cm3，土壤的初始吸力按0.060 cm3/cm3体积含水率对应的吸力值设置。灌溉过程中，上边界为大气边界，不考虑蒸发的影响，下边界为自由出流边界，微润管内壁为定水头边界，左边界的其他区域和右边界均为零通量边界。

图3 计算区域示意

2.3 统计分析采用平均相对误差（MRE）、归一化均方根误差（NRMSE）、纳什效率系数（NSE）3 个指标对模型模拟结果的精度进行评估，各参数表达式为：

式中：n为数据点个数，i=1，2，…，n；Mi为第i个实测值；Si为第i个模拟值；Mˉ为实测值的平均值。

MRE和NRMSE的值越接近于0，NSE的值越接近于1，则表明实测值与模拟值越接近，模型的模拟精度越高。

3 结果与分析

3.1 HYDRUS-2D模型验证选取累积入渗量、湿润锋（上，下，水平方向）运移距离和不同深度土壤平均含水率作为特征值进行模型有效性验证。图4为模型模拟值和试验实测值对比图，由图可以看出模拟值与实测值变化趋势一致。入渗前6 h内，入渗速率有随入渗时间逐渐小幅度降低的趋势，随后入渗速率几乎保持不变，累积入渗量曲线接近于一条直线（图4（a））。湿润锋在入渗前期运移速度较快，随入渗时间推移逐渐降低，并逐步趋于稳定；此外，在运移距离上上湿润锋<水平湿润锋<下湿润锋，但总体差距不大（图4（b））。入渗的水分主要集中在微润管附近，土壤平均含水率在微润管埋深处最大，随土层深度的增大或减小都逐渐减小（图4（c））。对模拟值和实测值进行统计特征分析可以看出，累积入渗量、湿润锋运移距离、土壤平均含水率的MRE和NRMSE值均接近于0，NSE的值均大于0.980，表明模型的模拟值与试验实测值吻合较好。综上，本文所建的模型精度较高，该模型模拟微润灌的土壤水分入渗过程是准确可靠的。

图4 模型模拟值与实测值对比

3.2 参数敏感性分析

3.2.1 微润管横截面形状 本文在模拟时将微润管横截面假设为理想的圆形，但实际上微润管是一种柔性材料，埋在地下会由于受到土壤围压的作用而产生变形。因此，我们改变微润管横截面形状进行模拟，以探究微润灌水分入渗对截面形状是否敏感。选取了除圆形外其他3 种具有代表性的形状，分别为椭圆形、菱形和长方形，其内圈周长保持基本一致，具体形状及尺寸见图5。模拟时微润管埋深为18 cm，压力水头为100 cm，入渗时间为75 h。变化微润管横截面形状后的模拟结果见图6，由图可以看出，不同横截面形状下的微润灌入渗量和湿润锋的值非常接近，表明在微润管截面周长一定的情况下，其形状对水分入渗的模拟结果影响较小，可以忽略不计。

图5 微润管不同横截面形状

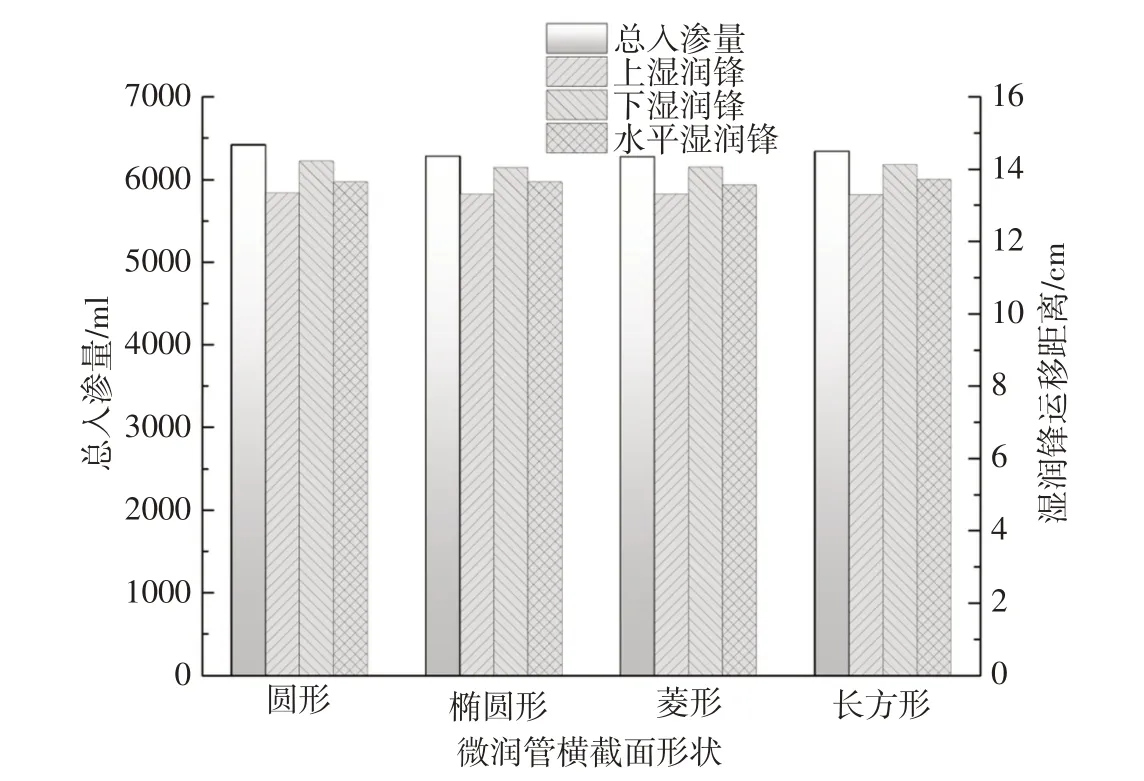
图6 不同微润管横截面形状下入渗量和湿润锋运移距离变化

3.2.2 微润管水力特征参数 由模型原理可知，模型中微润管的水力特征参数有θr、θs、α、n、Ks和l，其中Ks为试验实测值，l一般均取0.5，故只针对剩余4个参数进行敏感性分析。采用模型中的设定值作为标准参数，在合理范围内根据设定步长上下扰动。θr、θs、n以5%为步长。α由于值较小，步长为5%时变化微小，故步长设为50%。微润管埋深、工作压力和入渗持续时间设定同上。模拟发现θr和θs在上下扰动25%范围内微润灌入渗量和各方向湿润锋运移距离均保持不变，说明微润管残余含水率和饱和含水率对水分入渗几乎没有影响。这主要是因为微润管尺寸很小，入渗时极易饱和。这也一定程度上表明了前文微润管残余含水率和饱和含水率取值的合理性。α和n扰动后的模拟结果变化情况见图7。为简便起见，湿润锋运移距离只选取了水平方向湿润锋的数据。可以看出，α和n扰动下，微润灌入渗量和湿润锋运移距离变化较小，总体上表现为入渗量和湿润锋运移距离随着α值的增大逐渐减小、随着n值的增大逐渐增大，受n值扰动的影响明显大于α值的影响。这表明α和n的扰动对微润灌水分入渗影响也较小，但为提高模型精度，模拟过程中应注意提高n值的准确度。

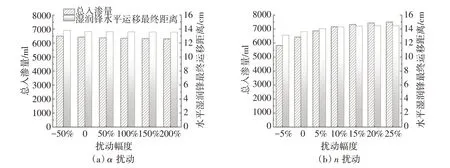
图7 微润管水力特征参数扰动下入渗量和湿润锋运移距离变化

3.3 入渗影响因素分析微润灌溉实际应用时，其土壤水分入渗特征会因为农田土壤性质、灌溉系统设计和管理的不同而发生变化，因此本文采用上述所建的模型，通过模拟分析了土壤质地、微润管工作压力和埋深对微润灌土壤水分入渗特征的影响。

3.3.1 土壤质地 选用了砂壤土、壤土、粉壤土、黏壤土4 种不同质地的土壤进行土壤水分入渗模拟。土壤的水力特征参数根据HYDRUS 软件自带的神经网络预测方法得出。土壤初始含水率设为0.15 cm3/cm3，微润管工作压力为100 cm，埋深为18 cm，入渗时间为48 h。图8为不同土壤质地下微润灌48 h后湿润体内水分分布图，可以看出，微润灌条件下水分主要集中在管附近区域，土壤含水率随着与微润管距离的增加而逐渐减小。土壤质地越黏重，管附近土壤饱和度越高，砂壤土中微润管附近土壤饱和度为0.6左右，而黏壤土中管附近土壤饱和度达到了0.92。湿润范围随土壤质地黏重性增加而减小。48 h 时，砂壤土中入渗水分已到达上下边界和右边界，壤土中水分仅到达上边界，而其余两种土壤中入渗水分未到达任何边界。壤土、粉壤土和黏壤土中的湿润体水分等值线图接近于同心圆，而砂壤土中水分下渗较明显。

图8 不同土壤质地下微润灌48h后湿润体内水分分布

图9为不同土壤质地下湿润锋运移随时间变化图。总体看来，土壤质地越黏重，湿润锋运移速度越慢。砂壤土中湿润锋运移速度明显大于其他3种土壤，且其各方向运移速度差异较大。水平向湿润锋在入渗19.5 h时达到右边界，到达右边界后上下湿润锋运移速度有所加快，分别在29 h和23 h左右到达边界。壤土、粉壤土和黏壤土中，各方向湿润锋运移距离差异不大，但实际上由于重力势的作用，运移距离为下湿润锋>水平湿润锋>上湿润锋。这3种土壤中下湿润锋运移距离与上湿润锋运移距离的比值分别为1.086，1.056，1.037，表明随着土壤质地黏重性增加，湿润锋上下运移距离差异逐渐减小，湿润范围更接近于圆形。

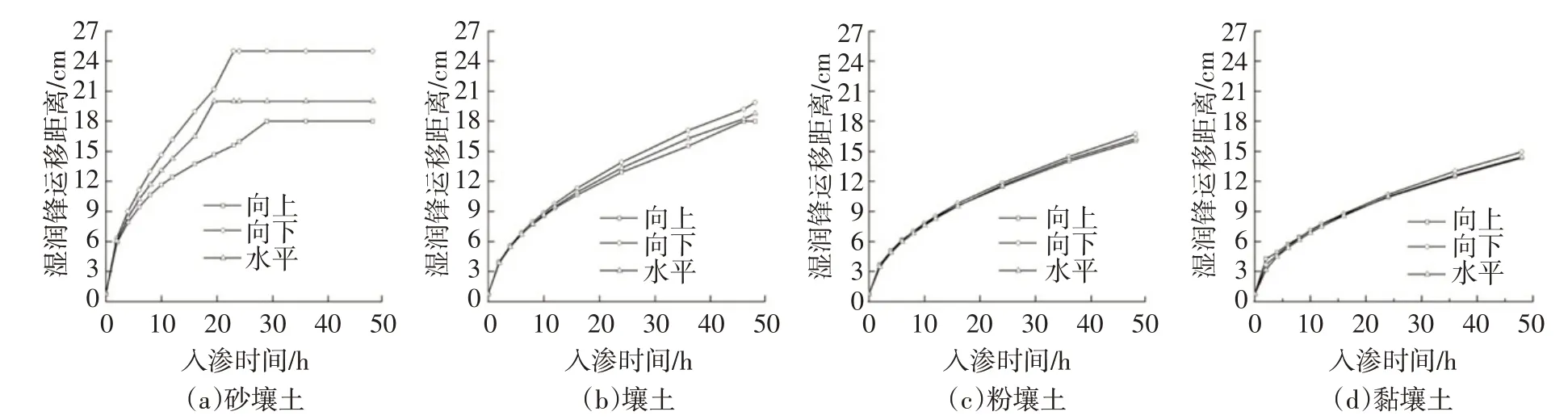
图9 不同土壤质地下湿润锋运移随时间变化

3.3.2 工作压力 选取4种压力水头（50、100、150、200 cm）进行微润灌不同工作压力水头下土壤水分入渗模拟。土壤为本文水分入渗试验所用的黏壤土，水力特征参数见表1。土壤初始含水率设为0.15 cm3/cm3，微润管埋深为18 cm，入渗时间为75 h。图10为不同工作压力下微润灌75 h后土壤湿润体内水分分布图。可以看出，不同压力水头下的微润灌湿润体在形状上差异不大，大小上差异较大。工作压力越高，湿润范围越大，且管附近土壤饱和度越大。这是因为工作压力越高，微润管内外水势差则越大，管出水速度越快，进入土壤的水量也越多。模拟区域内紧贴管外壁处土壤含水率最大，4种工作压力下灌溉75 h后紧贴管外壁处土壤含水率分别为0.55、0.54、0.53和0.50 cm3/cm3，表明土壤中均未形成饱和区。

图10 不同工作压力下微润灌75h后土壤湿润体内水分分布

图11为不同工作压力下湿润锋运移随时间变化图，由图可见，工作压力越高，湿润锋运移速度越快，这也主要是因为水势差的增大加快了微润管出水速度。比较各方向湿润锋运移距离发现上湿润锋<水平湿润锋<下湿润锋，且工作压力越高，这种现象越明显。

图11 不同工作压力下湿润锋运移随时间变化

3.3.3 管埋深 选取4 种微润管埋深（10、15、20、25 cm）进行微润灌不同埋深下土壤水分入渗模拟。土壤为本文水分入渗试验所用的黏壤土，水力特征参数见表1。土壤初始含水率设为0.15 cm3/cm3，微润管工作压力水头为100 cm，入渗时间为75 h。图12为不同埋深下微润灌75 h后土壤湿润体内水分分布图，由图可以看出，灌溉75 h后，埋深较浅的10和15 cm的模拟入渗中土壤湿润体已经达到上边界，埋深20和25 cm的模拟入渗中湿润体未到达任何边界。进一步观察其水分分布发现，埋深20和25 cm的模拟入渗中土壤水分分布几乎一致。

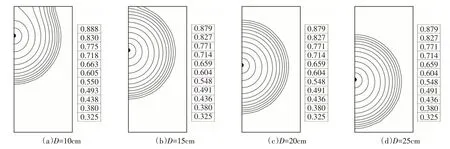
图12 不同埋深下微润灌75h后土壤湿润体内水分分布

图13为不同埋深下湿润锋运移随时间变化图。可以明显看出，在湿润锋达到边界之前，各埋深下湿润锋运移速度非常接近。由于篇幅限制，微润管出流量数据未列出，但模拟结果显示4个埋深下的微润管累积出流量基本无差异，相对差异小于0.12%。综上可以得出，微润管埋深影响湿润锋到达边界的时间，而对湿润锋运移速度和入渗量影响极小。

图13 不同埋深下湿润锋运移随时间变化

4 讨论

微润灌溉系统的设计和管理决定了其能否发挥最大效益，设计管理参数的优化需要统筹考虑微润灌入渗特征、作物耗水特点、土壤条件、气候条件等，本研究着眼于微润灌水分运动模型的构建，并采用该模型模拟了不同土壤质地、压力水头、微润管埋深下的微润灌土壤水分入渗特征，模型构建和模拟结果可为微润灌溉系统的优化应用提供一定参考。微润管作为微润灌灌水器，其表面分布着大量的微孔，水分在管内外的水势差的驱动下通过这些微孔渗出进入土壤［3］。目前在采用HY⁃DRUS-2D/3D软件进行微润灌水分运动模拟的研究中微润管大多被当作定流量边界处理［1，21］。本文室内水分入渗试验中累积入渗量随时间变化接近于一条直线（图4（a）），表明入渗过程中微润管出水流量基本恒定，实际上管出水流量随入渗进行逐渐减小并趋于稳定。在不同情境模拟中也发现微润管出水流量在入渗开始时较大，然后迅速减小，再逐渐减小趋于稳定（篇幅限制，未展示微润管出水流量数据）。牛文全等［11］通过大量田间入渗试验研究也发现微润管出水流量在入渗一段时间后减小并趋于平缓趋势。这一方面是因为入渗一段时间后微润管附近土壤含水率达到较高值，随着含水率的进一步升高其基质势变化幅度越来越小，管内外水势差变化幅度极小；另一方面，微润管壁的微孔为纳米级孔隙［3］，管出流缓慢，其出水流量对小幅度的管内外水势差变化响应不明显。因此，在管壁附近土壤含水率相对稳定的情况下，使用定流量边界模拟微润管出流是可行的。但是在实际大田条件下，由于天气（降雨、蒸发）或作物蒸腾影响，土壤含水率存在一定波动，微润管出水流量也会随之波动，使用定流量边界模拟则可能会产生较大误差，尤其在长期模拟时误差会逐渐累积，模型的准确性会明显降低。本文采用HYDRU-2D构建的模型中，基于微润管出水特性，将微润管壁当成多孔介质赋予其水力特征参数，确保其出水流量由内外水势差控制，当工作压力一定时，管壁附近土壤含水率的波动会引起微润管出水流量的变化，理论上模型的模拟结果更加合理。

不同影响因素模拟结果显示，微润灌在砂壤土中湿润面积较大，且下渗明显。这是因为砂壤土结构较疏松，颗粒间孔隙较大，渗透性强［22］，所以水分运移较快，湿润面积较大，此外，砂壤土的持水性较差，水分在运移过程中受重力势影响大，导致其下渗严重。因此，在砂性土中使用微润灌技术应当适当减小其工作压力水头和管埋深，避免产生大量深层渗漏以致灌溉水利用效率低下；而黏壤土的渗透性弱，持水性好，所以湿润面积小，水分相对更加集中在管附近。因此，在黏性土中应当适当增大工作压力水头或减小管间距以保证足够的湿润面积，避免作物需水旺盛期供水不足而影响作物品质和产量。

工作压力水头是微润灌溉系统重要的管理参数。尽管微润管作为一种半透膜材料，其出流的驱动力为管内外的水势差，出水流量可根据土壤含水率变化自动调节，但一方面由于在一般情况下管壁附近土壤含水率不会发生较大幅度和较长时间波动，另一方面由于微润管出水较缓慢，所以这种调节的幅度和时间都非常有限。因此，工作压力水头是微润管出水流量的决定性因素，也可以说工作压力水头很大程度上决定了微润灌的灌溉强度，在微润灌溉系统运行管理中可根据作物耗水强度大致确定工作压力水头的合理范围。压力水头过低则灌溉强度过小，无法满足作物需水要求，压力水头过高则湿润范围增大，易造成无效的地表蒸发和深层渗漏。在模拟不同工作压力水头下微润灌水分入渗特征时我们注意到，200 cm工作压力下，灌溉75 h后湿润锋已到达模拟区域的上边界和右边界，但此时土壤中仍未形成饱和区（图10（d）），这表明微润灌溉这种低压运行、出流较慢、依靠土壤基质吸力进行水分运移的灌溉方式，具有灌溉水分分布更加合理、对土壤通气性影响较小的优点。大量研究发现，地下滴灌条件下，滴头附近土壤常常因为灌水形成持续的饱和湿润区［23-25］，而作物根系往往优先向含水率高的滴头附近生长［26］，因此地下滴灌下作物根系常常会因为土壤通气性不佳而受到低氧胁迫，导致其品质和产量下降［23，27］。

微润管埋深是微润灌溉系统重要的设计参数。模拟结果显示，管埋深对微润管湿润锋位置有明显影响，很大程度上决定了湿润锋达到上下边界的时间。这也表明，在地表蒸发强度较大的地区，在满足作物需水的前提下，可适当增大微润管埋深，以避免大量水分到达地表造成地表蒸发损失。此外，模拟结果还显示，微润管埋深对管出流和湿润锋运移速率无明显影响。不同埋深处理对微润管管壁处土壤含水率（土壤基质势）无影响，因此入渗过程中各处理管内外水势差基本相同，微润管出流以及湿润锋运移也基本无差异。Siyal等［28］在对地下黏土管灌水分入渗进行模拟研究也发现了类似的规律。但牛文全等［10］通过室内土壤水分入渗试验发现随着微润管埋深（不包括0）的增大，累积入渗量（微润管累积出流量）呈逐渐减小的趋势。这可能有以下两点原因：（1）埋深增大，土壤容重可能随之增加，而容重增加会减小孔隙体积和增大入渗气相阻力［29］从而减小微润管出水流量［11］；（2）埋深增大，土壤压力也随之增大，导致微润管变形严重。本文2.2节敏感性分析中对不同微润管形状下水分入渗进行了模拟，结果显示微润管形状对微润灌水分入渗影响较小，但是模拟中未考虑微润管变形对其出流能力的影响。微润管的变形是否影响其内部纳米孔结构形态从而影响其出流能力，这需要进一步的研究。

5 结论

本文基于微润管出流特性构建了微润灌土壤水分运动HYDRUS-2D 模型，并研究了不同影响因素对微润灌土壤水分入渗的影响规律。主要结论如下：

（1）将微润管壁当成多孔介质处理，赋予其水力特征参数来构建微润灌水分运动模型是合理可行的，模型能较好地模拟微润灌下水分入渗特征。

（2）模型模拟结果对微润管的形状及其水力特征参数的敏感度较低。相比之下，n值对模拟结果影响稍大，需注意其取值。

（3）土壤质地越黏重，微润灌溉湿润范围越小。持水性差的土壤中水分下渗较明显。工作压力水头越高，湿润范围越大，且管附近土壤饱和度越高，但200 cm工作压力水头下不易达到饱和。微润管埋深显著影响湿润体位置，但对微润管出流量和湿润锋运移速率影响极小。

本文的模型中微润管导水率设定为恒定值，这可能与实际情况存在一定误差，后期需研究微润管形变对其出流能力的影响规律，进一步完善该模型，提高其合理性与实用性。