双吸离心泵泵站压力脉动与振动特性现场试验研究

张世杰，靳发业，姚志峰，2，王福军，2，肖若富，2，何成连

（1.中国农业大学水利与土木工程学院，北京 100083；2.北京市供水管网系统安全与节能工程技术研究中心，北京 100083；3.中水北方勘测设计研究有限责任公司，天津 300222）

1 研究背景

双吸离心泵泵站流量大、扬程高、检修方便，在大型调水工程、农田灌溉和城镇供水等重要领域应用广泛［1-2］。目前在建和新建的大型泵站中水泵单机功率不断攀升，其面临的运行稳定性问题更加突出。振动是衡量泵站运行稳定性的重要指标之一，泵内水力激振力可能诱发泵系统振动超标，结构共振，甚至致使泵站建筑结构发生破坏。复杂水力激振是诸如水泵等旋转机械中无法避免的问题，是多因素共同作用的结果。其中，动静干涉效应是最常见的水力机械水力激振源之一。

动静干涉效应［3-4］是由于叶轮出口流动不均匀（“射流-尾迹”）和压水室结构不对称共同作用的结果，其产生的压力脉动频率通常为叶频以及其倍频。叶轮叶片尾部“射流-尾迹”通常会使叶轮和压水室（或叶轮和导叶）的无叶区存在较大的压力脉动。Parrondo-Gayo 等［5-6］测试了单吸离心泵的叶轮出口的压力脉动，发现压水室压力脉动水平主要受叶轮出口与压水室隔舌间隙和运行工况的影响，较小间隙和偏额定工况运行均会显著增大水泵的压力脉动。舒欣等［7］采用试验和数值模拟相结合的方法研究了自吸泵内部能量损失的特征，发现动静干涉效应会加剧叶轮内部和隔舌附近的损失。

泵内叶频压力脉动在隔舌区域最为显著［8-9］，且向周围传递脉动能量，势必对泵系统及泵房施加额外激振力。Hodkiewicz 等［10］针对双吸离心泵泵站开展了现场振动测试工作。结果表明，0.6倍额定流量下的水泵振动幅值可增大到额定流量下对应幅值的2倍，小流量工况是引起泵机组运行不稳定的主要原因。丁光等［11］研究了泵站机组和泵房振动特征，发现泵房振动受水力因素影响明显，压力脉动主频为叶频及其倍频。Yao 等［12］通过试验发现，泵在小流量运行时会出现低于转频的低频压力脉动，有时甚至会在管道系统中引起共振。Adamkowski等［13］发现泵轴固有频率与转动频率一致引起的共振导致泵轴严重断裂。

由于水泵启动过程遍历了所有小流量工况，可以推断水泵启动开阀过程与泵站系统运行稳定密切相关。傅里叶变换方法常被用于泵站振动信号的分析［14-15］，但对于大型双吸离心泵机组，水泵启动工况阀门从全闭到全开需要经历几十秒甚至几百秒的时间，压力脉动幅值具有显著的瞬态特征，在将压力脉动信号从时域变换到频域时，传统快速傅里叶变换无法体现信号的瞬变特性，需要采用时-频联合分析方法（时频分析）。时频分析常用的方法包括短时傅里叶变换方法（STFT）、连续小波变换方法（CWT）、Wigner-Ville变换方法（WVT）和希尔伯特黄变换（HHT）等。其中，连续小波变换分析方法基函数丰富，形式简单，应用起来更为灵活方便，适用于强瞬态特征信号的分析，在水力机械领域被广泛采用。

目前，对水泵压力脉动规律的认知主要来源于水泵模型测试台试验，且以稳态运行测试工况为主。为了研究泵站现场复杂运行条件下的压力脉动特性及其对泵站系统影响，本文针对某双吸离心泵供水泵站开展稳态工况和启动工况的现场试验，并对该泵站压力脉动与振动的测试结果进行分析讨论。

2 试验方案

2.1 试验对象试验对象为某双吸离心泵供水泵站，为干室型泵房。重点关注双吸离心泵泵体、上下游管路和水泵出水侧泵房楼板的振动特性，水泵机组布置如图1所示，水泵主要参数见表1。水泵进水管直径1.60 m，通过偏心异径管与水泵进口相连。水泵出口通过一扩散段和蝶阀相连，蝶阀直径和出水管管径均为1.40 m。规定水泵进出口主流流向为x轴，垂直方向为y轴，泵轴轴向为z轴。

图1 测试泵及泵房布置

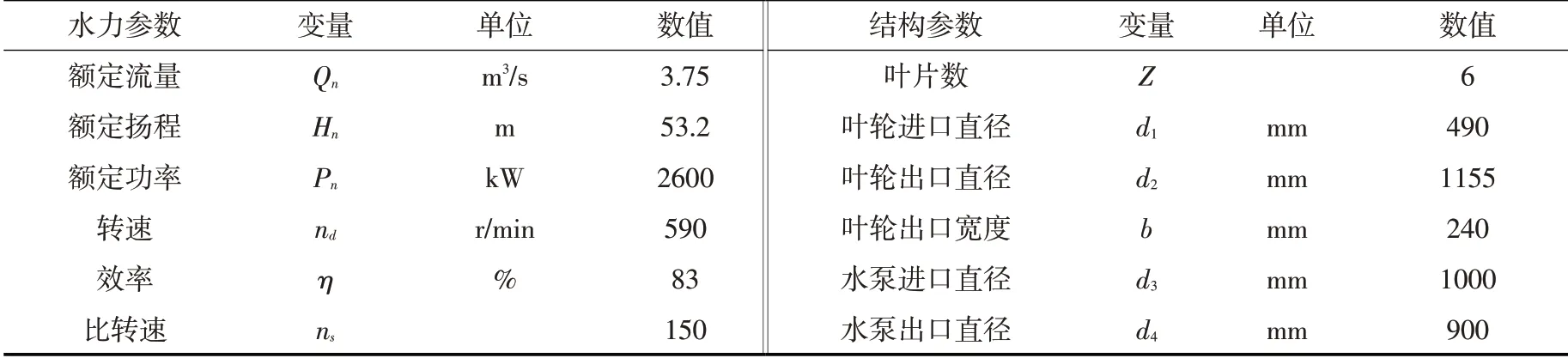
表1 测试水泵的特征参数

2.2 压力脉动与振动测量压力脉动和振动测点布置如图1所示。压力脉动传感器型号CGYL-201，量程分为两类，Ⅰ类量程-0.1～0.2 MPa，Ⅱ类量程0～1 MPa，动态响应频率为0-1500 Hz，精度为0.25%，使用DPI832标准压力计原位率定。压力脉动传感器测点共4处，分别位于水泵进口位置P1、压水室顶端位置P2、水泵出口位置P3以及出水阀后侧1 m处的出水管位置P4，其中P1处使用Ⅰ类压力脉动传感器，P2、P3、P4位置使用Ⅱ类压力脉动传感器。振动信号采集包括速度信号和加速度信号，振动速度信号采集使用振动速度传感器配合INV-9型信号调理积分放大器共同使用，测量范围从0.1 μm 到70 mm，频率响应在0.5～1000 Hz 之间。振动加速度传感器灵敏度系数为500 mV/g，输出电压为-5V～5 V，响应频率0～5000 Hz。速度信号侧重于衡量振动幅值总体水平，加速度信号侧重于测量水泵启动工况下结构的动态响应。振动速度信号测点共2处：（1）水泵基座处三个方向的振动速度Vpx、Vpy、Vpz；（2）出水管侧楼板处的垂向振动速度Vfy；振动加速度信号测点共2处：（1）出水管垂向振动Ap；（2）出水管上方楼板处的垂向振动Af。压力脉动与振动测量信号为同步采样，采用频率为3000 Hz，低通滤波截止频率为1000 Hz。

2.3 试验内容现场试验的内容包括稳态工况测试和启动工况测试。稳态工况是指水泵在某一固定流量下运行的工作状态。稳态工况试验包括水泵外特性试验、压力脉动试验和水泵基座以及楼板振动测量。启动工况是机组电机直启后泵后阀门从闭合到全开的整个过程。启动工况试验内容包括压力脉动试验和振动响应试验。

3 理论背景

3.1 参数定义对水泵流量、扬程和各测点压力脉动幅值做无量纲化处理，分别定义为流量系数Qc、扬程系数Hc和压力脉动系数CP，计算公式如下：

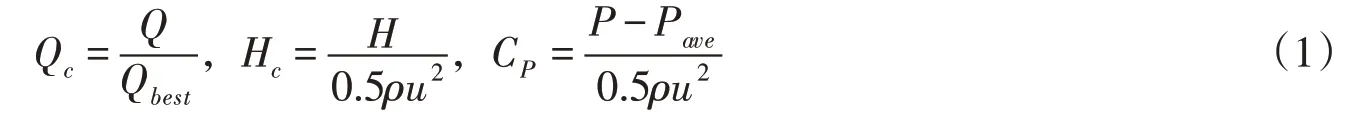
式中：Q为实际测得的流量，m3/s；H为实际测得的扬程，m；Qbest为泵最优效率对应的流量；ρ为介质密度，取1000 kg/m3；u为叶轮出口边速度，m/s；P为测点实际测得的压力；Pave为测点压力的平均值。

根据《GB/T 29531-2013 泵的振动测量与评价方法》，取振动速度信号的均方根值表征振动烈度ΔV，见下式：

式中：v为振动速度信号实测值，mm/s；N为被测信号的离散点数，N的采集时间满足《GB/T 29531-2013 泵的振动测量与评价方法》要求。

3.2 时频分析 对于稳态工况，泵站振动信号的分析应用离散傅里叶变换原理（DFT），见下式：

式中：f为离散的基频；T为总采样时间；X为基频f对应的信号幅值；xn为测得的第n个信号值；Δt为两次采样时间间隔。

对于启动过程泵站振动信号，采用连续小波变换［13］开展分析。连续小波变换可以同时在时域和频域观察信号，适用于动态过程信号的时频分析，其计算公式见下式：

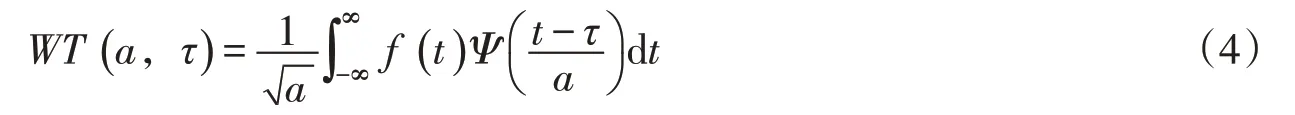
式中：小波变换有两个变量，尺度a和平移量τ，尺度a控制小波函数的伸缩，平移量τ控制小波函数的平移；是母小波函数。

连续小波变换中基函数的选取主要是考虑基函数对时间和频率分辨率的平衡。常见的基函数有Morse小波、Morlet小波和Bump小波等。Kumar等［16］和Pavesi等［17］等学者研究表明在离心泵压力脉动和振动信号分析中，相比其他基函数，Morlet小波具有更好的有限支撑性，在分析离心泵瞬态信号时具有很好的时间和频率分辨率，因此本文采用Morlet小波族，见下式：

3.3 相干性分析为了分析不同测点信号之间的相关程度，引入相干性分析方法。同样，根据水泵运行工况的不同，采用稳态和瞬态相干性分析方法。对于稳定运行工况，首先计算不同测点时序信号的自相关和互相关函数，然后，利用FFT 到相应的互相关（自相关）谱密度函数，最后计算相干性。单测点振动时序信号x（t）的自相关函数计算式为：

双测点振动时序信号x（t）和y（t）的互相关函数计算式为：

式（6）和式（7）得到的相关函数经快速傅里叶变换后得到自相关（互相关）谱密度函数，记为和，由此，两组信号x（t）和y（t）的相干性函数形式为：

对于水泵启动的瞬变工况，采用小波相干性分析方法，对式（6）和式（7）做连续小波变化得到自相关谱密度函数和互相关谱密度函数，见下式：

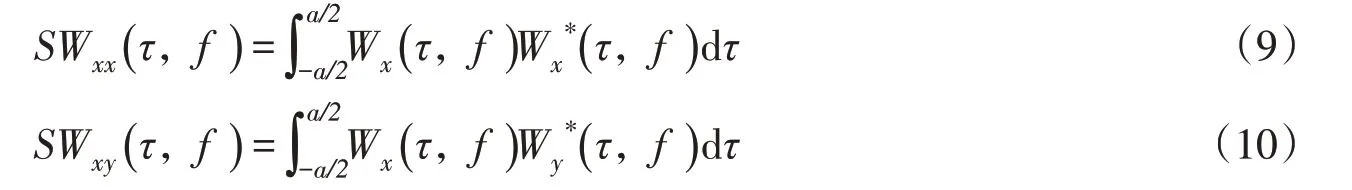
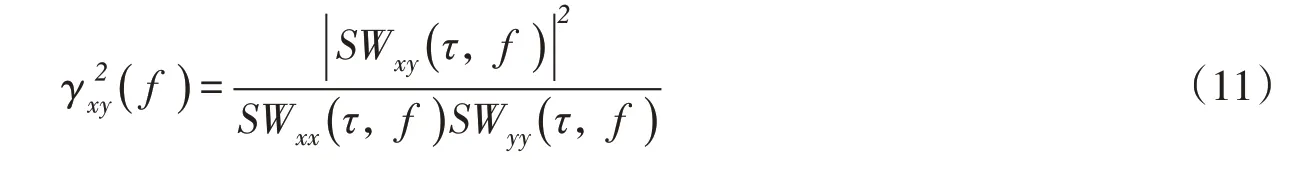
4 结果与讨论

4.1 稳态工况

4.1.1 压力脉动特性 前期已对水泵在0.36～1.21的流量范围内开展了11组稳态测试［18］，水泵外特性如图2所示。试验水泵在0.8～1.21的流量内运行效率均高于80%，最高效率为83%。

图2 双吸离心泵外特性

对最优效率工况点的压力脉动做频域分析，如图3所示。在最优效率点运行时，水泵4 个压力脉动测点主要频率成分为转频、叶频及其倍频。试验中测点P2的压力脉动最大，其主频为叶频，对应压力脉动系数值为0.016；次频为转频，仅为主频压力脉动系数值的21.3%；在1 倍叶频至10倍转频的频率区间内存在宽带频成分，其中心频率幅值与转频幅值相当，前期研究表明，宽带频中心频率会随流量发生移动［18-19］。测点P2的上游，水泵进口处P1的压力脉动主频为转频，对应的压力脉动系数CP值仅为P2处转频CP的9.1%。测点P2的下游，水泵出口测点P3压力脉动的主频为叶频，相较于测点P2，叶频幅值下降至34.2%；第二主频为转频，转频幅值为0.0033，相较于P3处转频幅值没有明显变化。出水阀后测点P4压力脉动的主要频率为转频、叶频以及其倍频，其中，转频幅值为P2测点对应值的72.0%，叶频幅值仅为P2测点对应值的6.5%。

图3 Qc=1时双吸离心泵系统的压力脉动分布

叶频压力脉动在整个泵系统中占主导，对其做进一步分析，如图4所示。在0.36～1.21流量范围内，各测点的叶频压力脉动系数值整体上呈现先降后升的趋势，其中P2的叶频压力脉动系数值最大，平均值为0.021；而水泵进口测点P1的叶频压力脉动系数值最小，仅为P2处的0.5%。测点P2的叶频压力脉动系数CP在流量0.67～1.18均低于0.02，和水泵效率高效区基本重合。0.75Q对应叶频压力脉动相对最低，原因在于：该频率除了动静干涉是主因外，还受宽带频影响，0.75Q以上流量，在叶频附近都存在低幅值的宽带频影响，如图3（b）所示，因此幅值相较0.75Q略高。但在流量1.21Q时，P2的叶频压力脉动系数值突增至0.050。在0.36～1.21的流量范围内，泵系统内部的叶频压力脉动系数值始终有P2>P3>P4>P1的关系，这意味着在泵系统中叶频压力脉动具有在上游衰减较快，在下游衰减较慢的特点。通过对相同泵型不同比转速的压力脉动实验调研［8，19-20］，认为该结果具有一定的普适性。其可能原因在于：叶频压力脉动产生于旋转叶轮与压水室的动静干涉，相对下游的传播路径，向上游传播时旋转叶轮的阻隔作用大幅度衰减了叶频压力脉动幅值。

图4 叶频压力脉动系数CP随流量变化

4.1.2 振动特性 图5 给出了水泵基座以及楼板处振动烈度随流量的变化曲线。在0.36～1.21 流量范围内，各测点的振动烈度整体上呈现先降后升的趋势，其中基座垂向ΔVpy最大，平均值为0.54；楼板垂向ΔVfy最小，平均值为0.08。在0.82～1.21 流量范围内，各方向的振动均较小，其中基座垂向ΔVpy均小于0.3 且平均值为0.24。该范围与高效区重合。当流量偏离高效区时，各测点振动烈度均有增加，其中基座垂向ΔVpy增幅明显，在流量为0.52 时达到最大值1.24 mm/s，是最高效率点的6.38倍。

图5 双吸离心泵基座、楼板的振动烈度ΔV

为了进一步分析影响振动的主要因素，对各工况下的振动信号做频率分析，如图6所示。各测点的频谱图中均存在明显的叶频振动速度，但其他频率成分差别较大。水泵基座径Vpx的主频是叶频，远大于其他频率所对应的振动速度，在最高效率点叶频振动速度是次频的3.89倍。基座垂向Vpy的叶频振动速度相对基座径向Vpx较低，但基座垂向Vpy在0.1倍转频处有一个低频宽带振动，这使得基座垂向ΔVpy高于基座径向ΔVpx；该低频宽带振动速度的幅值较大，在流量为0.52时达到最大值，单频振动速度是叶频振动速度的3.67倍，对应的频率为0.093倍转频。基座轴向Vpz在最优效率点的主频为叶频，在10倍转频处存在一宽带频；在偏离最优频率点后，基座轴向Vpz增大且出现大量宽带频，宽带频出现在1倍转频到12倍转频之间，成分复杂。楼板垂线Vfy的主要频率是叶频，且在6.8倍转频处存在一个幅值很大宽带频。该宽带频的振动速度在偏离高效区时明显增大，在流量为0.36时，宽带频单频最高幅值是叶频振动速度的2.23倍。值得注意的是：基座轴向和径向两个方向振动都在1.2Q出现下降，从频谱表现来看，振动幅值下降主要体现在叶频幅值下降上。由此推测，这一现象与大流量工况水泵内部各向异性大尺度旋涡流动对动静干涉的影响有关，但其背后机理还需要借助计算流体动力学（CFD）和流固耦合（FSI）数值计算，进行更为深入的研究。

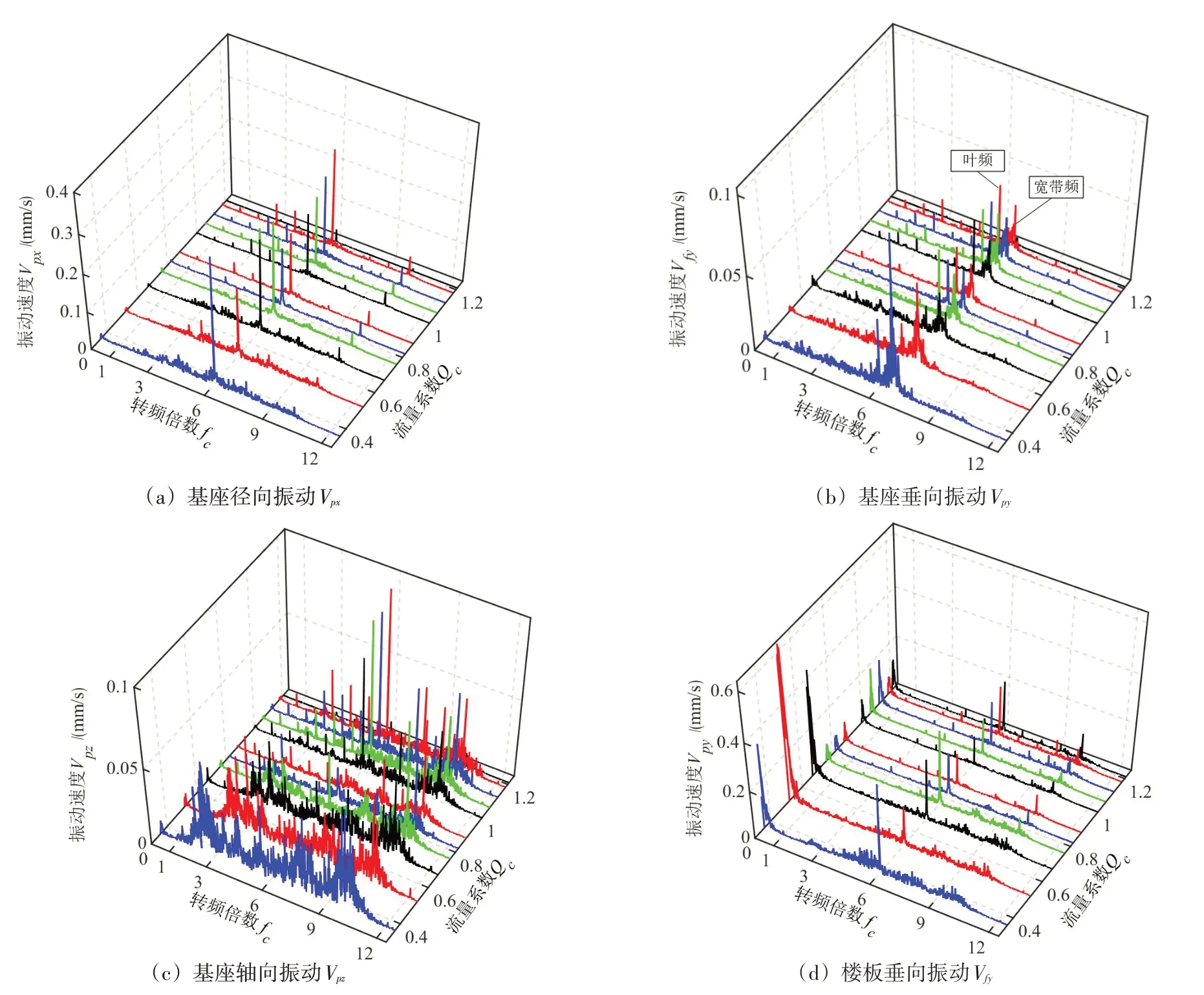
图6 双吸离心泵系统振动速度的频域

4.1.3 压力脉动与振动的稳态相干性分析 分别对水泵压水室压力脉动P2与基座垂向Vpy、出水阀门后压力脉动P4与楼板垂向Vfy做相干性分析，如图7所示。图7（a）中，高效区运行时，压力脉动P2与基座垂向Vpy的1倍转频、3倍转频、4倍转频，以及1倍叶频处呈现较高的相干性，而在小于1倍转频的低频区域的相干性较小；在偏离高效区的小流量工况区域，P2与Vpy的相干性主要体现在叶频。压力脉动P4与楼板振动Vfy的相干性和P2与Vpy的相关性类似，主要出现在1倍转频和6倍转频之间。需要注意的是两者虽然在0～0.2倍转频的相干性很高，但该段频率对应的压力脉动和振动速度幅值均较小，而6.8倍转频处楼板垂向Vfy与压力脉动P4没有表现出很强的相关性。

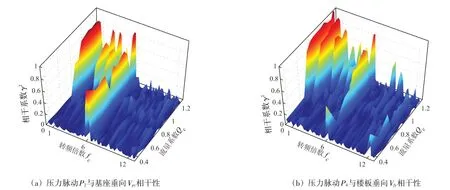
图7 稳态工况中压力脉动与振动的相干性分析

在双吸离心泵系统稳定运行时，压水室顶部P2的叶频压力脉动远大于其他测点；在试验测试范围内（Qc=0.36～1.21）叶频压力脉动在上游的衰减较快，在水泵进口处已基本消失；相对于P2，下游P4处叶频压力脉动时衰减93.5%。双吸离心泵系统在高效区运行时，水泵基座和楼板的振动烈度较弱。水泵基座垂向的振动最剧烈，且在小流量工况时（Qc=0.36～0.67）出现了强烈的低频振动。双吸离心泵系统稳定运行时，系统内部的压力脉动与振动的相干性仍主要表现在水泵高效区的转频、叶频以及其倍频。

4.2 启动工况

4.2.1 压力脉动特性 图8是随着阀门开启，叶频压力脉动系数逐渐变化的曲线。在双吸离心泵系统启动工况中，水泵进口P1、水泵出口P3、出水阀后P4的叶频压力脉动系数的平均幅值和稳态工况相当，且随着阀门开度增大没有明显变化，如图8（a）所示。压水室测点P2的叶频压力脉动系数变化明显，如图8（b）所示。P2的叶频压力脉动系数值在开阀初期最大，试验中最高达到0.28。在阀门开度a=0～40%范围内，随着阀门开度逐渐增大，P2的叶频压力脉动系数值快速下降，称这一范围为压力脉动下降阶段；在阀门开度a=40～100%范围内，P2的叶频压力脉动系数值趋于平稳，称这一范围为压力脉动平稳阶段，在这一阶段内的P2的叶频压力脉动系数平均值为0.015。

4.2.2 振动特性 图9为水泵基座三个方向振动速度的频域分析图。基座径向Vpx的主要频率成分比较复杂。在压力脉动下降阶段，Vpx的主要频率成分是集中在2 倍转频和9 倍转频附近的两个宽带频，幅值随着阀门开度的增大逐渐下降；当阀门开度a达到40%，也就是在压力脉动平稳阶段内，2 倍转频附近的振动速度基本消失，只剩下6 倍转频到9 倍转频的宽带频振动。基座垂向Vpy的主要频率是叶频的宽带频。在压力脉动下降阶段，基座垂向Vpy的叶频附近存在宽带频范围在2 倍转频到12 倍转频之间，但这个区间随着阀门开度增大而缩小，在阀门开度达到30%之后，叶频振动速度幅值也后逐渐减小并趋于稳定。基座轴向Vpz和基座垂向Vpy趋势相似，但幅值较小，Vpz的单频最大值为0.32 mm/s，仅为基座轴向Vpz单频最大值的46.4%。

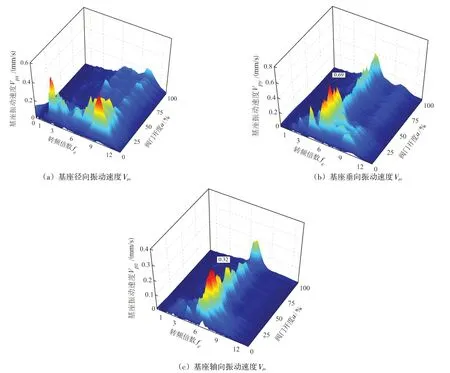
图9 阀门启动时水泵基座振动速度频域

出水管的振动将直接影响楼板振动，二者振动加速度A随阀门开启时的振动变化图10所示。启动过程中出水管振动加速度Ap主要频率是一个宽带频，该宽带频范围在4倍转频和7倍转频之间，宽带频在5.28倍转频处取得最大幅值0.593 mm/s2，推测该频率可能是出水管的固有频率。出水管振动加速度Ap的在刚开阀时幅值较小；当阀门开度达到3.6%时，Ap突增至0.342 mm/s2。楼板振动加速度Af的主要频率是叶频附近的宽带频。启动过程中出水管振动Ap和楼板振动Af的变化趋势一致，当阀门开度达到3.6%时，Af突增至0.010 mm/s2，并在压力脉动下降阶段幅值逐渐降低，在压力脉动平稳阶段趋于平稳。

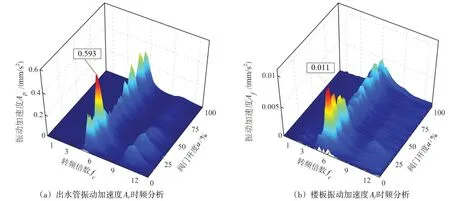
图10 阀门启动时的出水管和楼板振动加速度分析

4.2.3 压力脉动与振动的瞬态相干性分析 图11为水泵压水室内压力脉动P2和基座垂向振动速度Vpy的相关性分析结果。在机组启动2.1 s时（阀门开度a为6%），P2和Vpy首先在叶频处出现了明显的相干关系，但随着时间变化，两者的相位角相差不断改变且没有明显规律，在17 s（阀门开度a为60%）时两者不再表现出明显的相干性；在开阀10 s（阀门开度a为32%）时，P2和Vpy在转频处表现出明显的相干关系（相干系数γ2>0.7），且两者的相位角比较稳定。同时对出水管的压力脉动P4和楼板垂向振动速度Afy的相干性分析，如图12所示，两者在叶频和转频上间歇地表现出相对较强的相干性，可以推测，当楼板固有频率与叶频转频接近时，有可能诱发共振。

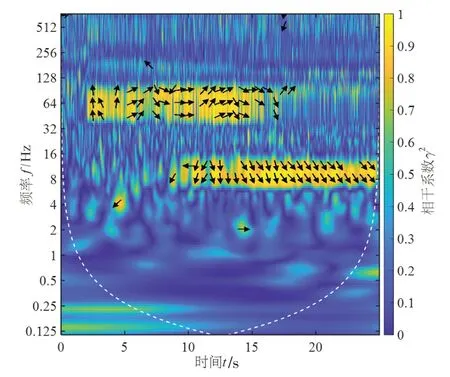
图11 压力脉动P2和基座垂向振动Vpy的相干性

图12 压力脉动P4和楼板垂向振动Afy的相干性

在启动工况中，双吸离心泵压水室顶P2的叶频压力脉动系数远大于其他位置，且在压力脉动下降阶段快速下降，并在压力脉动平稳阶段趋于稳定值。水泵基座、出水管和楼板振动的主要频率成分是叶频的宽带频。水泵基座振动速度的变化趋势和P2的叶频压力脉动系数变化趋势一致；出水管和楼板振动在阀门开度为3.6%时突然加剧，在达到峰值后逐渐下降并趋于平稳。压力脉动P2和基座垂向Vpy先后在叶频和转频处表现出明显的相干性，出水阀后P4和楼板垂向Afy在叶频和转频处间歇性出现较强相干性。

5 结论

为了揭示泵站压力脉动与振动特性及其相互影响，对某双吸离心泵泵站开展了外特性、压力脉动和振动现场试验。采用经典频谱分析、连续小波变换和相干性分析等方法，分析了双吸离心泵系统压力脉动和振动的时空分布特征，并分析了两者的相互关系。主要结论如下所示：（1）稳态工况下压力脉动与振动在转频、叶频及其倍频处表现出相关性。稳态工况下压水室顶P2的叶频压力脉动系数大于其他测点；水泵压水室压力脉动P2与基座垂向Vpy、出水阀门后压力脉动P4与楼板垂向Vfy的相干性主要表现在转频、叶频及其倍频成分上。（2）启动工况中双吸离心泵系统的压力脉动和振动的变化趋势基本一致。在压力脉动下降阶段（阀门开度a=0%～40%），P2的叶频压力脉动系数快速下降，并在压力脉动稳定阶段（阀门开度a=40%～100%）趋于稳定；水泵基座、出水管和楼板振动的主要频率成分是叶频的宽带频；出水管和楼板的振动有滞后现象，在阀门开度3.6%时达到峰值。（3）启动工况中双吸离心泵系统的压力脉动和基座振动的相干性明显，与楼板的振动出现间歇性相干。水泵压水室压力脉动P2和基座垂向振动Vpy先后当阀门开度a为6%和32%时，在叶频和转频处表现出明显的相干性，而出水阀后的压力脉动和楼板垂向振动在整个启动阶段没有表现出连续的相干性。

总体而言，水泵叶频压力脉动是干室型双吸离心泵泵房的最主要水力激振源，该类型泵房在设计时，需要格外关注叶频压力脉动作用下出水侧楼板等泵房结构的动力学响应问题。