基于贝叶斯模式平均与区间二型模糊集的分区灌溉方法
邵东国,邹亮峰,顾文权,农翕智,王 鹤,王 柏
(1.武汉大学水资源与水电工程科学国家重点实验室,湖北武汉 430072;2.黑龙江省水利科学研究院,黑龙江哈尔滨 150080)
1 研究背景
松嫩平原是我国重要的粮食产区,受气候变化与粮食市场的影响,松嫩平原水稻种植面积不断扩大[1-2],水田灌溉用水占农业用水80%以上[3],局部地区出现地下水超采现象,对当地河湖湿地生态系统构成严重威胁[4]。因此,合理优化水稻灌溉制度,推行节水控采,缓解地下水超采现象,对保护当地粮食生产与河湖湿地生态系统稳定具有重要意义。
作物灌水量与地下水埋深之间存在一定相关性[5-6]。在干湿交替稻田中,地下水通过毛管上升成为可供水稻根系吸收利用的土壤水,从而影响根区土壤水分分布[7-9]。地下水埋深的变化将改变稻田地表水-土壤水-地下水之间的转化运动规律,进而影响稻田渗漏与作物需水量[10]。现有水稻灌溉制度优化研究,大多基于作物耗水与田面水层等试验监测数据,通过多目标遗传算法与水分生产函数、水量平衡等模型耦合,忽略了稻田地下水埋深对灌水量的影响[11-14]。实际上,随着东北等地大规模集约化水稻生产的推进和降雨、地下水开采等非均匀分布影响,水稻种植区存在明显的地下水埋深时空变化[15-17]。因此,需要根据水稻种植区不同地下水埋深对稻田渗漏与水稻作物需水等的影响差异,通过不同区域地下水埋深差异分区来进一步优化水稻灌溉制度,最大限度地提高毛管水的利用率,减少稻田深层渗漏量,实现大规模集约化水稻种植区域的高效节水灌溉。
灌溉制度优化研究中,产量模拟的精度决定了优化结果的可靠性[18]。AquaCrop 作物模型内置地下水模块[19],能模拟动态地下水埋深条件,所需参数少且便于多情景模拟,但产量模拟精度较差[20-22]。作物水分生产函数模型根据当地田间试验数据确定,在产量模拟方面更具针对性,模拟精度更高,但缺少对田间地下水影响的考虑[23]。因此,需要深入研究地下水埋深动态变化条件下,提高作物产量模拟精度的有效方法。
考虑到现有灌溉管理决策常凭经验或用水计划,忽略了农业生产中气候、灌溉等农业活动的随机性,以及决策者的风险偏好与判断模糊性,导致灌溉制度优化结果过于理想化,而经验性灌溉制度又常发生灌溉退水现象,造成灌溉水资源浪费[24-26]。如何综合考虑农业集约化生产过程中灌溉决策的不确定性,结合决策者主观风险倾向进行灌溉制度优化决策,是提高灌溉制度优化结果实用性与有效性的重要途径。
本文以松嫩平原北部和平灌区水稻种植区2017-2019年降雨-地下水-产量监测试验为基础,通过分析地下水埋深变化规律,基于空间拓扑关系聚类分析与空间叠加分析确定研究区地下水埋深的分区界限;设定AquaCrop 模型[19,22]中不同区域地下水埋深模块,运用AquaCrop 和Jensen 模型[23]对平、枯水年各区不同灌溉情景进行产量模拟,并用贝叶斯模式平均方法(BMA)[27-29]融合两个模型的产量模拟系列,基于区间二型模糊集理论[30-32]从节水、增产与地下水稳定三个属性对灌溉情景进行模糊综合评价,结合决策者风险偏好,采用有序加权算术平均算子(OWA)集结各典型年不同分区所有灌溉情景评价值,实现灌溉制度模糊综合优化决策,以期为水稻规模化种植区提供基于地下水埋深动态的分区节水控采新方法。
2 灌溉区域地下水埋深动态分区
2.1 地下水动态监测试验及分区方法
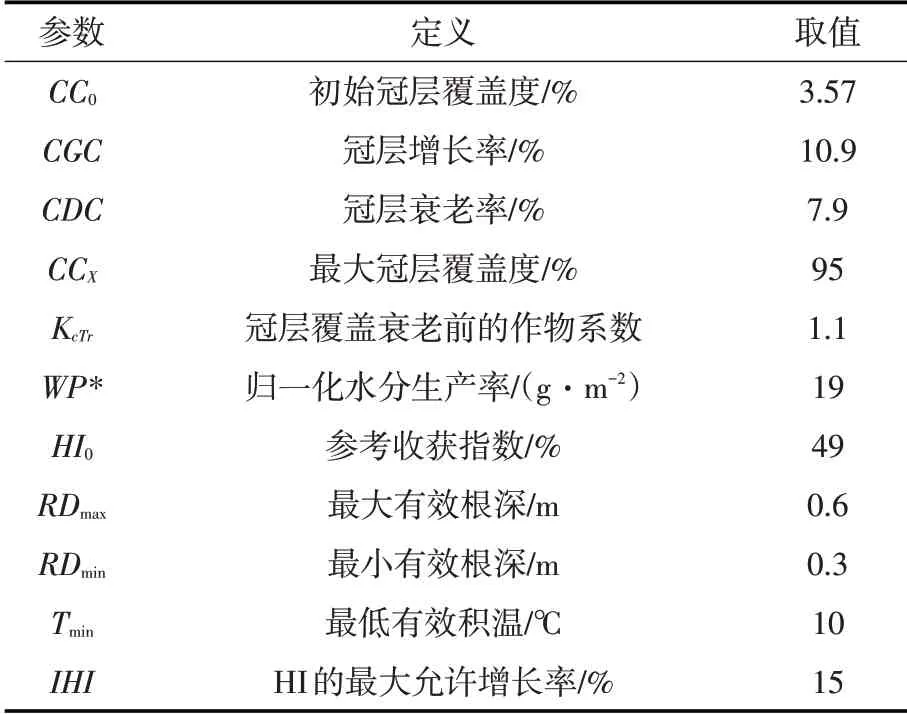
2.1.1 地下水埋深监测试验 试验于2017—2019年在松嫩平原北部(黑龙江省庆安县)和平灌区水稻灌溉试验站开展,该区域为平原区,地势平坦,属于北温带大陆性季风气候,多年平均降雨量558 mm,多年平均蒸发量764.5 mm,多年平均气温2.5 ℃,年内气温变幅较大,夏季极端最高气温36.7 ℃,冬季极端最低气温-44.9 ℃,无霜期128 d。试验区位于寒地黑土核心区,土壤种类为白浆型水稻土,土壤容重为1.02 g/cm3,土壤基本理化性质为:pH值6.40,全氮15.10 g/kg,全磷15.21 g/kg,全钾20.09 g/kg,有机质41.5 g/kg。区域内设有7 眼地下水观测井,根据试验区地形条件,均匀分布在主要排水口附近,在生育期内采用地下水监测系统逐日观测地下水埋深(Groundwater depth,GD),具体分布如图1所示。

图1 地下水监测井分布
2.1.2 分区方法 采用线性函数归一化方法,对生育期内地下水埋深监测数据进行归一化处理。基于K-Means聚类算法对归一化后的埋深数据进行聚类分析,确定灌溉区域根据地下水埋深分区的节点。K-Means 聚类算法的思路为,使样本空间所有的非中心点到各自所属簇的中心点的距离的平方和最小,目标函数F为:
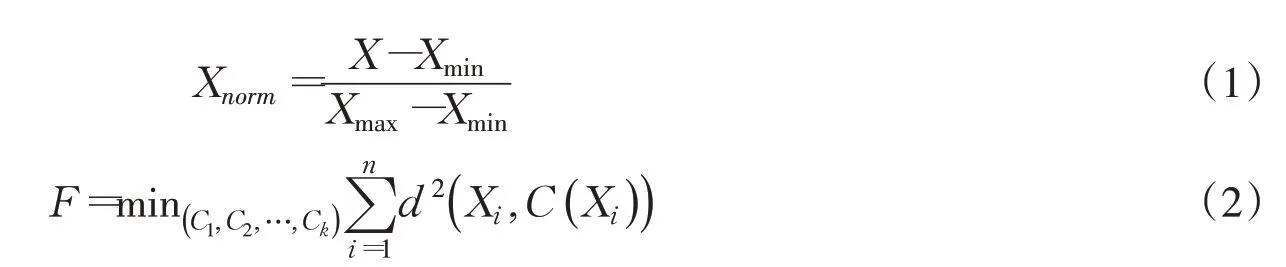
式中:Xnorm为归一化后数据;X为原始数据;Xmax、Xmin分别为原始数据集的最大值与最小值;C1、C2、…、Ck分别是k个簇的中心点;C(Xi)为Xi点所属的簇的中心点;d2(Xi,C(Xi))为求两点的的距离平方。
根据聚类分析结果,基于ArcGIS平台采用Kriging插值方法进行多次插值,通过分析地理实体的拓扑关系,对插值结果进行空间叠加分析,最终实现区域分区。
2.2 地下水动态分析及分区结果
2.2.1 地下水埋深动态分析 根据2017、2018年地下水监测数据,计算生育期平均地下水埋深(Av⁃erage groundwater depth,AGD),结果见图2。从图2 可以看出,2017年AGD在1.25~2.12 m 之间变化,变幅为0.87 m;2018年AGD在0.65~2.03 m之间变化,变幅为1.38 m;2018年为特丰水年,降雨量较大,因此地下水埋深波动更加剧烈,2018年AGD变幅相比2017年增加了58.6%。
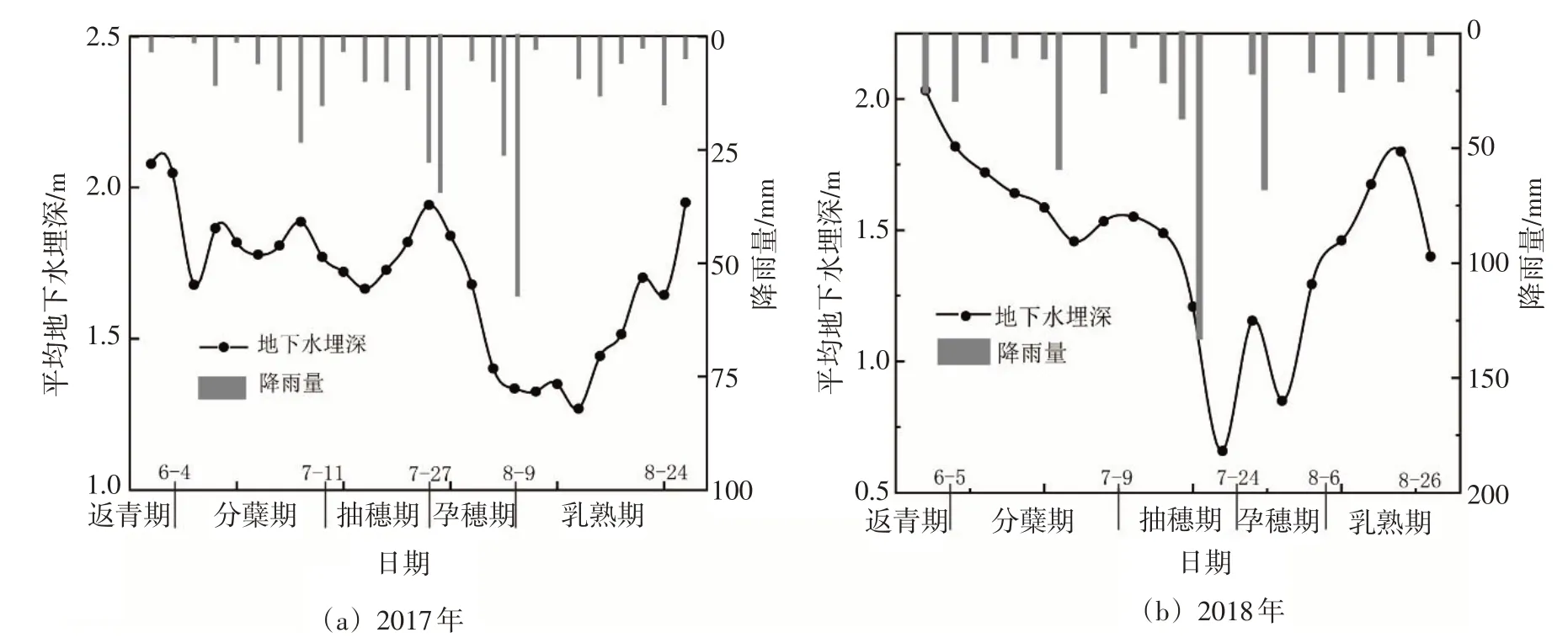
图2 生育期区域平均地下水埋深与降雨量关系
受降雨、灌溉等因素影响,水稻不同生育期内地下水埋深不同。分蘖期以灌溉为主,降雨量少,GD在1.55~2.03 m 之间;孕穗期、抽穗期降雨丰富且集中,因此GD逐渐减小,2017、2018年GD分别为1.32 ~ 1.76 m 和0.65 ~ 1.49 m;乳熟期降雨、灌溉减少,使得区域GD增加,GD在1.52~1.85 m之间。
2.2.2 地下水埋深分区结果 根据2017年、2018年监测数据对地下水埋深进行频数分布统计,其结果如图3所示,GD近似满足正态分布。调用R语言中kmeans()函数,设置类别数k=2,分别对2017年、2018年GD数据(一维数据)进行聚类分析,结果如表1所示,将GD监测数据分为两簇后,簇1 以1.8 m 左右为数据中心,簇2 以1.48 ~1.17 m为数据中心。
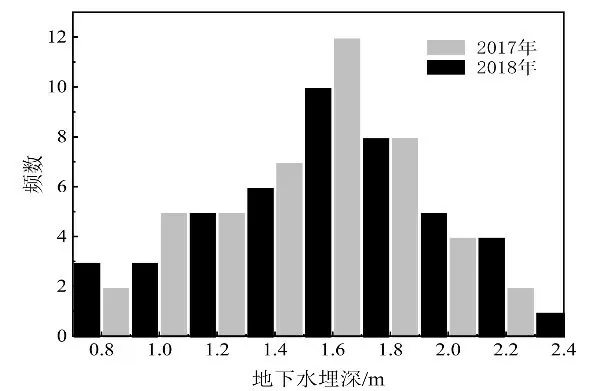
图3 地下水埋深监测数据频数分布直方图

表1 地下水埋深数据聚类分析后各簇数据质心结果
土壤水-地下水垂向运动规律研究表明,地下水埋深增加将导致稻田渗漏量增大,作物对地下水的利用率降低[33]。GD>2.8 m后,垂向运动以深层渗漏为主,地下水无法补给作物需水[9];GD<0.7 m 时,地下水蒸发量较大,易发生土壤盐渍化,阻碍作物生长及其根系发育[11];埋深1.5 m介于两簇质心之间,与聚类分析结果相契合,以此为分区界限可以兼顾深层渗漏与毛管上升对稻田灌水量的影响。基于GD聚类分析结果,结合土壤水-地下水垂向运动规律,最终确定分区灌溉的地下水埋深分区界限为1.5 m。
以埋深1.5 m为界限,结合2017、2018年水稻不同生育期区域地下水埋深的多次Kriging插值结果,对研究区进行初步分区。根据地理实体的拓扑关系,采用空间叠加分析方法对初步分区结果进行相交分析,最终分区结果如图4所示(Ⅰ区表示GD≤1.5 m的区域,Ⅱ区为GD>1.5 m的区域),为确定不同地下水埋深区域的水稻最优灌溉模式、保证地下水可持续利用奠定了基础。

图4 结合聚类分析、多次Kriging插值与相交分析对灌域地下水埋深分区结果
3 基于贝叶斯模式平均方法的分区产量模拟模型
3.1 产量模拟模型为深入揭示灌区地下水埋深动态对水稻产量的影响,利用AquaCrop模型地下水模块[19]模拟不同地下水埋深分区的作物灌水与产量关系,但产量模拟精度次于水分生产函数模型。因此,为提高产量模拟精度,以AquaCrop模型中各区地下水动态埋深为控制条件,将该模型模拟所得水稻蒸发量结果作为Jensen 水分生产函数模型[23]的输入,得到不同地下水埋深区域的产量模拟值,通过贝叶斯模式平均(BMA)方法[29]将AquaCrop与Jensen模型产量模拟结果融合,得到精度更高的整合产量系列。
3.1.1 AquaCrop作物模型 AquaCrop模型是基于水分驱动的日尺度作物生长模拟模型,主要根据实际蒸腾量与归一化水分生产率计算生物量,利用收获指数和生物量的乘积确定最终产量。计算公式为:

式中:B为生物量,t/hm2;Tr为实际蒸腾量,mm;WP*为归一化水分生产率;HI为收获指数,%;Y为产量,t/hm2。
模型运行需要输入:气象参数、作物参数、田间管理参数、土壤参数[19]。AquaCrop模型地下水模块中设定不同地下水埋深调节土壤水分胁迫程度。
3.1.2 水分生产函数模型 选取Jensen水分生产函数模型描述水稻不同生育期水分-产量关系,可表示为:

式中:Ya、Ym分别为作物全生育期内的实际产量和最大产量,kg/hm2;ETa、ETm分别为全生育期作物实际腾发量和最大腾发量,mm;λi为i生育阶段缺水对作物产量影响的敏感性指数,即水分敏感指数;n为生育阶段数。
将其转化为多元线性方程,采用多元线性回归分析方法求解各系数,得到适合研究区的Jensen模型[24]为:
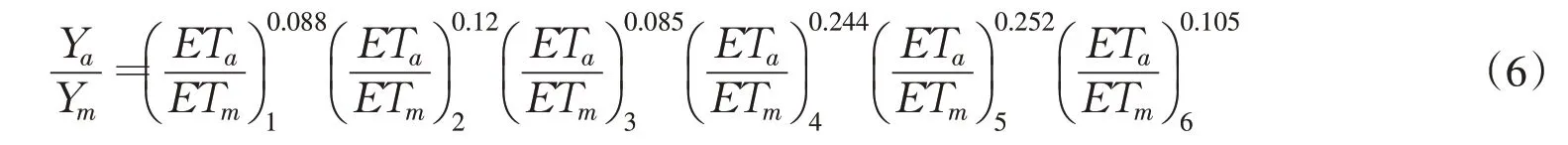
式中下标1、2、3、4、5、6分别代表分蘖前中后期、拔节期、抽穗期与乳熟期。
3.1.3 贝叶斯模式平均(BMA)方法 BMA方法[28]是一种集合不同模型模拟值,得到更可靠的综合模拟值的统计后处理方法。假设S为产量模拟量,R=[X,Y]为输入数据(其中X代表各模型模拟产量,Y代表实测产量),是K个模型模拟的集合,基于贝叶斯全概率公式可得模拟量S的概率密度函数为:
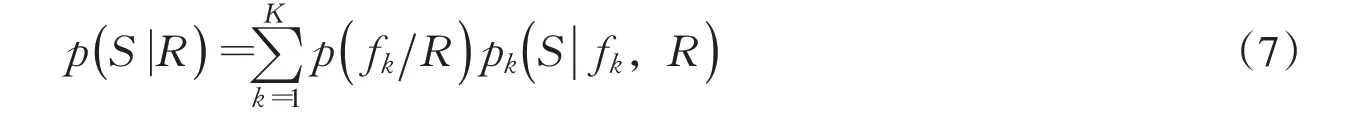
BMA方法采用后验概率作为权重,对各模型模拟值进行加权平均,最终输出综合模拟结果,精度较高的模型权重值更大。若单个模型模拟值与实测值均符合正态分布,可用BMA方法的校正公式:
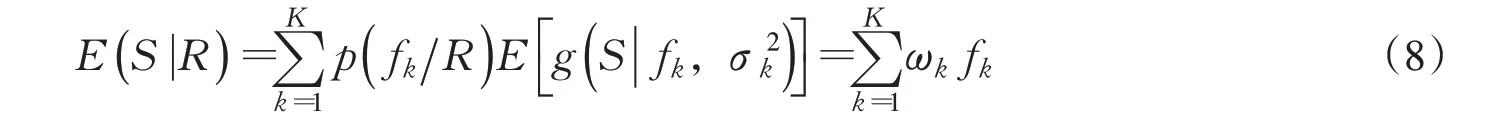
3.2 灌溉情景设定根据庆安气象站历史数据,采用优化适线法选取Pearson-Ⅲ型曲线进行拟合。选取1992年(P=50%)为典型平水年,2007年(P=85%)为典型枯水年,各典型年份生育期累计降雨量分别为426和274 mm。
根据灌区地下水埋深分区结果(Ⅰ区、Ⅱ区GD数值)设定AquaCrop地下水模块动态GD情景。通过增加或减少灌水次数、加大或降低灌溉定额的方式,基于解空间动态缩减策略[34]共组合生成576种灌溉模拟情景,组合方式见表2。

表2 灌溉情景设定
采用AquaCrop 模型对各典型年不同分区所有灌溉情景进行蒸发量-产量模拟,同时基于模拟所得蒸发量计算各灌溉情景下Jensen模型产量值。
4 基于区间二型模糊集的灌溉制度风险决策模型
4.1 基于IT2FS 的模糊决策模型在灌溉制度优选中,受管理者主观因素影响,常存在一定模糊性。为提高优选结果的合理性,本文基于区间二型模糊集(IT2FS)[32]建立了灌溉制度模糊决策模型,主要采用效用函数(U(A))度量IT2FS的优劣性,以区间二型模糊集熵(E(A))度量IT2FS自身的不确定性[31]。同时引入风险偏好因子(θ)刻画不同决策者的风险态度,各属性权重由E(A)和θ共同确定。采用有序加权算术平均算子(OWA)集结各方案属性权重与效用函数得到综合效用值。
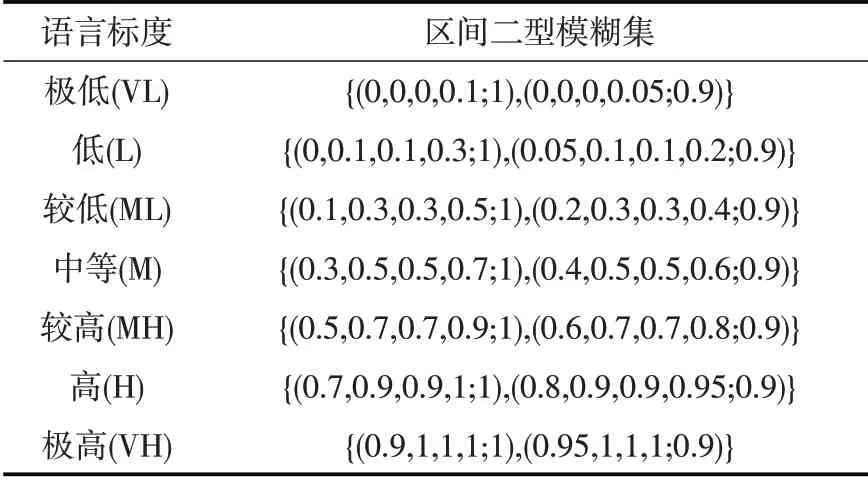
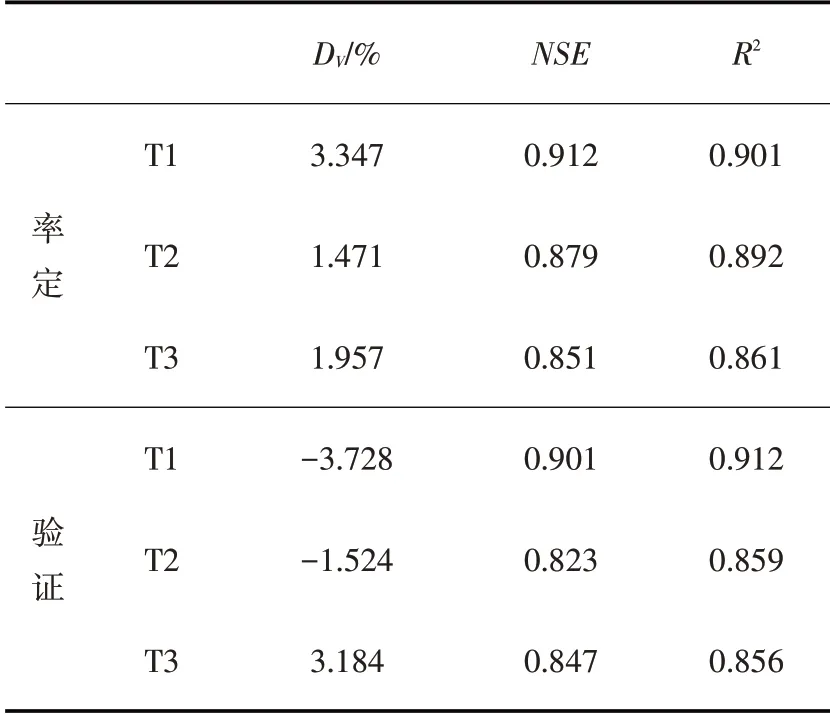
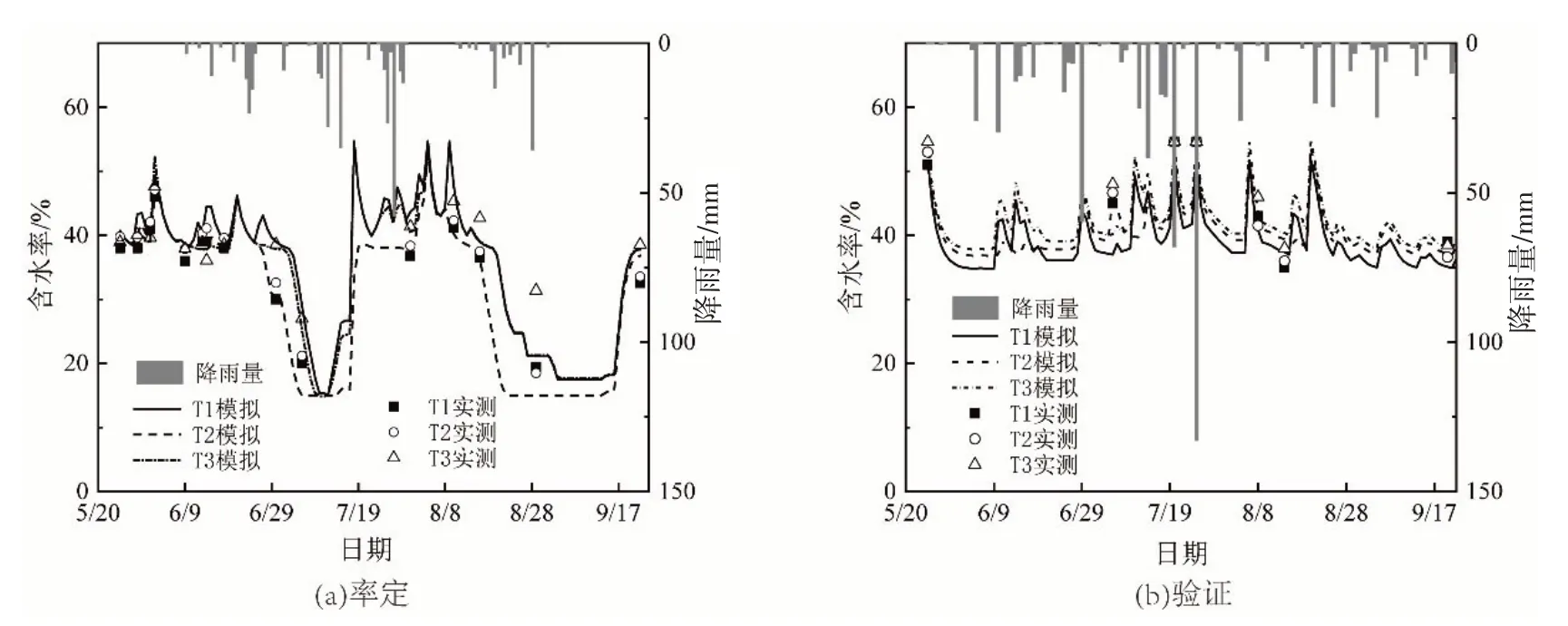
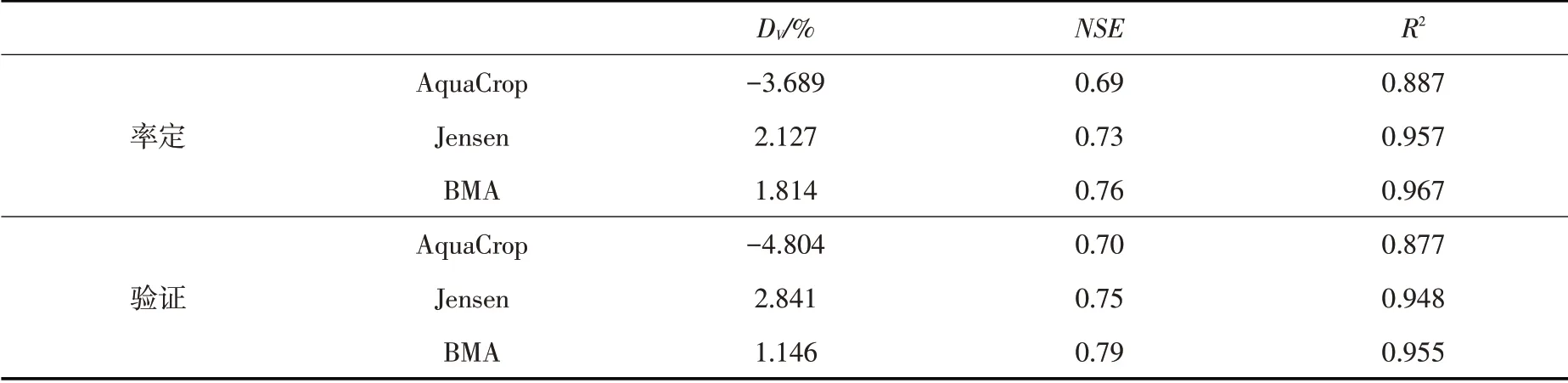
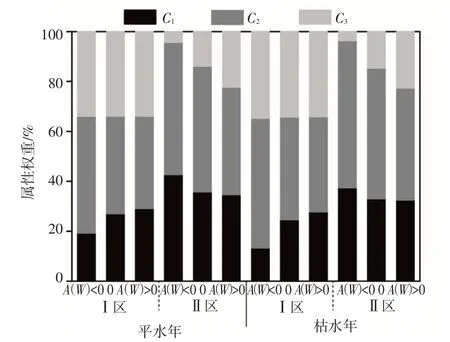
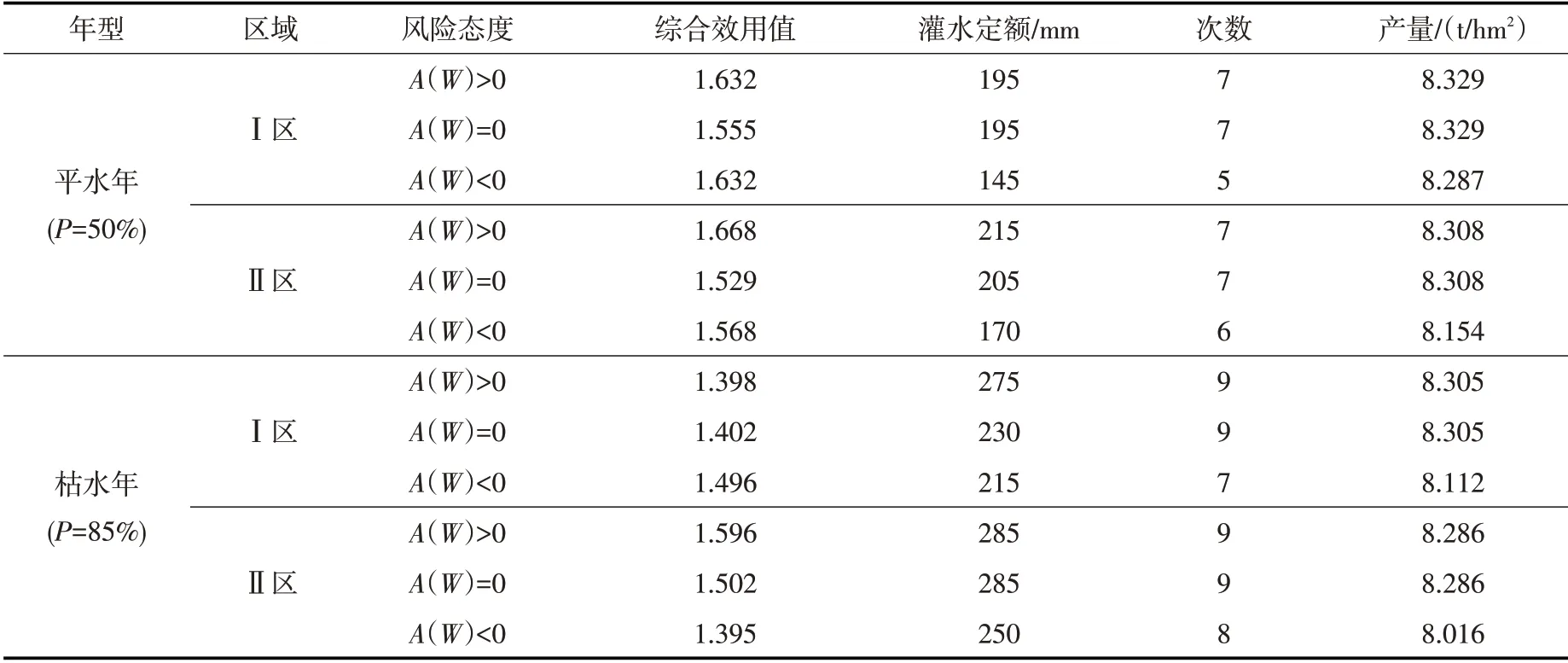
对于有n个方案集xi(0 (1)对各方案的所有属性进行模糊评价,得到原始决策矩阵A=(aij)n×m(aij均是IT2FS,表示决策者对某方案的评价结果)对其进行规范化得到规范化决策矩阵D(dij)n×m。 (2)计算D矩阵的效用函数U(dij)n×m和区间二型模糊集熵E(dij)n×m。 (3)计算不同决策风险偏好时各属性权重。 (4)根据属性权重与效用函数,利用有序加权平均算子集结不同风险偏好下各方案综合效用值U: 式中:bj为U(dij)第j行元素中第j大的元素;ωj为第j个属性的权重。 4.2 决策模型属性与标准设定根据产量模拟结果,从节水效益(C1)、增产效果(C2)和地下水埋深的稳定性(C3)三个属性对各典型年不同地下水埋深区域所有灌溉情景进行评估。评估结果用语言进行标度,各语言标度对应的区间二型模糊集如表3所示。 表3 语言标度及其对应的区间二型模糊集 5.1 产量模拟模型率定验证结果根据2017、2018年田间实验数据[23,33]对AquaCrop模型、BMA法参数进行率定、求解。选取体积差DV[35-36]、纳什系数NSE和决定系数R2评价模型模拟精度。 5.1.1 AquaCrop模型率定验证结果 选取土壤含水率指标检验AquaCrop模型适用性,以2017年控灌(T1)、浅晒浅灌(T2)、淹灌(T3)处理数据率定模型,调整作物参数,率定后部分参数见表4。以2018年为验证期,模拟得到土壤含水率与实测数据比较见如图5,精度评价结果见表5。对比土壤含水率实测值和模拟值,实测点均落在模拟含水率曲线附近,模拟值正负体积差DV不超过3.8%,R2与NSE均在0.8以上,说明土壤含水率模拟值与实测值之间一致性强,AquaCrop模型适用性高。 表4 率定后的模型输入参数 表5 含水率模拟评价指标 图5 土壤含水率实测值与模拟值对比 5.1.2 BMA 参数估计与产量模拟精度结果 基于2017、2018年实测产量系列[23]、AquaCrop[19]与Jensen模型[23]模拟产量系列,采用期望最大化(EM)[27]算法并结合R语言BMS包求解BMA方法中各模型所占权重。结果显示,AquaCrop模型所占权重为0.402,Jensen模型权重为0.598,表明Jensen模型产量模拟精度更高。 表6为贝叶斯模式平均(BMA)方法[29]及其2个模型产量模拟精度评价结果。从表6可知,AquaC⁃rop模型高估产量(DV<0),Jensen模型低估产量(DV>0),采用BMA方法可以调和两个产量模拟系列;BMA方法的确定性系数(R2)均在95%以上,大于任一单个模型的R2;BMA方法的纳什效率系数NSE最大,表明经过BMA方法融合后的产量模拟精度比单一模型的模拟精度高。 表6 BMA方法与单一模型产量模拟精度评价结果 2017、2018年实测产量与模拟产量对比图6。从图6可以发现,BAM方法产量模拟效果最优,产量的相关系数超过0.95,AquaCrop 模型效果最差。因此,在动态地下水埋深条件下,采用BMA方法[29]融合AquaCrop、Jensen模型的模拟产量能够提高和平灌区产量模拟精度。 图6 模拟产量与实测产量对比 5.2 分区灌溉模拟结果各典型年不同地下水埋深区域所有灌溉情景产量模拟结果见图7(Ⅰ区表示GD≤1.5 m 的区域,Ⅱ区表示GD>1.5 m 的区域)。采用Mann-Kendall趋势检验法,对各年型不同区域所有灌溉情景的产量进行趋势检验,结果见表7。结果显示,不同年型各区域产量趋势检验值均小于-2.58(显著性水平0.01),随着灌水量增加,产量总体呈显著下降趋势,但枯水年产量变化趋势与总体变化趋势存在差异。 图7 Ⅰ区、Ⅱ区不同灌溉情景产量-灌水量关系 表7 产量Mann-Kendall趋势检验值 筛选相同灌水量下各典型年不同区域产量最大的灌溉情景,拟合产量-灌水量关系曲线,结果如图8、表8所示。结果表明,水稻产量-灌水量响应规律呈非线性关系。灌水量较小时,土壤含水率较低,作物受到一定程度干旱胁迫,阻碍干物质累积与产量形成,此时增加灌水能够降低水分胁迫程度,促进产量形成;枯水年水分胁迫更严重,产量形成受到抑制,增加灌水能显著降低水分胁迫对产量形成的抑制作用。灌水量较大时,土壤常处于饱和状态,土壤含氧量和透气性低,导致水稻根系发育受阻,进而影响产量形成;灌水量越大,越容易产生深层渗漏,造成无效灌水。因此,随灌水量增加,水分胁迫逐渐消除,产量为增长趋势,而后影响根系呼吸进而降低产量,但产量整体仍然呈现随着灌水量增加而降低的趋势。 表8 各年型不同区域产量-灌水量拟合曲线方程 图8 产量与灌水量拟合曲线 随着灌水量增加,Ⅰ区最早出现产量降低现象,Ⅱ区较晚出现。原因是地下水埋深小时,地下水可通过毛管水上升供给水稻需水,此时土壤水分垂向运动为毛管水上升过程,增加灌水量会更早影响根系呼吸作用,最终导致产量降低;埋深较大时,渗漏增强,因此产量降低现象出现较晚。综上所述,水稻产量与灌水量响应规律表现出高度非线性,且总体下降趋势明显,并随地下水埋深增大表现出滞后现象,能够为优化水稻分区灌溉制度提供理论依据。 5.3 灌溉制度风险决策结果根据式(11)分别计算各年型不同区域不同决策风险偏好下节水效益(C1)、增产效果(C2)和地下水稳定性(C3)三个属性的权重值,基于期望效用函数理论,引入绝对风险回避系数A(W)衡量风险回避程度,A(W)>0为风险规避型;A(W)=0为风险中性型;A(W)<0为风险偏好型,计算结果如图9所示。结果显示,属性权重未知时,不同风险态度会影响各属性权重分布。随着风险态度逐渐转变为偏好型,地下水埋深较浅区域(Ⅰ区)C1属性权重上升,C2属性权重下降,C3属性权重保持稳定;埋深较深区域(Ⅱ区)C1属性权重降低,C2属性权重略微降低,C3权重上升。 图9 各典型年不同区域内不同风险偏好下各属性权重分布 根据各年型各分区不同风险态度的属性权重,结合效用函数,采用有序加权算术平均算子(OWA)对灌溉情景综合效用值进行集结,选取综合效用值最大的灌溉情景为最优灌溉制度,结果见表9。 表9 各年型不同地下水埋深区域的优化灌溉制度 优化后,相比传统雨养种植,平水年每增加100 mm 灌水,水稻产量提高1100 kg/hm2以上,枯水年每增加100 mm 灌水,产量提高1000 kg/hm2以上,Ⅰ区水稻增产效果更显著。通过灌溉措施可以缓解降雨时空分布不均导致的水稻水分亏缺,因此松嫩平原水稻分区灌溉模式具有较大灌水增产潜力,优化后的水稻灌溉制度能实现增产目标。相比传统淹灌[37],优化后的灌溉制度考虑了稻田地下水的补给作用与田间深层渗漏的影响,平水年平均节水22%以上,枯水年平均节水30%以上,在浅埋区(Ⅰ区)节水效果更显著,可节水37.6%以上。相较于灌区现行灌溉制度[37],平水年可节水15%左右,枯水年可达20%。松嫩平原当前种植结构下[1],采用优化后的水稻灌溉制度至少可节水8.3亿m3,减少地下水开采量12%以上。因此,考虑稻田地下水埋深进行分区优化后的水稻灌溉制度,在稳产的同时具有良好的节水控采效果,能有效缓解地下水超采现象,为当地河湖湿地生态系统安全提供保障。 (1)通过2017—2019年松嫩平原北部和平灌区降雨-地下水-产量监测试验与统计分析,揭示了灌区地下水时空动态变化规律,提出了稻田动态地下水埋深条件下的水稻灌溉制度分区优化方法,采用K-Means算法与空间叠加分析方法,确定了和平灌区稻田地下水埋深的分区界限为1.5 m。 (2)采用贝叶斯模式平均(BMA)方法融合AquaCrop、Jensen模型产量模拟系列,提高了动态地下水埋深条件下的产量模拟精度,BMA 产量模拟值与实测值的相关系数超过0.95。通过模拟不同水量分配情景,揭示了各典型年分区灌溉的水稻产量-灌水量差异性响应规律与灌溉增产潜力,为分区灌溉制度优化提供理论基础。 (3)为提高灌溉制度优化结果的合理性,构建了基于区间二型模糊集理论的灌溉制度模糊风险决策模型,引入风险偏好因子刻画决策者的风险态度,提出了适合不同决策者的灌域分区灌溉模式,该模式能够减少稻田灌水量15%~37.6%,减少地下水开采量12%以上。 (4)由于地下水埋深时空差异性大,点尺度历史地下水埋深数据存在局限性,地下水埋深分区结果的有效性受到挑战,因此构建区域地下水埋深实时模拟、预测模型,提高分区结果的有效性,获得更合理的水稻分区灌溉制度,是未来需要完善的重要内容。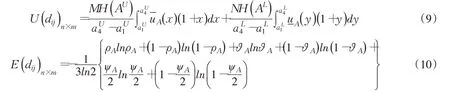
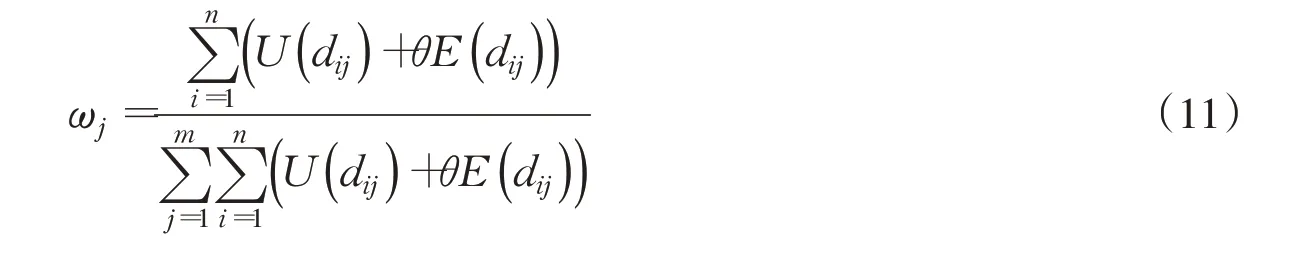

5 结果与分析





6 结论

