基于布谷鸟算法和牛顿法组合算法的6R机器人运动学逆解

赵 瑜

(江苏信息职业技术学院 基础课部，江苏 无锡 214153)

0 引言

精确求解6R工业机器人逆运动学一直是机器人领域的难题[1]。目前，主要有三种求解6R机器人逆运动学的方法：几何解法、解析法和数值法。几何解法具有表达形象、直观的优点，但对于三维空间内机器人的逆运动学问题，该方法求解会变得更加复杂，因此想要得到精确解便非常困难，缺乏通用性[2]。对于机器人几何结构不满足Pieper准则时，采用解析法求解将会异常复杂，无法求解得到封闭形式的逆解。此时，只能采用数值解法求得近似解[3]。

数值方法主要分为两类：直接数值法求解和间接数值法求解。直接数值法求解是根据机器人运动学关系构建迭代方程式，结合数值计算方法，可迭代求解出近似解。这一类方法中，牛顿迭代法[2，4]及其改进算法[5]运用广泛。而间接数值法主要通过将机器人运动学关系进行转化，构造成适当的目标函数，采用智能优化算法搜索求解[6-7]。此外，基于神经网络和训练近似模型的间接方法也有应用[8-10]。然而，直接数值法的迭代求解结果受初始值的设定比较敏感，很容易出现无法收敛的情况。而间接数值法中智能优化算法的迭代后期收敛性较差，求解较高精度的解所需迭代次数较长，神经网络和近似模型算法训练库的生成计算量非常大，且模型建立过程复杂。

由于智能优化算法在全局上具有较强的寻优能力，牛顿迭代法具有收敛速度快、精度自校正的优点。本文提出一种基于智能优化算法和改进牛顿迭代法的组合算法，用于求解一般6R机器人逆解。组合算法通过对目标函数设置阈值，采用布谷鸟算法经少量迭代求得质量较好的初始解，再将该初始解作为初值，使用改进牛顿迭代法求取高精度运动学逆解。最后通过仿真试验和几个智能算法求解对比，验证了该组合算法的有效性。

1 6R机器人运动学建模

根据6R机器人连杆和关节的位置关系，从机器人的底座开始，到末端执行器为止，将各连杆从小到大依次编号，并将基座定义为0号连杆。对于每个关节的编号，规定对于任意连杆i，其靠近基座方向的那一关节编号为i，而远离基座方向的那一端为关节i+1。据此，可通过后置D-H法可依次得到6R机器人的连杆参数，如表1所示。

表1 6R机器人连杆参数

根据上表1中的连杆参数，可以获得末端执行器在基坐标系下的表达式为：

Tend=T1·T2·T3·T4·T5·T6

(1)

上式中：Ti为4×4变换矩阵，表示第i个连杆坐标系与其前一个连杆坐标系的变换关系。变换矩阵是基于齐次坐标变换法得到，其具体表达式如下：

Ti=Rz(θi)·Tz(di)·Tx(ai)·Rx(αi)

(2)

其中各坐标变换矩阵分别如下所示：

求解机器人逆运动学就是在已知机器人末端位置Tend的条件下，求解各个关节转角的过程。定义6R机器人的广义速度V，它是一个6维向量，由角速度ω和线速度v共同组成。则有：

(3)

其中：J(θ)是Jacobian矩阵，该矩阵是一个6×6的矩阵。Jacobian矩阵中的行数表示机器人的自由度数量，列数代表机器人的关节数量。定义微分运动矢量D为

(4)

将上式(4)中对θ的微分改为差分的形式有：

D=J(θ)Δθ

(5)

进而有：

θn+1=θn+D·J-1(θn)

(6)

其中J-1(θ)为Jacobian矩阵的逆，为了避免J(θ)会出现不满秩的情况，采用广义逆矩阵代替。则求解6R机器人逆运动学可以转化求解以下的优化问题：

minf(θ)=‖D·J-1(θ)‖2

(7)

2 组合算法求解

传统的数值迭代算法具有收敛速度快的优势，但在求解机器人逆运动学问题时，此类方法受设定初值的影响较大，容易出现迭代发散的情况。而采用群体智能算法求解机器人逆运动学的主要问题在于迭代后期收敛速度较慢，不能有效满足机器人设定精度要求。但是群体智能算法通过设定一定数量的种群来求解目标函数，其每次迭代都会产生大量新的解，这样便容易获得适合传统的迭代算法的初始解。

结合上述两类算法的优点，在求解6R机器人逆运动学问题时，可以使用群智能算法求解满足一定精度的关节角作为迭代算法的初始值，然后转用牛顿迭代算法迭代求解。基于上述思想，本文采用通过动态调整学习率的牛顿法结合布谷鸟算法形成一种组合算法，用于求解6R机器人逆运动学。组合算法通过设置阈值，先用布谷鸟算法寻得满足阈值条件的低精度初始解，然后通具有动态调整学习率的牛顿法迭代，获得高精度的逆解。

2.1布谷鸟算法

布谷鸟[11](CS)算法是通过对布谷鸟寻窝产卵这一行为模拟提出的一种群体智能优化算法。该算法的理论主要是源于布谷鸟的独特繁殖方式——寄宿式繁殖，以及莱维随机游走策略。上述策略可以抽象成为以下规则：

(1)每个布谷鸟每次只产一个蛋，并将其放入随机选择的鸟巢中孵化

(2)随机选择一组鸟巢，并将最佳的鸟巢保留至下一代

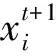
因此，基于上述规则的CS算法其数学表达式如下：

(8)

(9)

(10)

(11)

其中：

(12)

σv=1

(13)

在CS算法中，式(8)用于执行全局搜索，式(9)用于执行局部搜索。

2.2改进牛顿法

牛顿法是具有二阶收敛速度的寻优算法，常用于求解非线性方程组[12]。对于非线性方程F(x)=0，将其近似解记作x0，然后用泰勒公式将F(x)展开，取展开式的线性部分，并令展开式为零，便可得初步求得近似解x1，再在x1处进行泰勒展开，如此往复展开，便可求得满足设定精度的方程解xn+1。这一过程的数学表达式为：

(14)

学习率(Learningrate)是深度学习中重要的超参数，它决定着目标函数能否收敛到局部最小值并控制着收敛的速率[13]。合适的学习率能使代价函数收敛更快，一般地，动态调整学习率能使代价函数更快收敛。常用的学习率衰减方法有分段常衰减、指数衰减、多项式衰减和余弦衰减。

引入上述学习率的思想，结合式(7)，将式(6)改写为以下的迭代形式：

θn+1=θn+Learnn·f(θn)

(15)

其中Learnn表示第n次迭代时的学习率，为了保证逆运动学的求解的精度，设计了一种指数形式学习率衰减策略，其表达如下：

(16)

其中：η0为初始学习率，其值为1；ηt为动态调整参数，其值设为0.001；N为使得迭代至设定精度所设定的总步数。

因此，上述CS和具有动态学习率的牛顿迭代法结合的6R机器人逆运动学组合算法的流程图如图1：

图1 组合算法流程图 图2 IRB4600机器人

为了更好的地评价组合算法在求解机器人逆运动学上的性能，设置布谷鸟算法、鲸鱼算法[14](WOA)和量子粒子群算法[15](QPSO)作为对比。

3 逆运动学求解实例

根据表1所示连杆参数，在MATLAB环境中利用Robotics Toolbox创建IRB4600机器人的仿真模型，如图2所示。

在IRB4600机器人的工作空间内随机生成一条路径，每次在该路径随机取1个点分别用不同的智能算法计算适应度函数(7)。定义末端位置误差为

(17)

设置CS、WOA、QPSO和组合算法的迭代总数均为3000，种群大小均为50，其中组合算法中阈值ε=0.2。在路径上随机选取30个点求解并求其平均值，结果如表2：

表2 不同算法的迭代结果

上表的结果说明，使用CS、WOA和QPSO分别对适应度函数(7)迭代3000步，能使适应度的数值收敛至0.3以下。其中CS和QPSO的收敛结果相差不大，WOA较他们略好。但这三种算法对应末端执行器的误差均在100mm以上，这完全无法满足机器人使用时的精度要求，这表明仅仅使用智能优化算法来求解，存在求解精度低，结果不可靠的问题。而采用本文所提出的组合算法，在迭代3000步后能使适应度函数的值迭代至10-10数量级，同时末端执行器的精度保证在10-9数量级，较布谷鸟、鲸鱼算法和量子粒子群算法提升明显。够满足工业应用对位置的高精度要求。

现以机器人某一时刻在生成路径上的位姿为例，其在基坐标系下的矩阵为：

分别采用布谷鸟算法、鲸鱼算法、量子粒子群算法和组合算法对上述位置所对应的适应度函数进行求解，图3至图6分别为CS、WOA、QPSO和本文所述算法的收敛曲线。

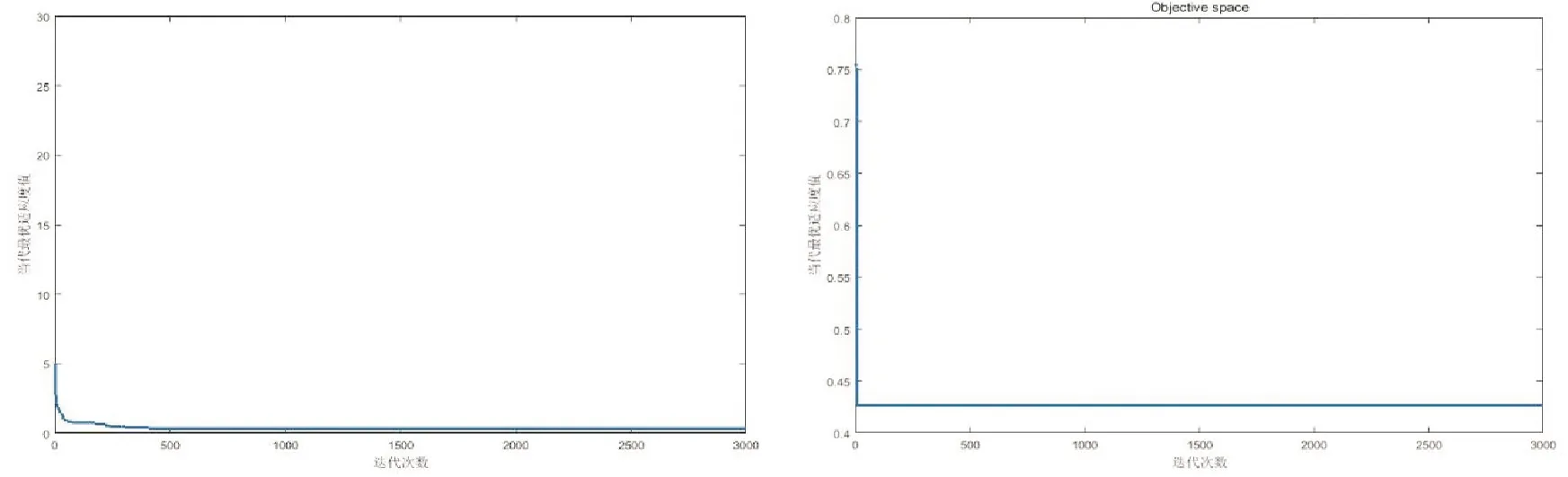
图3 CS迭代求解适应度曲线 图4 WOA迭代求解适应度曲线

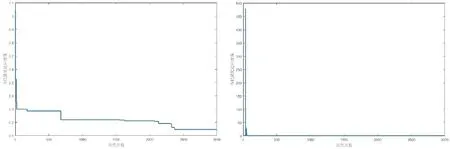
图5 QPSO迭代求解适应度曲线 图6 组合算法迭代求解适应度曲线

从上述收敛曲线可以看出，使用各种智能算法迭代，适应度曲线在前期快速衰减。其中鲸鱼算法和布谷鸟算法在前期的收缩过程中寻优能力较强，使目标函数值下降较快。但是，不同的智能算法的收敛精度差异明显，鲸鱼算法能将目标函数(7)的值收敛至0.43左右，量子粒子群算法能使其收敛至0.2左右，由表2的结果可知两种算法的效果并不理想。对于布谷鸟算法，其收敛精度较鲸鱼算法和量子粒子群算法较好，收敛时的适应度函数值为0.149，根据表2所示的结果可以得出，这一数量级下的适应度函数值还无法满足末端执行器对位置精度的要求，因此单纯地采用智能算法求解，效果并不理想。

图6为组合算法迭代过程中适应度函数曲线。看出在前期布谷鸟迭代过程中会出现适应度函数值较大的情况，但是当适应度函数值达到阈值后，转用牛顿迭代法求解时，其收敛速度较布谷鸟、鲸鱼算法和量子粒子群算法相比更快，而且收敛精度更高。为了更加清晰地体现组合算法求解过程中的适应度的变化，表3显示了不同迭代解精度与迭代所用次数及末端执行器的误差大小。

表3 组合算法求解过程的精度与误差

根据表3的结果可以看出，使用布谷鸟迭代至21次时便已经达到设置的阈值，此时的末端执行器的位置误差仍然较大，但是当组合算法转为改进牛顿法迭代后，能够在70步左右将末端位置误差减小至1mm一下，此后的迭代过程中，适应度函数值及对应末端位置误差快速减小，最终获得了高精度逆解。这说明组合算法中采用布谷鸟算法求解能获得质量较好的初值。指数函数形式的学习率衰减策略能有效地加快牛顿法的迭代精度，从而获得较高的质量的逆解，执行器的末端精度可以控制在10-9(mm)数量级。

4 结论

为解决6R机器人逆运动学高精度求解，结合直接数值法和间接数值法各自的优点，提出了一种组合算法。组合算法通过设置一个合适阈值，采用布谷鸟算法求解获得一个低精度解，并将该低精度解作为牛顿迭代法的初始解，然后采用一种指数形式的学习率衰减策略动态调整牛顿法迭代，从而快速求得高精度的机器人逆解。在MATLAB环境下进行了仿真实验，结果表明:组合算法求解得到的平均误差在10-9数量级，具有较高精度，能够满足工业应用的要求。