基于一维椭圆问题的瀑布型两层算法研究
黄爱梅
(福建船政交通职业学院,福建 福州 350000)
0 引言
在工程与物理领域中,偏微分方程是最为重要的数学模型,解决了弹性力学、时间相关问题、流体力学和积分方程等方面的科学问题[1]。多重网格法是求解偏微分方程数值解的有效方法之一,具有收敛速度快和计算工作量少等优点[2]。然而,多重网格法并不适用于求解椭圆界面问题,无法准确求解界面差分格式的离散方程,需结合曲面信息和跳跃条件构建插值算子进行求解[3,4]。在求解偏微分方程时,通过插值算子处理,拟补了传统有限差分法求解的矩阵大型、稀疏、病态等缺陷[5]。此外,许多数学家根据不同的插值和限制算子衍生出多种不同形式的瀑布型多重网格法(CMG)来解决椭圆方程的数值问题[6,7]。例如,贾学良等采用次插值作为插值延拓算子构建了新的瀑布型多重网格法,在容许误差精度能准确求出椭圆界面数值[8]。考虑到一个好的插值算子能为细层提供较好的初始值,进而可以减少磨光迭代步数[9]。本文采用牛顿二次插值代替传统的线性插值,构造了一种新瀑布型多重网格法,并给出数值算例验证算法的有效性。
1 椭圆模型问题的传统解法与新型
1.1椭圆型问题的差分离散
考虑如下一维椭圆型问题
(1)
其中p(x)∈C1[a,b];r(x);p(x)≥pmin>0,q(x)≥0。α和β为给定的常数。
首先将求解区间[a,b]进行剖分,为简单起见,将区间[a,b]分成N等份,分点为xi=a+ih(i=0,1,…,N),h=(b-a)/N,xi称为网点(或结点、节点),h称为步长。然后将微分方程(1)在网点xi处离散化。设xi(i=0,1,…,N-1)是任一内结点。在点xi处,对充分光滑的函数u,根据精度为o(h2)的中心拆分公式有[10]

(2)
(3)
(4)
(5)

(6)
将式(3)-(6)代入式(1)式中,即得二阶精度的差分方程
(7)
边值条件对应的差分方程为
u0=α,uN=β
(8)
将式(7)和式(8)写成如下矩阵形式
Au=g
(9)
其中
(10)
其中g=(g1+α1α,g2,…gN-2,gN-1+cN-1β)T;u=(u1,u2,…,uN-1)T;
可以验证,当h充分小时,关系式|bi|≥|ai|+|ci|,i=2,…,N-2,|b1|>|c1|,|bN-1|>|aN-1|成立,也即矩阵A具有严格对角占优性。实际上后两式显然成立,对第一式,注意h充分小及p(x)≥pmin,必有
因此A是非奇异矩阵,差分方程(9)有唯一解。
1.2瀑布型多重网格法
多重网格法也称为多格子方法,是目前应用于大型科学计算的一类有效的、新颖的计算方法,它在理论上是最优阶的方法,近年来由于大型计算机的迅速发展和功能的日趋完善,从而使得多格子方法作为最优阶的算法从理论变为现实,使得许多生产实践中的实际问题,尤其是求解椭圆型方程边值问题,其优点在于不要求粗网格校正和限制算子。
Aiui=Fi,i=1,2,…,H
(11)
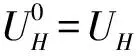
(12)


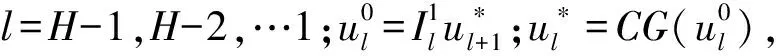

可以看到,网格层从ZH到Z1,只用了插值与迭代,没有限制,校正及后磨光,程序比较简单,并且总的工作量只有O(n)。
1.3新瀑布型两层网格法
瀑布型多重网格法的思想是将粗层上的解逐层插值、磨光,直至最细网格层为止,为了减少中间网格上的计算量,本文采用步长为4h和h,离散问题(1),形成粗细两层网格,而不需要生成步长为2h的中间网格,然后再将粗网上的解插值到细层,提出了瀑布型两层网格法。
采用一种有效的插值算子,给出细层上一个较好的初始值,进而减少磨光迭代步数,可以加快瀑布型多重网格法的收敛速度。由于通常线性插值效果一般,导致采用线性插值的瀑布型多重网格法的计算精度一般,为了提高计算精度,本文引入牛顿二次插值作为插值算子,构造了一种新的瀑布型两层网格法。
1.3.1牛顿二次插值算子的构造方法
在讨论牛顿插值公式之前,先介绍与之相关的差商的概念及其性质。
设已知x0,x1,x2及f(xi)=yi,i=0,1,2,f(x)在xi点的零阶差商f[xi]记为
f[xi]=f(xi)
(13)
f(x)在x0,x1两点的一阶差商f[x0,x1]记为
f(x)在x0,x1,x2三点处的二阶差商f[x0,x1,x2]记为
利用差商,来构造牛顿二次插值公式。
f(x)=f[x]=f(x0)+(x-x0)f[x,x0]
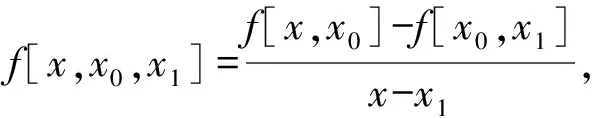
f[x,x0]=f[x0,x1]+(x-x1)f[x,x0,x1]
依次类推,有
f[x,x0,x1]=f[x0,x1,x2]+(x-x2)f[x,x0,x1,x2]
从而有
(14)
将(14)式中后一式代入前一式便有
f(x)=f[x0]+(x-x0)f[x0,x1]+(x-x0)(x-x1)f[x0,x1,x2]
牛顿二次插值公式为
N2(x)=f[x0]+(x-x0)f[x0,x1]+(x-x0)(x-x1)f[x0,x1,x2],
即
把x0,x1,x2及f(xi)=yi,j=0,1,2代入上式得
(15)
所以,式(15)即为牛顿二次插值公式。
1.3.2新瀑布型两层网格法
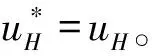
2 数值实验
为了验证本文算法的有效性与准确性,分别采用如下两个算例进行分析。对以下的两个算例,均采用中心差分离散,光滑算子为CG迭代,迭代终止条件为‖uk-uk-1‖<10-6,其中k为迭代步,“迭代步”栏中为最细层的迭代步数,“能量误差E”为采用不同的插值算子的瀑布型多重网格法得到的数值解与问题的真解的能量误差。
算例1.-u″(x)+u(x)=f,x∈[0,1],u(0)=u(1)=0。
其中f=(-4x-2)ex-x2+2,真解u=x2(ex-1)
如表1所示,算例1在进行迭代步数6和构建8192个粗层点数与32767个细层点数后迭代终止。牛顿二次插值的能量误差均小于线性插值的能量误差,且迭代步数也相对少,节省了运算的时间。
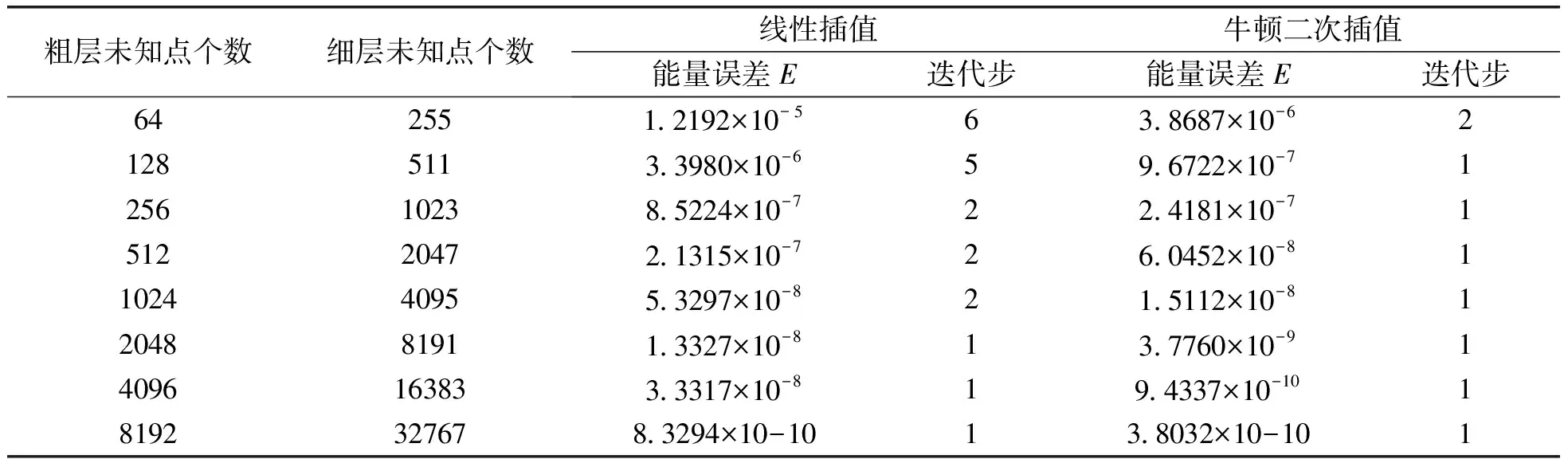
表1 采用不同的插值算子的瀑布型两层网格法对算例1的数值结果
算例2.-u″(x)+u(x)=f,x∈[0,1],u(0)=u(1)=0。
其中f=(-2+2x2)sinx-4xcosx-x2+2,真解u=x2(sinx-1)。
从表2可以看出,实验结果与算例1类似,对于瀑布型二层网格法,采用牛顿二次插值作为插值算子比线性插值的效果要好一些,甚至能量误差相差一个数量级且无限接近问题的真解,充分说明了牛顿二次插值的瀑布型二层算法具有计算精度高,迭代步数少的优点,因此,本文设计的新瀑布型两层网格法,进一步丰富了求解一维椭圆型问题数值算法。
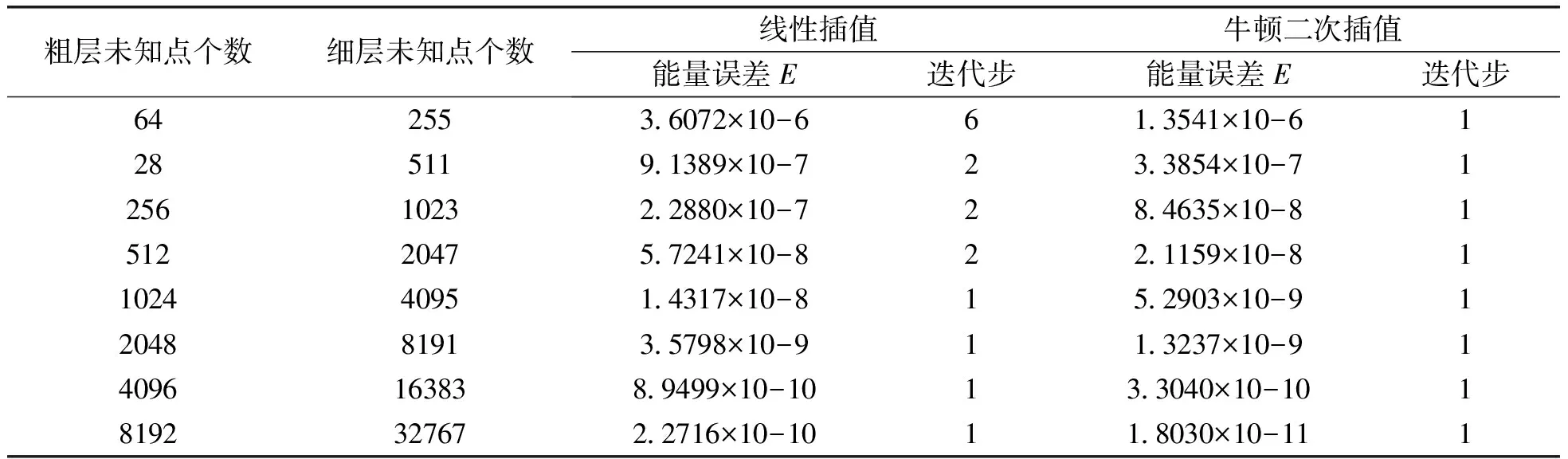
表2 采用不同的插值算子的瀑布型两层网格法对算例2的数值结果
3 结论
对于一维椭圆问题的离散方程组,通过比较牛顿二次插值和线性插值作为插值算子运算过程构建了瀑布型二层网格法。在相同的参数限制条件下,基于牛顿二次插值算子的瀑布型二层网格法具有更低的能量误差,即算法的精度更高。

