用小波熵测度Lorenz系统准周期特性

李 伟，梁雯君，史 韬，邓 胜，杨建平

（井冈山大学电子与信息工程学院，江西,吉安 343009）

0 引言

Lorenz 模型是1963 年由美国气象学家洛伦兹在研究区域小气候时求解出来的一个数学模型，它是非线性系统研究中常用的一个经典例子。目前已有很多Lorenz 系统的动力学特征研究成果，如采用线性稳定性分析（局部稳定性分析）方法，能分析定点及其邻域的性质，但没有涉及系统在整个相空间是否一定收敛（有界）的全局稳定性问题；用Lyapunov 指数定量地描述Lorenz 系统相空间相邻轨道随时间收敛（或发散）的平均速率[1]，可得到系统具有全局稳定性，最终收缩到捕捉区内，并形成一个不变的集合，即吸引子；另外，在非线性动力学传统分析方法上有功率谱、重现图形、Poincare截面图等，这些方法在分析系统时具有通用性，分析非线性系统无独特优势。为研究非线性系统演变的准周期性特征[2-3]，多采用非线性系统的分析方法，如近似熵是统计量化的非线性动力学参数，能够较好地表达Lorenz 系统复杂特征[4-5]，但没有将Lorenz 系统的局部特征和整体演变过程结合起来；如文献[6]采用三次粗粒化方法，运用动态、粗粒化的非线性时间序列分析方法（Lempel-Ziv 复杂度），分析了Lorenz 模型的复杂度演变特征，但粗粒化描述的Lorenz 系统其运动学演变特征缺乏细腻、连贯、精准性。

本研究从时频分析出发，应用小波变换在时域和频域同时具有定位分析信号的能力，突出系统的突变信息，并且将描述系统复杂度的信息熵理论和小波分解结合起来，形成Lorenz 系统测度的小波熵方法，将Lorenz 系统的局部突变和整体演变进行统筹考察，呈现其准周期运动特征。该方法非常适合于分析非平稳信号、非线性动力学系统的时间序列，能够反映多频率成份信号的混乱程度并提供时间序列的动力学演变特征，已经在生物医学、机械故障诊断等领域的应用中取得了一定的成果[7-11]，能够为Lorenz 混沌系统的动态复杂度计算提供一种时——频分析手段。

1 时间序列的小波分解

具有多分辨率的小波变换算法是利用正交小波基（或双正交）将信号分解成不同尺度的多个分量，此过程可理解为循环使用一对高通滤波器与低通滤波器，逐级对时间信号进行滤波，经过高通滤波器获得信号的高频细节分量，通过低通滤波器生成信号的低频粗略分量。分解后得到的信号分量所占频带宽度相同，均占原信号频带宽度的二分之一，每一次分解后，将原信号的采样频率减少一倍；下一层次的分解是对低频分量重复上述分解（滤波）过程，最后得到下一层次的两个分解细节分量。

2 小波熵的准周期测度

用Shannon 信息熵描述Lorenz 系统运动的不确定性。例如，对于一个仅有有限个样本值的随机变量，用X 表示其状态特征，样本值为xi的概率

小波变换具有在时域和频频同时局部化能力，将Lorenz 系统时间序列的时频分支序列与信息熵相结合，可以得到Lorenz 系统时间序列的小波熵值——小波熵测度。设其在m个尺度上的小波能量为：

图1 为由两种周期成分仿真构成的一信号，前500 个点为长周期，后500 个点为短周期。对照其相应的小波熵序列图，从图中可以看出：周期较大时小波熵趋于零，周期较小时小波熵更大，中间过渡部分小波熵出现最大值，即准周期小波熵复杂度的大小与窗口内序列准周期的平均周期一致，可以用运动复杂度来分析Lorenz 系统的准周期的运动特征，刻画系统长时间的演变特征。

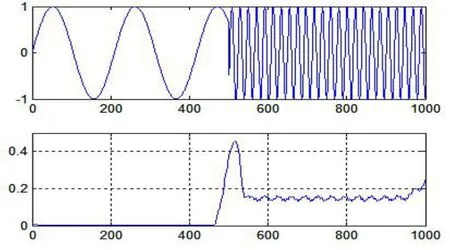
图1 长、短周期的小波熵序列演变特征Fig.1 Evolution characteristics of wavelet entropy series with long and short periods

3 Lorenz 系统的时间序列及其小波熵测度

3.1 Lorenz 系统的运动特征

采用四阶Runge-Kutta法求解该微分方程组，并调用MATLAB函数ode45进行计算，时间范围取0～60s，求得x、y、z三个分序列的各3285点。图2为x分量的部分时域图，从图中可看出该分量围绕着x轴上的两点振荡运动，正方向在x=8附近，为系统的p+吸引子，负方向在x=-10附近，为系统的p-吸引子；图3所示为其混沌吸引子图，系统运动过程中局限在相空间中的有限区域内，即绕p+吸引子（或p-吸引子）运动一段时间后变化到绕p-吸引子(或p+吸引子)运动，为非周期的混沌运动，但又有周期性特征，即各阶段由类似的、但又不同的准周期运动交替构成。

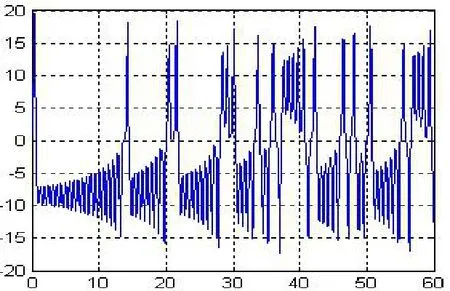
图2 Lorenz系统的部分时域图Fig.2 Partial time domain diagram of Lorenz system

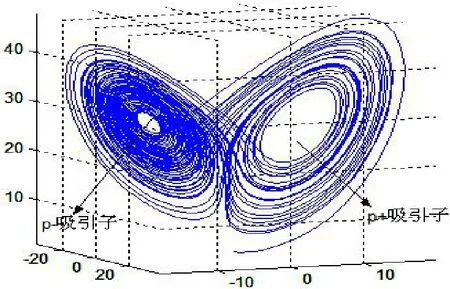
图3 Lorenz系统的混沌吸引子Fig.3 Chaotic attractor of Lorenz system

3.2 准周期测度的计算

考虑正交小波函数的多样性，选用正交性好的db系列小波，利用其紧支撑和多尺度分析的特点，来描述系统的准周期测度。

计算方法：（1）采用db6小波对系统的时间序列进行三层小波分解，分解与重构后得a3、d3、d2、d1等四个分支序列。（2）采用滑动窗口的方法计算小波熵，滑动步长取1（平滑效果好，但计算量偏大），即对四个分序列选取窗口宽度为W，进行长度为W/2的、对称的、一维扩展，再用一个宽度为W的时间窗从扩展后四个分信号的第1点开始截取长为W的一段，依照小波熵定义可求出此时间窗的小波熵值，并将此小波熵值赋给时间窗内的第W/2+1点（对应原Lorenz时间序列的第一个点）；（3）将时间窗向右移动一个点，得到四个分支序列第二窗口的四段数据，并求得第二个点的小波熵值；（4）依次循环下去，可得到整个序列各个点对应的小波熵值，即为所求的小波熵复杂度序列，用来测度准周期的演变特征。

为观察混沌系统的较长时间内演变特征，用Runge-Kutta法计算系统时间序列时取360 s，得到20869点的x、y、z三个序列，分别计算x、y、z三个序列的小波熵序列，三者情形一致。文中以计算x分量的运动复杂度为例，分别取窗口宽度为W=600，W=800和W=1000， 求得Lorenz模型的x分量在各窗口中的运动复杂度序列，如图4所示，对于不同的窗口宽度时，系统的复杂度特征基本一致，三个小波熵序列运动复杂度的变化特点都呈现了Lorenz系统运动过程中的内在特征——小波熵测度的演变特征，鉴于此，下面的分析中均采用W=600进行分析。

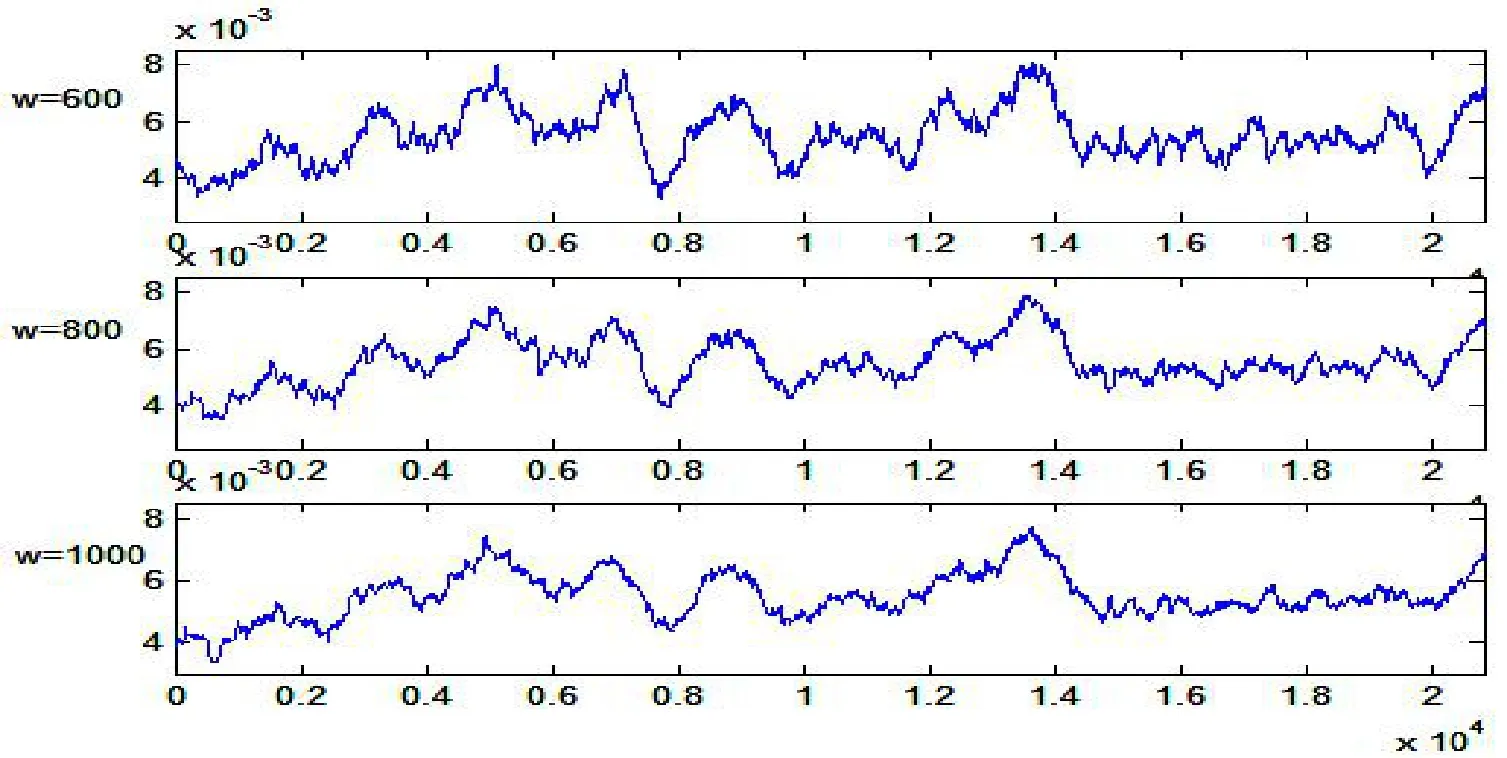
图4 x分量不同窗口宽度的小波熵复杂度Fig.4 Wavelet entropy complexity of x component with different window width

在图4中，小波熵运动复杂度序列包括很多极大值、极小值，这些极大值、极小值的出现与系统绕p+吸引子或p-吸引子的振荡有关，一个振荡来回为一个准周期。（1）根据图1长、短周期的演变特征可知这些极大值、极小值的出现与准周期的长短有关；（2）小波熵序列的波形为大小不一、形状相似、山峰状的循环窗口组成，也具有准周期性。

3.3 运动复杂度的周期性描述

图5为x分量的360 s时域图及W=600时的小波熵复杂度序列，图中的最小值点序号为7818，小波熵值为0.0033，最大值点序号为13757，小波熵值为0.0081，为探讨最小、最大小波熵值点的准周期动力学特征，将最小、最大小波熵值所对应窗口的时域图分别于图6、图7中画出。

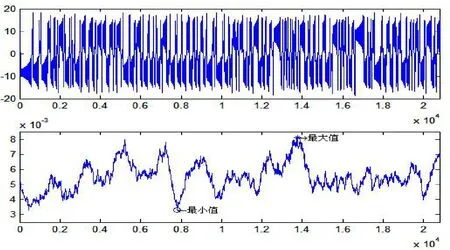
图5 小波熵测度的最小、最大值（w=600，点数为20869）Fig.5 Minimum and maximum values of wavelet entropy measure(w=600,number of points is 20869)

图6中最小小波熵值对应x分量的时域窗口为［7518 8118],图7中最大小波熵值对应x分量的时域窗口为[13457 14057]。对照长、短周期的小波熵序列演变特征分析lorenz系统的准周期特性。最小小波熵值的系统特征：（1）最小值所对应窗口的平均准周期最长；（2）最小值点两边lorenz系统的平均准周期无突变，两边有非常对称的准周期运动特性；最大小波熵值的系统特征：（1）最大值所对应窗口的前半个窗口表现为多次绕p+吸引子或p-吸引子振荡一次便转为绕p-吸引子或p+吸引子的振荡，即平均准周期最短；（2）最大值两边Lorenz运动的准周期发生突变；左边为短平均准周期，右边为长平均准周期。因而，lorenz系统的平均准周期的演变过程总是伴随着小波熵序列的由极小值变化到极大值、由极大值变化到极小值，是准周期长短、对称的演变过程，包括准周期的缓慢演变、准周期的突变等过程。

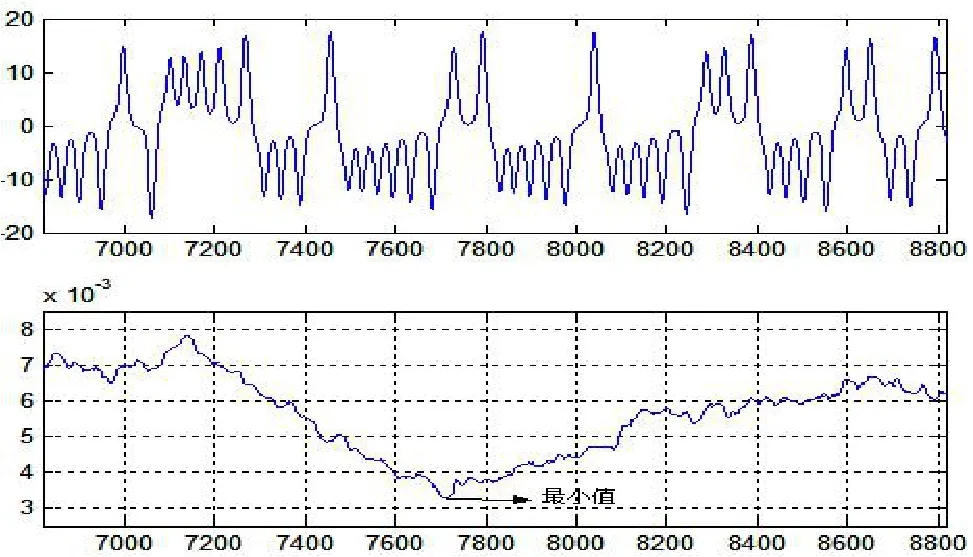
图6 x 分量最小小波熵值与时域运动特征对照Fig.6 Comparison of minimum wavelet entropy of x-component and motion characteristics in time domain

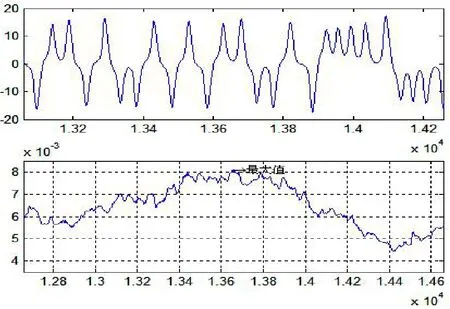
图7 x 分量的最大小波熵值与时域运动特征对照Fig.7 Comparison between maximum wavelet entropy of x component and time domain motion characteristics

4 结论

本研究利用Runge-Kutta法求解Lorenz系统的微分方程得到其时间序列，运用小波熵复杂度算法，计算并分析了其时间序列的小波熵测度，计算的复杂度序列反映了Lorenz系统的演化特征，x，y，z三个分量的复杂度序列均具有混沌性质，是由许多大小不一、形状相似的循环窗口组成，反映了Lorenz系统内在的准周期特性；研究小结：（1）各分量长时间连续围绕p+吸引子振荡时及频繁在p-吸引子和p+吸引子之间来回振荡时，小波熵测度出现极大值；（2）各分量长时间连续围绕p+或p-吸引子振荡时，小波熵测度出现极小值；（3）小波熵值在极大值和极小值之间上下振荡，变化过程表征着Lorenz系统准周期的演变特征，因此系统的演化可以通过时间序列的复杂度特性来揭示其动力学结构特征，此方法可以应用到观测数据的动力学分析，通过计算数据的小波熵复杂度反演系统的演变特性。