数学问题解答
2021年7月号问题解答
(解答由问题提供人给出)
2611设△ABC的外接圆半径,内切圆半径,三边长分别为R,r,a,b,c,三个内角∠BAC,∠ABC,∠ACB对应的旁切圆圆心分别为D,E,F,证明:
(安徽省岳西县汤池中学 苏岳祥 杨续亮 246620)
证明设旁切圆⊙D,⊙E,⊙F的半径分别为rA,rB,rC.如图,∠BAC对应的旁切圆⊙D和AB,BC,CA相切于点M,H,N,
则有DM⊥AB,DH⊥BC,DN⊥AC,

DM=DH=DN=rA,
故有A,M,D,N四点共圆,且AD为直径.
由托勒密定理有
AD·MN=DM·AN+DN·AM
=rA(AN+AM),
易知AN+AM=AB+BM+AC+CN
=AB+AC+BH+CH
=AB+AC+BC=a+b+c.
在△AMN中由正弦定理可得
因此
a·AD2=2RrA(a+b+c).
同理可得
b·BE2=2RrB(a+b+c),
c·CF2=2RrC(a+b+c).
以上三式相加可得
a·AD2+b·BE2+c·CF2
=2R(rA+rB+rC)(a+b+c).(1)


在(2)中由正弦定理可得
由三角恒等式
有

由三角恒等式
可得
同理可得
rA+rB+rC-r

所以rA+rB+rC=4R+r, (3)
把(2)式和(3)式代入(1)式可得

由欧拉定理可得R≥2r,



图1

图2
(湖北省潜江市江汉油田教育实业集团教科院 舒云水 433124)
证明⊙I和三个旁切圆与各边的一些切点如图2所示,连接OA,OB,OC,OQ,OM,OW,由题意知O1在OA上,O2在OB上.
因为CM,CW是⊙O的切线,
所以CM=CW.
同理可得AM=AQ,BW=BQ,AD=AE,
BD=BF,CE=CF.
设AB=c,AC=b,BC=a,△ABC,△ACD和△CDB的面积分别为S,S1,S2.
因为CM=AC+AM=AC+AQ,
CW=BC+BW=BC+BQ.
所以CM+CW=AC+AQ+BC+BQ=a+b+c.


所以
S△ABC=S四边形MOWC-(S四边形MOQA+S四边形WOQB)
同理可得
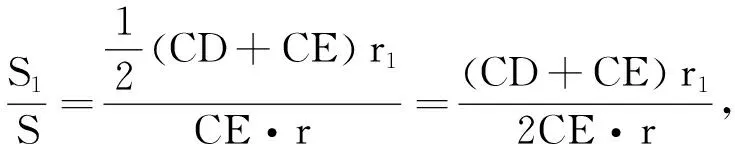




(四川省成都华西中学 张云华 610051)
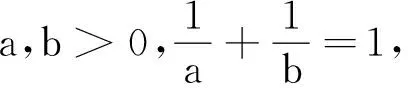


⟺5(ab)2+4≤5ab+(ab)3
⟺0≤(ab)3-5(ab)2+5ab-4
⟺0≤(ab-4)[(ab)2-ab+1]


(江苏省徐州市第一中学 张培强 221140)
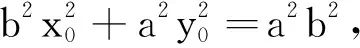
设M(x1,y1),N(x2,y2),




得(a4+b4)x2+2a3(by0-ax0)x
+a2(by0-ax0)2-a2b4=0,





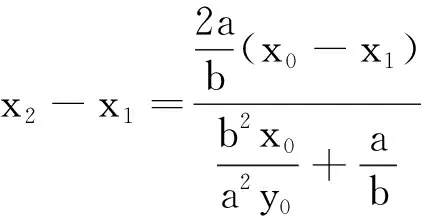
不妨设点P在x轴的上方,则点P在直线MN的上方,所以△PMN的面积


当点P在x轴上时,易得△PMN的面积

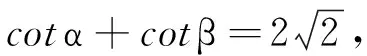

(河南省方城县教研室 邵明宪 473200)
解作PE⊥DC于E,连结PD,PC,则由题意,PE⊥平面ABCD,
且∠APD=α,∠BPC=β.
又AD=BC=1,

记DC的中点为O,以O为原点,直线DC为x轴建立平面直角坐标系xOy(图略),
则点P的轨迹方程为
从而
故

2021年8月号问题
(来稿请注明出处——编者)
2616平面上给定n个点,任意三点不共线,过任意两点作直线.已知任意两条直线既不平行也不垂直,过这n点中任意一点向另外n-1个点的连线作垂线,则所有这些垂线的交点(不包括已知的n个点)的个数至多有________个.
(江苏省常熟市中学 查正开 215500)

图1
2617已知如图1,点A在⊙O上,点D在⊙O外,过点D作⊙O的割线DB2B1、DC2C1.连接AB1、AB2、AC1、AC2、AD,连接B1C1、B2C2分别与AD交于点E1、E2.求证:
(北京市朝阳区芳草地国际学校富力分校 郭文征 郭璋 100121)
2618在△ABC中,证明:
(2)4cosAcosBcosC-(sinA+sinB+sinC)2+(1+cosA+cosB+cosC)2=0;
(3)[-6-2(cosA+cosB+cosC)]·
(华中师范大学国家数字化学习工程技术研究中心 彭翕成 430079; 江苏常州九章教育科技有限公司 曹洪洋 213002)

(安徽省枞阳县宏实中学 江保兵 246700)
2620已知a,b,c为正数,且abc=1, 求证:
a2+b2+c2+6≥3(a+b+c).
(湖北省宜都市一中 刘宜兵 廖全清 袁昌芹 443300 )

