指向“学会思考”的培养路径
——以创新“中考数学复习”为例
张兆驹
(江苏省连云港外国语学校 222006)
1 问题与思考
“学会思考”是学生“学好数学”的动力体系,是一种内在的稳定的认知心理品质,是创新意识培养的“发动机”.《义务教育数学课程标准(2011年版)》明确指出,创新意识的培养是现代数学教育的基本任务,应体现在数学教与学的过程之中.学生自己发现和提出问题是创新的基础;独立思考、学会思考是创新的核心;归纳概括得到猜想和规律,并加以验证,是创新的重要方法.创新意识的培养应该从义务教育阶段做起,贯穿数学教育的始终.为此,教思考、教会思考、教学生学会思考成为课堂的“重头戏”.
本文以中考数学复习为思维运行载体,展现学生“学会思考”的路径方法及其价值思想体系,在“有用组合思维”的参与下,落实学会学习、学会思考、学会成长、学好数学的课程教育目标.
2 方法与路径
2.1 借助思维导图,畅通思考途径
思维导图是概念“来龙去脉”的思考线索,是“学会思考”的思维支点.借助“思维导图”(思维概念图),创设符合学生实际需要的整体知识结构,让知识有源头也有方向.在教材的使用中,我们可以挖掘出适合孩子认知特点和认知基础的知识和问题,引导他们在宽松的氛围中感受学习的乐趣,才能有意识的培养孩子创新的动力和欲望.
例如,在备课组的一次集体研讨中,关于中考四边形复习的内容,从边、角、对角线等不同角度来阐述四边形的发生、发展过程,由简单到复杂,由一般到特殊,呈现知识的脉络,清晰而生动(见图1).
案例1 思维导图
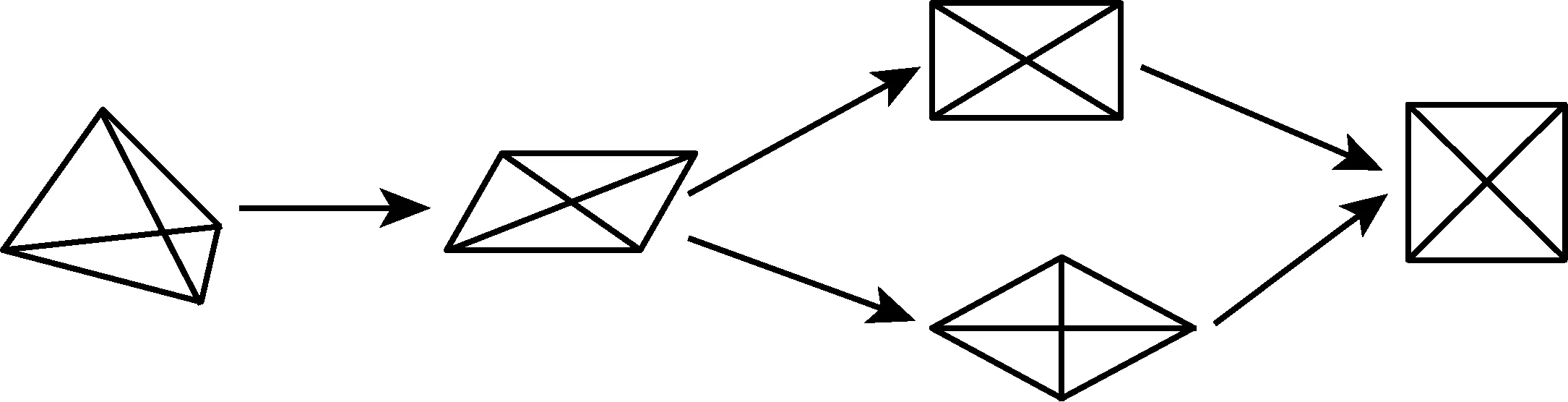
图1
在课堂教学实施过程中,首先,让各小组展示自己绘制的思维导图,呈现该小组的绘图思路;其次,通过讨论再对本小组绘制的思维导图进行修改完善,让原来的思维导图的质量得到明显提升,从而大大加深学生对思维导图的理解和认识,也深化了对知识点的认识和理解;最后,教师对前面建构思维导图的过程进行点评,全班有几个小组,就会有几个思维导图“作品”,各个思维导图的形式、角度可能不一,教师要对其优点进行充分肯定,对重难点问题进行有针对性的评价和建议,加深学生对重难点知识的理解,扫清思考问题的障碍.
课堂教学中,学生展示、修改的思维导图始终围绕定义、性质、判定来建构知识体系,进一步厘清了特殊四边形“家族”中各成员的包含关系(譬如,矩形和菱形的公共部分是正方形等),知道概念的来龙去脉(譬如,有一组邻边相等的矩形是正方形;有一个角是直角的菱形是正方形);让学生从“对称性”和“事实概念”的角度理解特殊四边形的意义(譬如,对角线垂直的矩形是正方形;对角线相等的菱形是正方形),形成概念图及其各要素的结构关系.正是思维导图,将学生已有的知识结构化,具有“手中握无限,刹那成永恒”的整体感,这就是学会思考、教好思考的表现.
2.2 构建基本模型,激发思考兴趣
培养兴趣,聚合思维,就要让学生拓宽知识面,认识客观事物,深入理解所学知识,理解事物的本质属性.要注意沟通知识间的本质联系,抓住知识间的连接点,这样不但可以使学生逐步学会通过现象抓住本质,培养思维的深刻性,而且还激活了学生原有的知识结构,运用迁移解决问题,顺利完成认知建构.因此,教师要设计类似题型的练习,沟通知识间的内在联系,拉伸思维的宽度.
案例2 “K型相似”

图2-1

图2-2

图2-3
复习相似知识点时,选取代表性的“K型相似”为出发点,设计以下三个小题:
(1)如图2-1,有一直角三角板ABC的直角顶点C放置在水平面上的直线DE上,其中AC=5,BC=10,过A、B分别作DE的垂线,垂足为D、E,若AD=3,你能求出BE的长吗?试试看.
(2)如图2-2,过A、B分别作DE的垂线,垂足为D、E,若AD=3,BE=8,DE=10,你能在线段DE上找一点C,使△ADC与△CEB相似吗?你能找几个?
(3)如图2-3,过A、B分别作DE的垂线,垂足为D、E,若AD=3,BE=t,DE=10,若只能在线段DE上找到一个点C,使△ADC与△CEB相似?你能求出t的范围吗?
课堂教学中,老师将一个直角三角板摆放在黑板上,过直角顶点任作一条直线(在直角三角形的一侧),再通过两个直角顶点作该直线的垂线,让学生观察其中有相似三角形吗?引入过程在黑板上和学生一起操作(其他学生在纸上操作),结论和学生一起探讨,学生积极性很高.主要有两个原因:一是学生动手操作熟悉的三角板,感觉非常亲切;二是学生发现任意转动中结论是不变的,感觉非常神奇有趣.
“学会思考”是以参与量为“拐点”的.学生会主动地参与其中,发挥自己的天性畅所欲言,进而发表自己的观点,培养独立思考的能力.通过该题的教学我们发现,从最初基本的相似模型出发,学生由基本的框架构建到搭建桥梁,显得非常自然,通过动点C的移动,创造了想象的空间,学生由基本的模型转而上升到如何处理分类的情况,正反夹击,直击本质,拉伸了学生思维的宽度,也较好地引导了学生分析和处理问题的更一般的方法,这就是会思考的具体表现.
2.3 实施求异思维,引导换位思考
求异思维本身就是一种换位思考,而高效课堂的换位思考往往落地于“一题多问”.教学中,要在掌握常规的基础上鼓励学生突破常规,敢于设想创新,敢于标新立异.例如,通过“一题多解”、“一题多问”的训练,鼓励学生从不同角度去思考和判断问题,提出新设想,探索新路子,以利于学生求异思维的发展,拓展创新思维的广度.
案例3 旋转运动

图3-1
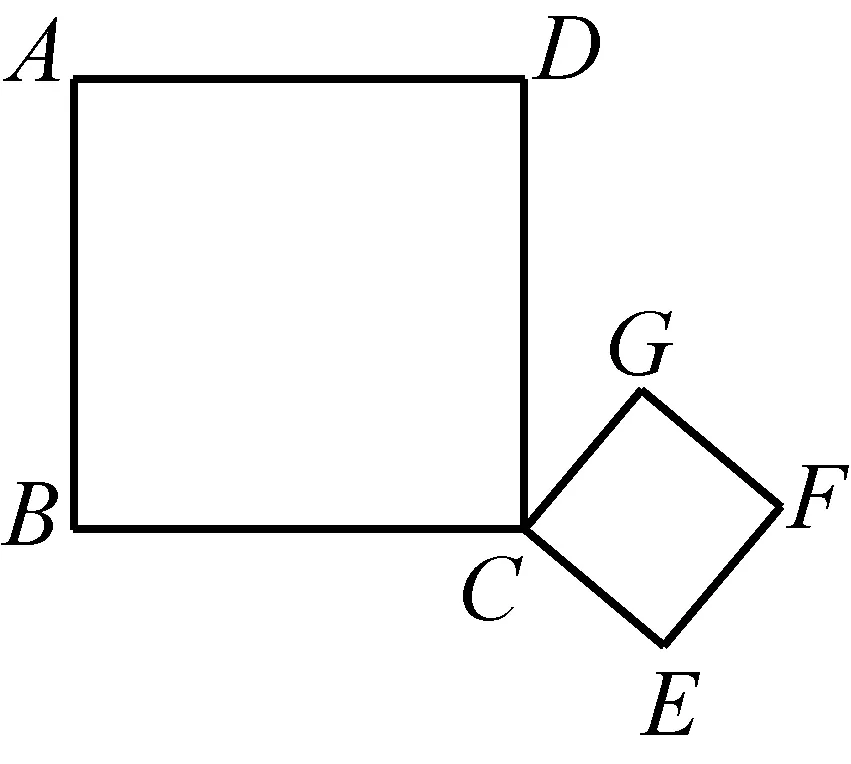
图3-2
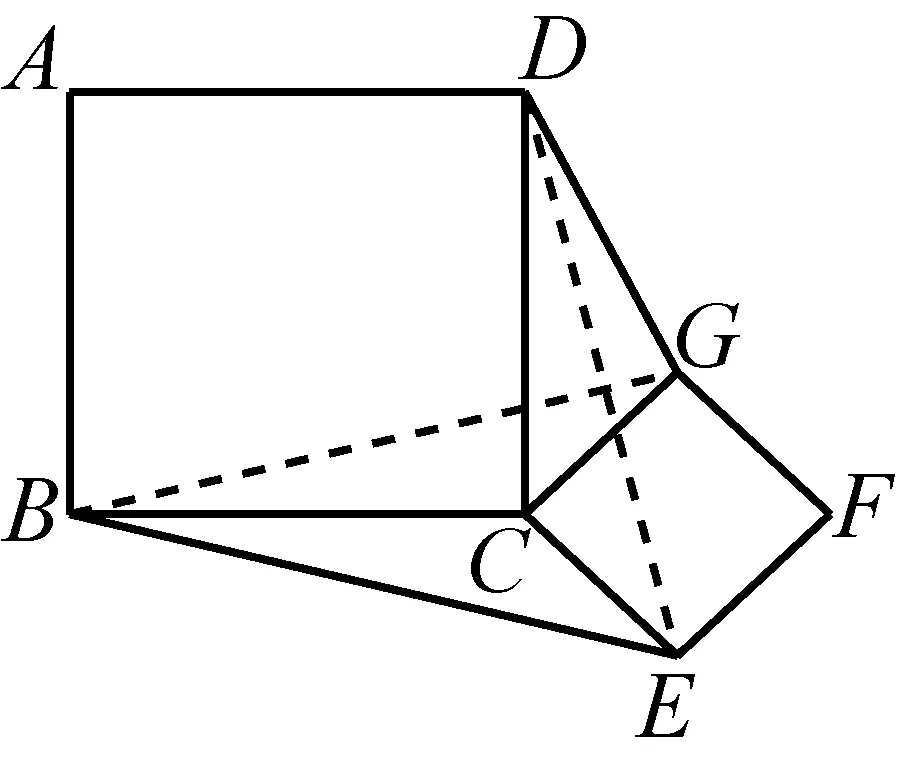
图3-3
四边形复习时,在考虑学生的不同层次和水平时,我们设计了一个关于正方形运动的题目:
如图3-1,当正方形ABCD与正方形CEFG有公共顶点C,并且点B、C、E在一条直线上,点G在CD边上,请你连结出两条线段(正方形相等的对角线除外),使得它们相等.
你连结出的线段除了相等,还有什么特殊的关系吗?
如图3-2,如果绕点C转动其中一个正方形,上述结论还成立吗?
如图3-3,如果两正方形的边长分别为2和1,连结DG、BE,它们之间有什么关系呢?(在实践中,我们会发现学生自己能较好地呈现这个问题)
本题三个小问由易到难,主要考察正方形的相关性质以及线段之间的关系探讨,也具有一定的开放性,发散学生的思维,让学生根据自己的理解发挥想象,再加以说理,这才是教好思考应有的行为.
当然,在不同的班级或是同一个班级不同的学生之间还是有差异的,选择适合学生的内容和方法才是最容易让学生接受的,也是学好思考的前提.其实,课堂上创新、或是有一些新的想法或见解的不一定是课堂上学习最优秀的学生,他们都有看待问题的不同角度,也就自然产生出一些与众不同的奇思妙想.
另外,通过该题的教学我们发现,正方形的旋转转出了知识的联系,也转出了问题的本质.首先由开放性问题入手,找出两条相等的线段,根据不同学生的特点会提出不同的观点和答案,再选出具有较高研究价值的答案进行研究,让学生的思维能随着问题的深入发展逐步打开,并向问题的本质靠近,不变的是什么?为什么不变?这样有利于学生思维发散后的回归.最后一问的设计,学生会根据已有经验尝试去寻找不同的关系,但是需要学生借助正方形的特点去寻找,让学生的探究欲望进一步增强,创新的思维需要进一步打开,在运动中再次寻找到线段的不变关系.这样的设计较好地拓展了学生的创新广度,有利于学生学会思考.
2.4 注重逆向补偿,引发深度思考
逆向补偿是学生“知其然、知其所以然、知其所不然”的必经途径,是深度思考、高阶投入的认知“砝码”.深入挖掘教材内涵和开发课程资源,不断大胆尝试,实践探索,积累经验和方法,分析问题时要有横纵联系,充分利用条件和结论的关系,打通最直接的联系,也许这个联系就隔着一层纸,而我们要捅破它就需要有目的地去找到问题的关键所在,从而获得解决问题的最佳途径,也增加了创新的厚度.
案例4 规律探索
为了考察正方形和一次函数的结合,我们选择了一个探究的填空题:
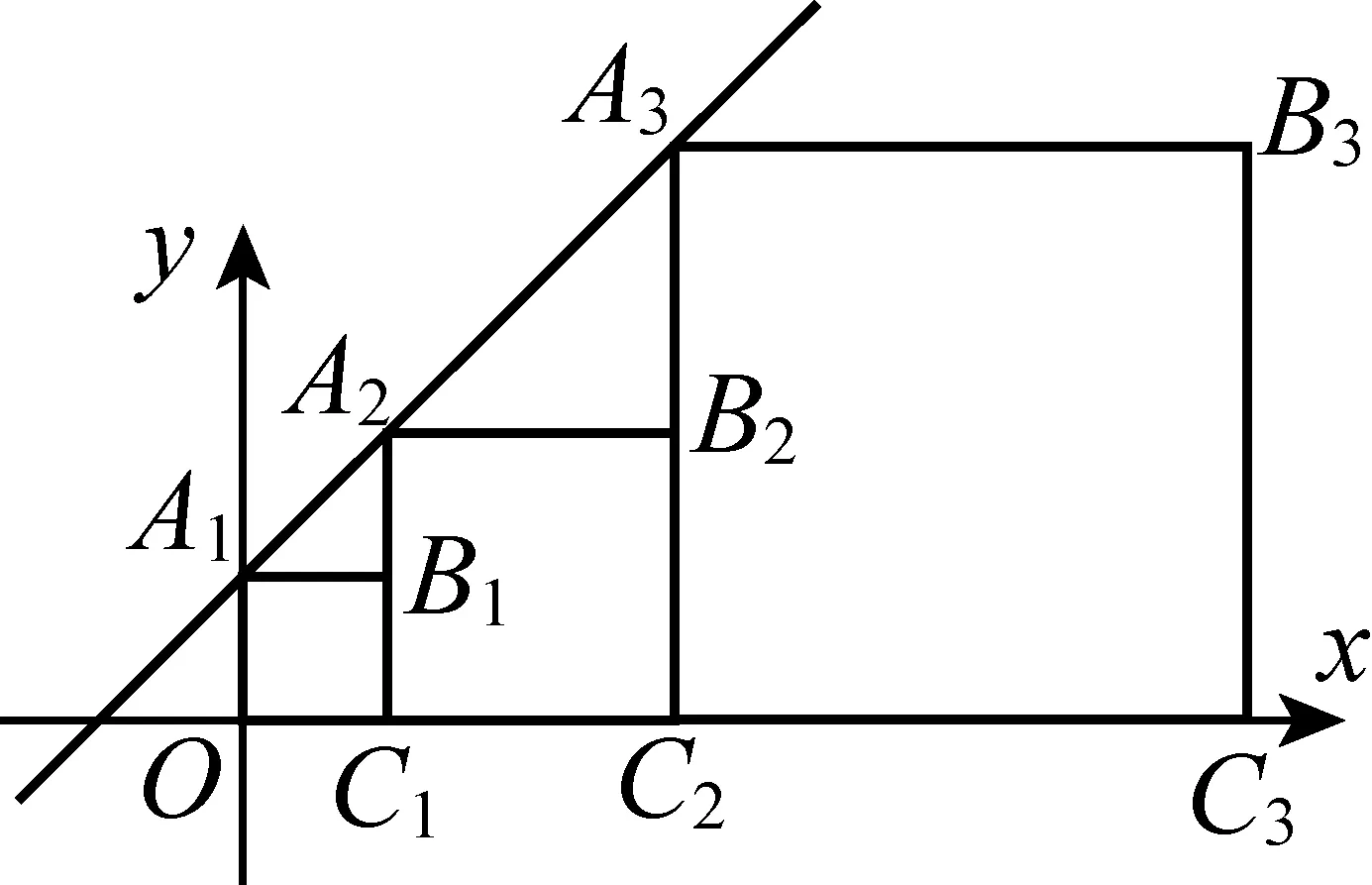
图4-1
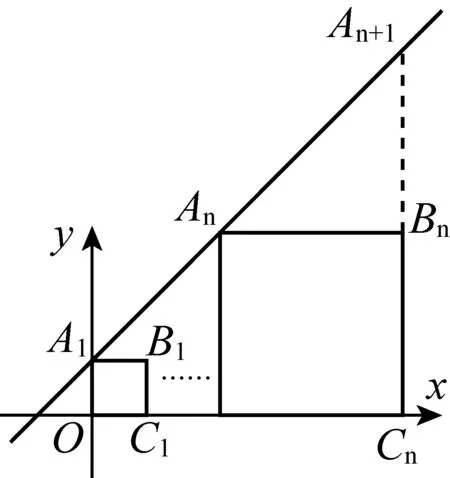
图4-2
如图4-1,在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在x轴正半轴上,依次作下去,得到如图所示的图形,则点B4的坐标是,点Bn的坐标是.
课堂教学中发现,学生很容易算出B4的坐标,但是求Bn的坐标时出现了麻烦,纵坐标能根据规律发现为2n-1,但是横坐标不知道怎么求(主要是因为找不到规律).其实,如果借助An+1与Bn的横坐标相同,借助An+1在直线y=x+1上且纵坐标为2n,就可以求出An+1的横坐标为2n-1(如图4-2),所以Bn的横坐标也为2n-1.
“教之道在于度,学之道在于悟”.“度”和“悟”是绕不开思考的.“数学是讲究方法的”,这种方法不仅仅指的是解题方法,还有思维方法,也就是为什么这样做,为什么这样想成功率会高一些,是什么条件引导我们这样想,会不会有一些其它发现或是推导出新的结论等等,所以在备课的时候要把问题备透、备足,方能适时引导学生思维向纵深发展,学生才有探究的欲望和能力,才有创新的火花产生,才有机会开花结果.本例中引导学生借助An+1与Bn的横坐标相同,解决了问题,当学生获得了解决问题的通道时,更多的是一种经验的积累.经过这样长期训练培养,他们的探究和逆向性思维就会有较好的发展.
2.5 提倡发散留白,弘扬纠错质疑
发散留白意味着给学生足够的弹性思维时空,让学生在发散思维的参与下,用好“留白”思维,实现“以一当十”的目标.当然,纠错质疑本身就是一种大尺度的发散与留白,是学生获得真知灼见和学会思考的可靠抓手.教师在课堂教学中要注重鼓励学生奇思异想,并且敢于质疑,敢于提出与自己不同的想法,这也是创新的基本要素.每一名学生都是富有个性,极具潜力的思维主体,课堂教学无疑给学生提供了一个思维空间,可以诱发学生对学习过程、方法和结果进行大胆的发问、猜想、探索和反思,教师要努力培养学生质疑的习惯,把握好时机,鼓励学生自己释疑,发展问题意识,培养探究精神,寻求解决问题的策略,促进学生思维的充分发展,从而能多维度提升学生的创新能力.
案例5 本质探究

图5
如图5中,已知抛物线y=x2-2x-3交y轴于点C,作CA∥x轴交抛物线于点A,P、R是抛物线上的动点,满足CA平分∠PCR,作OQ∥PR交抛物线于点Q,求Q点坐标.
教学片段:
师:P、R是抛物线上的动点,说明什么?
生: 说明任意位置都行啊.
师:要求Q点坐标,说明什么?
生:说明PR倾斜的程度(斜率)是不变的,才能求出固定的点Q.
生:哦,我知道了,说明无论P、R移到什么位置,PR倾斜的程度是固定的,只要求出PR这条线的k就可以了.
师:对,根据平分、相似、三角函数等知识就可以解决了.
这里需要指出的是,课堂教学中对于学生的引导和矫正要选择合适的时机,当学生遇到较难的问题时,不妨在已分析出的结论中反复推敲(留白与质疑),从中发现有价值的线索,引导学生学会思考.该题在寻找PR倾斜的程度时,需要学生仔细推敲,甚至在纠错过程中去体会PR倾斜程度是不变的,才能找到k,找到问题的解决办法.在引导过程中,学生的思维活跃程度还是非常高的,积极寻找问题的突破口,从多角度来寻找问题的答案,也较好地开辟了创新的维度.
3 结果与讨论
(1)创新中考复习,在于教思考.教思考就是要用好留白的方法,让学生“跳一跳,够得到”.教思考就是让学生在质疑中,坚持真理、修正错误,建立严谨求实的数学态度.教思考就是让学生在思维活动中培养兴趣思维,产生一种学习数学的“好胃口”.
(2)创新中考复习,在于学思考.学思考就是让问题可逆,让学生在山重水复的思考中知其然、知其所以然和知其所不然.学思考就是让学生在思维补偿中补偿思维,获得柳暗花明的思维惊喜.
(3)创新中考复习,在于教学生学会思考.教学生学会思考,就是教好换位思考,让学生建立一种从不同角度分析问题、不同层次理解问题的能力.教学生学会思考就是关注学生学习力,让学生学有所能,让学生学有所获,让不同人获得不同的数学发展.

