由一个简单不等式引发的探究

黄雅芬 李建潮

(浙江省湖州市双林中学 313012)

设x，y，z>0，则有

(y+z)(z+x)(x+y)≥8xyz

(*)

这是一个众所周知的不等式，她既不失一种天然的淳朴，又具一种纯真的优雅，从而激发了笔者探究的“冲动”，以期抛砖引玉.

1 (*)式条件的弱化

其实，使不等式(*)成立的“正数”条件可弱化为：

设实数x，y，z满足y+z>0，z+x>0，x+y>0，则有

(y+z)(z+x)(x+y)≥8xyz.

(1)

2 (1)式在代换——变式——代换中见真谛

如若在(1)式中作代换：(y+z，z+x，x+y)→(2a，2b，2c)(其中a>0，b>0，c>0)，即(x，y，z)→(b+c-a，c+a-b，a+b-c)，则有

abc≥(b+c-a)(c+a-b)(a+b-c)，

(2)

展开，可得

a3+b3+c3+3abc

≥a(b2+c2)+b(c2+a2)+c(a2+b2)

(3)

=bc(b+c)+ca(c+a)+ab(a+b).

(3′)

本文以下用∑表示循环和，∏表示循环积.

基于后续之需，不等式(3)(即(3′))还可人为地化为以下“二次”齐次不等式：

∑a3+3abc≥∑a(b2+c2)

⟺∑a3+∑a(b2+c2)+3abc

≥2∑a(b2+c2)

⟺∑a·∑a2+3abc+6abc

≥2[∑bc(b+c)+∑abc]

⟺∑a·∑a2+9abc≥2∑a·∑bc

(4)

以上(2)、(3)与(4)三式一并写为：

定理1设a，b，c>0，则有

abc≥(b+c-a)(c+a-b)(a+b-c)

(2)

(1983年瑞士数学竞赛试题)

⟺∑a3+3abc≥∑a(b2+c2)

(3)

(著名Schur′s(舒尔)不等式)

(4)

或

(4′)

进而对于△ABC，如若再对(4′)式作三角形代换：

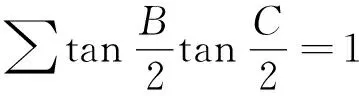
(5)

整理后发现，这竟然是如下著名不等式：

推论1(Gerrestsen不等式[1])在△ABC中，有

s2≥16Rr-5r2.

(6)

因势利导，我们再对(4′)式实施三角形代换：

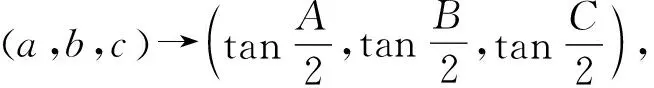
由此得：

推论2在△ABC中，有

(7)

显然，推论2的(7)式与推论1的(6)式还是蛮“吻合”的.

3 一组三角形不等式的加强

文[2]建立了如下一组三角形不等式：在△ABC中，有

(8)

(9)

(10)

(11)

其实，从定理1到推论1的过程式(5)出发可将以上这组三角形不等式加强为：

推论3在△ABC中，有

(8′)

(9′)

(10′)

(11′)

证明(5)式化为

一并用于上述不等式，可得(过渡)不等式

(12)

并注意到三角恒等式cotα-tanα=2cot2α，得

即

(8′)

并注意到三角恒等式cotα+tanα=2csc2α，得

(9′)

(10′)

(11′)

至此，加强三角形不等式组——推论3证毕.

4 Gerrestsen不等式在加强中

回首推论2的(7)式，由Euler不等式R≥2r容易知道：

这就是说，推论2的结论要弱于Gerrestsen不等式16Rr-5r2≤s2≤4R2+4Rr+3r2的“右翼”不等式s2≤4R2+4Rr+3r2，这是个遗憾.于是乎，激起了笔者向(*)式“沙里淘金”的欲望.

联想起代数恒等式：

∏(y+z)+xyz=∑x·∑yz，

(13)

而有(*)式的等价不等式：

∏(y+z)≥8xyz

(*)

(**)

并转而将等价不等式(**)的两边平方、结合平凡不等式(x′+y′+z′)2≥3(y′z′+z′x′+x′y′)(其中x′，y′，z′为实数)，可知(*)式的又一强化：

与前相仿，使这一强化不等式成立的“正数”条件(明显)可弱化为：

设实数x，y，z满足y+z>0，z+x>0，

x+y>0，则有

(14)

使之成为不等式(1)的(一个)强化不等式.于是，理所当然地用仿照获取定理1的代换或方法将定理1强化为：

定理2设a，b，c>0，则有

27a2b2c2≥(∑a)3·∏(b+c-a)

(15)

(16)

(17)

或

(17′)

接下来，先在△ABC中，依然仿前对(17′)式作三角形代换：

(18)

(19)

次对(17)式作如下放缩处理.

利用不等式(2∑a)3=[∑(b+c)]3≥33∏(b+c)，将(17)式中的相关部分放缩为

故而由(17)(即(17′))式，再获得：

推论4设a，b，c>0，则有

(20)

或

(20′)

推论5在△ABC中，有

(21)

或

(21′)

其中的(21)式即为著名的Garfunkel-Bankoff(见文[3])不等式.

结合Euler不等式R≥2r，便知(21′)(即(21))式Garfunkel-Bankoff不等式是Gerrestsen不等式s2≤4R2+4Rr+3r2的三角形形式的加强.

至此，有机联立(19)与(22)二式，便是Gerrestsen不等式16Rr-5r2≤s2≤4R2+4Rr+3r2的加强：

推论6在△ABC中，有

(23)

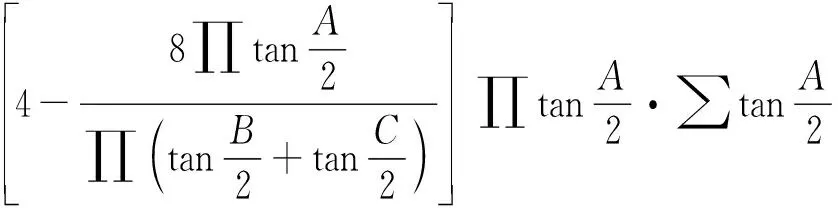
即

推论7在△ABC中，有

(24)

(24′)