基于实车数据的电动汽车电池健康状态预测*

胡 杰，朱雪玲，何 陈，杨光宇

（1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉430070；2.武汉理工大学，汽车零部件技术湖北省协同创新中心，武汉430070；3.新能源与智能网联车湖北工程技术研究中心，武汉430070）

前言

电动汽车是现代汽车发展的主要方向，其动力电池组健康状态（state of health，SOH）是对当前电池性能的综合评估，可直观体现电池寿命变动［1］。因此，电动汽车动力电池SOH的准确预测是保证车辆可靠与安全的前提，具有十分重要的现实意义。目前，电池SOH预测方法大体可分3类：模型法、数据驱动法和融合法［1］。基于模型的电池SOH预测方法主要包括电化学模型法、经验模型法和等效电路模型法，电化学模型法可了解电池内部状态，预测精度较高，但无法确定电池内部衰减机理且设备昂贵［1-3］；经验模型法建模难度低，但模型稳定性差［1-3］；等效电路模型法可实现电池SOH的实时预测，但模型参数识别误差存在累积现象，预测精度受模型结构影响较大［1-3］。相较于模型法，数据驱动法无须考虑电池内部的复杂反应与老化机理，可利用电池状态参数建立模型［1-4］。融合法是指将模型法与数据驱动法相混合，可明确模型参数，预测精度较高，但计算复杂且依赖于试验数据［4］。

基于数据驱动的电动汽车电池SOH的估计多基于电流、电压、容量和内阻等参数；王常虹等［5］在试验数据基础上提出了可反映电池SOH情况的容量衰退参数，实现电池剩余寿命的准确预测；Yu［6］通过拟合电池容量的全局退化趋势实现电池SOH的准确预测；刘中财等［7］归一化处理电池实验测得的内阻值，利用内阻值表征电池SOH；梁培维等［8］分析不同放电倍率下电池内阻的变化特性，选用三次样条插值法实现电池SOH准确预测；Jun等［9］采用小波分解处理电池电压，提出了基于小波分解的电池SOH预测方法；徐文静［10］在单体电池充放电循环试验中测到多种条件下的电池充电电压曲线，建立充电电压归一化拟合模型去预测电池SOH；Chang等［11］在实验基础上考虑电池内阻与放电瞬时压降对电池SOH的影响，建立BP神经网络预测电池SOH；郝雪玲［12］在实验数据下分析构建电池SOH综合指标，选择容量、内阻和恒流充电时间3项指标用于电池SOH预测上。综上，现有基于数据驱动的电池SOH预测较少采用多指标融合预测，且大多基于试验数据，未能考虑实车运行的复杂情况。

本文中以电动汽车实车运行数据分析电池SOH预测问题，选择构建容量、内阻和电池一致性3项指标，建立LightGBM模型，采用5-fold交叉验证计算各项误差，实现基于实车数据的电池SOH准确预测。针对实车数据存在的问题，提出自适应状态估计法实现在不完整状态下的容量计算，并考虑多目标优化问题，利用NSGA-II算法确定电压区间，提高估计精度；考虑单体电池差异对电池整体寿命的影响，选择单体温度极差与电压极差表征电池的温度一致性与电压一致性，构建电池一致性评分标准。

1 数据与分析

1.1 样本数据

本文中使用的数据为京、沪两地各5辆在运行电动营运车辆的实际行驶数据，时间为2018年至2020年，车辆日常数据是通过车载数据记录仪进行采集，数据采样周期为10 s，获得数据集样本总量为7 543万，该样本量可以确保本次采集数据具有一定的广泛性和代表性，数据信息如表1所示。

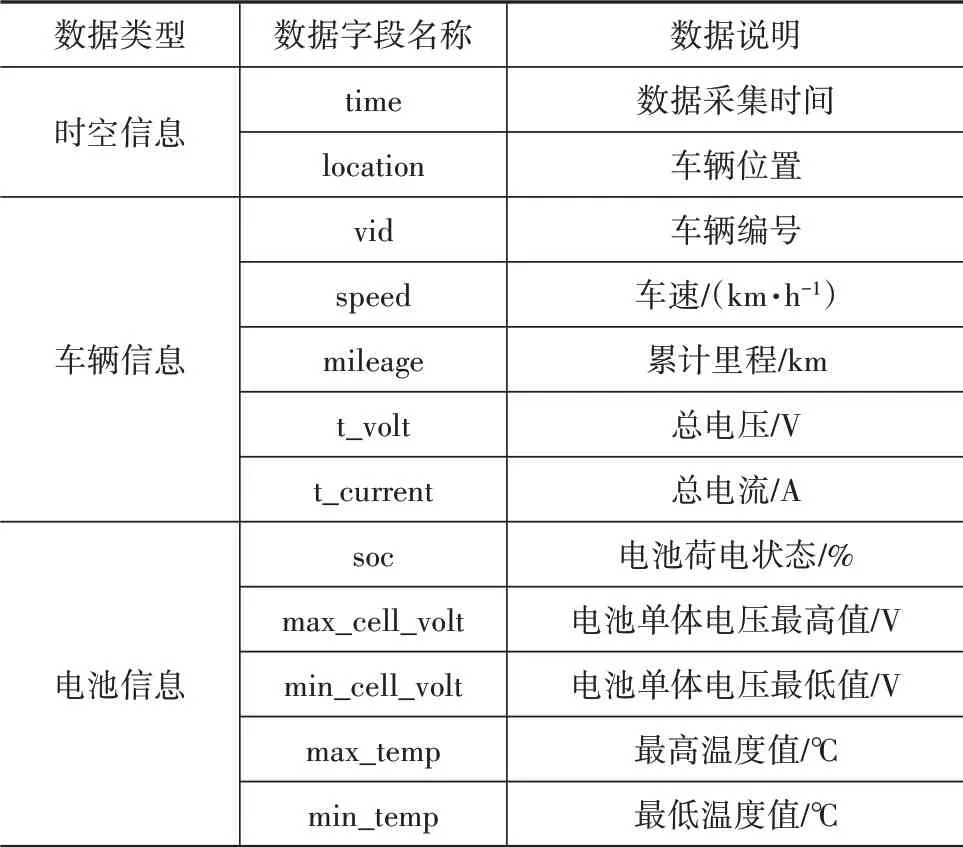
表1 数据分类与说明

1.2 问题分析

电池SOH是指电池当前性能状态与原始性能状态之比，表征电池健康程度［12］。将实车数据按编号进行预处理，清洗后划分充放电片段进行SOH相关性分析，并随机抽取1∕4的片段作为测试集。构建容量、内阻和一致性评分标准，选择LightGBM模型进行电池SOH预测，并用测试集进行验证，流程如图1所示。

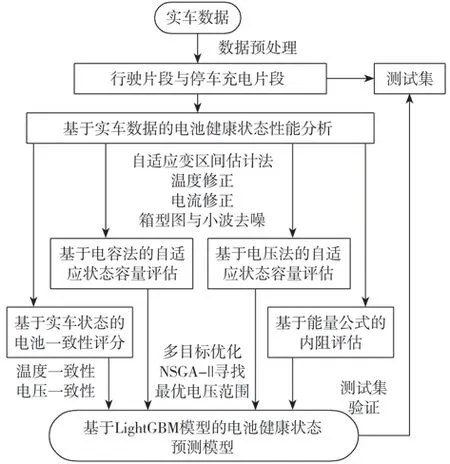
图1 多指标预测电池SOH流程框图

2 数据预处理

车载传感器采集车辆行驶数据，其信号受多种因素影响，可能会出现信号不稳定等现象，造成部分数据呈现异常，因此需对异常数据进行处理，表2为部分异常的原始数据。

表2 部分异常数据

2.1 片段划分

为了便于后续异常数据处理和SOH预测，选择先对原始数据进行基于车辆状态、时间维度和空间维度的片段划分，片段划分目标为行驶片段、停车充电片段和静置片段，划分流程如图2所示。

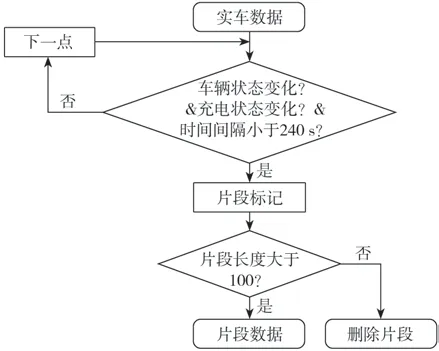
图2 实车数据片段划分流程图

2.2 异常数据处理

本文中的数据异常类型主要包括采集滞后数据、状态标记异常数据和缺失数据。采集滞后数据和状态标记异常数据可通过其余特征来进行状态平移或修正；缺失数据主要在里程、速度、最高最低单体电压和最高温度数据中，里程与速度缺失值选择以片段为单位进行片段内填充，最高最低单体电压和最高温度的缺失值则通过机器学习模型随机森林进行填补，该方法经过5-fold交叉验证计算平均相对误差如表3所示。

表3 随机森林填补误差

随机森林是Bagging与决策树结合的集成学习方法，可用于解决分类、回归等问题。训练样本集合为S，经过随机向量θk随机化得到k个训练样本，训练样本和随机向量生成每棵决策树，决策树的集合即为随机森林h(S，θ)={h(Sk，θk)，k=1，2，...，K}，每棵决策树模型都有一票投票权决定输入变量di的输出结果，再对每棵决策树产生的结果H(di)=

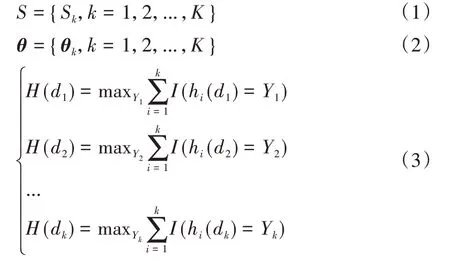
式中：H(x)为随机森林输出结果；hi(x)为单个决策树输出结果；Y={Yk，k=1，2，...，K}为目标；I(x)为示性函数。

2.3 电池SOH相关性分析

电池SOH随着充放电循环次数的增多而衰减，二者之间相关性较强，经数据探索发现，充放电循环次数对电池的影响主要体现在充放电的荷电状态（SOC）变化与充电电压变化上。

2.3.1 充电过程的电压变化电池在快充和慢充的情况下充电电流有明显的差别，因此本文中分别明确定义了快充和慢充两种模式。通过对数据的进一步探索发现，在两种模式下充电电压变化曲线都呈现以下趋势：随着循环充放电次数的增加，电压变化越陡峭，即充电时间缩短，充入电量减少。

2.3.2 充放电SOC变化

图3为不同循环周期充放电SOC变化曲线，可见无论在何种模式下电池循环充电次数越高，充电达到同样SOC所耗时间越少。

图3 不同循环周期充放电SOC变化曲线

出现上述现象的原因是随着电池循环充放电次数的增加，电池内阻和电容会存在不同程度的增加或减少，电池的温度一致性和电压一致性也会变差。

3 特征工程

3.1 容量

电池容量是当前研究电池SOH中使用最多的特征，其值随着电池循环放电次数的增加而降低，可体现电池SOH的整体衰减趋势。本文中采用安时积分法计算当前容量值，计算方法［14］如下：

式中：CM为当前容量值；I为当前片段内的电流；ΔSOC为当前片段内的SOC差。

3.1.1 自适应状态估计法

传统容量估算法是采用当前电池最大容量和新电池最大容量的比值来计算电池SOH，电容法需要测算出电池SOC值从100%放电至0的放电量，电压法须测算出电池电压在固定变化区间内的充电量。可见，传统容量估算法须获得较为完整的充放电区间，要求电池进行完全的充放电，故传统计算方法仅适合实验室条件下完整充放电数据。

实车行驶状况复杂多变，难以获得完整的充放电区间，本文中针对传统方法进行改进，提出自适应状态的电池容量估算方法，该方法可有效解决实车数据区间不完整所带来的问题，实现自适应状态的电池容量估计。自适应状态估计法选取较为完整的电压片段作为标准片段，其余片段动态截取相同电压与相同电压降的对应区间，计算电容的比值进行SOH评估，并考虑快充和慢充的差异，分别对二者进行该过程，图4为实车SOC分布，图5为自适应变区间容量估计示意图，图中每条曲线表示该时间段电池充放电电压变化情况。

图4 实车SOC分布

图5 自适应状态估计法

3.1.2 容量值的修正

研究表明传统的安时积分法计算容量存在误差，温度与放电电流在一定程度上影响着电池容量值，二者主要通过影响电池内部的化学反应，使电池容量快速衰减［14］，本文中选择依照温度与放电电流对电池容量计算值进行修正。

温度对容量值的修正依据文献［15］中提出的修正公式，具体如下所示：

式中：C1(t)为温度修正系数；e为自然指数；t为平均温度，其计算如式（6）所示；Tmin为片段中单体最低温度的平均值；Tmax为片段中单体最高温度的平均值；Ci为未经修正的电池容量值；C(t)为经过温度修正的容量值。

放电电流对容量的修正参照文献［15］中修正的流程，通过拟合曲线得到放电电流的修正系数公式，再将电池容量修正到标准电流下，修正公式如下：

式中：C2(i)为修正系数；i为每个放电片段的平均放电电流；Ci为未经电流修正的电池容量值；C1(i)为经过电流修正后的电池容量值。

3.1.3 容量离群点处理与去噪

修正后的容量值仍存在部分样本点远离数据中心，该部分即为离群点，其产生主要是受传输过程中不稳定因素的影响，如当天气候、采集设备状态等，为提高电池SOH预测模型的精度，本文中采用箱型图去除容量离群点，离群点指处于箱形图上下边缘之外的点，处理结果如图6所示。

图6 箱型图

数据获取过程中的随机误差或者环境影响都可能使数据产生噪声，影响整体的均衡性，增加后续建模的难度。鉴于小波变换保留了特征提取的部分，性能上优于传统的去噪方法，故本文中采用小波去噪的方法对容量值进行去噪处理。

3.2 内阻

电池内阻是影响电池SOH的重要因素之一，研究表明动力电池组内单体电池SOH与电池欧姆内阻之间有一定联系，与极化内阻无明显关联［16］。受温度、充放电电流等因素的影响，内阻值处于动态变化的状态，这种变化可从侧面表征电池SOH。一般，充放电循环次数越大，内阻值越大，关系如图7所示，本文中通过一次循环内的充放电能量公式求出使用状态下的电阻，公式如下。

图7 内阻与充放电循环次数关系图

式中：I1、I2分别为充电电流与放电电流；E为行车消耗的能量；RNOW为当前的内阻值。

3.3 电池一致性

电池组整体充放电时，环境与自身性能的差异使得各单体电池电流、放电深度和端电压多有不同，各单体电池性能衰减程度不一，可能会导致电池组提前失效［17］。为多尺度预测电池SOH，本文中进行了电池一致性评价，受数据维度的限制，本文中仅分析电池组的温度一致性与电压一致性，综合样本数据特征，选择使用单体温度极差与单体电压极差表征电池的温度一致性与电压一致性。

评价单体电池温度一致性的公式如下：

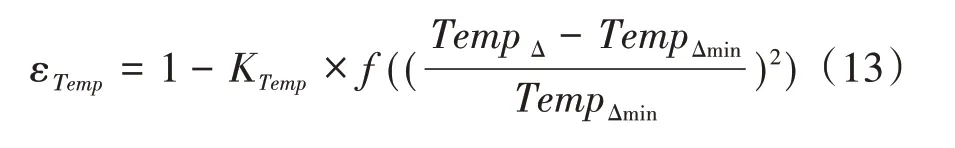
评价单体电压一致性的公式如下：

式中：Tempmax、Tempmin和Umax、Umin分别为该时刻数据中单体温度最大值与最小值和单体电压最大值与最小值；TempΔmin、UΔmin为该车历史数据中单体温度极差与单体电压极差的最小值；f为归一化函数为一 致性得分修正系数；εTemp、εu为最终的温度一致性与电压一致性得分。

本文中取KTemp与Ku为0.2，并计算最终的温度一致性与电压一致性得分，电压极差与温度极差分布Q-Q图如图8和图9所示，其中μ、σ、skew、kurtosis分别代表数据分布的均值、方差、峰度和偏度，两条分布曲线分别代表样本实际分布与拟合标准正态分布。图10为一致性得分，其中1为满分。

图8 电压极差分布图

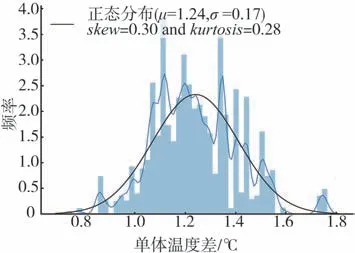
图9 温度极差分布图

图10 温度一致性和电压一致性得分

4 模型构建与验证

4.1 电池SOH计算

基于电容法定义的电池SOH［15］为

式中：CM为当前容量；CN为初始容量。

基于电压法定义的电池SOH［18］为

式中：CNOW(U1-U2)为电压从U1降低到U2消耗的电量；CNEW(U1-U2)为新电池电压由U1降低到U2消耗的电量。

基于内阻法定义的电池SOH［16］为

式中：RNEW为新电池，也即SOH为100%时的内阻值；RNOW为当前，也即电池在使用过程中测量的内阻值，本文中采用充放电能量公式（式（10）和式（11））对一次循环内的RNOW进行计算；REOL为电池寿命终了时的内阻值，一般取SOH为80%时的内阻值。本文中先构建基于自适应状态估计法的容量法预测模型，并对前10个充电循环对应的电池健康状态进行评分，结合能量公式计算该状态下的内阻值。

基于电容法、电压法、内阻法构建的电池SOH评估结果分别如图11～图13所示。

图11 电容法

图13 内阻法

4.2 多目标优化

自适应状态估计法可有效针对实车数据不连续问题实现变区间容量值估计，其电压片段的选择是保证其估计精度的关键，本文中考虑基于最优部分充电电压分布中估算电池容量。

图12 电压法

若选用单一电压片段作为参考片段，可采用网格搜索法进行选择，网格搜索是一种通过交叉所有候选解来优化代价函数的全局搜索方法，故采用该方法可找到一个最优电压范围，保证容量的估计精度，但该方法只优化估计精度，不考虑电压范围长度，且实际生活中充放电电压区间不一定都能通过该范围。本文中综合考虑精度与效率的多目标优化问题，采用非支配排序遗传算法（NSGA-II）自动选择多个最优电压范围，找到最佳的折中方案。

NSGA-II能够有效地找到多目标优化问题的Pareto最优，它使用一种带有精英策略的快速非支配排序方法，降低计算复杂度，大幅提升排序速度，保留最优解，保证了个体多样性。本文中采用图14所示流程寻找两个最优电压范围，采集电池退化过程中的充电电压曲线，形成原始数据集，NSGA-II创建最初的亲本种群，利用NSGA-II的代价函数来评估种群中每个个体的适应度，采用快速支配排序算法为每个个体分配一个非支配层，同时给出同一层中个体的拥挤距离，NSGA-II再从最优非支配集中选择新种群，对同一非支配层个体利用拥挤距离进行评估，遗传操作包括选择、交叉和突变，主要用于从新种群中产生后代，满足条件后停止。

图14 NSGA-II选择电压范围流程

NSGA-II中的双电压范围的染色体状结构如图15所示，图中的4个电压值(Ua1，Ua2，Ub1，Ub2)构成了每个个体的结构，Ua1和Ua2与Ub1和Ub2分别为两段电压范围的起始点和结束点，其中Ua1＜Ua2，Ub1＜Ub2。每个个体的适应度由NSGA-II的代价函数进行评价，考虑所提方法是为实现准确估算电池电容值并提高效率，提升SOH预测精度，故代价函数分别设计为容量估算误差f1、电压片段平均长度f2，代价函数f1与f2的值均为越小越好，具体公式如下：

图15 类染色体状结构

式中：Ci为计算容量；为参考容量；LUa1-Ua2、LUb1-Ub2分别为电压Ua1与Ua2、Ub1与Ub2之间的平均长度值。

利用NSGA-II算法确定自适应状态估计法中用于计算容量的电压范围，即图5中选择的电压范围，图16为NSGA-II电压片段选择结果。

图16 NSGA-II电压选择结果

综上所述，多目标优化问题是效率与精度两个目标的冲突问题，NSGA-II是解决多目标优化问题的算法，利用该算法可找到精度与效率的最优点，完成对自适应状态估计法中电压片段的选择，提升容量的计算精度，考虑多目标优化问题的自适应状态估计法计算流程如图17所示。

图17 考虑多目标优化问题的自适应状态估计法计算流程

4.3 电池SOH模型构建

LightGBM算法是微软的开源GBDT（gradient boosting decision tree）算法，该算法引入单边梯度采样算法和互斥特征捆绑算法，可减少计算量，提高效率，可有效打破传统GBDT算法的局限性。

K折交叉验证（K-fold cross validation）是指将样本集分割成K份，取一份作为验证集，其他K-1份作为训练集，重复训练K次，取K次结果的平均值作为最终误差，可提高模型的泛化能力，图18为5折交叉验证示意图。

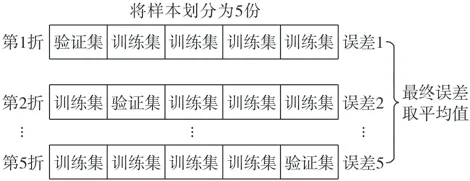
图18 5折交叉验证示意图

依据电压片段的选择是否考虑多目标优化问题分别构建前文所述特征，建立LightGBM模型，图19为电池SOH两种多指标预测与实际拟合的对比图。采用5-fold交叉验证计算各项误差，其分布分别如图20～图22所示。表4对比了不同方案预测电池SOH的误差，结果表明基于多目标优化的多指标融合预测方案可明显提高电池SOH预测准确性。

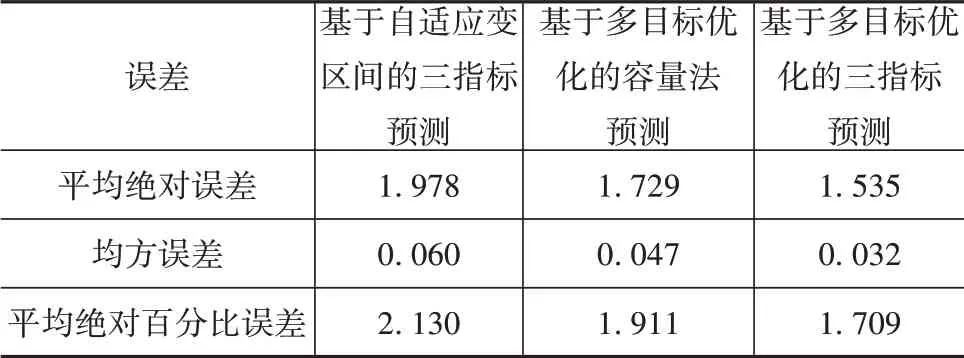
表4 各方案预测误差 %

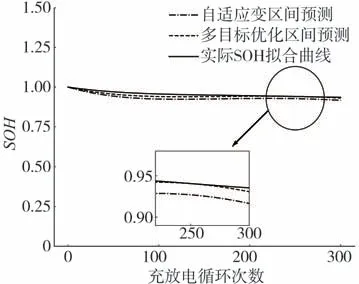
图19 电池SOH多指标预测对比图

图20 测试集绝对误差图

图22 测试集平均绝对百分比误差图

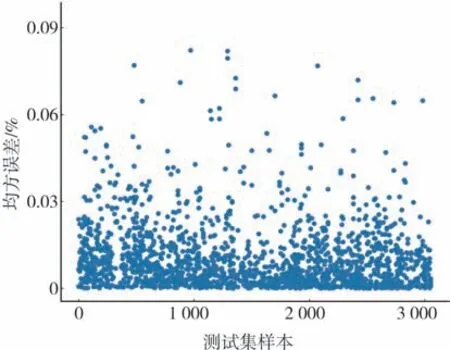
图21 测试集均方误差图

5 结论

针对实车数据存在的问题，本文中将数据区间特征考虑到容量估计中，利用自适应状态估计法计算当前容量值，并考虑单一电压片段的局限性，利用NSGA-II算法解决精度与效率的多目标优化问题，在该算法中利用容量估算误差和电压片段长度确定个体适应度，最终选择2个最优电压范围，有效提高变区间电池容量估计精度。以容量、内阻与电池一致性评分标准为3项指标，并结合LightGBM算法构建电池SOH预测模型，结果表明采用多目标优化的三指标融合预测方案的各项误差均为最低，其中平均绝对误差为1.535%，较未采用时降低了0.443个百分点，较采用后的单指标降低了0.194个百分点，即本文中提出的方案能有效处理情况复杂的实车数据，显著提高基于实车数据的电池SOH预测精度。