同构并非唯一法 问题破解有良方——对2020年新高考山东卷第21题的另解与思考

何 灯 周 宁

(1.福建省福清第三中学 350315;2.福建师范大学附属福清德旺中学 350319)

山东省作为新高考综合改革的先行省份，其命制的第一份新高考数学试卷引起社会广泛关注.其中，吸引笔者更多目光的是该卷的导数压轴题.

一、试题再现与解析

题目已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

分析试题第(2)问以学生熟悉的恒成立条件下求参数范围问题呈现，乍看平淡无奇，朴实无华，细细品味后却感觉内涵丰富，给人启迪．

对于含参函数试题，求解的通法是参数分离法或求导法.但该题包含了以e为底的指数函数和对数函数，因指数对数相互纠缠，运用参数分离法求解无法分离出参数，运用导数法求解无法求出极值点，进一步处理困难.此类问题利用同构法往往能够轻松破解.

所谓同构法，就是通过对不等式恒等变形，将其转化为形如F(g(x))≥F(h(x))(或F(g(x))>F(h(x)))的结构，利用导数研究F(x)的单调性进行求解.此法不但展现了数学的对称和谐美，更是把转化与化归思想体现得淋漓尽致.

下面是文[1]中利用同构法给出试题第(2)问的一个解答.

解析1 由题意f(x)≥1恒成立等价于elna+x-1+lna+x-1≥x+lnx恒成立，等价于elna+x-1+lna+x-1≥elnx+lnx恒成立.令F(x)=ex+x，则F′(x)=ex+1>0，F(x)关于x在(-∞,+∞)上单调递增，从而elna+x-1+lna+x-1≥elnx+lnx恒成立等价于F(lna+x-1)≥F(lnx)恒成立，等价于lna+x-1≥lnx恒成立，即lna≥lnx-x+1恒成立.

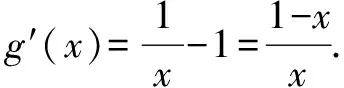
故lna≥0，a≥1，所求a的取值范围为[1,+∞).

思考(1)上述解法构思巧妙，学生前期如果没有经过训练，无法完成aex-1-lnx+lna≥1到elna+x-1+lna+x-1≥elnx+lnx的转化，更难想到构造函数F(x)=ex+x以简化问题求解过程；(2)求解本题，常规的参数分离法和求导法均较难奏效，那么同构法是否是求解本题的唯一方法？

针对上述思考，笔者对问题的求解展开了探究.事实上，处理含参问题还可以借助图象的直观特性来辅助思考，通过对aex-1-lnx+lna≥1形式的分析，笔者得到如下解法.

上述解法的巧妙之处在于充分利用了表达式的结构特点和函数图象的特征，展现了化归转化思想和数形结合思想在解题中的引领作用，彰显了试题的本质.

那么，上述方法何时适用？在使用中应注意哪些问题？

二、方法提炼

适用情况(1)参数居于两个位置，如aex-1-lnx+lna≥1中参数a居于ex-1的系数位置及lna的真数位置；

(2)表达式中同时含有同底的指数函数及对数函数；

(3)将原不等式等价变形为y1(x)≥y2(x)(或y1(x)>y2(x))的形式，且y1(x),y2(x)互为反函数.

使用步骤(1)将表达式等价变形为y1(x)≥y2(x)(或y1(x)>y2(x))的形式；

(2)由于y1(x),y2(x)互为反函数，二者图象关于y=x对称，y1(x)≥y2(x)(或y1(x)>y2(x))恒成立等价转化为y1(x)≥x(或y1(x)>x)恒成立；

(3)针对y1(x)≥x(或y1(x)>x)恒成立，采用参数分离法或求导法求解，得出参数的取值范围.

三、方法应用

例1 (2019年武汉调研，2020年安徽六安一中模考)已知函数f(x)=ex-aln(ax-a)+a(a>0)，若关于x的不等式f(x)>0恒成立，则实数a的取值范围为( ).

A.(0,e]B.(0,e2) C.[1,e2] D.(1,e2)

所以a的取值范围为(0,e2)，选择B.

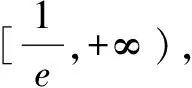
四、解题教学感悟

知识是载体，方法是手段，思想是灵魂，它们是知识体系的三个层次.碰到难题，我们应站在思想的高度来思考和引领方法，这样才能从“山重水复疑无路”的窘迫中解脱，感受到“柳暗花明又一村”的欣喜.