探析初中数学几何例题的讲解方法
汤裕斌
(永嘉县巽宅镇中学,浙江永嘉,325117)
摘 要:针对学生解决几何证明题比较困难的情况,给学生分析研究几何证明题的解题方法与技巧,提高学生学习几何的兴趣,增强解决问题的信心。
关键词:几何例题 讲解方法 循序渐进 分离法
面對许多复杂的几何题目,有时常常让人束手无策,找不到解决问题的突破口,如何打破这一尴尬,走出这一窘境?
在初中数学课堂中,教师离不开例题的讲解,例题讲解方法多样。下面,笔者结合多年的教学经验和方法谈谈几何例题的讲解方法。
一、循序渐进法
一个例题的直接呈现,对于部分同学的解题来说有一定的难度,但是通过“循序渐进法”,可以让每个学生动手把每一步骤的图形补充起来,让学生真正的参与到解题中,更有效的解决大题,难题以及原本他不会的题。
案例1:
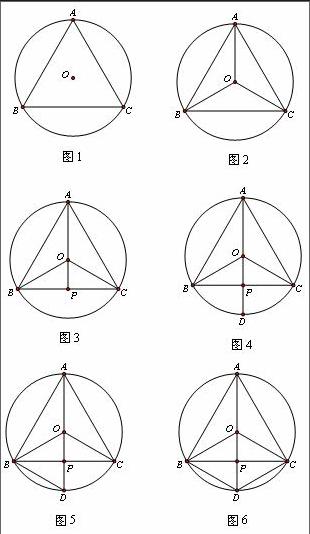
步骤1:如图1,等边三角形ABC内接于⊙O。
步骤2:连结OA,OB,OC,请问从图2中你可以得出哪些结论?从边、角度的方向来考虑。
结论:∠AOB =∠COB=∠AOC=120度;
∠BAO=∠CAO=∠ABO=∠CBO=∠ACO=∠BCO=30度。
步骤3:延长AO,交BC于点P,请问从图3中你可以得出哪些结论?
结论:AP垂直BC,∠BOP=∠COP=60度,BP=PC。
步骤4:延长AO,交弧BC于点D,请问从图4中你可以得出哪些结论?
结论:DP=PO。
步骤5:连结BD,请问从图5中你可以得出哪些结论?
结论:△BOD是等边三角形
步骤6:连结DC,请问从图6中你可以得出哪些结论?
结论:四边形BDCO是菱形。
二、分离基本图形法
所谓“分离法”,就是指在复杂的图形中将简单的基本的几何图形从中“分离”出来,以便运用简单基本图形的性质,得出重要的中间结论,然后又将这些中间结论作为新的已知,去解决整个问题。
案例2:
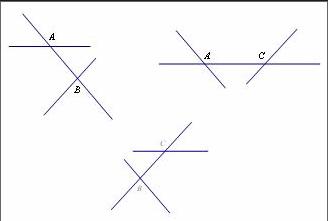
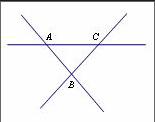
如图,AB与AC交于点A,AB与BC交于点B,AC与BC交于点C。图中有几对同位角?几对内错角?几对同旁内角?
学生们如果直接在图中找,会比较复杂。如果选择“分离基本图形法”分离出三个“三线八角”,再去数的话就会更加简单、明了。
“三线八角”是常用的一个基本图形,同时还有“三垂足一线”、“角平分线+平行线”等基本图形。
几何的学习主要在于培养空间抽象能力的基础上,发展学生的逻辑思维能力和空间想象能力。
数学教学中,开启教学智慧,创造性实施教学,在几何教学中巧妙运用讲解方法,让其助推学生几何思维和空间观念的发展。

