平面解析几何的综合问题求解方法分析

周福云

(江苏省南通中学 226001)

一、平面解析几何与向量之间的综合问题

在平面解析几何中，所涉及的直线、圆、椭圆、双曲线以及抛物线方程都是建立在二元正交坐标系中，这为向量的应用提供了良好的基础.因此，在平面几何中，平移、全等、相似以及夹角都能够通过向量的线性运算以及数量积的运算进行表示.所以，在教学中，教师们需要让学生们通过大量例题的练习，寻找到向量与平面几何之间的关系，进而运用向量，有效求解有关平面解析几何的题目.在平面解析几何中，有一些题目会涉及到角度，所以，教师们就可以引导学生们从数量积入手.在例1的求解中，就可以通过把钝角化解成向量的数量积的问题，从而很好地解决例1.

所以点p(3cosA，2sinA).

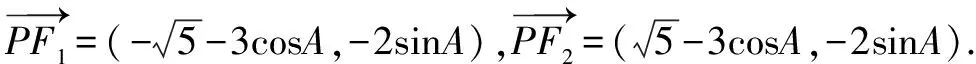
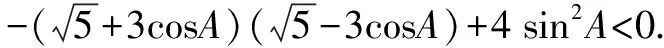
总之，在高中数学中，向量是解决问题的一个工具或载体.在高考试卷中，对于向量解决的有关解析几何问题有以下几个方面:①运用向量线性计算的基本概念与基本知识，如向量共线、垂直等问题；②求动点的轨迹方程以及直线与圆锥曲线之间的关系时会运用到向量；③以向量的基本运算为切入点以及曲线的有关定义进行解决.

二、平面解析几何与数列之间的综合问题

在数学高考中，经常会出现解析几何与数列的交汇问题，并且，这类题型经常以压轴题的形式出现.所以，明确解析几何与数列之间的关系问题是高中数学学习的重点与难点，教师们需要让学生们在课堂学习中熟悉数列的基本概念和性质，并通过不断地练习，探索出数列与解析几何之间存在的内在关系，进而使得学生们能够在考试时运用摸索出的关系进行有效答题.在例2的证明中，需要运用到两个知识点，也就是说，学生们要熟练地将等比数列的基本性质与抛物线的基本性质进行有效结合，从而将知识点进行融会贯通，达到解决题目的目的.

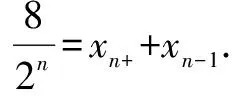
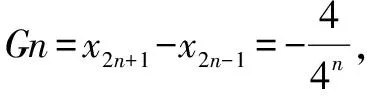
当然,此题还有第二种证明的方法，那就是归纳法，使用归纳法证明时计算比较繁琐，所以笔者在这里就不做过多的阐述.教师们可以引导学生们在课堂中或者是课后运用归纳法进行解题，使之与文章中的解题方法进行比较.

综上所述，解析几何是高考数学中的重要分支，除了上述两种解题技巧外，数学教师们还应当带领学生注重解析几何中的最值与定值定点的问题，其次，教师们也应当让学生们了解解析几何与导数之间的交汇，从而使得学生们能够在有关平面解析几何的题目中有一定的解题策略.