电磁轨道炮电枢前感应磁场特性及其受力分析

李天亮，殷大虎，陈烺中，乔朋朋

(中国人民解放军93221部队，北京 100085)

0 引言

电磁轨道炮结构简单，弹丸能量巨大，且针对不同目标可调节发射电流进行弹丸能量定制，在空天防御等领域军事潜力巨大。电枢作为轨道炮中核心运动部件，也是将系统的电磁能转化为动能的媒介，研究其受力特性对于优化系统结构、提高轨道炮系统能量效率等方面具有决定性作用[1-3]。

电枢前的电磁场特性是决定其受力的根本因素，本文在忽略轨道电阻、电流趋肤效应等因素基础上，基于面电流假设，建立了轨道内电磁感应强度计算模型，研究轨道通流后在电枢前形成的电磁场特性，以及轨道通流长度对磁感应强度、轨道电感梯度、电枢受力的影响。

1 电磁轨道发射器物理模型

电磁轨道炮从系统结构和物理原理角度可视为一台直线电机，结构上包括一对平行金属轨道、可在轨道间滑动的电枢、为电磁轨道炮系统提供能量的大功率脉冲电源，以及联接线缆和开关等辅助设备[4-7]，其结构如图1所示。

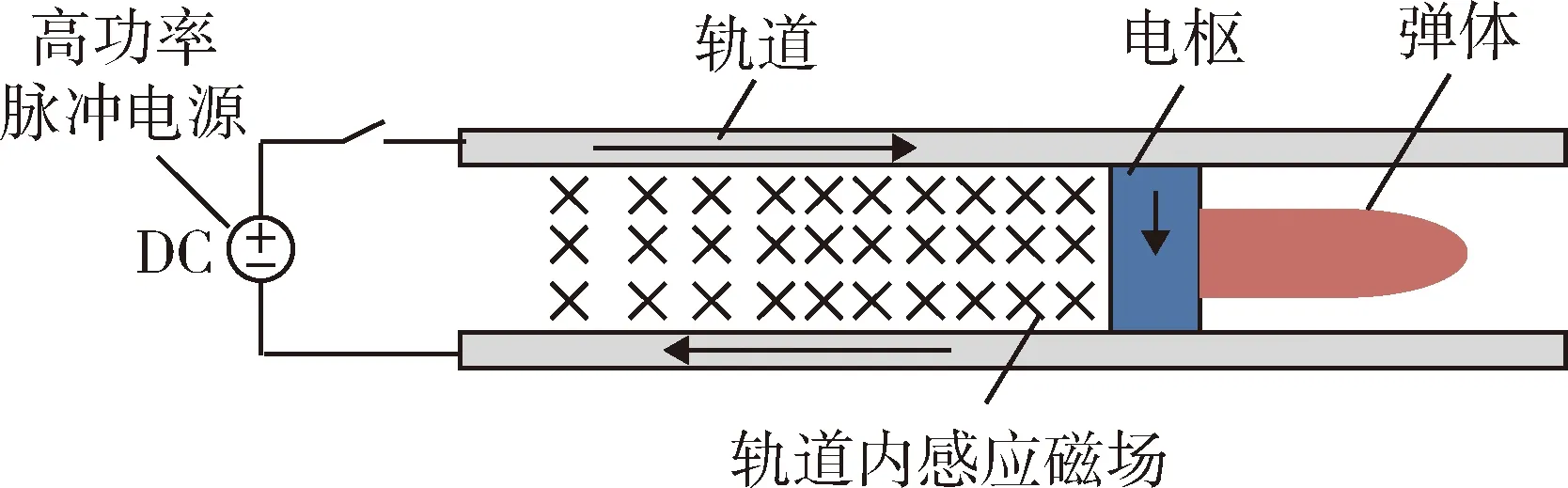
图1 电磁轨道炮结构示意图Fig.1 Illustration of railgun structure

轨道炮的工作原理相对简单，当电源开关接通后，由金属导轨、电枢、电源构成的电路闭合，脉冲大电流流过电路，并在轨道内形成感应电磁场，电枢在其所受到安培力、摩擦力等外力综合作用下，开始加速运动，直至飞出轨道。

电枢是轨道炮的核心器件，也是系统中唯一的运动部件。一方面要导流脉冲大电流，形成电流闭环，另一面还要在和轨道保持良好电接触条件下进行高速滑动，同时还要支撑弹体，保持内弹道的稳定性。电枢安装于轨道之间，由电导体材料制成，从结构形态上可分为3种类型，固态金属、等离子体、复合形态。由于电枢在运动过程中要须与轨道良好接触，电枢与导轨之间必须有预紧力，在高速运动情况下(大于3 km/s)通常采用等离子体电枢，而速度较低时(3 km/s以下)通常采用固体电枢。

从电路结构视角看，电磁轨道炮可视为由电源驱动的电负载[6-8]。由于电枢沿着轨道运动，系统总电阻和总电感会随着电枢运动距离增加而增加。如此，轨道的阻抗特性可等效为可变电感Lr(x)和可变电阻Rr(x)，如图2所示。

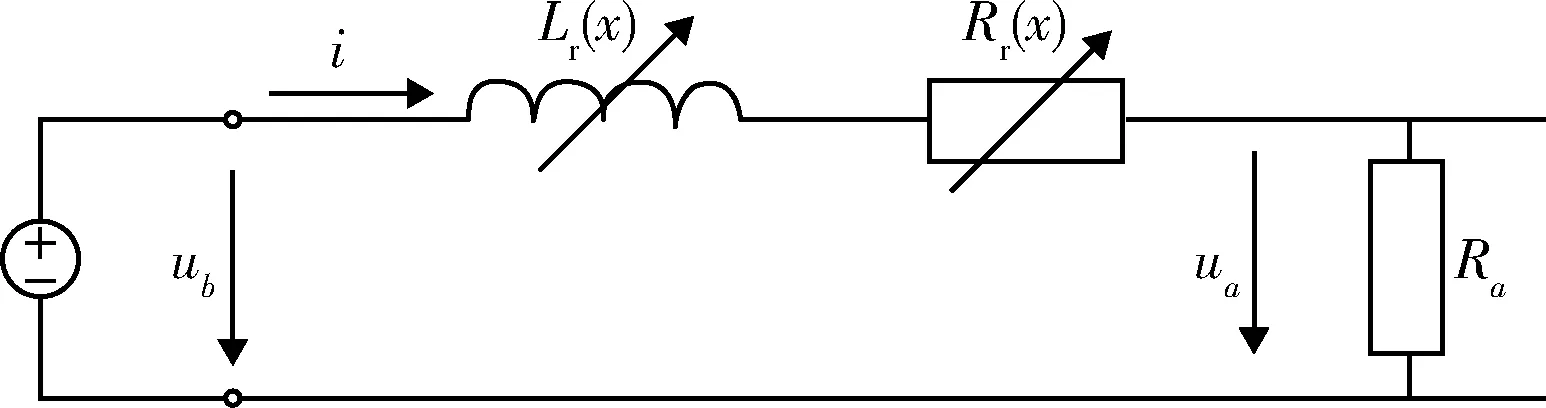
图2 电磁轨道炮系统等效电路Fig.2 Equivalent circuit of railgun

轨道炮系统的电阻和电感模型为

Rr(x)=R0+R′rx，Lr(x)=L0+L′rx,

(1)

式中:R′r，L′r分别为轨道电阻梯度和电感梯度；R0，L0分别为轨道的初始电阻值和电感值，主要由于电连接导致形成;x为电枢在轨道内运动距离。当采用固体电枢时，会带来接触电阻并形成电压降，相对于等离子电枢，固体电枢形成的电压降要小得多。

2 电枢受力分析

考虑轨道炮电流环路的电压降，可知：

(2)

式中:ub,ua分别为电源电压和电枢电压降。电感变化率进一步变换：

(3)

式中：vp为电枢运动速度。所以，

(4)

可以看出，轨道炮电负载特性与电枢运动速度vp和运动距离x相关。

对固体电枢，如果采用平顶脉冲电流激励(定常电流I)，电压

ub=IL′rvp+IR′rx.

(5)

轨道炮等效电阻值可定义为

(6)

进一步将电枢动力学特性和电磁特性关联。忽略摩擦热损耗、电路热损耗等各种能量损失，从能量守恒看，是电源电能转化为弹丸(含电枢)的动能和贮存到轨道电感中的电磁能，即

(7)

式中：Wm，Wk分别为发射器中的电磁能和弹丸(含电枢)的动能；m为弹丸(含电枢)的质量。

显然，轨道炮系统能量时间变化率为

(8)

同时，电源的输出能量恒等于轨道炮的能量变化率(忽略轨道电阻和接触电阻)，则

(9)

化简可得

(10)

考虑到dvp/dt=a，可得

(11)

可见，系统的电感梯度、激励电流是轨道炮中电枢受力的决定性因素。本文将进一步研究轨道炮电枢前的磁场特性，以及与电感梯度、通流长度的关系。

3 电枢前磁场特性分析

由电枢的受力F=0.5L′ri2可知，轨道炮中轨道的电感梯度值是影响电磁轨道炮受力乃至系统性能的核心参数。工程上设计的串联、并联等增强型轨道炮，本质上都是增大轨道发射器系统的电感梯度值[9-12]。

以单轨道系统为例，轨道的有效长度、高度、厚度和轨道间距等几何参数，以及轨道截面形状都直接影响电感梯度值。所以，电感梯度值的设计和计算对轨道炮具有重大意义。电感梯度值的计算通常有解析法和数值法2种途径，本文基于面电流模型，采用解析法研究相关参数对电感梯度的影响。

如图3所示，对于通电导线CD，由毕奥萨伐尔定律可知[1,13-15]，电流I流经有限长导线CD，在距其距离为ρ的P点的电磁感应强度为

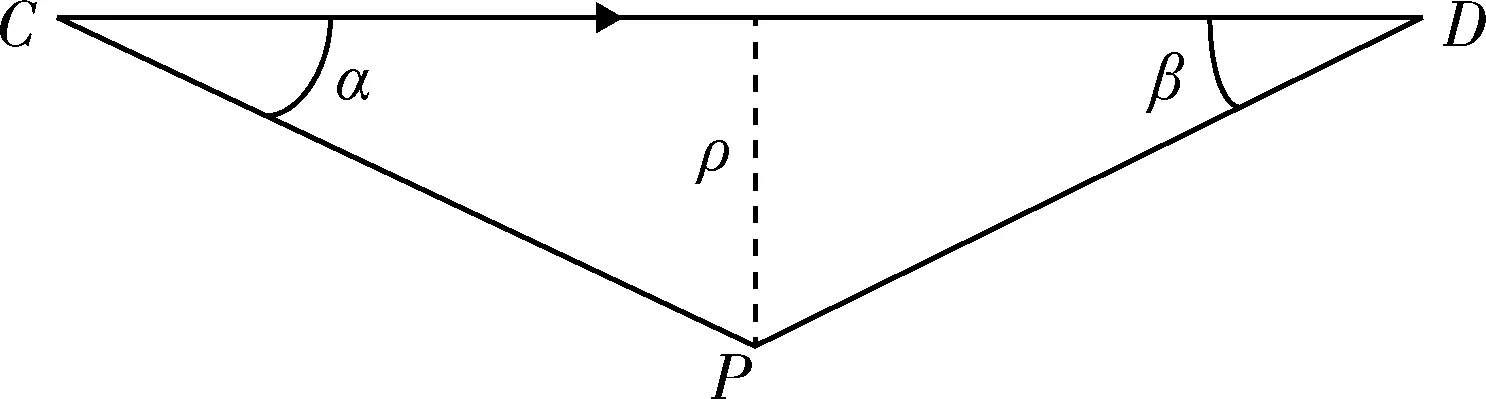
图3 有限长通电导线在某点形成的电磁感应强度Fig.3 Electromagnetic induction intensity formed by a finite length of energized wire at a point

B=μ0I(cosα+cosβ)/(4πρ).

(12)

对于通电导轨，由于电流的趋肤效应和电枢运动后的速度趋肤效应，电流只是在轨道外表面很薄的一层内流过。在一定程度上可将这种电流视为面电流，在此基础上可以较为方便地研究电枢前的磁场特性，以及对电枢受力的影响。同时，忽略电流分布的边缘效应，即假设电枢也是通导电流的金属面结构，电流在轨道面中均匀分布，由此，导轨、电枢的通流结构如图4所示。

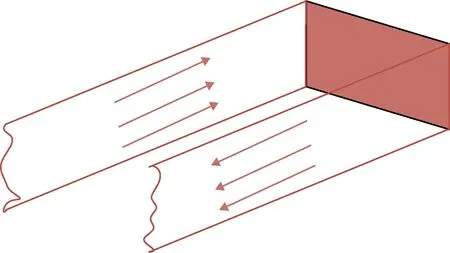
图4 基于面电流的轨道和电枢示意图Fig.4 Illustration of uniform current on rails and armature

对左侧导轨，两导轨之间距离导轨为r的某点P处的电磁感应强度B由安培力的矢量关系可知，垂直于轨道面法线方向且垂直向下分量为有效值，如图5所示。

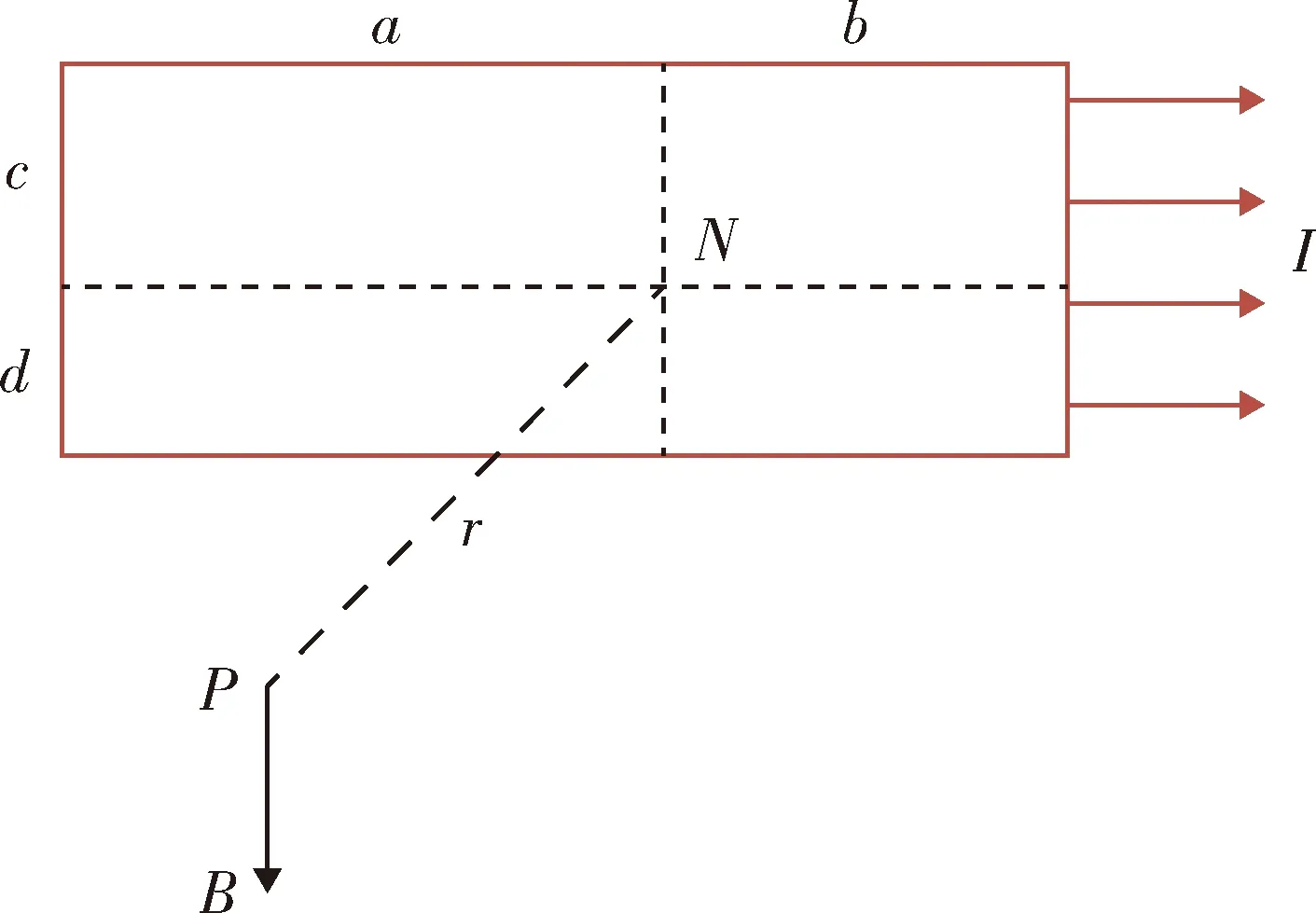
图5 面电流前某点的电磁感应示意图Fig.5 Driving-field at P due to current sheet

对在导轨平板内的电流I，分析其微元线电流dI产生的电磁感应强度dB，计算模型如图6所示。

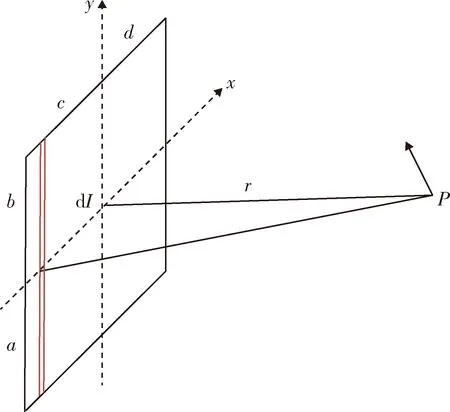
图6 面电流前磁感应强度计算模型Fig.6 Calculation model of magnetic field due to current sheet

其中，假设电流在轨道面内均匀分布，则微元电流dI为

dI=Idx/(d-c).

(13)

对于电枢而言，垂直于其电流方向的电磁感应分量才是有效值，所以在平行于导轨和电枢平面方向，微元线电流dI产生的电磁感应强度为

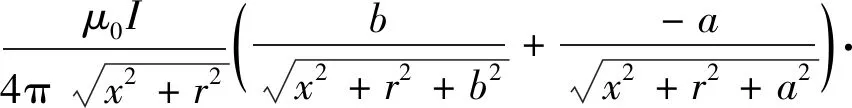
(14)

基于公式(14)，对整个导轨平面积分，可知全部电流I在P点处的电磁感应强度分量为

B(a,b,c,d,r)=10-7I(T1-T2+T3-T4)/(d-c),

(15)

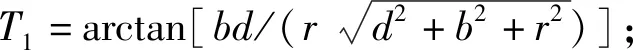
4 仿真及数据分析

基于第3节所建模型开展仿真，并与参考文献[1]的数据进行比对，假设通导电流I=1 MA，轨道尺寸数据a=-100,b=0,c=-1,d=1，对于电枢中心r=1，考虑到轨道的对称性，电枢前的电磁感应强度是由左右两侧导轨通流电流感应磁场叠加而成。

4.1 磁感应强度场分析

文献[1]中,轨道通流长度取值为-∞，计算电枢中心磁感应强度为0.157 T，本文计算中取值a=-100，计算磁感应强度为0.157 1 T，结果与参考文献[1]基本一致。

计算整个电枢前的磁感应强度场，如图7所示。

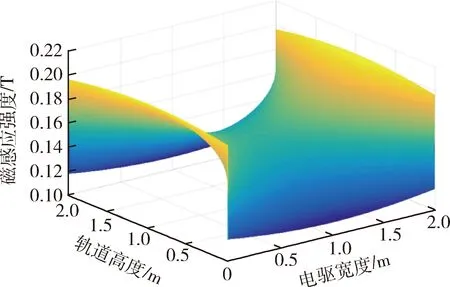
图7 电枢前磁感应强度场Fig.7 Driving-field distribution before armature

从仿真结果可知，电枢前磁感应强度分布场中，电枢与轨道连接处磁感应强度值较高，中间较低，而电枢上下边缘处场强值最低。显然，由于电枢、轨道，以及分布电流的对称性，磁感强度场也自然呈对称性，场强分布结构呈马鞍形。

4.2 电枢的受力分析

基于电磁感应强度场，进而计算整个电枢的受力。

首先采用电枢中心的磁感应强度值作为整个电枢前的有效电磁感应强度值，计算可得：

F=BIL=0.314 (MN).

(16)

作为对比，另采用微元受力积分方法对整个电枢计算受力，由dF=dI×dr×B(a,b,c,d,r)，进而在整个电枢面上进行微元受力积分：

F=∬dI×dr×B=0.314 4 (MN).

可见，基于电枢中心的电磁感应强度值代替精确受力求解，可得到相当精确的近似值。计算可知，电枢中心值近似计算与微元积分计算结果误差仅为0.127%，且近似计算算法中计算量将大大减轻。

4.3 电感梯度计算

由前述分析可知，电磁轨道发射系统中电枢受力F=0.5×L′r×I2，同时，又有F=BIL，由此可计算系统的电感梯度L′r=2BL/I。

将上述参数值代入，可计算系统电感梯度值为

L′r=2BL/I=2×0.157×2/106=0.628 μH.

4.4 “4倍口径法则”

由电磁感应强度模型可知，电枢前的磁感应强度B是电枢后导通电流轨道长度a的函数。通常B值随着轨道通流长度a的增加而变大，进而电枢受力变大。那么是否轨道的通流长度取值越大越好？应该注意到，在上述模型建立过程中，轨道电阻、电流趋肤效应，以及轨道通流后形成的焦耳热等物性特征尚未考虑。导轨通流长度增加后，系统的电阻、电感会增加，同时系统产生的焦耳热也会增加，这都会对系统的效率形成负面影响。

那么轨道通流长度a应如何设计?或者说，电枢的受力与a的关系如何?这对设计弹丸在轨道内的装填深度，以及分布式供电轨道炮系统有重要意义。

通过上两节的电枢受力分析可知，电枢受到的电磁力F=0.5×L′r×I2，系统的电感梯度L′r=2BL/I，可见电枢所受电磁力的根本因素是电磁强度，在不考虑采用使用外加磁场增强方法时，还是要从优化轨道通流后自身形成的感应磁场角度入手。

基于电枢中心点磁感应强度值，研究不同通流长度对B的影响。为更具一般性，模型中的轨道通流长度以轨道炮炮口宽度为基准进行归一化。通过模型计算得出轨道中不同通流长度时，电枢的受力情况，如图8，9所示。

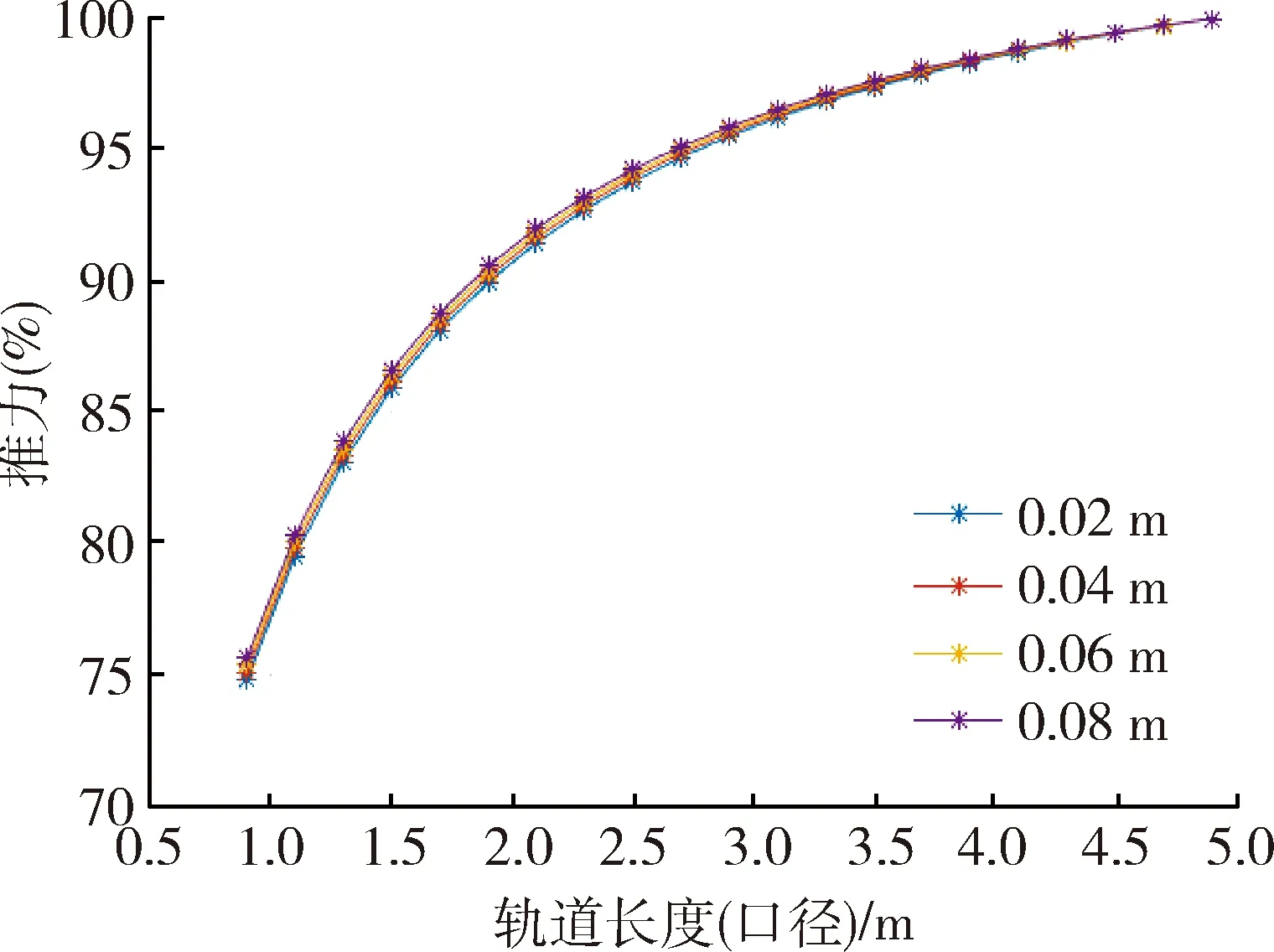
图8 小口径电枢受力随轨道通流长度影响分析Fig.8 Propulsion force as a function of rail-length for small muzzles

图8中，针对用于发射弹丸类小口径轨道发射器，炮口宽度选取2,4,6,8 cm。在图9中，针对用于发射弹体直径稍大的轨道发射器，炮口宽度选取为10,40,70,100 cm。

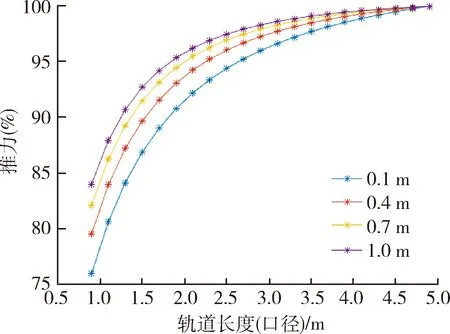
图9 中大口径电枢受力随轨道通流长度影响分析Fig.9 Propulsion force as a function of rail-length for big muzzles

仿真中轨道通流长度从轨道宽度(即炮口内径)的0.9倍长度直到5.0倍长度，并以通流轨道为炮口直径5倍长度时的电枢受力为基准对各种通流长度的电枢受力值进行归一化。可见，轨道炮炮口宽度从2～100 cm范围内，电枢受力随轨道通流长度的变化趋势基本一致，进一步分析可得出如下规律：

(1)随着轨道通流长度的增长，电枢受到的总电磁力增大，随着通流长度的进一步增长，电枢受力增大的趋势放缓。

(2)同等通流长度倍率时，系统的绝对尺寸增大，电枢受力增大，但电枢受力增大趋势逐步放缓。

(3)对不同尺寸的轨道炮，4倍口径的轨道通流长度所能产生的电枢驱动电磁力已能达到最大驱动力的98%，而继续通过增大导轨的通流长度所能增加的电磁推力，不会超过2%。

所以，轨道炮工程设计中弹丸初始装填深度，即轨道的初始通流长度，以轨道口径的4倍值为宜，这样轨道发射器在启动时，电枢即能形成最大驱动力；其次，在设计分布式供电轨道发射器时，通流长度可参考轨道口径的4倍值，这样既可获得系统所能产生的最大推力，同时又避免轨道产生过多的焦耳热和系统损耗，有助提升系统效率和轨道寿命。

5 结束语

本文基于面电流假设，建立了电枢前电磁感应强度场计算模型，研究了电枢前的电磁场分布特性，计算了轨道通流长度对电枢受力影响，验证了“4倍口径法则”。模型中忽略了轨道和电枢的电阻,未来需进一步考虑电流实际分布情况，改进和完善模型，同时与实测数据进行对比，校核模型和参数。