固定单站无源定位可观测性及仿真分析

相飞华，王杰贵

(国防科技大学 电子对抗学院，安徽 合肥 230031)

0 引言

无源定位系统因具有隐蔽性强、探测距离远、适用范围广等特点在电子对抗领域备受关注，其中单站无源定位更是以其独特的优点引人注目[1-2]。对于单站无源定位的可观测性，即考察确定性系统有无唯一解，是定位跟踪的关键前置问题之一[3]。从跟踪算法角度看，是滤波能否收敛于真值；从工程角度看，是能否利用测量到的参数信息解算出目标辐射源的真实位置[4]。

无源被动定位技术需要尽可能地减少定位的约束条件,提高定位方法的可操作性。由文献[1,5]知，通过增加新的观测量，如角度变化率、频率、脉冲到达时间等，能够实现单观测站对辐射源快速定位，同时提高定位的精度和收敛速度。文献[6]利用空域信息和频域信息的定位方法，可以实现对匀速运动的辐射源的瞬时定位，定位速度快且定位精度高，其应用前景广泛。文献[7]给出了目标有限阶运动条件下利用角度和多普勒频率变化率测量信息的可观测条件。文献[8]给出了利用方位角及其变化率为观测量，目标与观测器不同相对运动状态下的可观测条件。文献[9]对N阶多项式机动的可观测性进行了分析,得到了只测向时可观测性的充要条件。文献[10]指出方位角与角速度，多普勒频率与多普勒频率变化率所提供的可观测性信息一致。文献[11-13]给出了不同方法下利用TOA(time of arrival)和DOA(direction of arrival)观测量对匀速直线运动目标的可观测性条件。文献[14-15]以目标方位角和多普勒频率为观测量，对匀加速和匀转弯运动进行了可观测性分析。

以往的研究多关注于运动单站对固定目标或运动目标，而对于可观测性弱、非线性强的固定单站对运动目标研究较少。本文在固定单站二维平面条件下，为实现快速定位，增加角速度观测量，以目标辐射源的方位角、角速度和多普勒频率变化率为观测量。在可观测性分析过程中，先对比角度与角速度变化率，多普勒频率与多普勒频率变化率所提供的可观测性信息；再对观测方程伪线性化处理，应用线性系统理论，简化分析过程，避免求解复杂的雅可比矩阵；最后对目标进行匀速直线运动、匀加速直线运动目标和匀转弯运动3种不同状态下的可观测性进行了理论推导，给出可观测性条件，并进行了仿真验证。

1 固定单站无源定位模型

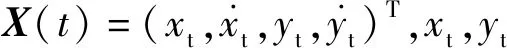
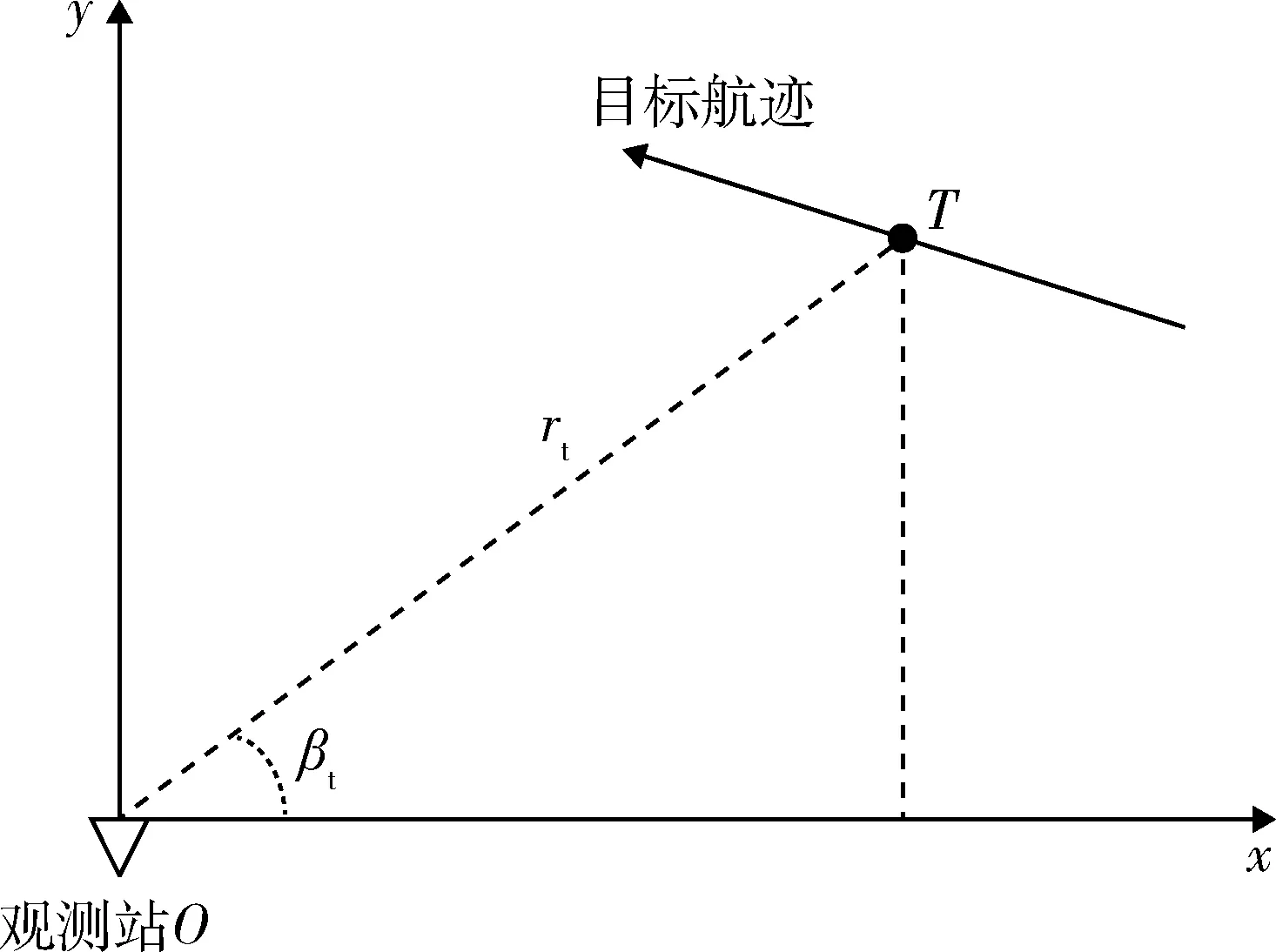
图1 固定单站无源定位二维平面图Fig.1 Two-dimensional plan of fixed single station passive location

Z(t)=h(X(t))+V(t),

(1)

式中：V(t)表示量测噪声，是均值为0的高斯白噪声，其协方差矩阵为R(t)。从固定单站的定位模型，可获得空域和频域信息。

1.1 空域信息

考虑图1所示的线性离散系统，在t时刻，目标辐射源相对于观测站O的径向距离为r(t)，相对x轴正方向的夹角方位角为β(t)。由几何知识可知：

(2)

(3)

1.2 频域信息

当目标辐射源相对于观测站径向运动时，会产生多普勒效应，观测站接收到的频率包含有多普勒频率，假设目标辐射源信号频率在观测时间内保持恒定，则有

f(t)=fT+fd(t)，

(4)

式中：f(t)为观测站接收到的目标辐射源频率；fT为目标辐射源信号频率；fd(t)为多普勒频率，由相对径向运动产生。多普勒频率fd(t)的表达式为

(5)

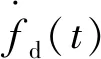
(6)

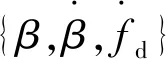
(7)

2 可观测性分析

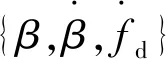
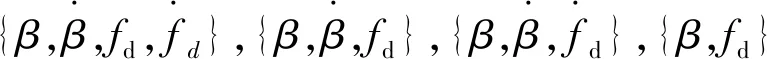
证明：

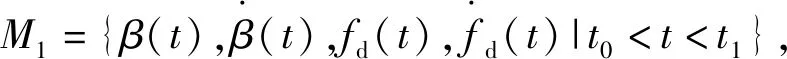
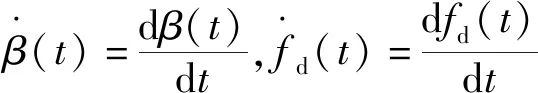
综合(1)和(2)，可得到S2=S1。证毕。

由上述分析，对方位角和多普勒频率信息进行分析，式(2),(5)线性化处理可得

0=xtsinβt-ytcosβt,

(8)

(9)

2.1 线性系统的可观测原理

从本质上讲，噪声的存在并不会对定位系统的可观测性产生影响，只会定位系统的定位精度与跟踪算法收敛速度等产生影响。为了考察定位系统的可观测性，假定系统为理想情况，即系统中不存在状态噪声和观测噪声。

对于理想连续线性系统，其状态方程和观测方程为

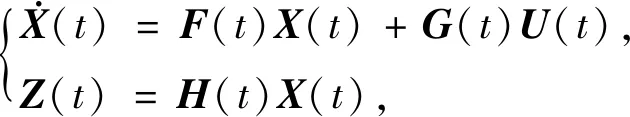
(10)

式中：X(t)为n×1维状态矢量；F(t)为n×n维状态矩阵；G(t)为n×r维控制矩阵；U(t)为r×1维状态控制矢量；Z(t)为m×1维观测矢量；H(t)为m×n维测量矩阵。

状态方程及观测方程均为线性方程，根据线性系统理论，下面给出状态方程的通解为

(11)

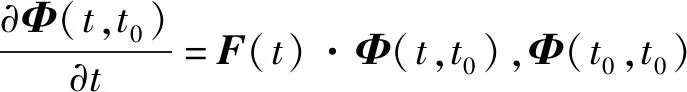
上述线性系统，在[t0,t1]可观测的充要条件为：∀Y≠0∈Rn，∃t∈[t0,t1]使得H(t)Φ(t,t0)Y≠0。其逆否命题又可表述为：∀t∈[t0,t1]，若H(t)·Φ(t,t0)Y=0，则Y=0。该结论即为线性系统的可观测条件，可用于对无源定位中的系统可观测性进行分析[14-15]。

2.2 匀速直线运动的可观测分析

(12)

X(t)=Φ(t,t0)X(t0)，

(13)

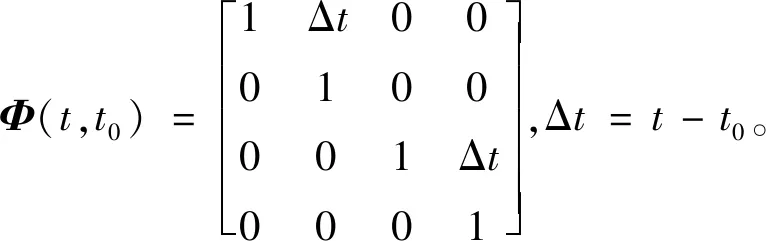
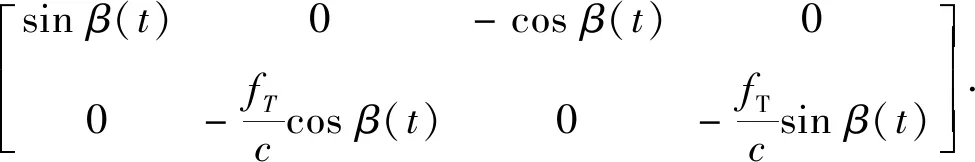
(14)

假设存在Y=(y1,y2,y3,y4)T，使得∀t∈[t0,t1]，有H(t)Φ(t,t0)Y=0。计算并化简可得：

(y1+Δty3)sinβ(t)-(y2+Δty4)cosβ(t)=0,

(15)

y2cosβ(t)+y4sinβ(t)=0.

(16)

对式(16)求导可得

(17)

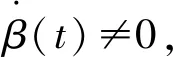
y2cosβ(t)+y4sinβ(t)=0.

(18)

又知正弦函数与余弦函数之间是线性无关的，因此容易求得y3=y4=0，将解代入式(15)得到

y1sinβ(t)-y2cosβ(t)=0.

(19)

同理可知y1=y2=0，至此得出Y=0。

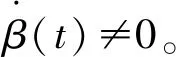
2.3 匀加速直线运动的可观测分析

目标辐射源作匀加速运动时，其在理想情况下，连续时间的状态方程为

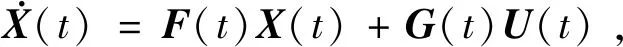
(20)

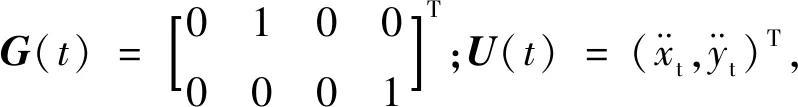
仍然利用线性系统的可观测原理进行分析，容易发现，当目标处于匀加速直线运动状态时与匀速直线运动状态时，具有相同的方程，则其推导结果必定一致。因此，2种运动状态下的可观测性条件是相同的，即当目标辐射源处于匀速直线或者匀加速直线运动状态时，不可朝观测站作径向运动。

2.4 匀转弯运动的可观测分析

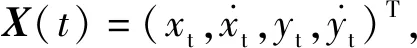
(21)

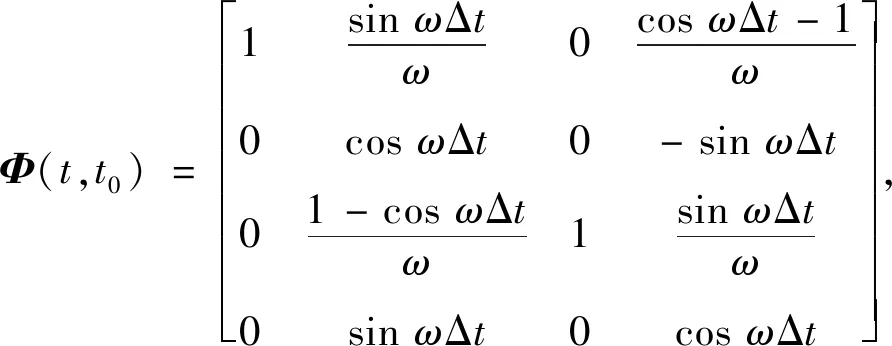
假设存在Y=(y1,y2,y3,y4)T，使得∀t∈[t0,t1]，有H(t)Φ(t,t0)Y=0。计算并化简可得

cos[β(t)-ωΔt]y2+sin[β(t)-ωΔt]y4=0.

(22)

继续对两边求导可得

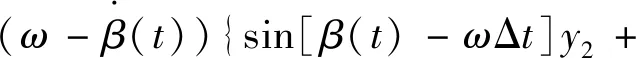
(23)

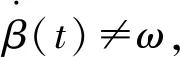
sin[β(t)-ωΔt]y2+cos[β(t)-ωΔt]y4=0.

(24)

容易得到：y2=y4=0，同理可得，y1=y3=0，至此得到Y=0。

由以上分析知，目标辐射源作匀转弯运动时(转弯率为ω)，可观测性条件为：目标辐射源到观测站的角速度不能等于转弯率，即目标辐射源不能绕观测站作圆周运动。

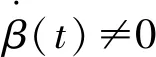
3 仿真校验

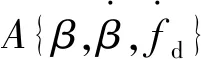
实验1：

(a)目标作匀速直线运动，初始位置为(120,90)km，速度为(-200,100)m/s；

(b)目标作匀速直线运动，初始位置为(120,90)km，速度为(-200,-150)m/s。

实验2：

(a)目标作匀加速直线运动，初始位置为(120,90)km，速度为(-200,100)m/s，加速度为(-2,1)m/s2；

(b)目标作匀加速直线运动，初始位置为(120,90)km，速度为(-200,-150)m/s，加速度为(-2,1.5)m/s2。

实验3：

(a)目标作匀转弯运动，初始位置为(40,30)km，速度为(150,200)m/s，转弯率为5 mrad/s；

(b)目标作匀转弯运动，初始位置为(50,0)km，速度为(0,250)m/s，转弯率为5 mrad/s。

定位跟踪采用容积卡尔曼滤波(cubature Kalman filter,CKF)算法[18-19]，用相对距离误差(relative range error,RRE)作为衡量指标,定义式为

(25)

仿真进行100次Monte Carlo实验，结果如图2～4所示。

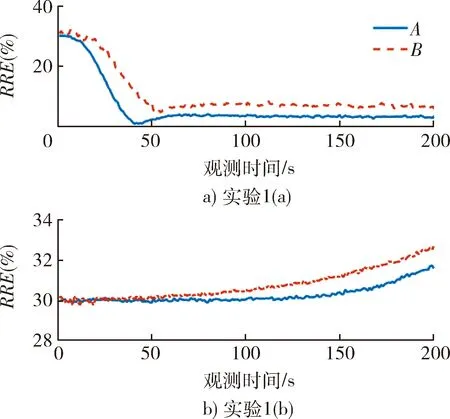
图2 匀速直线运动仿真结果Fig.2 Simulation of constant velocity target

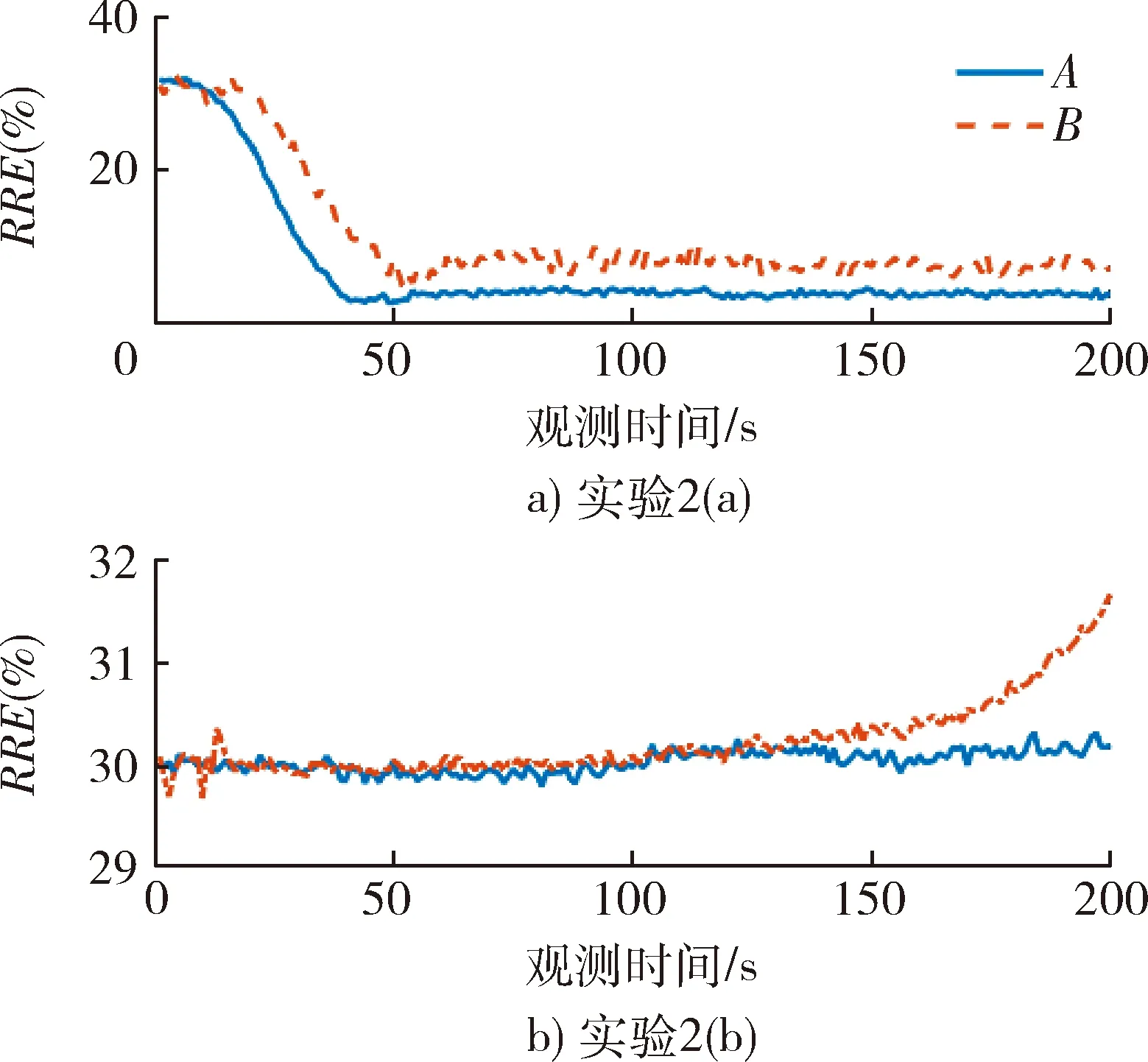
图3 匀加速直线运动仿真结果Fig.3 Simulation of constant acceleration target

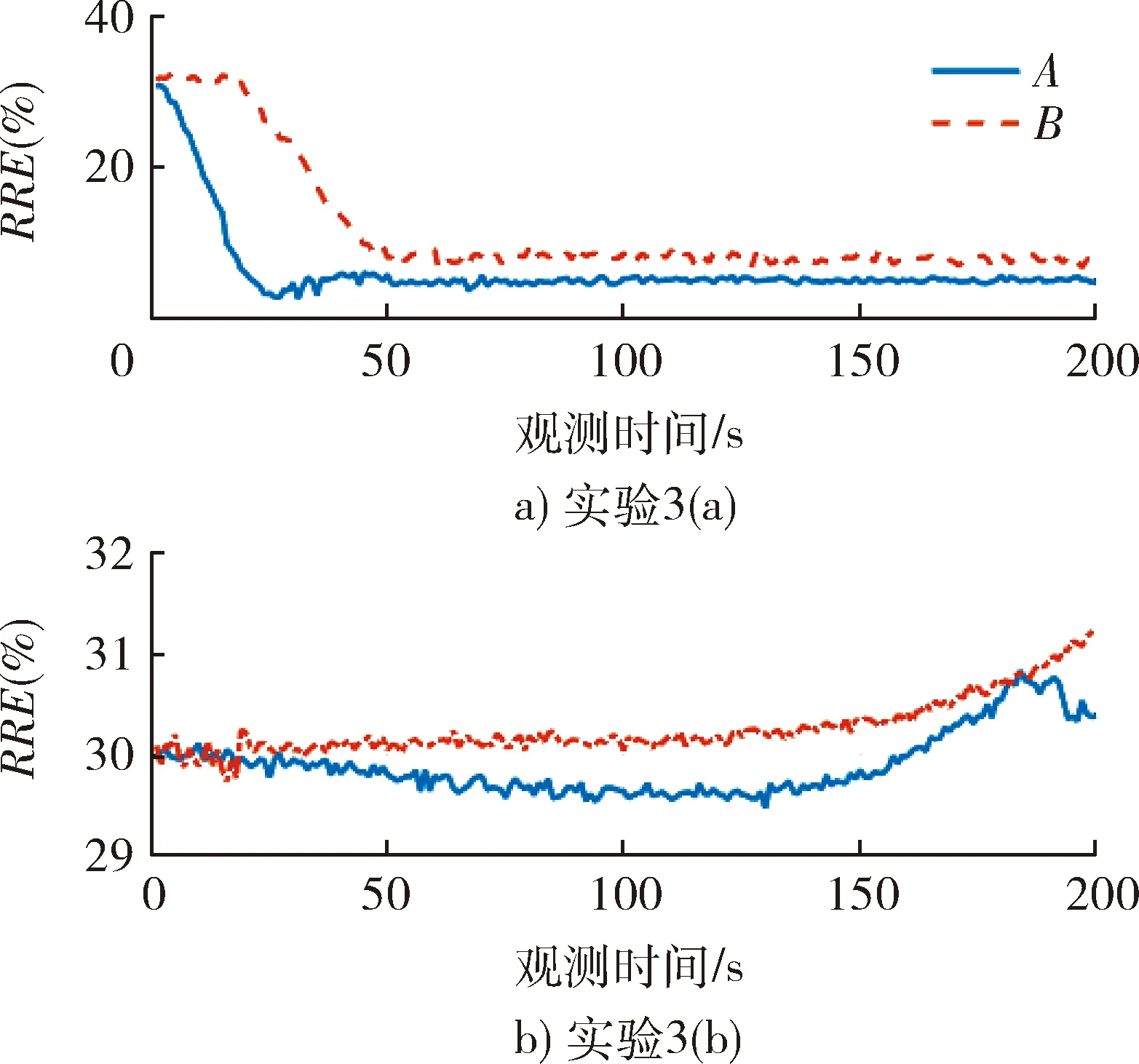
图4 匀转弯运动仿真结果Fig.4 Simulation of constant turn rate target

图2～4中，曲线A表示观测集A滤波结果，曲线B表示观测集B滤波结果。当目标辐射源运动方式满足可观测性条件时(3个实验中(a)例)，利用观测集A和观测集B均可以实现固定单站对不同运动状态目标的无源定位，经过一段时间跟踪后，滤波结果逐渐收敛。同时可以看出的是，在匀速、匀加速和匀转弯运动状态下，相对于观测集B，观测集A定位收敛速度更快，滤波精度更高。因此在满足可观测条件下，增加观测量以改善定位跟踪性能具有一定的实际意义。

当可观测性条件不被满足(3个实验中(b)例)，即目标匀速、匀加速朝观测站径向运动或目标绕观测站圆周运动时，无论利用观测集A或是观测集B均无法实现对目标的定位跟踪，滤波结果不随时间收敛，且趋向于发散。仿真实验的结果与上文的可观测性分析一致，从而验证了理论分析的正确性。

4 结束语

本文采用方位角、方位角变化率和多普勒频率变化率为观测量，将观测方程伪线性化处理后，利用线性系统的可观测理论，对目标辐射源不同运动状态的可观测性进行了具体分析，得出了可观测的条件。仿真分析验证了理论分析的正确性，目标辐射源作匀速直线或者匀加速直线运动时不能朝观测站作径向运动，目标辐射源作匀转弯运动时不能绕观测站作圆周运动。