决策树集成方法在反舰导弹效能评估中的应用

姬正一，陈阳，沈培志，韩先平，齐鸿坤

(1.中国人民解放军92941部队，辽宁 葫芦岛 125000；2.中国人民解放军92493部队，辽宁 葫芦岛 125000；3.海军航空大学，山东 烟台 264001)

0 引言

反舰导弹是打击海上目标的主战武器装备，是决定海上作战任务成败的关键因素，科学评估反舰导弹武器系统的作战效能，将对指挥决策起着至关重要的作用[1-2]。反舰导弹武器系统作战效能评估经典方法(以下简称为经典方法)是采取结构化的方式构建模型，例如层次分析法、模糊综合评价法、集对-指数分析法等[3]，通过科学划分能力层级、专家打分等方式建立一套完整的能力指标体系，能够较为合理地评价反舰导弹武器系统作战效能。

在实际应用中，经典方法同时存在一些弊端，在能力分层、权重设计与归一化评分等方面都需要依靠主观经验确定，并且在处理实战环境下的大数据、非结构化样本时，计算复杂度和时间成本较高[4]。

伴随大数据时代来临，数据资源的获取变得更加容易，基于先验信息的机器学习方法在军事领域的应用将成为一种趋势[5]。本文以数据为驱动，通过效能评估指标体系构建特征工程，结合经典方法建立随机森林和梯队提升回归树2种决策树集成的机器学习效能评估模型，并将2种方法分别与经典方法进行了对比，以检验决策树集成方法在反舰导弹作战效能评估中的应用效果。

1 作战效能评估指标分析

1.1 评估指标体系建立

随着信息化技术快速发展，反舰导弹武器系统组成越发复杂，效能评估涉及诸多因素，尤其在实战环境下，要将导弹系统自身战技性能与复杂战场环境等影响综合考虑[6]，对作战效能评估方法提出了较高要求。为综合评估武器系统效能，美国工业界武器系统效能咨询委员会提出了ADC(availability dependability capacity)通用评估模型[7]，它把系统效能指标表示为武器系统可用度、任务可信度和系统能力的函数，即系统效能E是有效度向量A、可信度矩阵D和能力矩阵C的乘积，表达式为

E=ADC.

(1)

ADC评估主要考虑的是武器系统自身性能要素的影响，而现代战争中任何装备的使用都离不开作战环境。实践表明，反舰导弹武器系统信息化程度越高，作战环境对其作战效能的影响就会越大[8]。因此，要使评估更加具备现实意义，必须对实战环境加以考虑，为衡量反舰导弹武器系统复杂战场环境的适应能力，增加了战场环境影响因子H，改进后的ADC模型[9]为

E=ADCH.

(2)

在充分考虑反舰导弹武器系统性、客观性、独立性、层次性以及一致性的基础上，按照定性、定量相结合的原则分析构建反舰导弹武器系统作战效能评价指标体系。

(1)反舰导弹武器系统有效度A由系统的维修率和故障率组成。

(2)可信度D由系统的飞行控制可靠性、发射可靠性和命中毁伤可靠性组成。

(3)作战能力C：第1层指标由反舰导弹的突防能力、选择捕捉能力、命中能力和毁伤能力组成；第2层指标中的捕捉能力由雷达覆盖能力、雷达制导方式和雷达截获能力组成，第2层指标中的突防能力由隐身性能和飞行性能组成，第2层指标中的命中能力由命中密集度和命中准确度组成，第2层指标中的毁伤能力由导弹战斗部性能和引信性能组成。

(4)战场环境适应能力H：第1层指标包括电磁环境和自然环境适应能力；第2层指标中的电磁环境适应能力包括抗敌电磁干扰、抗战场自然电磁干扰和装备系统间电磁兼容能力，第2层指标中的自然环境适应能力包括海洋水文环境(海浪、能见度)和海洋气象环境(风、温度、气压)。

该指标体系中故障率、维修率、发射可靠性、飞行控制可靠性等19个能力指标将作为后续2种决策树集成模型的19个数据特征，改进ADC评估模型求出的反舰导弹作战效能E将作为模型的数据标记值。评价指标体系如图1所示。

1.2 评估指标各分量的求取方法和思路

1.2.1 有效度A

当武器系统在任意时间工作时，有效度A表示系统在开始执行任务时所处状态的指标。由于反舰导弹武器系统由火控系统和导弹系统组成，单一系统的初始状态一般情况下可分为正常工作和故障维修2种状态，对于反舰导弹武器系统可以有4种状态，其有效向量A为

A=(a1,a2,a3,a4)，

(3)

式中：a1为导弹系统和火控系统均正常工作的概率；a2为导弹系统正常工作、火控系统故障的概率；a3为导弹系统故障、火控系统正常工作的概率；a4为导弹系统和火控系统均故障的概率。对于单一系统或平台来说，处于正常工作状态的概率为

(4)

式中：MTBF为平均故障间隔时间；MTTR为平均故障修复时间；λ为故障率；μ为修复率。

1.2.2 可信度矩阵D

可信度D是对系统在开始执行任务处于某一状态而结束时处于另一状态的系统状态转移性指标表述，反映了系统可靠性的好坏。按照评估指标体系，可信度取决于发射可靠性、飞行控制可靠性和命中毁伤可靠性3个指标，由于反舰导弹武器系统自身不可修复，若在开始执行任务时各系统发生故障，则整个任务过程中不会正常工作[10]。假设执行任务时反舰导弹武器系统的故障率服从指数定律，则发射系统可靠性Rm、飞行控制系统可靠性Rk、命中毁伤系统可靠性Rs分别为

(5)

式中：λm,λk,λs分别为发射系统、飞行控制系统和命中毁伤系统执行任务时故障率;Tm,Tk，Ts分别为发射系统、飞行控制系统和命中毁伤系统执行任务的持续时间。

考虑到飞行控制系统和命中毁伤系统均为弹上系统，为使可信度矩阵计算较为便捷，使弹上系统可靠性Rh表示为

Rh=RkRs.

(6)

由此可得可信度矩阵为

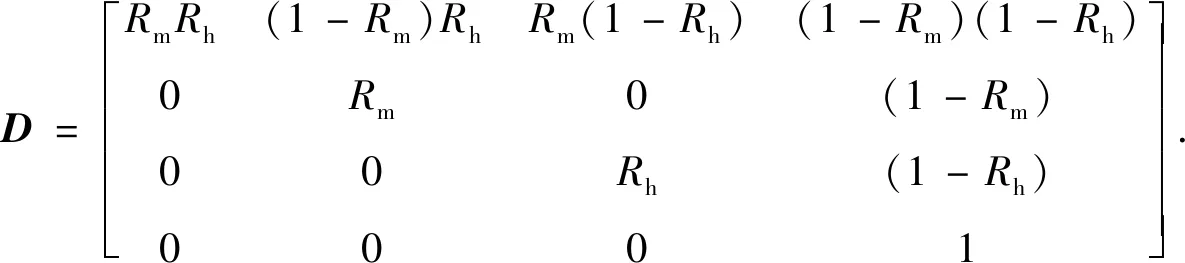
(7)

1.2.3 作战能力矩阵C

表示系统完成规定任务能力的指标。在图1中对反舰导弹作战能力进行系统分析，划出选捕、突防、命中、毁伤4个能力指标以及雷达覆盖能力、制导体制等9个子能力指标，计算时先分别找出与9个子能力指标对应的装备性能参数，然后采取指数分析法进行计算，反舰导弹武器系统作战能力C可表示为

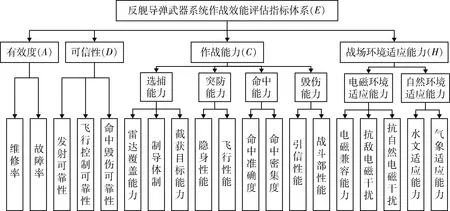
图1 反舰导弹武器系统作战效能评估指标体系Fig.1 Operational effectiveness evaluation index system of anti-ship missile weapon system

(8)

式中：C1,C2,C3,C4分别表示选捕、突防、命中和毁伤能力;DR为末制导雷达作用距离，反映子能力指标中的雷达覆盖能力；AR为末制导雷达航向跟踪范围，S为末制导雷达距离跟踪范围，反映雷达截获目标能力；ε为有无复合制导体制影响因子，反映雷达制导体制影响因素；I为RCS反射面积，反映导弹隐身能力；H为最大巡航高度;L为最大有效射程;M为巡航速度，反映导弹飞行性能；P为单发命中概率，反映导弹命中准确率；Q为自控终点散布误差，反映导弹命中密集度；Y为引信灵敏度，反映引信性能；G为战斗部质量，反映战斗部性能；w1,w2,…,w11为指标权重。利用层次分析法(analytic hierarchy process,AHP)进行指标权重分配，然后采用集对分析法对指标体系进行处理，即通过构造理想矩阵的指标向量方式形成联系矩阵，再与所得的权重系数进行线性叠加，即可求出能力矩阵C。

1.2.4 战场环境适应能力矩阵H

考虑到战场环境影响因素的复杂性、动态性，为了较为客观反映反舰导弹的战场环境适应能力，采取以下步骤计算：

(1)指标量化：由于抗敌电磁干扰、抗战场自然电磁干扰、装备系统间电磁兼容能力以及海洋水文环境和气象环境适应能力5个子指标既有定量数据又有定性描述，故依据军事用户给出的性能参数一些常用范围值，广泛征询专家意见，采取专家打分、归一化处理的方法得出具体的量化值，且这些值范围在0到1之间。

(2)确定权重系数：按照AHP法分别计算一级指标和二级指标对应的权重系数。首先采取1-9标度法构造判断矩阵；其次通过一致性检验判断矩阵是否协调一致避免相互矛盾；利用方根法求出判断矩阵的特征值与特征向量，得出相应的权值[9]。

(3)用线性加权和法确定战场环境适应因子H：

(9)

式中：μi,μij分别为一级指标和二级指标的权重系数;Fij为5个子指标的专家打分值;m为一级指标数量;ni为第i类一级指标中二级指标数量。

在分别得出有效度A、可信度D、作战能力C和战场环境适应能力H后，按照式(2)计算得到的系统综合效能值作为决策树集成模型数据样本的标记值，每个标记值和相应的19个特征值构成了一条完整数据。

2 反舰导弹武器系统决策树集成评估方法

决策树集成是机器学习领域有监督学习的一类重要算法，它以决策树为基础构建基本分类器，集成无数个基本分类器开展分类和预测任务[11]。本文用到的2种决策树集成方法分别是随机森林算法和梯队提升回归树算法，随机森林中决策树为随机构建，预测结果取决于投票众数；梯度提升树中决策树为层层递进，预测结果取决于最后一颗树。

2.1 决策树

作为基本分类器，决策树本身就是一种学习预测模型，从一层层if/else问题中进行学习并得到结论，根据信息增益或基尼系数的大小来决定先分类哪一个特征[12]。本文策略是从根节点到叶节点采用递归的方法，构建信息熵下降最快的树，信息熵可以用来度量每一个节点上的信息量与不确定性，它的大小通常与事件发生的概率相反，公式为

(10)

式中:P(xi)为某事件发生的概率。针对多个变量时，常用联合熵来表征一个节点上的信息量与不确定度，计算公式为

(11)

通常情况下，联合熵会大于每一个单独的信息熵，小于所有独立的信息熵之和，并且联合熵与某个变量的信息熵的差称之为条件熵，公式为

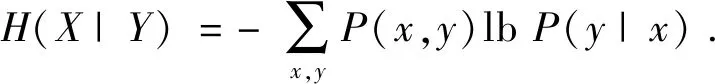
(12)

信息熵的差值用信息增益(Gain)来表示，能够影响决策树的选择，向下分裂时优先选择信息增益大的，信息增益的计算公式为

Gain=Hb-Ha∂t，

(13)

式中：Hb为分裂前信息熵；Ha为分裂后信息熵；∂t为加权平均数。

决策树算法运行效率高，对数据适应性强，不需要特征归一化处理，但会出现过拟合，且泛化能力较弱，因此在实际应用中往往使用集成的方法有效解决上述问题。

2.2 随机森林模型

随机森林(random forest,RF)算法是多颗随机决策树的集合，利用每棵树对特征和样本采样的差异性，有效降低过拟合，提升整体泛化能力[13]。该算法建立反舰导弹作战效能评估模型的主要步骤如下(图2)：

图2 随机森林算法结构Fig.2 Algorithm structure of random forest

(1)运用连续变量离散化或缺失数据插值等处理手段，对反舰导弹数据集进行预处理，再将数据集分为训练集和测试集。

(2)假设训练集中包含有N个样本(反舰导弹的N种状态)，T种分类属性(每种状态下的T个特征)，采用Bootstrap抽样方法得到新的样本集。

(3)在设定的T种特征中，随机抽取t(t≤T)种特征，使用某种决策树最优特征标准，选择最优分类节点。

(4)对步骤(3)重复进行K次，生成K棵决策树。

(5)对这K棵决策树的预测结果采取投票机制，根据投票结果决定最终的效能预测数据。投票机制的函数模型如下：

(14)

式中：hi(x)表示第i棵决策树的预测值；Y表示目标变量(分类标签或预测值)；arg max表示找出能够使函数取到最大值的自变量。

随机森林将多个弱分类器组合使用，得到一个分类性能更好的强分类器，经过训练后相比较于决策树分类器模型泛化能力更强，故在反舰导弹作战效能评估中首选了随机森林算法模型。同时每棵决策树是独立同分布的，便于并行化处理数据，且不需要数据集标准化归一化处理，效率较高[14]。

2.3 梯度提升回归树模型

梯度提升回归树(gradient boosting regression tree,GBRT)是基于误差函数的一种优化算法，通过集成弱分类器来生成一种强分类器。首次计算由基本模型完成，而下次计算是为了减小上次模型的残差(residua)，在残差梯度(gradient)方向新建立一个新的模型，通过持续调整优化弱分类器权重，逐渐减小损失函数，到达阈值后形成一个强分类器[15]。该算法建立反舰导弹作战效能评估模型的主要步骤如下(图3)：

图3 梯度提升回归树算法结构Fig.3 Algorithm structure of gradient boosting regression tree

(1)假设损失函数为L(y,f(x))，每一棵回归树的叶节点数为J，其输入空间分割为J个不相交区域R1m,R2m,…Rjm，对每一个区域估计一个常量值bjm。回归树用公式表示为

(15)

(16)

(17)

(3)对弱分类器进行迭代，迭代次数为m(m=1,2,…,M)，样本为i(i=1,2,…,T)，计算第m轮第i个样本值的残差(即第m-1轮损失函数的负梯度)，计算公式为

(18)

(4)使用(xi,rmj)来拟合一棵新的即第m棵树gm(x)，其对应的叶节点区域为Rjm,j=1,2,…,J，J为叶节点个数，并计算梯度下降的步长，计算公式为

(19)

(5)更新强分类器，每一轮损失函数的计算都是与yj比较，故需加上本轮的，计算公式为

(20)

(6)得到强分类器，并计算输出数据，数据计算公式为

(21)

梯度提升决策树能够灵活处理各种类型的数据，包括连续和离散值，用较少的训练时间能得到预测准确率较高的模型。但由于弱分类器之间存在依赖关系，难以并行开展训练。

3 效能评估算例仿真

3.1 样本数据准备

拟定反舰导弹武器系统的火控子系统平均故障间隔为1 500～2 100 h之间，平均修理时间为40～50 h之间，导弹子系统平均故障间隔时间为2 000～3 000 h之间，平均修理时间为80～100 h之间，执行任务时间为10～25 min之间，有复合末制导体制的反舰导弹ε=1，无复合末制导体制的ε=0.5～0.9。不同状态的反舰导弹战术技术性能指标如表1所示，战场环境适应因子如表2所示。为提供足够的训练和测试数据，本文共收集了240种不同状态的反舰导弹性能数据。

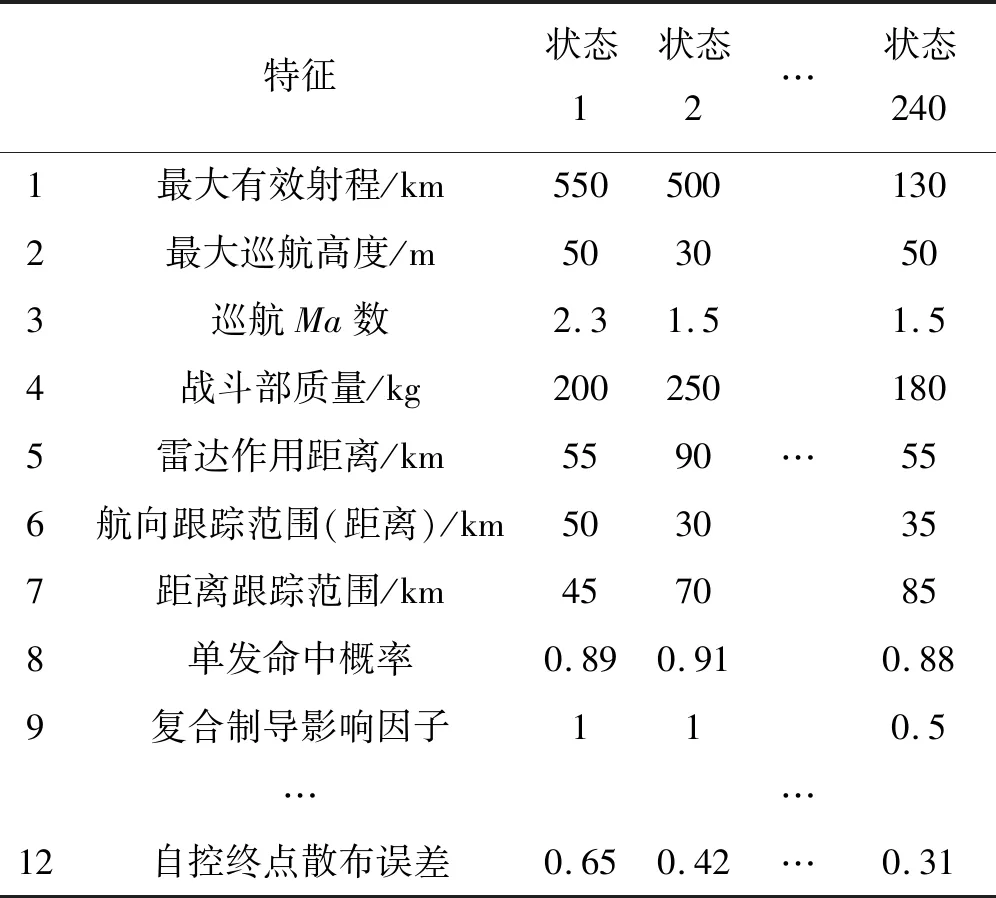
表1 反舰导弹武器系统战术技术性能指标Table 1 Tactical and technical performance index of anti-ship missile weapon system

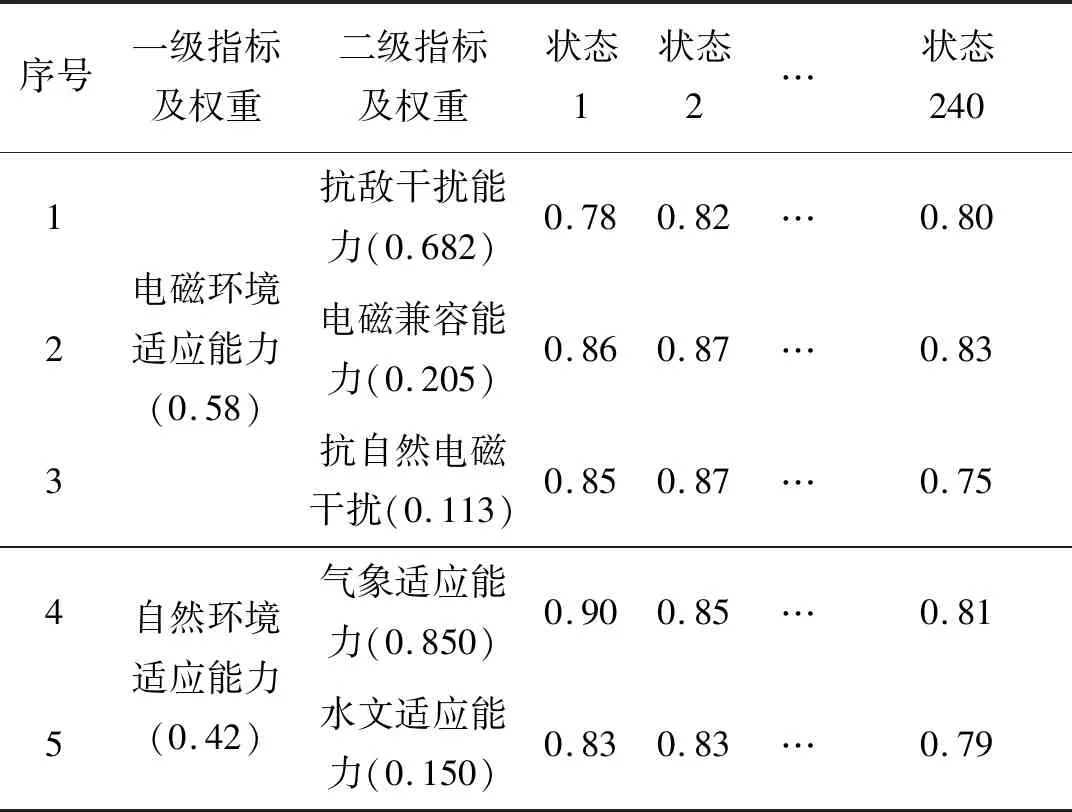
表2 反舰导弹武器系统战场环境适应因子Table 2 Battlefield environment adaptive factors of anti-ship missile weapon system

对每一种状态的反舰导弹分别求出有效度A、可信度D、作战能力C和战场环境适应能力H后，按照公式(2)计算得到的系统综合效能值E。

不同状态的反舰导弹有效度A分别为

A1=(0.952 26,0.021 76,0.025 39,0.000 5),A2=(0.941 24,0.028 23,0.029 63,0.000 8),…
A240=(0.942 1,0.021 19,0.035 88,0.000 8)

可信度D分别为

作战能力C分别为

C1=2.236 38，C2=1.829 9，…
C240=0.955 45，

战场环境适应能力H分别为

H1=0.832 679,H2=0.800 567,…
H240=0.820 023.

经计算得系统综合效能值E分别为

E1=0.529 8,E2=0.789 9,…,E240=0.270 1。系统的综合效能E将作为数据集的标签值。

3.2 随机森林模型仿真

随机森林评估模型选择以信息熵作为分类标准，以R2分数作为评定标准，为获取最优模型，需要调参选择最优参数，用K折交叉验证(K-fold cross validation)方法测试模型的泛化能力，用网格搜索(grid search)算法循环遍历候选参数并以交叉验证结果作为指标得到最优参数。树最大深度和决策树数量是随机森林模型中较为重要的2个参数，通过搜索，决策树数量为200，最大深度为40，2个参数的寻优平均分数热图如图4所示。

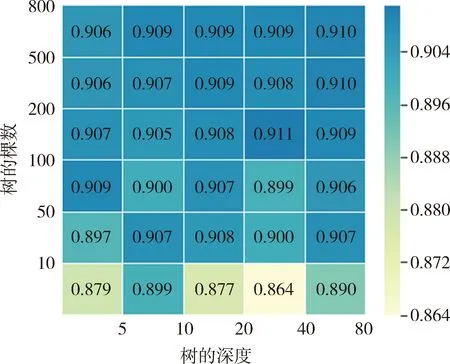
图4 RF模型决策树个数和最大深度平均分数热图Fig.4 Number of decision trees and maximum depth average fractional heatmap of RF model

其他参数取值范围由反舰导弹数据集样本条件初定，采取随机搜索寻找最优取值，随机森林模型参数的范围及优选取值如表3所示。

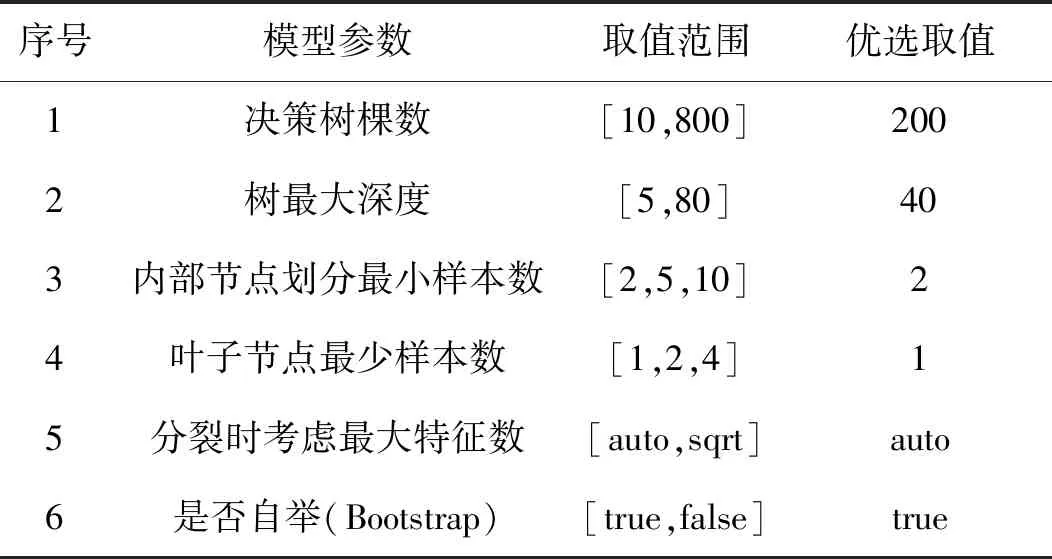
表3 随机森林模型参数选择Table 3 Parameter selection of RF model

仿真结果表明，与改进ADC评估模型求出的反舰导弹作战效能E相比较，随机森林算法在测试集中评估预测性能较好，输入特征值后，模型的预测准确率为92%。两者对比如图5所示，其中红线为改进ADC评估模型求出的反舰导弹作战效能标签值，绿线为随机森林模型预测值。

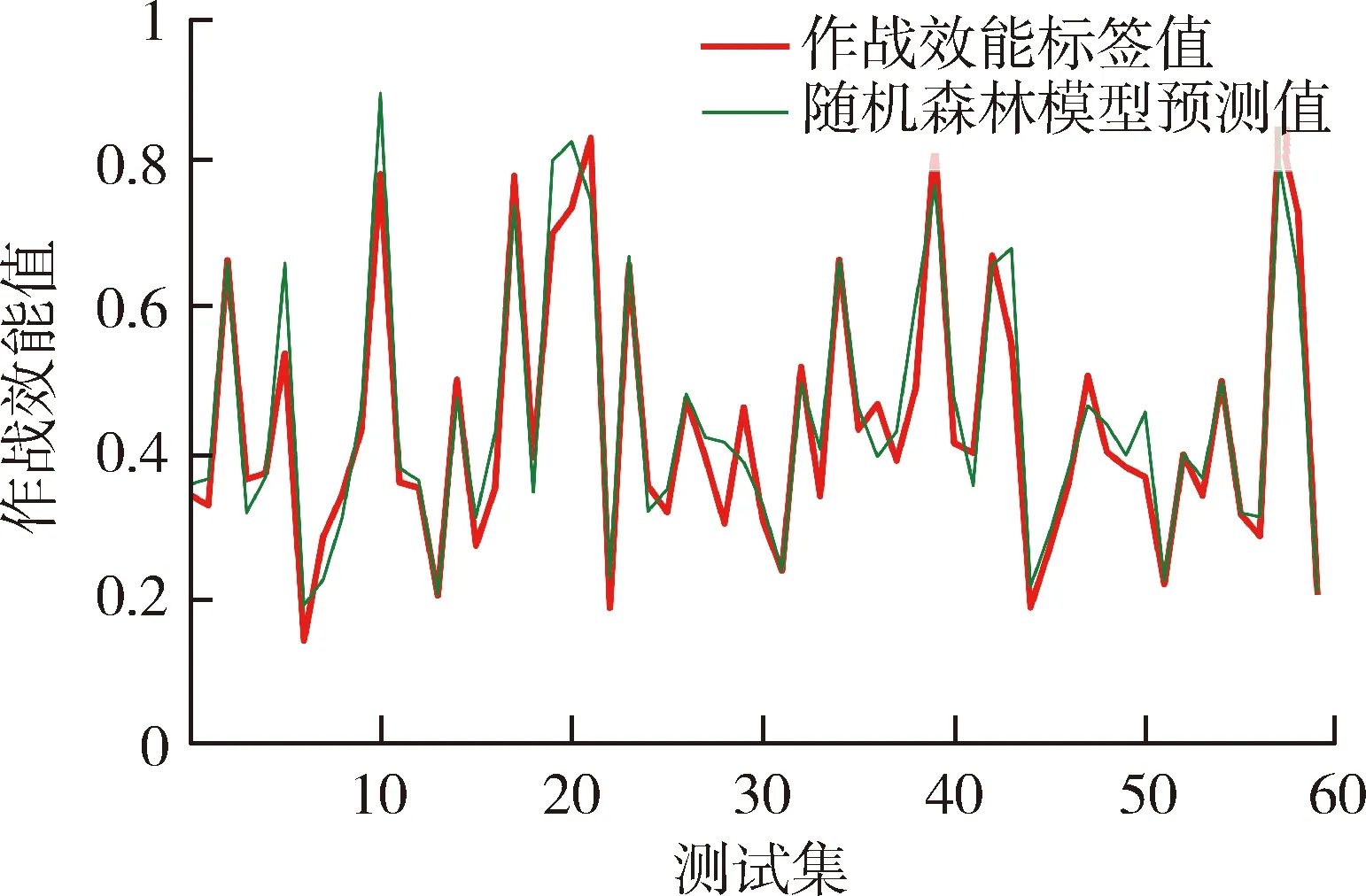
图5 随机森林模型预测结果与反舰导弹作战效能对比图Fig.5 Comparison of prediction results of RF model and combat effectiveness of anti-ship missile

3.3 梯度提升回归树模型仿真

梯度提升回归树模型将Huber损失函数作为模型残差处理方法以降低样本残差损失，同时为了评估模型优劣，用平均绝对百分误差(MAPE)为评价指标，计算公式为

(22)

式中:ttrue，i为反舰导弹i状态下的作战效能标签值；tpredict,i为梯度提升回归模型预测值。

模型有2个关键参数：学习率和树的深度。通常情况下，随着树的棵数和树的深度的增加，模型能够减小训练误差，但是如果两者数太大，将会导致其泛化能力迅速减弱，模型也会出现过拟合现象导致预测性能降低。因此，通过优化模型的学习率和树的深度将预测误差降到最低。以MAPE为评价指标(数值越小表示预测准确率越好)，学习率和树的深度2个参数的寻优平均分数热图如图6所示。

图6 GBRT模型学习率和树的最大深度平均分数热图Fig.6 Learning rate and maximum depth average fractional heatmap of GBRT model

通过随机搜索寻找最优取值，随机森林模型参数的范围及优选取值如表4所示。

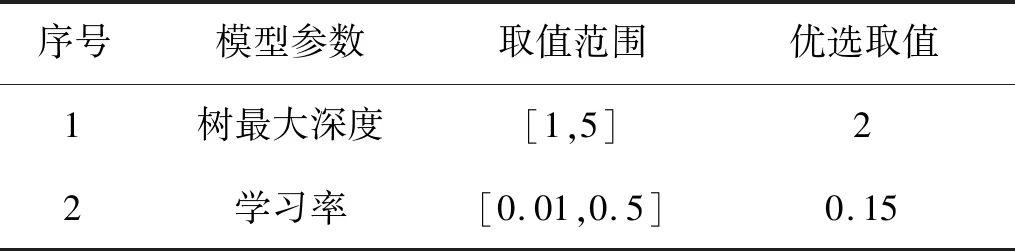
表4 梯度提升回归树模型参数选择Table 4 Parameter selection of GBRT model

仿真结果表明，与改进ADC评估模型求出的反舰导弹作战效能E相比较，在输入特征值后，梯度提升回归树模型对测试集的预测准确率为97%。两者对比如图7所示，其中红线为改进ADC评估模型求出的反舰导弹作战效能标签值，绿线为梯度提升回归树的模型预测值。

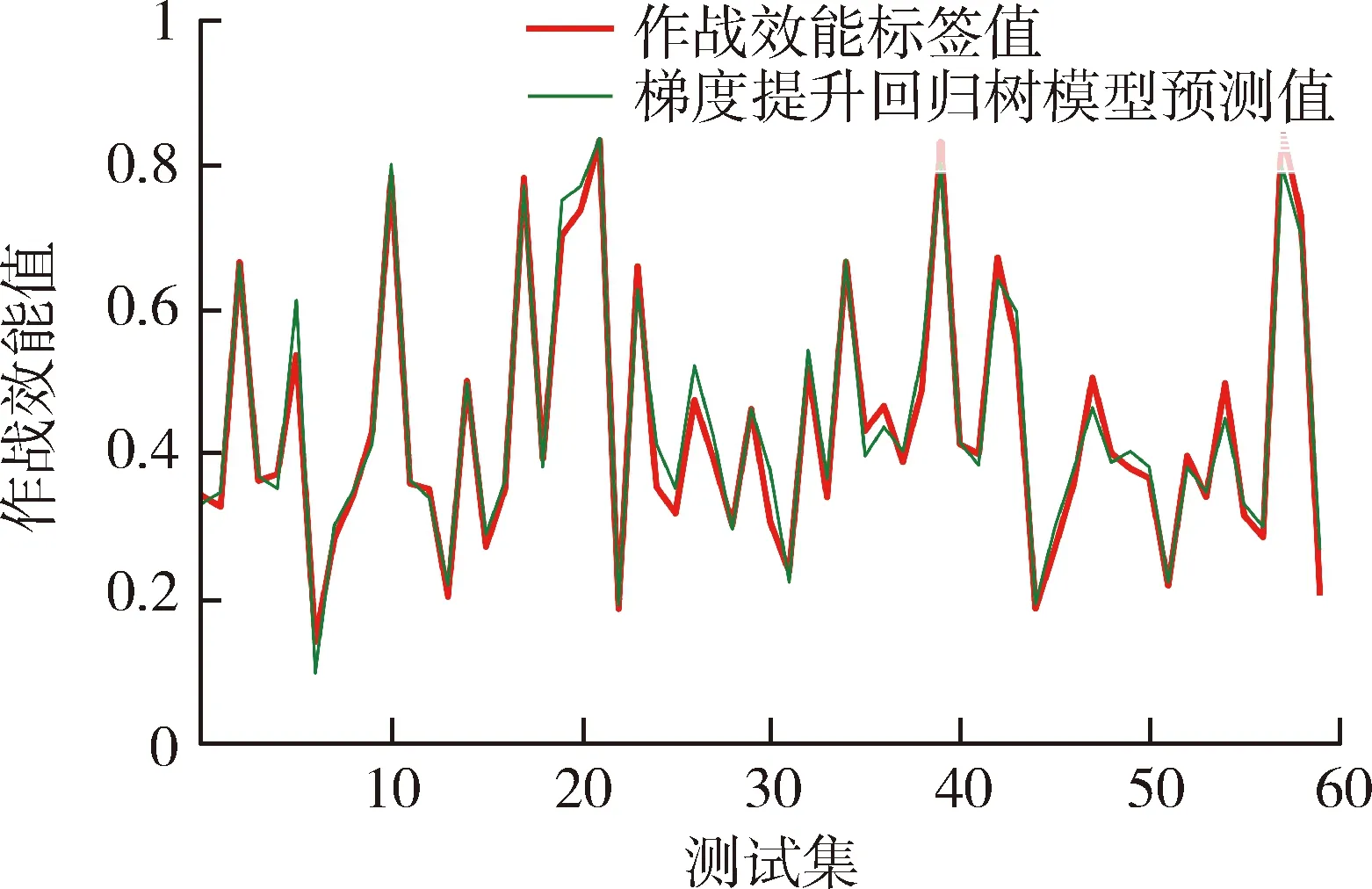
图7 梯度提升回归树模型预测结果与 反舰导弹作战效能对比图Fig.7 Comparison of prediction results of GBRT model and combat effectiveness of anti-ship missile

4 结束语

本文针对实战化条件下反舰导弹武器系统作战效能评估特点，在作战效能评估指标体系基础上建立了随机森林和梯度提升回归树2种决策树集成模型。采用240组数据样本对该模型进行了仿真测试，通过与改进ADC评估模型的对比分析，决策树集成方法的评估预测准确率分别达到了92%和97%，证明了2种方法在反舰导弹作战效能评估研究上的可行性，并且实施过程简单高效，较大程度规避主观经验，容易推广到其他武器系统效能评估中，具有一定的应用价值。