差分电感的建模与仿真及其在振荡器电路中的应用
李超 宛操 朱浩慎 薛泉
0 引言
随着CMOS工艺的发展,集成电路朝着高集成、低功耗的方向发展,并使得CMOS工艺更加广泛地应用在毫米波集成电路中.在毫米波集成电路中,电感的作用往往无法被取代.作为关键器件之一的电感,在电路中主要起到了调谐、匹配、滤波,以及扼流圈等功能.然而,对于一些特殊性能的电感,无法简单地通过工艺库获取参数,借助第三方的电磁仿真软件得到的S参数文件尽管精度高,但在具体电路中会降低仿真速度并且影响电路收敛性.因此需要对电感进行建模,尽可能使用简单的集总元件去等效某个频段的电感特性,包括感值与品质因数Q,借此可以更高效地进行集成电路的设计与仿真.
为了对电感特性进行描述,国内外学者提出了各种类型的等效电感模型.1998年Yue等[1]提出了最简单的电感π模型,该模型可以在电感发生自谐振之前有效地模拟电感的电磁特性.随着频率的升高,多种寄生效应导致π模型无法模拟这些寄生.因此,文献[2]于2012年提出双π模型,双π模型能够更为广泛地模拟电感中存在的趋肤效应与邻近效应带来的寄生,能更好地适应高频环境.为了更准确地提取模型参数,Yang等[3]于2014年提出了T模型,相比于π模型,T模型能够在自谐振频率之后也能有效地模拟电感的性能,但相应的结构也变得更加复杂.在近几年,国际上关于片上电感的研究逐渐成熟[4-6],模型也逐渐完善,但是它们都是将电感单独孤立出去作为一个模块进行建模与仿真的,结合了具体电路的电感模型仍需进一步进行建模与优化.
为了解决上述问题,本文提出了能够适配于振荡器电路的电感建模方法,该方法所构建出来的电感模型能够更好地与振荡器电路相适配,并且能够改善仿真的收敛性,同时加快电路的仿真速度.在接下来的章节中,首先将建立电感的一般模型,分析模型的感值以及Q值与多个电磁(EM)仿真软件的误差.其次,结合具体的振荡器电路,分析优化电感中关键节点的寄生参数,构建适配于振荡器的具体电感模型,通过比较电感模型、EM仿真结果以及实测结果对振荡器性能产生的误差,分析模型的优缺点.最后对本文提出的电感建模方法进行归纳与总结,分析其在不同电路中的应用方法.
1 CMOS片上电感分析
一般情况下,代工厂会针对不同尺寸的电感提供一套统一的电感模型,但是该模型往往只适用于较低频段,毫米波频段产生的寄生往往是模型库里的电感无法模拟的.因此,对于一个带有中心抽头的差分电感,本文设计了如图1所示的模型.图2为实际电感版图.
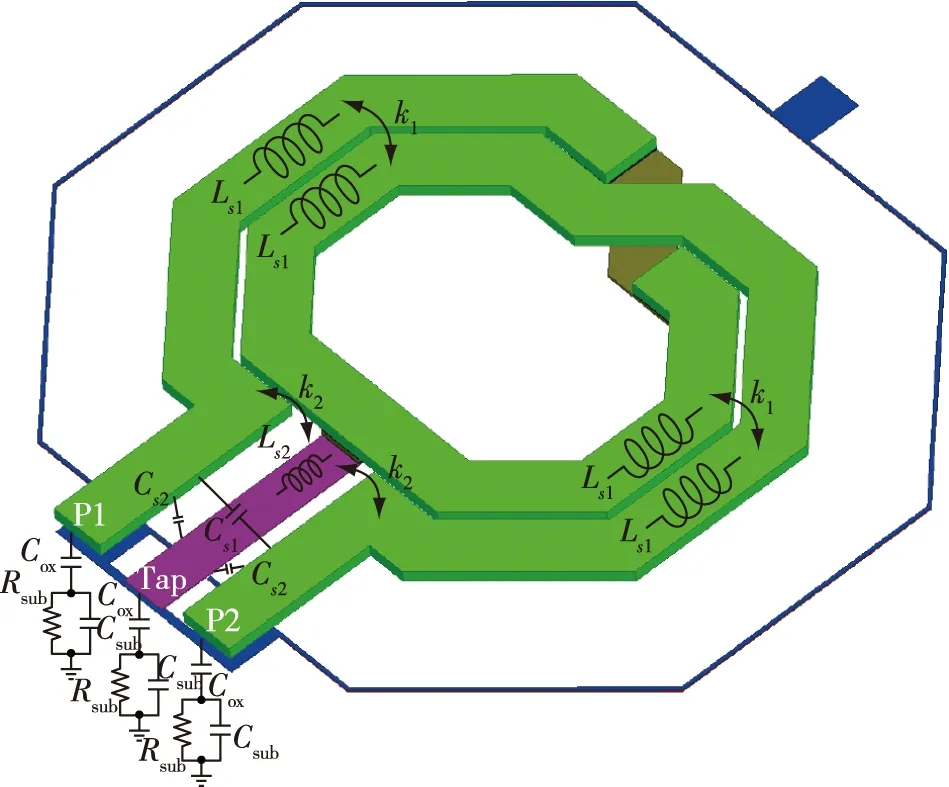
图2 差分电感三维版图Fig.2 The 3D layout of differential inductor
图1、图2中Ls1是差分电感的一半等效电感,Rs1是其对应的等效电阻,表示金属的串联损耗.两个相互缠绕的Ls1会相互耦合,形成耦合系数k1,如图 2所示.由于中心抽头的存在,会产生Ls2的等效电感,Rs2是其对应的串联损耗,同时Ls2会与Ls1形成耦合,产生耦合系数k2.随着工作频率的增加,电感Lp1和Lp2以及对应的损耗电阻Rp1和Rp2表示趋肤效应、邻近效应与衬底涡流带来的影响[7].另外,P1、P2和Tap三个端口之间会形成耦合电容Cs1和Cs2,该电容会随着电感间距的增大而减小.整个电感会在氧化物层形成电容,我们将其等效到P1、P2和Tap处,容值为Cox.另外,以硅为衬底的工艺下还会在衬底层中形成到地的电容Csub以及其寄生电容Rsub.
为了验证模型的准确性,我们选取一组八边形中心抽头差分电感为例子,其中间距S=2 μm,线宽W=15 μm,圈数N=2,半径R分别为20、25和30 μm,仿真其P1、P2、Tap三个端口的S参数.根据式(1)—(4)[8],可以通过S参数获取电感感值Ldiff与品质因数Qdiff.
(1)
(2)
(3)
(4)
利用HFSS电磁仿真软件对电感进行仿真,并利用仿真得到的S参数进行模型的参数提取,将提取得到的参数代入模型,并对模型进行S参数仿真,最后通过式(1)—(4)可以得到如图3—5所示的对比结果.对比结果显示,集总电路模型与仿真结果相当吻合,电感值和Q值的偏差都在5%以内.
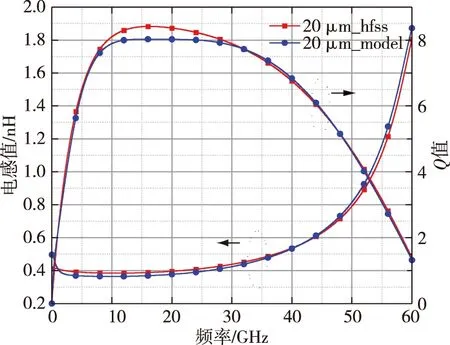
图3 基于HFSS仿真与模型拟合下R=20 μm电感感值和Q值比较Fig.3 Comparison of inductance and Q between HFSS simulation and model under R=20 μm
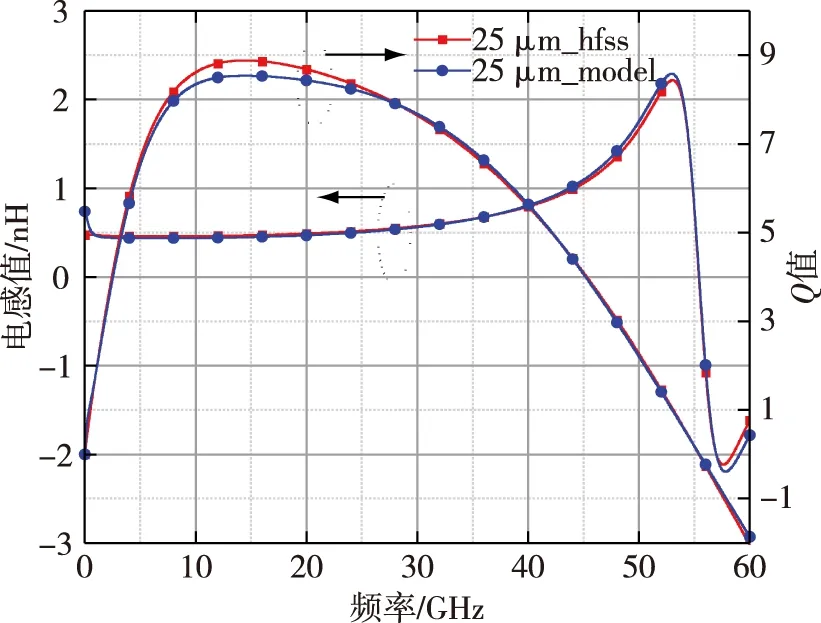
图4 基于HFSS仿真与模型拟合下R=25 μm电感感值和Q值比较Fig.4 Comparison of inductance and Q between HFSS simulation and model under R=25 μm
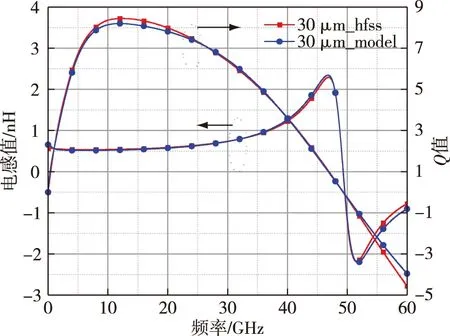
图5 基于HFSS仿真与模型拟合下R=30 μm电感感值和Q值比较Fig.5 Comparison of inductance and Q between HFSS simulation and model under R=30 μm
2 改进型片上电感分析
在实际使用中,由于芯片加工厂的要求,往往需要加入金属块进行密度填充,这一部分金属块将增加电感到地的电容.同时,电感的多个输入端口到Pad上的引线会增加电感本身的感值.如果这一部分引线与其他金属线或金属块比较接近,还会增加电感本身的寄生,从而对电感本身的性能造成进一步影响.接下来将详细地分析这部分的影响并对原有模型进行改进.
2.1 金属块对金属线的影响
一般来说,芯片加工对金属密度会有一定的要求,而电感往往不能满足此密度要求,代工厂会在电感区域添加电感识别层,该层用于芯片加工时对电感进行识别,跳过对电感密度的检测.同时由于该识别层的存在,代工厂要求在电感周围添加金属块,这部分金属块往往会增加电感到地的寄生电容.一般来说,电感由顶层金属(例如M9层)构成,周围的金属块从M1层覆盖到M9层,如图 6a所示,当电感通过较高频率的信号时,电感的电磁感应效应增强,导致金属块上产生反方向的涡流,这些涡流会导致能量损耗.根据Q值的定义[9],能量损耗会导致Q值的下降.另外,周围的金属块可以等效成多个电容Ccouple的串联,如图 6b所示,这些等效电容会增加电感到地的寄生电容,导致电感自谐振点的偏移.
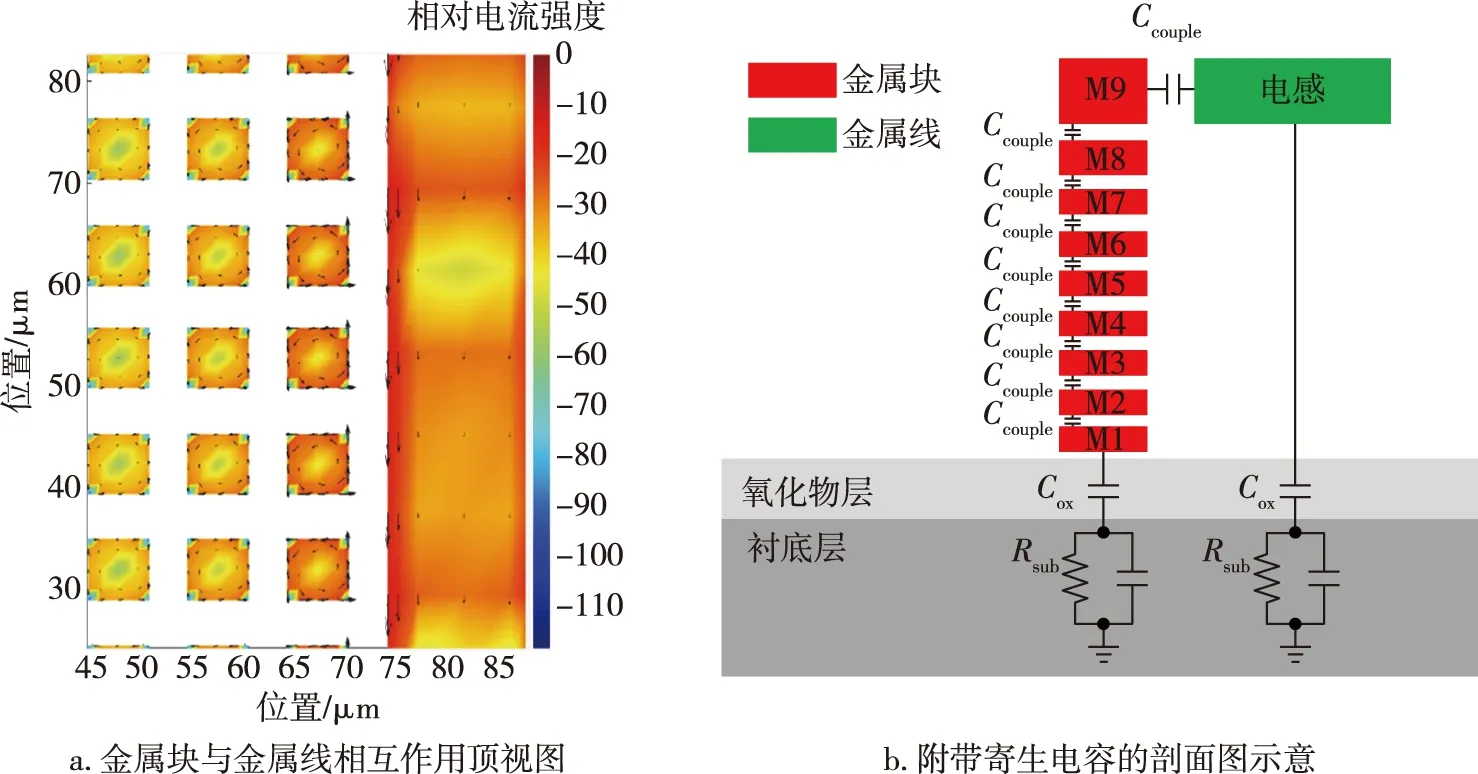
图6 金属块对金属线的影响示意图Fig.6 Schematic diagrams of influence between metal blocks and metal wires (a),and parasitic capacitance (b)
经过上述分析,由金属块引入的寄生电容相互串联到地,最底层的金属块同样会在氧化物层和衬底层形成寄生电容.同时,由于涡流的原因,会导致电感的Q值下降,即可以等效成增大了电感的串联寄生电阻,该电阻的阻值由下降的Q值决定.
2.2 金属线对金属线的影响
由于实际使用的电感往往需要把金属线延伸到所需的位置,这就导致了电感各个参数的变化.同时,在金属线延伸的过程中,如果有其他走线与电感金属线相距较近,高频的电感金属线会与其他走线形成耦合,包括电偶合和磁耦合.因此在实际使用中,需要根据实际情况改进模型,将电感金属线与其他走线的耦合考虑进去.
对于一根高频金属走线,会与其周围靠近的其他金属线产生耦合.先以两根金属走线为例,此时可以分为两种情况,两者平行或垂直,其中平行的情况尽管包含两金属线同层或者不同层的情况,但是这两者产生的耦合原理基本一致,只是耦合大小不同.垂直的情况仅考虑不同层的情况.以下分析这些耦合情况,在图 7a中,金属走线相互平行,相当于两个相互平行的电感,对应的等效图如图7b所示,等效图忽略了衬底的寄生和趋肤效应的影响.其中,L1表示电感走线,L2表示金属线,R1和R2对应于它们的寄生电阻.金属线之间的磁耦合用耦合系数k表示,两者之间的电偶合用电容Cc表示.在实际使用中,若电感走线周围有别的平行金属走线,都可以采用这种模型进行等效,同时要添加对应的衬底和趋肤效应的影响.
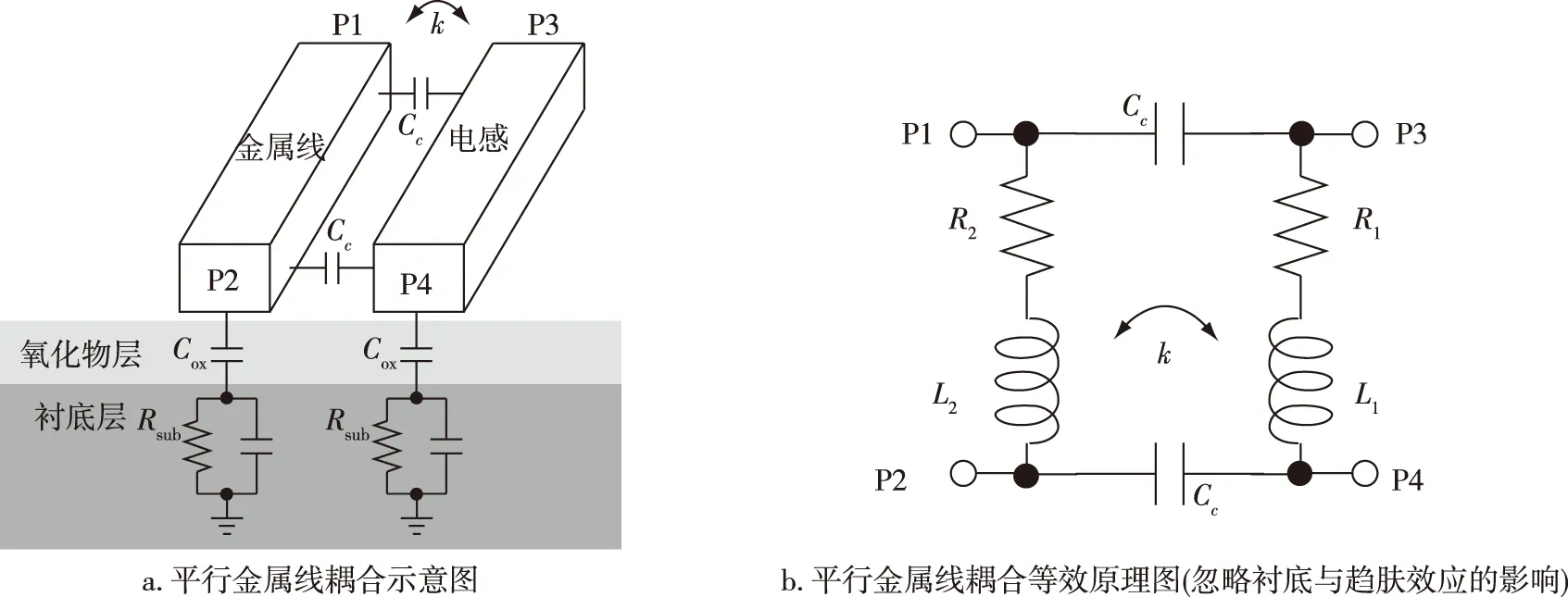
图7 平行金属线示意图Fig.7 Schematic diagrams of parallel metal wires coupling (a),and its equivalent principle (ignoring the influence of substrate and skin effect) (b)
当金属走线与电感走线相互垂直时,如图8a所示,相互垂直的两根金属走线必定处于不同的层中,两者会在重叠处产生较小的电偶合,此处由Cc表示.另外,两者的磁耦合同样用耦合系数k表示.在图8b的等效原理图中,将电感从重叠处拆分成两段电感L1,对应的寄生电阻为R1,中间节点用耦合电容Cc表示两段金属线的电偶合.L2表示金属走线,其对应的寄生电阻为R2.此外L1和L2之间的磁耦合用k表示.
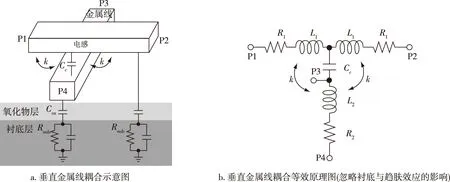
图8 垂直金属线示意图Fig.8 Schematic diagrams of vertical metal wires coupling (a),and its equivalent principle (ignoring the influence of substrate and skin effect) (b)
2.3 改进型电感模型
经过上述分析,将填充密度的金属块和其他金属走线的影响结合实际设计的电感添加到之前的模型中,可以灵活地设计出可以兼容不同结构的电感模型.以TSMC 65 nm工艺为例,本文设计了如图9所示的电感,该电感为了方便测试,在P1和P2端口加入了两个GSG Pad,该Pad自带36 fF的寄生电容.对应的电感芯片照片如图10所示.
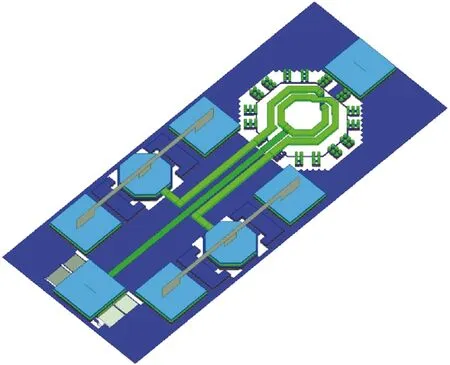
图9 三维电感模型Fig.9 Three dimensional inductor model

图10 电感芯片照片Fig.10 Picture of inductor chip
根据图9所设计的电感,考虑引入的填充密度金属块,以及Tap端引出的长走线,在图1的基础上,建立了如图11所示的电感模型.其中,Cpad表示GSG Pad引入的寄生电容,Cc1表示金属块到地的寄生电容,Rs1和Rs2在涡流的影响下将增大,以模拟Q值的下降.三个端口的长金属走线产生的影响不仅增加了Ls1和Ls2的大小,同时增强了耦合系数k1和k2,因此无需增加额外的器件.经过HFSS仿真与模型的参数提取,我们得到了电感模型的各个器件参数,结合式(1)—(4),可以拟合出电感模型的感值和Q值,并与实际测试结果进行对比.在实际测试中,我们使用了RNS ZVA67矢量网络分析仪进行S参数的测试,将Tap接地,将P1和P2接入仪器得到对应的S11、S12、S21、S22,同样结合式(1)—(4),得到了实际测试结果,模型结果与实测结果如图12所示.从结果可以看出,拟合的结果跟测试的结果基本保持一致,其中拟合的Q值略微大于测试的结果的原因是测试的时候某些仪器损耗没有在拟合中考虑进去.
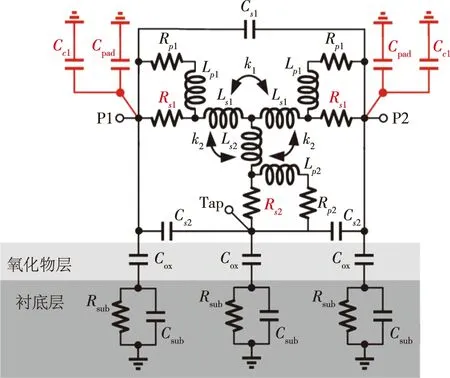
图11 改进型电感模型Fig.11 Modified inductor model

图12 电感模型与测试结果比较Fig.12 Inductance comparison between the model and test result
3 电感模型在振荡器电路的应用
只有将电感放到实际电路中进行建模才能验证电感模型的有效性,本章节通过对应用于压控振荡器(VCO)电路的电感进行分析,建立与实际版图相结合的电感模型,并用HFSS仿真和进行参数提取,将得到的器件参数带入电感集总模型.我们使用该模型进行VCO调谐范围、相位噪声等性能的仿真,并与实际测试结果进行对比.
3.1 振荡器电路版图设计
为了验证电感模型在实际电路中的有效性与准确性,本节以一个最为简单的交叉耦合VCO为例,设计了如图13所示的原理图,并画出了对应的版图,如图14所示.其中,L1、C1和C2构成谐振器,决定了VCO的输出频率.M1和M2管子构成交叉耦合对,提供复阻抗以便VCO产生振荡信号.M3、L2、C3和M4、L3、C4分别构成左右两个缓冲器以便输出信号的测试.在版图中,电感L1为中心抽头差分电感,L2和L3是单端电感,它们处于缓冲器之中,其感值和Q值对VCO输出频率不会有很大的影响.因此,在接下来的内容中,我们将重点分析电感L1.
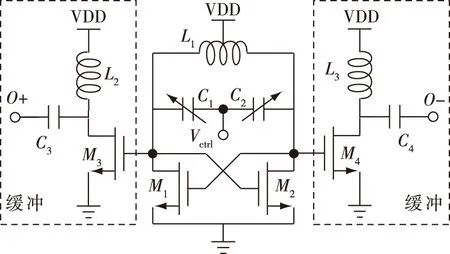
图13 VCO原理图Fig.13 Schematic of VCO

图14 VCO芯片版图Fig.14 Layout of VCO
3.2 振荡器电感模型建立与参数提取
分析图14的版图,提取出谐振电感,如图15红色部分都为中心抽头电感及其延伸出去的部分,其中P1和P2端口延伸到谐振器下方的交叉耦合MOS管,并且中间连接了缓存MOS管和变容管C1和C2,这些都会引入寄生电容.另外,Tap的引出会与其他金属线形成耦合,导致Tap与其他金属走线形成互感.因此,基于前面章节对金属块和金属线之间关系的分析,我们对当前版图的电感,设计了全新的电感模型,如图16所示.其中Cc1是金属块引入的寄生电容,L3为P1和P3引出到MOS和变容管的金属线,Cc2为L3金属线上对应的寄生电容.由于涡流的影响以及L3的存在,R1相较于之前的值要大,一方面用于模拟Q值的下降,另一方面模拟L3的寄生电阻.L4为Tap端引出的长金属线,其对应的寄生电阻添加到R2中,从图16可以看出其会与周围的另一根金属线L5相互产生耦合,耦合系数为k3,电偶合为Cc3.将这部分电感提取出来并使用HFSS进行电磁仿真,对得到的S参数文件进行参数提取,得到对应的集总参数模型的器件参数.利用集总参数模型替代S参数文件进行VCO的相关性能仿真.
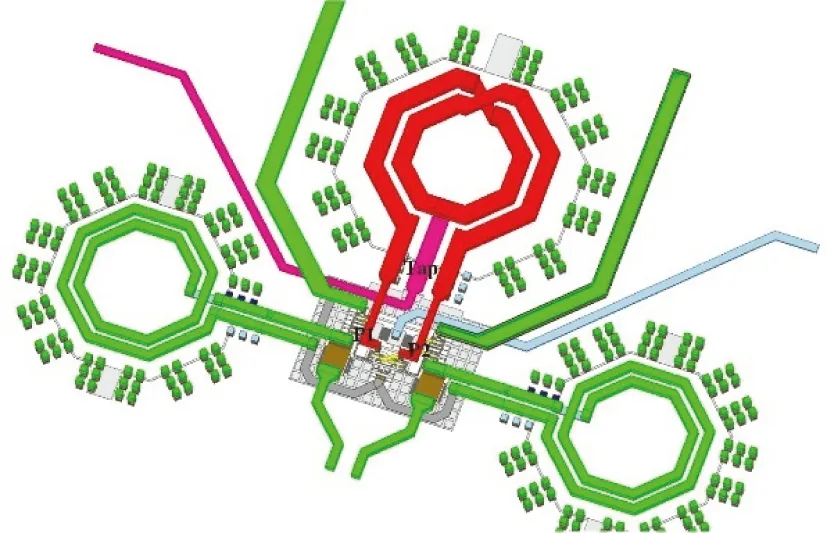
图15 版图上谐振电感Fig.15 Layout of resonance inductor

图16 基于版图的电感模型Fig.16 Layout-based inductor model
3.3 仿真结果与实测结果的比较
最终验证的VCO使用TSMC 65 nm的工艺,对应的芯片照片如图14所示.使用顶层金属M9层设计电感,以降低电感的损耗以及提高电感的Q值.芯片的核心面积为0.235 mm×0.360 mm.为了测试输出信号,在信号的输出端加入开漏MOS管连接到片外,并在片外通过Bias-T偏置连接到R&S FSW67频谱仪上.使用VDD为1 V的电压源进行供电,并赋予Vctrl0~1.2 V变化的电压,测试输出频率和相位噪声的变化范围,同时将该范围与集总参数模型仿真结果进行比较,如图17所示,结果表明,使用集总参数模型仿真得到的结果与测试结果基本吻合.
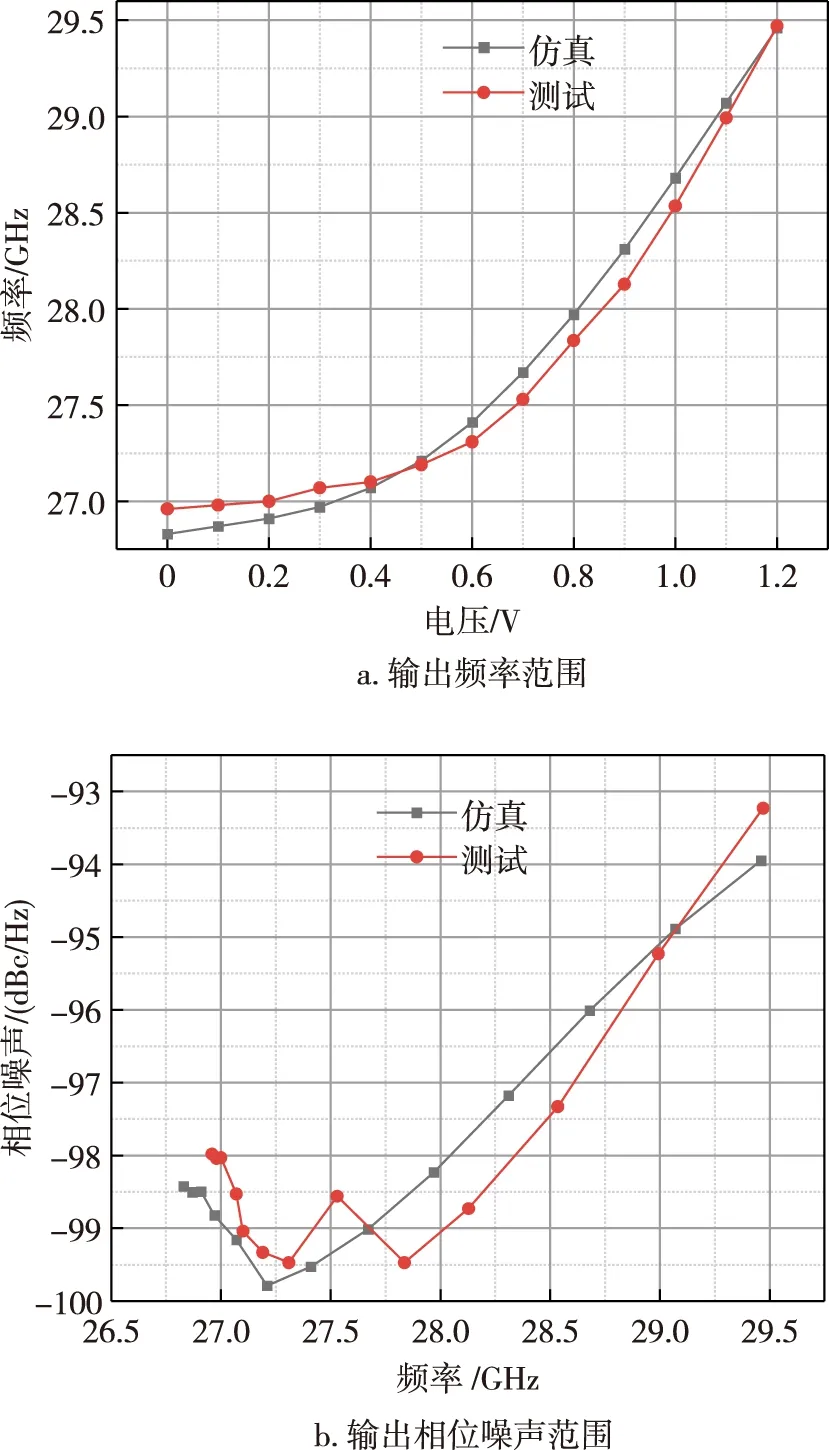
图17 仿真结果与测试结果比较Fig.17 Comparison between simulation and test results,frequency range (a),and phase noise (b)
4 总结
本文提出了中心抽头差分电感的等效模型.该模型可以结合实际的版图进行建模,能更好地反映电感版图的物理特征.同时,分析了金属块和金属线对电感的影响,并构建了对应的集总模型.在TSMC 65 nm的工艺下,测试了一个单独的电感,结果表明测试结果跟模型结果基本保持一致.将本文提出的构建电感模型的方法应用于VCO电路之中,设计了VCO谐振器中的中心抽头差分电感,流片测试的结果也验证了电感模型的有效性,其调谐范围与相位噪声基本吻合.

