基于改进混合蛙跳算法的个性化旅游路线推荐
申晓宁 王森林 吴俊潮 仇友辉 张磊 李常峰 王玉芳
0 引言
随着人们生活水平的不断提高,越来越多的人会在闲暇之余选择外出旅游,也因此带动了不少城市第三产业的发展.而外出旅游到一个陌生的地方,如果不提前做好旅游路线的规划,可能会导致在旅行过程中出现费时、费钱等体验差的问题.同时,不同的旅游人群对于历史人文、自然景观、美食购物等有不同的需求.因此,如何针对旅游者的个性需求,规划适合的旅游路线,并为其选择合适的出行方式以提高在旅游过程中的体验,对于民众生活质量的提升具有重要意义[1].
旅游路线规划问题是基于经典的旅行商问题演化而来的,其主要思想是将候选城市的景点按照一定的规则进行组合优化.目前国内外对此问题的研究颇为广泛,针对此问题还提出了一些其他的改进算法,如动态规划算法[2]、模拟退火算法[3]、蚁群算法[4]等.杨萍[5]的研究表明,路线规划者最终考虑的目标主要分为两种,一是成本最低,二是收益最大;明勇等[6]以城市垃圾回收路线总路径、车辆总费用和惩罚成本为目标建立了城市生活垃圾回收路径规划的数学模型,并对基本混合蛙跳算法进行了改进,提出了一种能够有效实现城市垃圾回收的路线规划方法;黄于欣等[7]针对多景点景区路径规划问题提出了一种改进的蚁群算法,有效地避免了算法陷入局部最优,使得算法快速收敛;杨晓敏[8]通过对蚁群算法的参数调整和改进,成功实现了黄河金三角旅游路线的规划;陈春朝等[9]针对蛙跳算法迭代速度慢的问题提出了改进混合蛙跳算法,提高了算法的进化速度和精度,并将其用于优化人工势场的参数以提高路径规划能力;Shiripour等[10]根据旅行人口对链接时间的影响和在网络上的分布方式,提出了混合整数非线性规划模型,并提出了求解模型的遗传算法(GA),解决了规划出行时间灵活的人行道网络问题;Reyes-Rubiano等[11]为了更好地指导搜索过程,通过在可变邻域搜索框架内集成偏向随机化策略,提出了一种基于元启发式的方法,用于解决同时考虑了经济、环境和社会维度的多站点车辆路径问题;Snchez-Oro等[12]提出了一种通用的变量邻域搜索算法,寻求使路线总数、总旅行成本和最长路线最小化的开放式车辆路径问题解决方案.本文在以上研究的基础上,建立个性化旅游路线推荐问题的优化模型,并针对该模型的特点,提出一种基于改进混合蛙跳算法的个性化旅游路线推荐方法.通过调整可控精度在算法接近结束时扩大搜索范围,以降低遗漏更优解的风险;通过在劣解的改进过程中增加筛选准则以强化局部搜索能力,从而在保持精度的情况下尽可能加快收敛速度;通过引入惩罚因子大幅度降低异常解的适应度,使其在子群的更新中被淘汰,以及时处理异常解,提高算法的运算速度.以南京三日游为旅游路线优化问题的实例,对所提模型和方法进行了仿真验证.
1 基本蛙跳算法原理
混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)是由Eusuff和Lansey为解决组合优化问题于2003年提出的一种全新的元启发式群体进化算法,具有高效的计算性能和优良的全局搜索能力[13].SFLA的思想是:在一片湿地中生活着一群青蛙,湿地内离散地分布着许多石头,青蛙通过在不同的石头上跳跃以找到食物较多的地方.每只青蛙可以定义为问题的一个解.将湿地的整个青蛙群体分为不同的子群体.在子群体中的每个个体有自己的文化,既影响其他个体,也受其他个体的影响,在子群内个体之间通过文化的交流实现信息的交换,执行局部搜索策略.每个个体随着子群体的进化而进化.每个子群体也有着自己的文化,当子群体进化到一定阶段以后,各个子群体再进行混洗,实现子群体间思想的交流(全局信息交换),直到满足所设置的终止条件后算法停止.基本混合蛙跳算法SFLA的伪代码如算法1所示:
算法1基本蛙跳算法SFLA
输入:子群个数M,子群内个体数量I,种群个体总数量I×M,子群更新次数N,混合迭代次数G,当前迭代次数g.
输出:全局最优解.
a) 初始化种群,计算个体目标函数值;
b) forg=1 toGdo
c) 对所有个体按目标函数值从小到大排序并分成M个子群;∥假设为最小化问题,目标值越小,则个体越优;
d) 根据排序与分组结果记录当前全局最优解Xg、各子群局部最优解Xb、局部最差解Xw;
e) fori=1 toNdo
f)Xwnew=Xw+λ(Xb-Xw)∥λ为0~1的随机数;
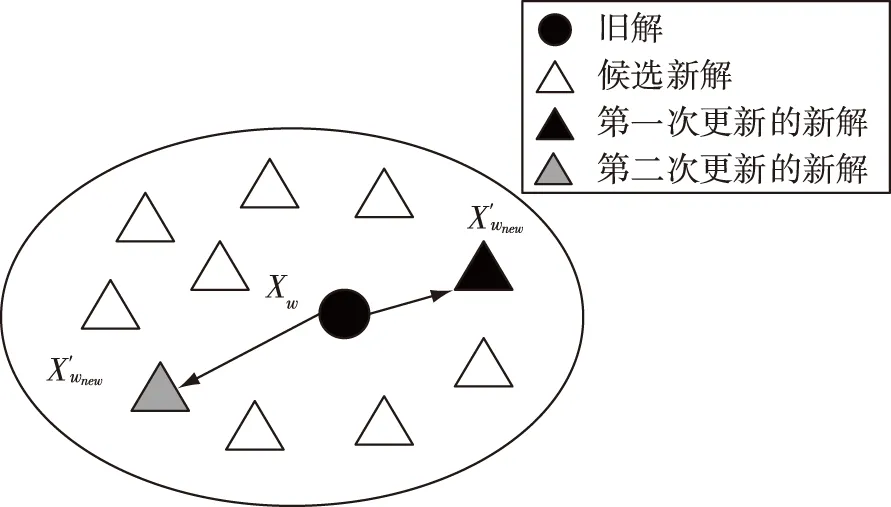
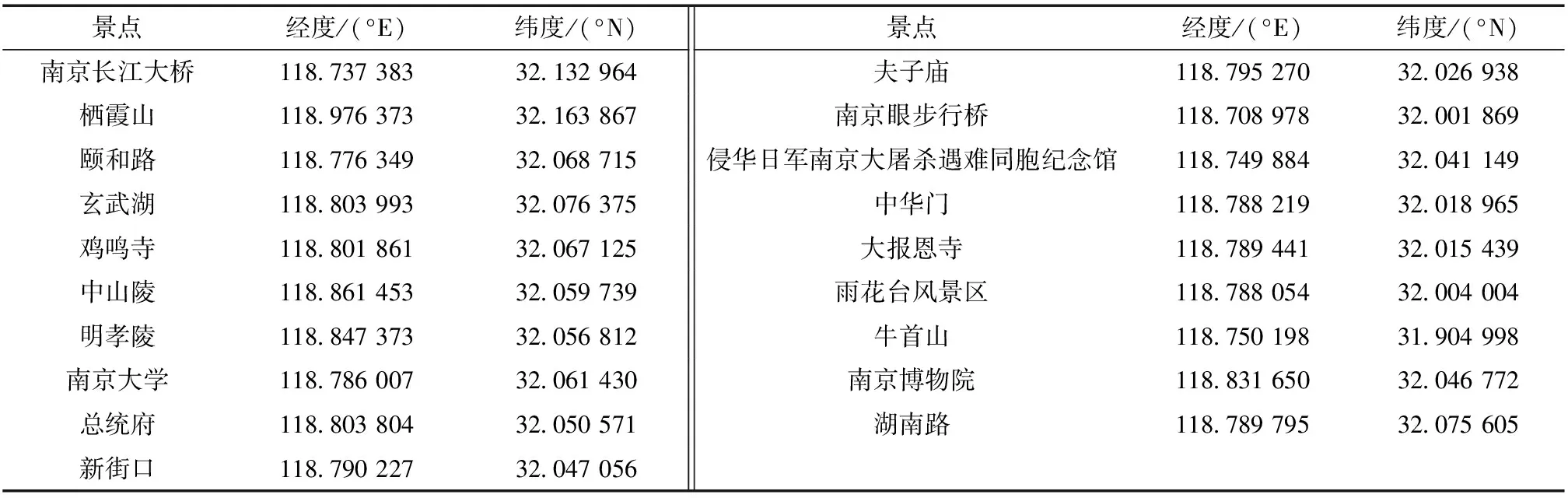
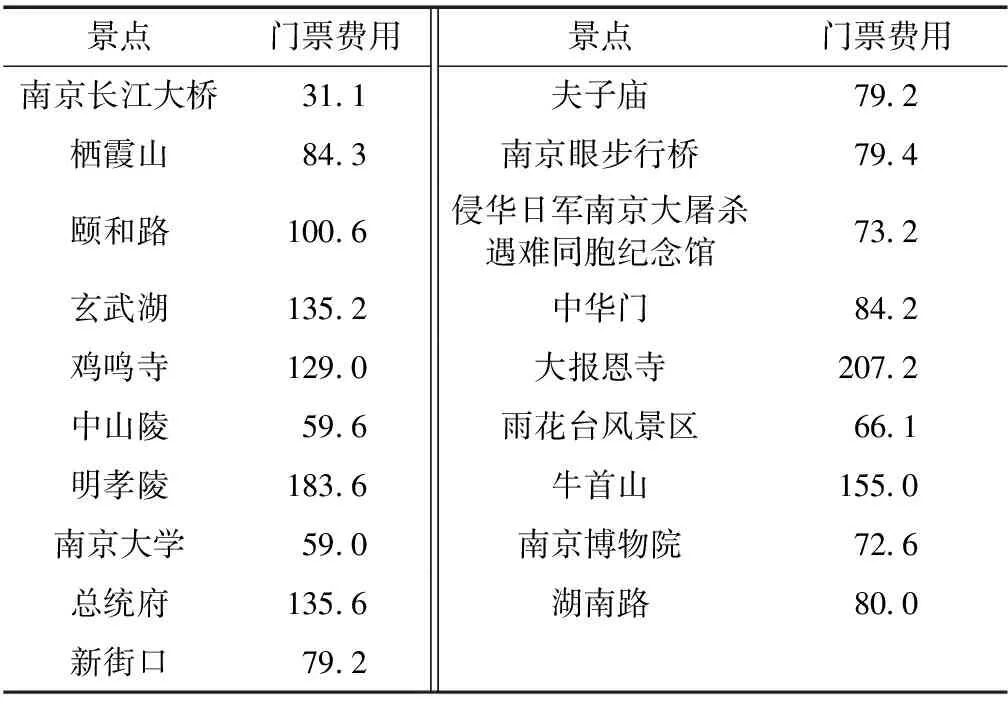
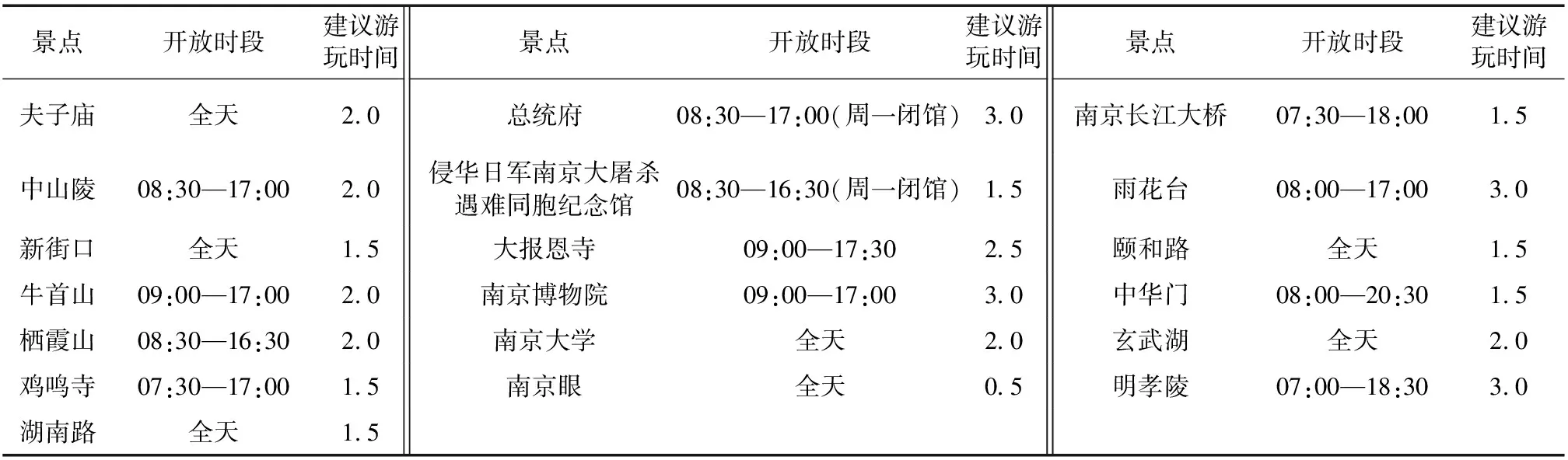
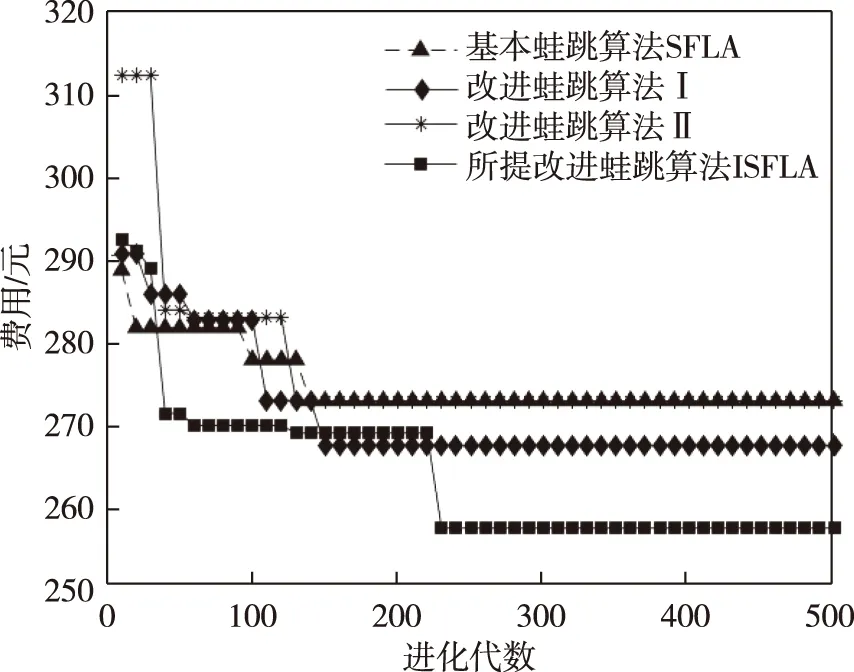
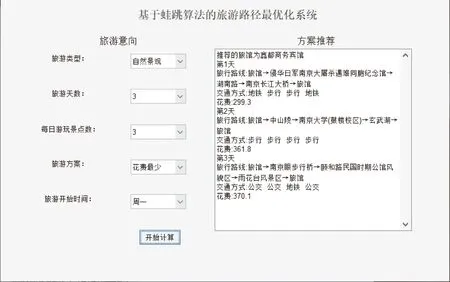
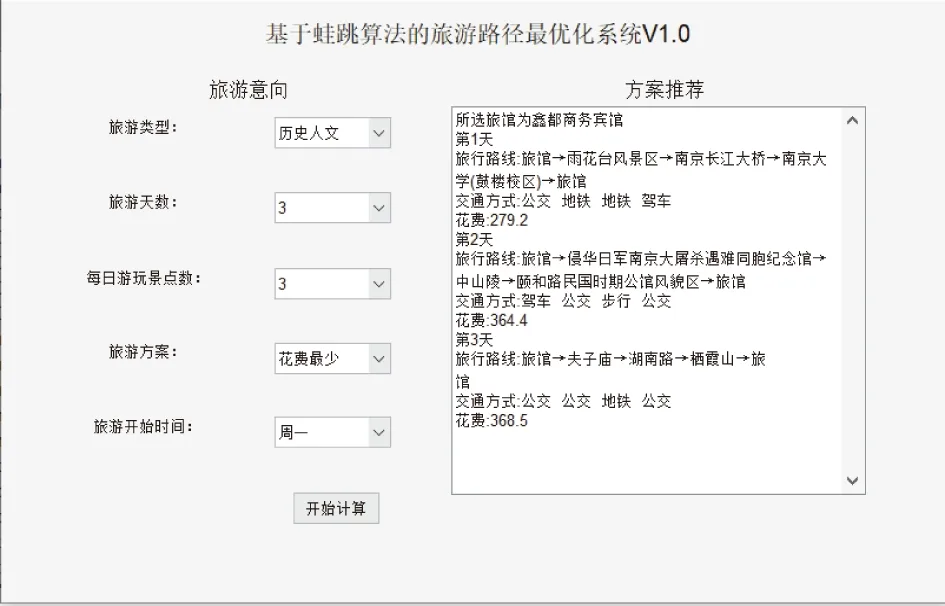
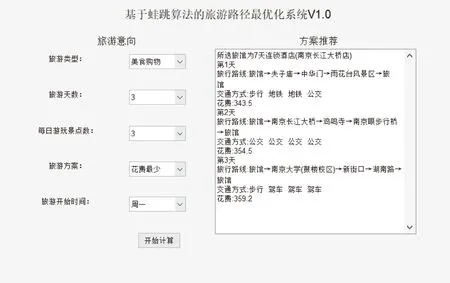
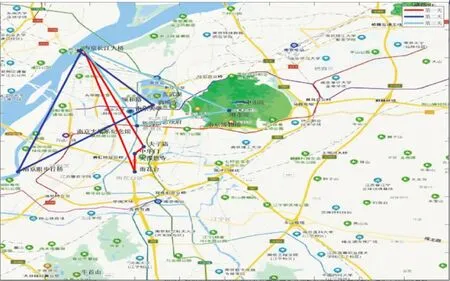
g) ifF(Xwnew) h)Xw=Xwnew i) elseX′wnew=Xw+λ(Xg-Xw)∥λ为0~1的随机数; j) end if k) ifF(X′wnew) l)Xw=X′wnew m) else n) 随机产生新解代替Xw; o) end if p) 对组内个体按目标值从小到大排序,重新确定局部最优解Xb,局部最差解Xw; q) end for r) 将所有个体混洗,记录全局最优个体Xg; s) end for 其中,分组是将所有个体按目标值大小进行升序排序后,将种群分成了M个子群,每个子群中个体数量为I.按照混合蛙跳算法的分组规则将每个个体分配至各自的子群.分配规则如式(1)与表1所示. 表1 子群分配表 Race(k)=[rank(k),rank(M+k), rank(2M+k),…,rank((I-1)M+k)], (1) 式中,Race(k)表示编号为k的子群,rank(k)表示排序在第k位的个体,k=1,2,…,M. 注:rank(·)为各排名对应的个体. 为了便于模型描述,本文做出如下假设: 1)假设旅游者从自己所在地到达旅游目的城市的相关影响因素不在路线规划考虑之内,模型选取的出发点为旅游者所在旅游目的城市的任意景点或者酒店. 2)根据文献[14],假设旅游者在旅游过程中只能选择步行、公交、地铁、驾车4种出行方式,且若选中某个景点,该景点只能被游览一次. 3)假设以旅游期间内的日平均费用最少作为优化目标. 4)根据文献[15],假设所有景点开放时间为8:00—18:00,共计10 h,则每日耗时T应满足T≤10. 5)假设游玩的最大天数为dmax,每天最多游玩nd个景点,其中d=1,2,…,dmax. 6) 在选定某一个酒店作为起点后,每天都以该酒店作为旅游路线的起点与终点. 7) 假设用户的个性化设置体现在选择偏好的旅游类型,如自然景观游、历史人文游、美食购物游等.设共有n种可选旅游类型,每种旅游类型对应的景点集合为O1,O2,…,On.满足用户的个性化需求是指:为其规划出的旅游路线中,至少包含一个符合该用户偏好旅游类型的景点. 个性化旅游路线推荐问题的数学模型可以描述为:在用户的个性化设置下,找出最优决策向量X=[r,Pb],其中r为地点标号组成的向量,表示旅游路径,Pb为交通方式标号组成的向量,表示交通方式的选择,以最小化如下目标: minF=f(X), (2) f(X)=con(r)+con(Pb), (3) (4) (5) (6) (7) (8) 设用户通过个性化设置选择了第j种旅游类型,该类型对应的景点集合为Oj,则满足约束条件: s.t. T(d)≤10, 1≤d≤dmax, (9) r(1)∩r(2)∩…∩r(d)∩…∩r(dmax)= {p0}, (10) [r(1)∪r(2)∪…∪r(d)∪…∪r(dmax)]∩ Oj≠∅, (11) 式(9)—(11)为约束条件.式(9)由假设4给出.式(10)由假设6给出,每日旅游路线的起点都是同一个酒店,且每个景点最多只能被游览一次,因此不同日期的路线交集仅包含p0.式(11)由假设7给出,表示为用户规划出的旅游路线中,至少包含一个景点对应的旅游类型与该用户设置的偏好旅游类型一致. 本文采用改进混合蛙跳算法对用户旅行的路径和交通方式的选择进行组合优化.通过改进混合蛙跳算法不断迭代进化以期获得符合用户需求的最佳旅游路线与交通方式.所提算法采用调整可控精度、新增筛选准则和异常解的处理三种改进策略. 本模型的解由路径r与交通方式Pb组成,算法采用十进制整数编码的方式对个体进行编码.对于n个候选景点{s1,s2,s3,…,sn},为便于表示,依次标记为S={1,2,3,…,n},对于4种交通方式{公交,地铁,驾车,步行},依次标记为W={1,2,3,4},则旅游天数为dmax,第d天游玩景点数量为nd的个体X的编码方式如图1所示. 图1 个体X编码方式示意图Fig.1 Schematic diagram of individual X coding mode 基本蛙跳算法中,种群规模与分组数量这两个参数在进化过程中均保持不变.如果增大种群规模和分组数量,能够使得算法的搜索范围扩大、寻优能力增强,但同时也加大了运算的软硬件资源消耗,运算时间较长.因此,本文为了权衡求解精度与资源消耗及运算时间之间的互斥关系,为混合蛙跳算法设定了一个迭代次数的中间阈值T=fth×G,其中G为算法的总迭代次数,fth为控制结果精度的调节因子.当迭代次数达到T时,在原种群中加入规模与原种群规模相同的新的种群,使搜索范围扩大,该方案的示意图如图2所示. 图2 调整可控精度示意图Fig.2 Schematic diagram of adjusting controllable accuracy 由图2可知,在对初始种群A进行了T次的进化迭代之后得到了种群A(T),此时在种群A(T)中加入与其规模相同的种群B得到了新的种群(A(T)+B).对于新的种群进行(G-T)次的进化后算法达到了终止条件,此时种群(A(T)+B)(G-T)中的最优个体即为混合蛙跳算法搜索到的全局最优个体. 显然,调节因子fth取值越小,种群规模扩大得就越早,搜索范围也就越大,从而使得发现最优解的概率增大.但是过早地进行种群扩大与直接增大初始种群规模是近似等效的,这样做固然可以提高结果精度,但是也会大幅度地降低收敛速度,加大软硬件资源的损耗. 在算法运行到后期时,种群缺乏多样性,且可能已陷入局部最优解,原本的搜索范围不足以搜索到潜在的更优解,于是可以选择在此时扩大搜索范围,以降低遗漏更优解的风险.在本文的仿真实验中,取调节因子f=0.9,即迭代次数中间阈值T=0.9G. 图3 基本蛙跳算法两次个体更新示意图Fig.3 Schematic diagram of two individual updates for basic frog leaping algorithm 图3中黑色圆点表示子群体的局部最差解Xw,黑色三角表示第一次更新产生的新解Xwnew,灰色三角代表第二次更新产生的新解X′wnew,白色三角表示尚未搜索到的候选新解.根据混合蛙跳算法的筛选规则,若Xwnew和X′wnew都比Xw差,则会直接舍去Xw,用搜索空间内的一个随机解替代.这也就意味着,两次更新不仅决定了产生的新解的取舍,也决定了当前解Xw的取舍.在Xwnew和X′wnew都比Xw差的情况下,当舍去Xw后,当前状态下的搜索区域会被产生的随机解的搜索区域替换.与经历过多次搜索更新操作的Xw相比,随机解具有更大的不确定性,以随机解为更新对象的搜索区域在很大概率上会劣于Xw,因此,原混合蛙跳算法仅通过判断适应度大小来决定当前解Xw的取舍,可能会造成具有较大搜索潜力的Xw的丢失. 针对上述问题,本文在基本蛙跳算法的筛选规则中新增了一条:如果在第二次更新后的新解X′wnew仍劣于Xw,则计算X′wnew与Xw之间的欧拉距离(即跳跃步长的幅值)来衡量变化程度,若变化程度大于阈值ε,则说明当前Xw的搜索范围较大,仍采用X′wnew替代Xw;反之舍去,随机产生新解代替当前Xw.特别地,在本模型中取 (12) 其中,D1max=Xb-Xw,D2max=Xg-Xw,它们分别表示第一次和第二次更新中,跳跃步长的最大可能值;‖·‖2表示向量的2范数.所提新增筛选规则的特点是:通过在个体的更新过程中判断实际步长的幅值大小,既可以降低丢失具有较大搜索潜力的Xw的风险,又能够防止算法陷入局部最优.改进混合蛙跳算法筛选准则的伪代码如算法2所示. 算法2改进混合蛙跳算法的筛选准则 输入:当前子群局部最差解Xw,第二次更新后得到新解的X′w. 输出:更新后的解Xw. a) ifF(X′wnew)≥F(Xw) then b) if ‖X′wnew-Xw‖2<εthen c) 在搜索空间里产生随机解Xwnew代替Xw; d) else e)Xw=Xwnew f) end if g) end if 在生成解的过程中,经常会出现重复、交叉等异常解的情况,若是采用强制性的循环来避免异常解的产生会大大增加算法运算时长甚至陷入死循环.为了解决这一系列问题,本文在生成每一个随机个体之后,立即判断其是否为异常解,若为异常解,则用一个数值足够大的惩罚因子ΔC代替其目标值,即 f(Xh)=ΔC. (13) 显然,通过引入惩罚因子后异常解的目标值被赋予了一个较大的惩罚值,使其在后续的子群更新中被淘汰,简化了模型,提高了运算速度. 基于上述3种改进策略,用于求解个性化旅游路线推荐问题的改进混合蛙跳算法ISFLA(Improved Shuffled Frog Leaping Algorithm)的伪代码如算法3所示. 算法3改进蛙跳算法伪代码ISFLA 输入:子群个数M,子群内个体数量I,种群个体总数量I×M,子群更新次数N,混合迭代次数G,当前迭代次数g. 输出:全局最优解. a) 初始化种群,计算个体目标函数值; b) forg=1 toGdo c) ifg==Tthen d) 根据3.2节扩大种群规模; e) end if f) 对所有个体按目标函数值大小排序并分组,根据排序与分组结果记录当前全局最优解Xg、各组局部最优解Xb、局部最差解Xw; g) fori=1 toNdo h)Xwnew=Xw+λ(Xb-Xw)∥λ为0~1的随机数; i) ifF(Xwnew) j)Xw=Xwnew k) else X′wnew=Xw+λ(Xg-Xw) ∥λ为0~1的随机数; l) end if m) ifF(X′wnew) n)Xw=X′wnew o) else 执行算法2; p) end if q) 对每组个体按目标函数值大小排序,重新确定局部最优解Xb,局部最差解Xw; r) end for s) 将所有个体混洗,记录全局最优个体Xg; t) end for 本文实验以南京游为例建立数据集.搜集南京周边的19个热门景点数据,假设旅游时长为3 d,每天游玩3个景点.通过百度地图搜集目标地点的数据,每组数据包括坐标、名称、景区的开放时间、景区的门票价格、不同出行方式所需的时间和费用以及对应的食宿价格.表2—4分别列出了各景点经纬度、门票费用及游玩时间.由于版面限制,费用和消耗时间的数据不在此列出.以历史人文、自然景观、美食购物作为3种个性化旅游类别.对各景点的分类如下:历史人文={南京长江大桥,颐和路,鸡鸣寺,中山陵,明孝陵,夫子庙,总统府,侵华日军南京大屠杀遇难同胞纪念馆,中华门,大报恩寺,雨花台风景区,牛首山,南京博物院};自然景观={南京长江大桥,栖霞山,玄武湖,中山陵,南京眼步行桥,中华门,雨花台风景区,牛首山};美食购物={新街口,夫子庙,湖南路}. 表2 各景点经纬度 在CPU为Intel(R) Core(TM) i7-7700HQ 2.8 GHz、内存8 GB、WINDOWS 10系统上使用Matlab 2016a进行仿真实验. 实验中的参数取值如下:全局混合迭代次数、初始子群数量、子群内个体数量、种群总规模、子群更新次数、结果精确度的调节因子.为验证所提策略的有效性,分别使用基本蛙跳算法SFLA(算法1)、改进蛙跳算法Ⅰ(SFLA+调整可控精度+异常解的处理)、改进蛙跳算法Ⅱ(SFLA+新增筛选准则+异常解的处理)以及所提改进蛙跳算法ISFLA(SFLA+调整可控精度+新增筛选准则+异常解的处理,即算法3)求解个性化旅游路线推荐问题的数学模型,4种算法分别独立地运行30次,求取它们在30次运行中求得的最少费用的最佳值、均值和方差,比较结果如表5所示. 表3 各景点门票费用 通过观察表5中各算法的运行结果可知,在引入了改进策略后,算法的性能得到了一定程度的提高.与基本蛙跳算法SFLA相比,改进蛙跳算法Ⅰ求得的最少费用均值有所减少,方差也有所降低.这是由于改进蛙跳算法Ⅰ引入了控制结果精度的调节因子,当迭代次数达到设定的中间阈值时,在原种群中加入规模与原种群规模相同的新种群,从而使得搜索范围扩大,群体的多样性增强,有利于增强算法的全局搜索能力.改进蛙跳算法Ⅱ求得的最少费用均值也优于SFLA.原因是在基本混合蛙跳算法的筛选规则中,如果两个新解都比旧解差,则会直接舍去旧解,这就导致在舍去了旧解后,当前状态下的候选新解也会被舍去掉很大一部分甚至是全部.而在本文所提筛选规则中,个体在更新时,跳动的实际步长为最大步长乘以一个[0,1]内的随机数,通过判断实际步长的幅值大小可以很好地降低丢失具有较大潜力旧解的风险,能够防止陷入局部最优.从表5的结果可以看出,本文所提算法ISFLA在同时引入调整可控精度、新增筛选准则及异常解的处理策略后,结合了3个改进措施的优点,使得求得的最少费用的最佳值、均值和方差都得到改善,搜索结果也较SFLA和仅引入部分改进策略的改进算法Ⅰ和Ⅱ更加精确,且结果分布的离散程度更小,说明所提算法ISFLA搜索的稳定性更强. 表4 各景点游玩时间 表5 算法改进前后结果对比 利用显著度水平为0.05的秩和检验法将上述改进蛙跳算法Ⅰ、改进蛙跳算法Ⅱ、ISFLA与基本蛙跳算法SFLA在30次运行中的结果进行了统计测试,结果如表6所示.其中“+”表示相应算法的搜索结果显著优于基本蛙跳算法,“=”表示两者无显著差异,“-”表示显著劣于基本蛙跳算法. 表6 秩和检验结果 通过观察表6的统计测试结果可知,在引入新增筛选准则后,改进蛙跳算法Ⅱ与基本蛙跳算法得到的结果无显著差异,而加入调整可控精度策略的改进蛙跳算法Ⅰ以及所提改进蛙跳算法ISFLA的求解结果均显著优于基本蛙跳算法,进一步说明本文所提改进策略是可行而有效的. 图4给出了4种对比算法的收敛曲线.由图4可见,当总的迭代次数相同时,对于仅引入调整可控精度策略的改进算法Ⅰ,虽然它搜索到的结果优于基本蛙跳算法SFLA,但是其收敛速度相较于SFLA并没有明显的提升;对于仅引入新增筛选准则的改进蛙跳算法Ⅱ,虽然它对最优解精度的改进并不明显,但是它能够以较快的速度收敛;对于同时引入调整可控精度策略和新增筛选准则的所提算法ISFLA,它将改进策略的优点有机地结合,既具有较快的收敛速度,也能够跳出局部极值,获得了更高的求解精度,算法的全局搜索性能得到了大幅度地提升. 图4 算法收敛曲线对比Fig.4 Comparison of convergence curves 由图4还可以看出,当引入改进策略后,所提改进算法ISFLA的收敛速度较SFLA有小幅度降低,其主要原因是在ISFLA的求解过程中,为了避免陷入局部最优,在进化到一定程度时扩大了种群的搜索范围.然而,与SFLA相比,ISFLA能够收敛到精度更优的解,显著提高了算法的求解效率. 进一步,将模型与相应的个性化旅游设置相结合,以花费最少为目标进行优化时得出自然景观、历史人文、美食购物的路线规划如图5—10所示. 从图5—10可以看出,当旅游者选择游览3 d且每天游览3个景点,以费用最低为优化目标时,自然景观、历史人文、美食购物3种个性化旅游方式下各需总花费1 031.2、1 012.1和1 057.2元,ISFLA推荐出的路线能够较好地满足用户的个性需求. 图5 选择自然景观游且以费用最少为优化目标的推荐路线Fig.5 Recommended routes for natural landscape tour with least spending 图6 选择自然景观游且以费用最少为优化目标的轨迹地图Fig.6 Trajectory map for natural landscape tour with least spending 图7 选择历史人文游且以费用最少为优化目标的推荐路线Fig.7 Recommended routes for historical & cultural tour with least spending 图8 选择历史人文游且以费用最少为优化目标的轨迹地图Fig.8 Trajectory map for historical & cultural tour with least spending 图9 选择美食购物游且以费用最少为优化目标的推荐路线Fig.9 Recommended routes for food & shopping tour with least spending 图10 选择美食购物游且以费用最少为优化目标的轨迹地图Fig.10 Trajectory map for food & shopping tour with least spending 本文针对旅游路线个性化推荐问题,设计了一种改进的混合蛙跳算法.通过调整可控精度,新增筛选准则和即时处理异常解来增加群体多样性、降低遗漏最优解风险,强化了局部搜索能力,提高了算法的求解精度.以南京游作为实例,采用改进混合蛙跳算法进行求解,并根据用户的个性选择推荐出了具体的出行方案,在一定程度上为旅游者的出行提供了参考.以多次运行中的最佳值、均值和方差作为测度,验证了不同改进策略的有效性.实验结果表明,在求解精度方面,所提改进算法相较于基本的蛙跳算法有了显著的提升.然而,本文算法也存在着不足,例如本文采用的是单目标优化,而现实生活中旅游者可能有多个旅游需求需要同时优化,如何高效求解个性化旅游路线推荐的多目标优化问题,将是下一步的研究方向.
2 数学模型建立
2.1 数学模型假设
2.2 个性化旅游路线推荐问题的数学模型
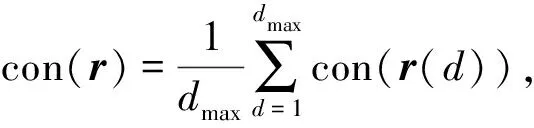


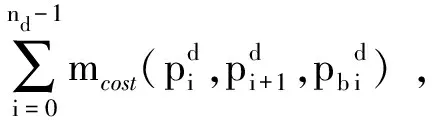

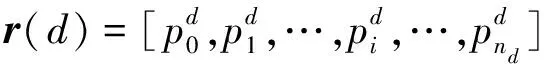
3 求解个性化旅游路线推荐问题的改进混合蛙跳算法
3.1 个体的编码方式

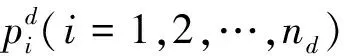
3.2 调整可控精度

3.3 新增筛选准则

3.4 异常解的处理
3.5 改进算法的实现
4 仿真实验
4.1 数据集的建立
4.2 实验结果与分析




5 总结

