面向估计性能的双通道带宽分配策略研究

彭志荣 赵瞩华 陈惠珍 李伟雄 陈相德

0 引言

网络化控制系统(NCSs)将网络空间和物理空间联系起来,使控制器、执行器、传感器等系统组件之间的信号传输以网络通信的方式实现，这能极大地简化系统布线、优化产品构造,因此NCSs在工业控制等领域得到了广泛应用[1-3]．在实际控制中,因带宽受限,以及传输协议、网络流量等因素的影响,系统组件间的信号传输存在时滞．由于时滞具有未知性、随机性、时变性,使得系统的分析与设计变得复杂．为了解决时滞现象所带来的问题,针对离散时间域,本文考虑将系统建模为具有多个模态并且各模态间存在一定转移概率的随机系统,即Markov跳变系统[4-5]．将Markov跳变系统应用于网络化控制,已成为许多学者研究的课题．文献[6]将网络引起的随机延迟建模为Markov链,然后将所得的闭环系统转换为Markov跳变线性系统,在此模型的基础上,提出了不确定NCSs鲁棒有限时间随机稳定的充分条件;文献[7]用隐Markov模型描述了系统和控制器之间出现的异步现象,针对Markov跳变系统解决了异步无源控制问题；文献[8]研究了具有通信限制和环境干扰的网络化控制H∞输出跟踪控制问题,将随机时间延迟和数据包丢失分别描述为两个随机Markov链．

网络通信将众多孤立的设备通过网络联系起来,信号在数据链路中传输,实现信息的互通．近十几年来,网络通信技术快速发展,从城市到乡村几乎都有网络覆盖,网络通信已成为人们生产生活中至关重要的一部分．现有的网络通信方式多种多样,传统互联网通信包括Wi-Fi传输、以太网通信，移动空中网有GPRS无线通信、NB-IOT通信、4G通信等[9-10]．文献[11]利用Wi-Fi设备中可访问的细粒度通道状态信息的相位和幅度的特点,设计室内跌倒检测系统;文献[12]分析了窄带物联网NB-IOT可以以三种模式进行部署,并介绍了NB-IOT的设计规范;文献[13]分析了第五代移动通信技术的引入带来的移动通信运行架构的转变．尽管网络通信技术已蓬勃发展,但是随着人们对传输数据量需求的不断增加，以及对传输速率的要求不断提升,仍然需要改善和革新．

本文使用双通道带宽分配策略进行传输,可以将有限的带宽灵活地分配于两个通道,充分利用信道容量;每个通道在各自的谐振频率处传输效率最高,因此可以对两个通道做带宽分配,根据实际负载大小、传输距离、数据量等因素选择使用合适的通道进行传输．

本文结构如下:第1节描述了离散时间Markov时滞系统的系统模型、双通道量化传输的方案以及估计器的设计;第2节建立了使时变估计误差系统满足H∞性能的充分条件,通过将递归矩阵不等式转化为线性递归矩阵不等式,得出了估计器的增益矩阵设计的方法;第3节给出实例验证了所设计的系统;第4节为总结．

注1本文中：Rn表示n维欧几里得空间;Rn×m表示n行m列的实数矩阵集；上标“T”和“-1”分别表示矩阵的转置和逆;P>0(P∈Rn×m)表示P是实对称正定矩阵；I表示相应阶数的单位矩阵；*表示对称矩阵中相应对称的元素；diag{…}表示对角矩阵；E(x(k))表示x(k)的期望．

1 问题描述及系统建模

1.1 系统模型

考虑如下的离散时间马尔可夫时滞系统:

(1)

其中x(k)=[x1,x2,…,xn]T∈Rn是系统状态向量,y(k)∈Rm是系统的测量输出,z(k)∈Rp是系统待估计信号,ω(k)∈Rq是外部扰动输入并且属于空间L2∈[0,∞),f(·)是非线性函数并且满足假设1,d(k)是未知的但满足d1≤d(k)≤d2的正整数时滞,{θ(k),k∈Z+}是一个离散的马尔可夫链,它的取值范围是一个有限状态集合S={1,2,…,N}．假定系统整个转移概率矩阵都是已知的,并用Π=[πij]i,j∈S来表示,其中从k时刻所处模态i转移到k+1时刻所处的模态j的概率用πij=Pr(θ(k+1))=j|θ(k)=i≥0,∀i,j∈S,k∈Z+表示．矩阵Aθ(k),Bθ(k),Cθ(k),Dθ(k),Eθ(k)和Lθ(k)是已知的并具有合适维度的系数矩阵．

1.2 双通道量化传输

由于带宽是有限的,使用量化器可以在一定程度上克服带宽约束,充分利用信道容量．在离散时间马尔可夫时滞系统的状态估计中,本文更重视小信号,所以采用非均匀的对数量化器,也就是信号幅值小的地方量化等级越多,能够保证小信号的精度．对数量化器定义如下:

yq(k)=Q(y(k)),

(2)

其中Q(y(k))=[q1(y1(k))q2(y2(k)) …

(3)

其中δi=(1-ρi)/(1+ρi)．量化误差ei(k)可以描述为

ei(k)≜qi(yi(k))-yi(k)=Δi(k)yi(k),

(4)

其中Δi(k)∈[-δi,δi],则量化后的信号可以描述为

yq(k)=(I+Δ(k))y(k),

(5)

其中Δ(k)=diag{Δ1(k),Δ2(k),…,Δm(k)}．

传输数据的所需信道容量,与所使用量化器的量化密度有关．量化密度越大,传输的数据就越准确,但需要更多的信道容量．量化密度为ρi时,对数量化器量化后的数据所需容量Cdi如下:

(6)

由于yq(k)=[y1q(k)y2q(k) …ymq(k)]T∈Rm,采用双通道传输,量化传输分为以下两种情况:

情况1m为偶数,通道1传输m/2维的数据,量化密度ρi=ρ1,i∈ψa≜{1,2,…,m/2};通道2传输m/2维的数据,量化密度ρi=ρ2,i∈ψb≜{(m+2)/2,(m+4)/2,…,m}．

情况2m为奇数,通道1传输(m+1)/2维的数据,量化密度ρi=ρ1,i∈ψc≜{1,2,…,(m+1)/2};通道2传输(m-1)/2维的数据,量化密度ρi=ρ2,i∈ψd≜{(m+3)/2,(m+5)/2,…,m}．

由于带宽有限,因此对数量化后总的数据容量应小于或等于限定值,记限定值为C,则

C1Cd1+C2Cd2≤C,

(7)

其中C1,C2分别为通道1、通道2的传输数据量,Cd1,Cd2分别是量化密度为ρ1,ρ2时对数量化器量化后的数据所需容量．

1.3 估计误差系统

考虑如下形式的估计器:

(8)

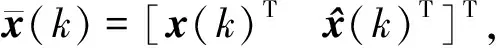
(9)

其中

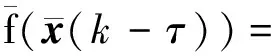
(10)

为了方便对系统做H∞性能分析,引入以下假设、引理和定义．

[fis(a)-fis(b)-F1is(a-b)]T×

[fis(a)-fis(b)-F2is(a-b)]T≤0，

(11)

其中F1is,F2is为已知实矩阵．

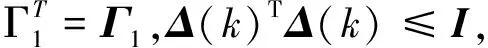
当且仅当存在标量ε>0,使下列不等式成立:

定义1[16]给定一个标量γ>0,如果零初始条件下,下列不等式对于所有非零v(k)均成立,则估计器误差系统具有H∞噪声衰减性能指数γ:

(12)

2 主要结论

2.1 H∞性能分析

本节对估计误差系统(9)的H∞性能进行分析,并给出定理1．首先定义符号:

τ1=diag{τ11,τ11},

τ2=diag{τ12,τ12},

(13)

定理1给定一个标量γ>0,如果存在矩阵:

Pr>0,P1>0,r={1,2,…,N},

ε1=diag{ε11,ε12}∈R2n×2n(ε1≥0),

ε2=diag{ε21,ε22}∈R2n×2n(ε2≥0)

使得下列不等式成立,则估计误差系统(9)满足H∞性能．

(14)

证明引入以下二次函数来分析时变估计误差系统(9)的H∞性能:

(15)

其中Pθ(k)>0,P1>0．

定义θ(k)≜r,θ(k+1)≜s,并且从均值的意义上定义二次函数(15)的差,如下所示:

(16)

将误差系统(9)代入式(16)可得:

(17)

其中:

考虑非线性情况下,根据假设1可得(18)、(19)两个不等式：

(18)

(19)

根据上面得到的两个非线性的不等式条件,不等式(17)满足下面的不等式:

(20)

其中:

将(20)的两边从k=0到k=N求和,可以进一步得到:

(21)

2.2 估计器设计

本节研究基于时变时滞马尔可夫系统的估计器增益,使时变估计误差系统(9)满足H∞性能．

ε1=diag{ε11,ε12}(ε1≥0),

ε2=diag{ε21,ε22}(ε2≥0),

使得下列的不等式成立:

(22)

则时变估计误差系统(9)满足H∞性能．

其中:

Γ2=[εδCr(k) 0 0 0 0 0 0 0εδEr(k)0 0 0]，

Ξ22=-γ2I,

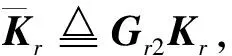
(23)

综合考虑(10)和不等式

(24)

可以得到:

(25)

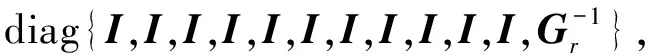
因此,条件(22)使得系统满足:

根据定义1,估计误差系统满足H∞性能．证明完毕．

3 仿真实例

本节将通过一个仿真实例验证所设计的面向估计性能的双通道带宽分配策略的有效性．假设系统中n=5,m=4,Markov模态数N=2,时滞参数d1=1,d2=2,量化器的量化密度范围为ρi∈[0.5,0.95].若要传输4维数据,则根据式(6)可得量化后所需的总信道容量至少为1.908 4,至多为6.396 4．如果带宽上限为4,如何根据双通道量化传输方案分配带宽,即如何调节两个传输通道的量化密度使总信道容量被充分高效的利用、估计误差较小并且系统对外部扰动有较好的抑制能力,成为被考虑的问题．

在本实例中,两个通道的量化密度分别为0.726 4和0.881 3,量化后对应的所需容量分别为0.8和1.2,相应的系数矩阵如下所示:

时变非线性函数如下:

外部扰动为:ω(k)=0.8e-0.1k|sin(k)|,

马尔可夫转移概率矩阵如下:

根据第二节所述的定理并通过Matlab的LMI工具箱,可以得到H∞性能指标为γ=2.890 2,模态1和模态2的估计器增益分别如下:

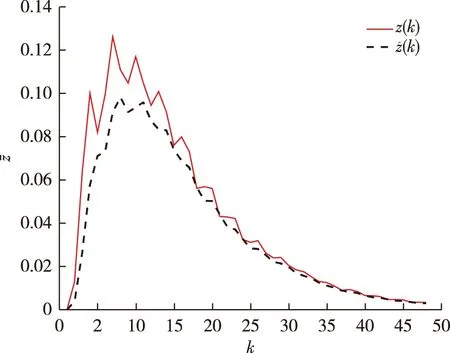
图1 待估计信号z(k)和估计信号Fig.1 Signal to be estimated z(k) and estimated signal

注2本实例仅采用一组量化密度设计出该双通道量化情况下能达到最佳性能的系统．在实际应用中,应根据所传输信号中各部分信号分量幅值的大小设计适合的量化密度,也就是给各个通道分配适合的带宽,从而设计出最佳系统．

4 结论

本文提出了面向估计性能的双通道带宽分配策略．将系统建模为Markov跳变时滞系统,可减小网络化控制系统中时滞现象对信号传输的影响．采用双通道传输策略,提升数据到达率,减少数据包的丢失．双通道量化传输方案可将有限的带宽灵活地分配于两个通道,充分利用信道容量,提升传输效率．本文设计了估计器的增益矩阵以及满足H∞性能的时变估计误差系统,并通过实例验证了所设计系统的有效性．