基于中间估计器的非线性广义马尔可夫跳变系统的故障估计
苏晓明, 石豪达, 包·阿迪亚, 马智慧
(沈阳工业大学 理学院,辽宁 沈阳 110870)
广义系统理论是英国学者Rosenbrock于1974年首次提出并逐渐发展起来的现代控制理论的一个独立分支,其所描述的实际问题在机器人系统、电路系统、网络系统、经济系统等诸多领域均有广泛的应用.在过去的40多年里,许多正常系统中的结论相继被推广到广义系统,广义系统理论的研究也因此进入了一个飞速发展的阶段[1-2].马尔可夫跳变系统是一类具有多种模态的混杂系统,各个模态之间的转移服从马尔可夫过程.在实际工程中,系统的结构和参数通常会发生随机突变,这类突变往往具有马尔可夫过程的特性,因而可以用马尔可夫跳变系统来进行建模[3].近年来,随着马尔可夫跳变系统在实际中的广泛应用以及广义系统理论的不断发展,许多学者开始关注广义马尔可夫跳变系统的稳定性分析与控制问题.容错控制作为控制理论的一个热门研究方向也取得了丰硕的成果[4-5].然而关于故障的确切信息,如其大小和类型通常很难直接获取,需要利用故障估计技术才可以获得详细信息.到目前为止,对于非线性系统已经提出了不同类型的故障估计器:Huang针对具有执行器故障的非线性T-S模糊系统提出了鲁棒观测器[6];Yan设计了一种时滞非线性系统的滑模观测器用于估计未知参数及故障[7-8];Jiang利用李雅普诺夫稳定性理论给出了自适应观测器的设计方法[9].
在以往文献中,对于非线性系统的故障估计已经有了一定的成果,而对于非线性广义马尔可夫跳变系统的故障估计问题研究尚少.本文针对具有全局利普希茨非线性的广义马尔可夫跳变系统,设计了一种基于中间变量的估计器,用于同时估计系统的状态以及故障.然后,构造了误差系统的输入到状态稳定李雅普诺夫函数,证明了误差系统对于故障函数的导函数是输入到状态稳定的,这意味着当故障函数的导函数随着时间收敛于0,误差系统也是渐近收敛的.这不同于现有的故障估计结果[10-11].文献[10-11]的结论表明,当故障函数的导函数有界时,误差系统的状态一致有界,仅当故障函数的导函数恒等于0时,误差系统才是渐近收敛的,但即使一个很小的、有限时间衰减到0的干扰也可能使原本稳定的非线性系统发散.因此,本文的结果相对于现有结果而言,降低了保守性.
1 问题描述和准备知识
考虑如下形式的一类非线性广义马尔可夫跳变系统:
(1)
其中,x(t)∈n,u(t)∈m,y(t)∈p,分别为状态向量,控制输入以及测量出.fa(t)∈r,fs(t)∈q分别为未知的执行器故障和传感器故障.非线性项g(t,x(t))可以表示模型不确定性或扰动,E∈n×n为已知矩阵,并且假设rank(E)=nE≤n.A(r(t)),B(r(t)),C(r(t)),Da(r(t))和Ds(r(t))是依赖于r(t)具有适当维数的已知矩阵,{r(t),t≥0}为取值于有限状态集合S={1,2,…,N}的齐次右连续马尔可夫过程,并且满足如下的模态转移概率矩阵:
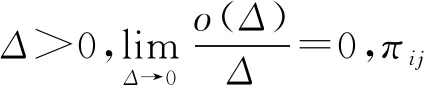
为方便起见,本文中对于每个r(t)=i∈S,矩阵A(r(t)),B(r(t)),C(r(t)),Da(r(t))和Ds(r(t))可简写成Ai,Bi,Ci,Dai和Dsi.那么系统(1)记为如下形式:
(2)
本文对系统做以下假设:
假设 1广义马尔可夫跳变系统(2)对于任意的i∈S,在时间间隔[0,T]内正则且无脉冲.
注1广义系统正则以及无脉冲定义参见文献[12].
假设 2非线性向量g(t,x(t))为已知向量并且对于任意的t≥0,关于x(t)∈n是全局利普希茨的,即满足如下不等式:
|g(t,x1(t))-g(t,x2(t))|≤g|x1(t)-x2(t)|,
假设 3对于任意t≥0,执行器故障fa(t)与传感器故障fs(t)分别满足下面两个不等式:
假设 4Dai和Dsi皆为列满秩矩阵,即:rank(Dai)=r,rank(Dsi)=q.
假设 5对于每个具有非负实部的复数λ都有下式成立:
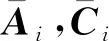
下面给出随机系统输入到状态稳定性以及输入到状态稳定李雅普诺夫函数的定义.

P{|x(t)|≤β(|x0|,t-t0)+γ(‖ut‖)}≥1-ε, ∀t≥t0
(3)
对于任意的初始状态x0和任意局部本质有界的u成立,则称系统(2)是输入到状态稳定的.

ETP=PTE≥0,
(4)
V(x)=xTETPx,
(5)
V(x)f(x,u)≤-κV(x)+γ(|u|)
(6)
成立,则称函数V为这个广义系统的输入到状态稳定李雅普诺夫函数.
注2根据文献[14]主要结果的证明可知,如果系统(2)存在一个输入到状态稳定李雅普诺夫函数,那么该系统是输入到状态稳定的.
如下引理将在主要结果的证明中用到:
引理 1对于向量x∈n和y∈n,以及具有适当维数的实矩阵X和Y,存在标量ε>0,总有如下不等式成立:
2xTXYy≤εxTXXTx+ε-1YyyTYT.
(7)
2 基于中间变量的估计器设计
(8)
其中,
接下来提出一种可以同时估计系统(2)的状态、执行器故障和传感器故障的中间估计器.首先,引入了一个中间变量:
(9)
然后,考虑如下基于中间变量的估计器:
(10)
(11)
(12)
(13)
(14)
(15)
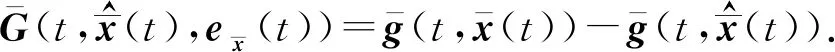
定理1考虑假设1~假设5 成立.给定标量μ>0,ε>0,如果存在矩阵Pi>0(i∈S),Hi和标量δ>0,使得对于每个i∈S,满足下面不等式:
(16)
(17)
其中,
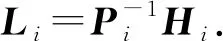
证构造误差系统(14)和误差系统(15)的李雅普诺夫函数为
(18)
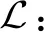

(19)

(20)
根据引理1,有以下不等式成立:
(21)
(22)
(23)
(24)
(25)
将不等式(21)~不等式(25)代入式(20)有:
(26)
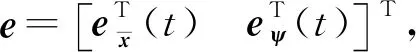
(27)
其中,
(28)
又由李雅普诺夫函数(18)有
(29)
令Ξ2=-Ξ1,当Ξ1<0时,有Ξ2>0.因此,有如下不等式成立:
(30)
其中,
(31)
根据定义2可知,当满足不等式(16)和不等式(17)时,误差系统(14)和误差系统(15)是关于故障函数的导函数为输入到状态稳定的.利用schur补引理可证得Ξ1<0与线性矩阵不等式(17)等价,其中,Hi=PiLi.证毕.
注 3对于初始的μ=μ0,ε=ε0,通过求解线性矩阵不等式(17)可以得到观测增益Li和标量δ.如果不等式(17)不可解,重置μ=μ1,ε=ε1,直到线性矩阵不等式(17)可解为止.
注 4由于输入到状态稳定性蕴含着收敛输入收敛状态的性质[15],所以当故障的导函数随着时间趋于0时,误差系统的状态也是收敛的.这与现有结果是不同的.现有结果表明,当故障函数的导函数有界时,误差系统的状态一致有界,仅当故障函数的导函数恒等于0时,误差系统才是渐近收敛的.但即使一个很小的、有限时间衰减到0的干扰也可能使原本稳定的非线性系统发散.
3 数值算例
考虑如下含有两个模态的非线性广义马尔可夫跳变系统,系数矩阵为
非线性项取为

假定系统中执行器故障与传感器故障的形式如下:
本例的目的是要设计形如式(10)~式(13)的估计器使得误差系统(14)和误差系统(15)对于故障函数的导函数是输入到状态稳定的.假定初始模态r0=1,选取参数ε=1,μ=0.3.利用Matlab中的LMI工具箱,求解线性矩阵不等式(16)和不等式(17),可得观测器增益
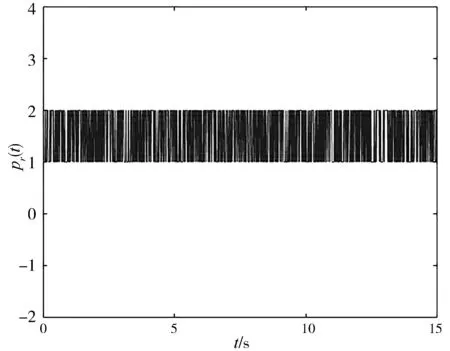
图1 系统(1)的跳变模态

图2 系统状态x1(t)及其估计
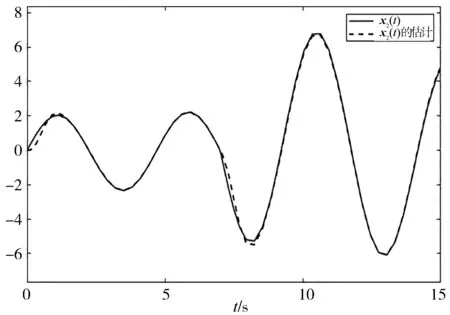
图 3 系统状态x2(t)及其估计

图4 系统状态x3(t)及其估计
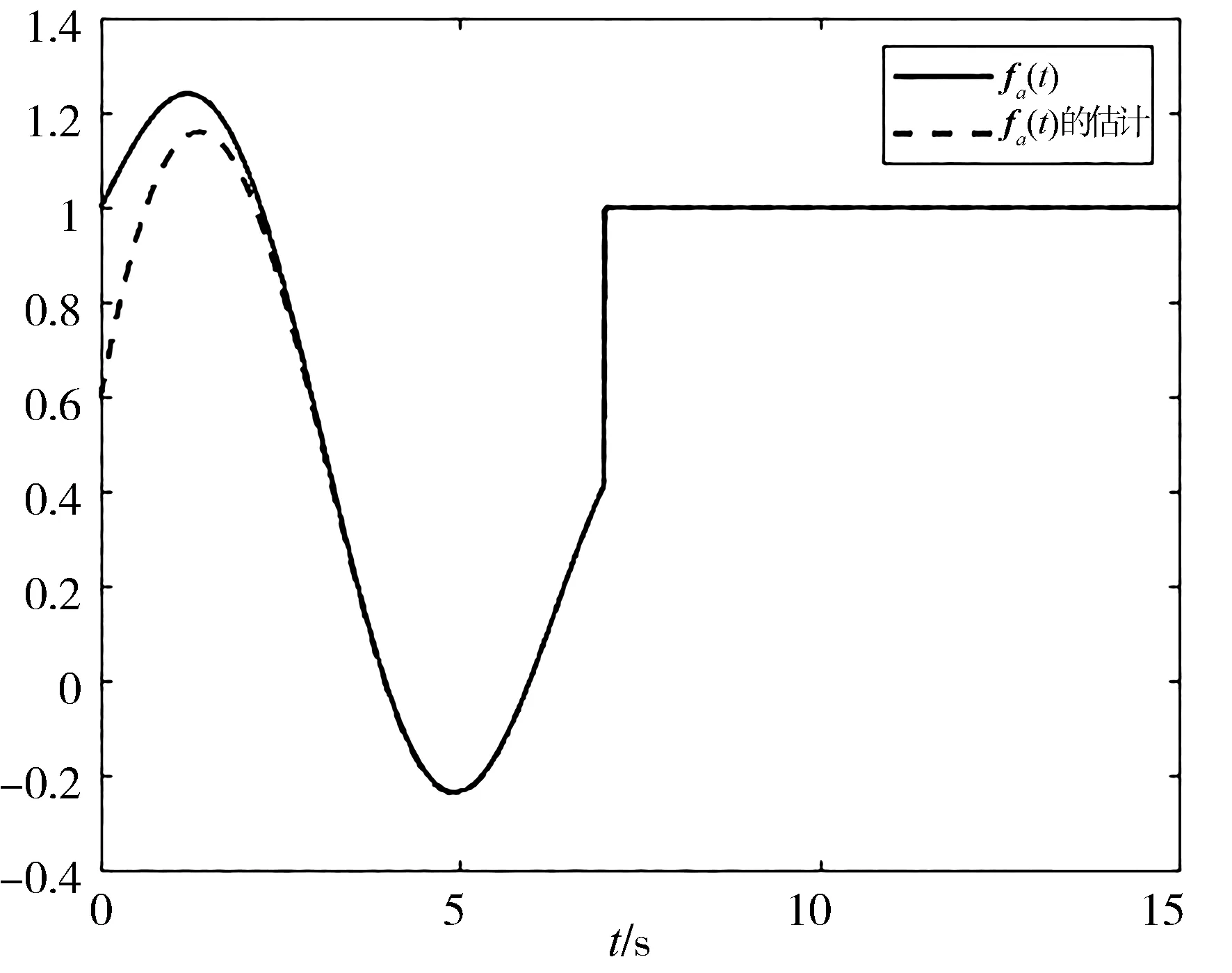
图 5 执行器故障fa(t)及其估计
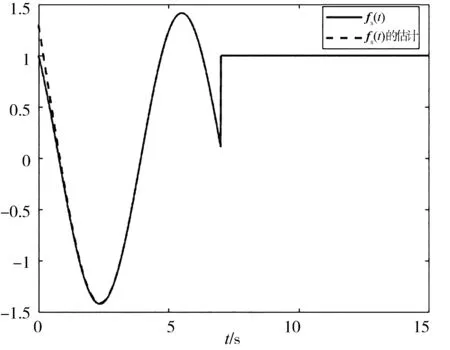
图6 传感器故障fs(t)及其估计
4 结 论
本文研究了一类具有全局利普希茨非线性的广义马尔可夫跳变系统的故障估计问题,考虑了执行器故障和传感器故障并存的情形.设计了基于中间变量的估计器用于估计该系统的状态、执行器故障以及传感器故障.证明了误差系统对于故障函数的导函数是输入到状态稳定的.给出了一个数值算例用以验证该方法的有效性.

