具有黏滞性的相互作用Sharma-Mittal全息暗能量模型的宇宙学演化

吴亚波， 徐东方， 陈博海,3， 董 微

(1.辽宁师范大学 物理与电子技术学院，辽宁 大连 116029；2.厦门外国语学校 高中物理组，福建 厦门 361012； 3.北华航天工业学院 基础科学部，河北 廊坊 065000)

天文观测数据表明[1-2]，宇宙目前正处于加速膨胀阶段.对此，国际上提出各种具有负压强的暗能量模型来解释宇宙晚期加速膨胀[3-5]，其中，宇宙学常数是最简单的暗能量模型[6-8]，该模型的态参数方程(EoS)为wde=-1.虽然宇宙学常数模型成功解释了一些宇宙演化现象，但其仍无法解决巧合性问题和精调问题[7,9-11].于是，人们又陆续提出并研究了诸如Quintessence[12-13]、Phantom[14]、K-essence[15-17]和 Chaplygin gas[18]等暗能量模型.此外，受全息原理[19-21]启发而提出的暗能量模型也被用来解释宇宙的加速膨胀.此类暗能量模型有全息暗能量模型[22](HDE)、Agegraphic暗能量(ADE)模型[23]和Ricci暗能量模型[24]等.

近年来在宇宙学的研究中，还通过使用不同的熵以及全息原理提出了一些新形式的全息暗能量模型，如Renyi全息暗能量(RHDE)模型[25]、Tsallis全息暗能量(THDE)模型[26]和Sharma-Mittal全息暗能量(SMHDE)模型[27].目前RHDE模型和THDE模型已被广泛讨论[28]，但对于SMHDE模型，有关它的黏滞性对宇宙学量演化影响以及几何诊断方法等相关性质目前尚没有讨论过，这正是本文的研究动机和研究内容.

1 Sharma-Mittal全息暗能量模型

Jahromi和Moosavi等通过结合Sharma-Mittal熵和全息原理，提出了一种新形式的全息暗能量模型，称为Sharma-Mittal全息暗能量模型[27].

Sharma-Mittal熵由Sharma和Mittal引入[29]，它是一个双参数熵，定义为

(1)

其中，A=4πL2，L是事件视界，R和δ是两个自由参数.通过对Sharma-Mittal熵的参数R加以适当的限制：R→0及R→1-δ，就可以重新得到Renyi熵和Tsallis熵.当考虑UV截断和IR截断时，可得到暗能量密度为

(2)

因哈勃视界L=1/H，则Sharma-Mittal全息暗能量模型(SMHDE)的暗能量密度可表示为

(3)

其中，c2是常数，R与δ称为模型参数.在本文的讨论中，将模型参数取为R=3 300和δ=-165时，SMHDE模型可以表现出较好的宇宙学行为.

在均匀且各向同性的FRW宇宙中，度规表示为

ds2=-dt2+a2(t)(dr2+r2dΩ2).

(4)

在Sharma-Mittal全息暗能量模型中忽略重子及辐射成分，宇宙仅由暗能量(de)和暗物质(dm)构成.则此模型的Friedmann方程可写为

(5)

(6)

利用方程(6)，可将方程(5)重新表示为

Ωde+Ωdm=1.

(7)

当Sharma-Mittal全息暗能量模型的暗能量和暗物质之间存在相互作用，且不考虑黏滞性(ζ=0)时，它们的能量守恒方程为

(8)

(9)

其中，“.”表示对时间t求导，Qi是暗能量和暗物质之间的相互作用项.相互作用项的选取有多种形式，本文选取Q1=3b2Hρde和Q2=3b2Hρdeρdm/(ρde+ρdm)这两种形式，式中b2是耦合参数.可以注意到，当b2=0时可以退回到无相互作用的情况.用wde=pde/ρde来表示SMHDE模型的态参数(EoS).将方程(5)左右两边对时间t求导，并将结果代入方程(9)中，可以得到

(10)

为使其形式更为简洁，在这里定义Ξ=Gπc2H2(πδ/H2+1)R/δ-(2Ωde-1)(πδ+H2).利用上述方程，减速参数q可写为

(11)

将Sharma-Mittal全息暗能量模型的暗能量密度对时间t求导，从而得到

(12)

联立方程(8)、方程(10)和方程(12)，无相互作用时Sharma-Mittal全息暗能量模型的态参数可表示为

(13)

此外，由方程(10)和方程(12)，其能量密度参数Ωde对lna导数可写为

(14)

其中，“′”表示对lna的导数，i=1,2.

(1)当i=1，即相互作用项为Q1=3b2Hρde时

(15)

(16)

(17)

(2)当i=2，即相互作用项为Q2=3b2Hρdeρdm/(ρde+ρdm)时

(18)

(19)

(20)

根据SN397、BAO以及宇宙微波背景辐射(CMB)等观测数据的限制[30]，本文取Ωde0=0.73，H0=67.此外，值得强调不失一般性，在本文下面的讨论中，将模型参数R和δ取为R=3 300，δ=-165.根据以上各表达式，能描绘出Sharma-Mittal全息暗能量模型中黏滞系数和耦合参数对各宇宙学量(如能量密度参数Ω、减速参数q及态参数wde)演化规律的影响.

图1描述了无黏滞性，且相互作用项分别取Q1=3b2Hρde和Q2=3b2Hρdeρdm/(ρde+ρdm)时，SMHDE模型中耦合参数b2对各宇宙学量演化的影响.从图中可以看出，耦合参数b2对该模型各宇宙学量的影响随相互作用项的不同而不同.在未来(z<0)Q2条件下的各宇宙学量均发生了高度简并，这说明与Q2相比，耦合参数b2对Q1条件下的宇宙学量影响更大些.两种不同相互作用形式下SMHDE模型的密度参数的演化图像都表明，暗能量的占比在逐渐增大，这与目前天文观测相符合.而从两者的态参数随红移z的演化曲线可以得出：Q2条件下SMHDE模型的态参数在未来(z<0)的演化会趋近于ΛCDM模型；两种不同相互作用下的态参数均实现了对Phantom界限(wde=-1)的穿越，且耦合参数b2取值越大，越早实现穿越.从态参数的演化图像也可以看出，两种不同相互作用下的SMHDE模型在未来均不会发生大劈裂.进一步，再纵向对比Q1和Q2条件下SMHDE模型减速参数q演化曲线的特点.由图不难看出，两种不同相互作用下的减速参数q都随着耦合参数b2的增大而减小，且宇宙是由减速膨胀(q>0)演变为加速膨胀(q<0)，但两种不同相互作用下的减速参数q在未来都发生了高度简并，这说明了在未来(z<0)两种不同相互作用形式下的SMHDE模型都对耦合参数b2不敏感.

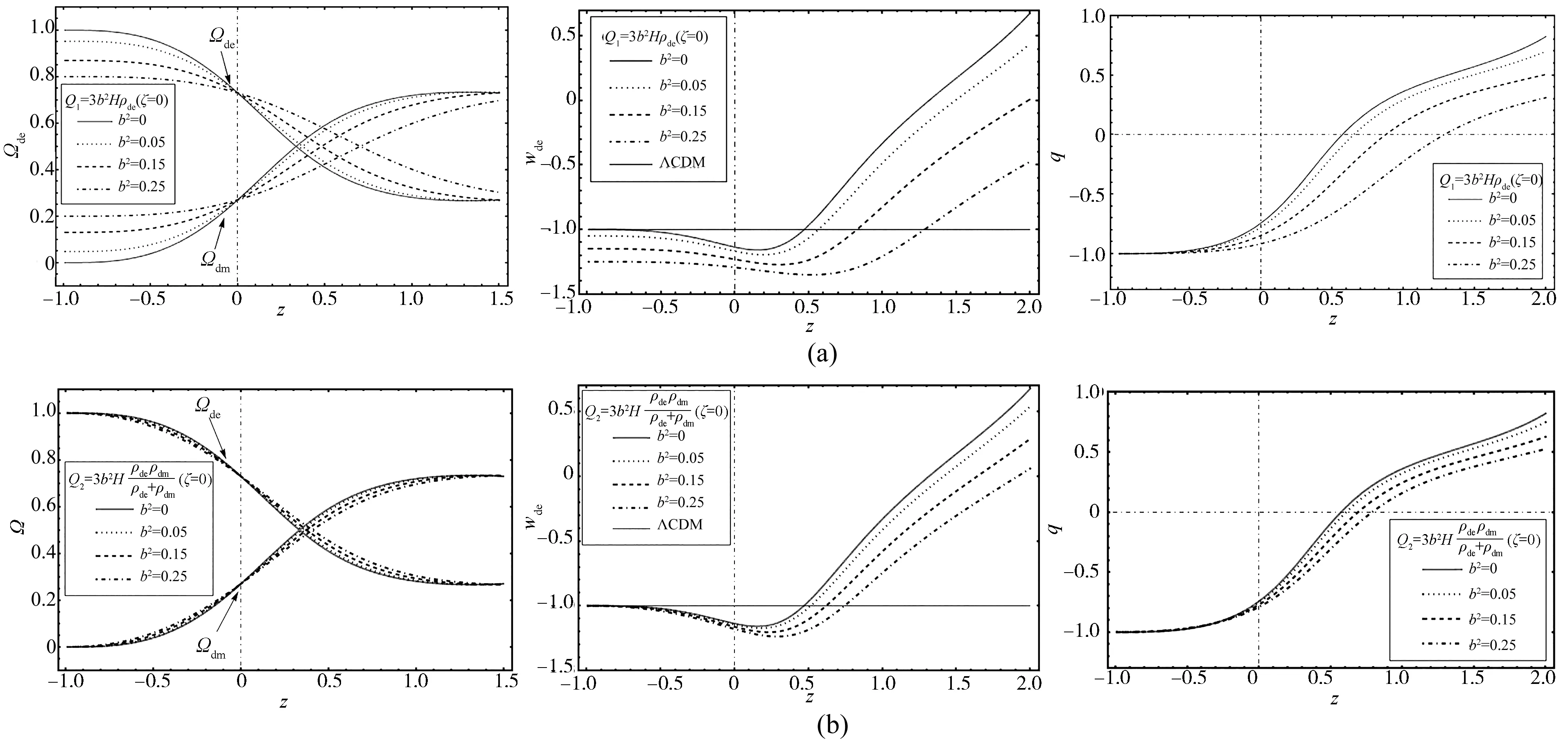
图1 当无黏滞性时，耦合参数b2对Ω、wde以及q演化轨迹的影响

2 具有黏滞性的Sharma-Mittal全息暗能量模型

Khalatnikov和Befinsky最早将黏滞性与宇宙学相结合，并由此提出了具有黏滞性的宇宙学[31].当考虑黏滞性时，宇宙的有效压强将变为

(21)

其中,pde表示无黏滞性时的压强，ζ表示体黏滞系数.不难发现当ζ=0时就可退回到无黏滞性的情况.

2.1 仅暗能量具有黏滞性的SMHDE模型的宇宙学演化

当仅考虑暗能量具有黏滞性时，选取

(22)

其中,ν称为黏滞系数.于是方程(9)变为

(23)

可得到

(24)

(25)

(26)

其中，“′”代表对lna的导数，Ξ依旧定义为Ξ=Gπc2H2(πδ/H2+1)R/δ-(2Ωde-1)(πδ+H2).容易发现仅当暗能量具有黏滞性时，体黏滞系数ζ并不会影响减速参数和密度参数的演化，而只会影响态参数的演化.所以本节不再赘述减速参数和密度参数的演化特点，而只专注于态参数的演化.具体地

(1)当i=1，即相互作用项为Q1=3b2Hρde时

(27)

(2)当i=2，即相互作用项为Q2=3b2Hρdeρdm/(ρde+ρdm)时

(28)

图2描述仅考虑暗能量具有黏滞性，且相互作用项取为Q1=3b2Hρde及Q2=3b2Hρdeρdm/(ρde+ρdm)时，黏滞系数ν对SMHDE模型态参数演化轨迹的影响.由图可以看到，只有当黏滞系数ν=0和ν=0.06时，SMHDE模型的态参数在两种不同相互作用形式下才均可实现Phantom界限的穿越，且黏滞系数ν的数值越大，越晚实现穿越.而黏滞系数值为ν=0.12时，只有Q1下的wde才能穿越-1，但当取黏滞系数为ν=0.18时，两种不同相互作用形式下的wde均无法穿越Phantom界限.当耦合参数b2=0.15、黏滞系数ν=0且相互作用项为Q1=3b2Hρde时的wde最早穿越Phantom界限，此时的穿越红移为zc=0.83；当耦合参数b2=0.15、黏滞系数ν=0.12且相互作用项为Q1=3b2Hρde时的wde最晚穿越-1，此时的穿越红移为zc=0.31.

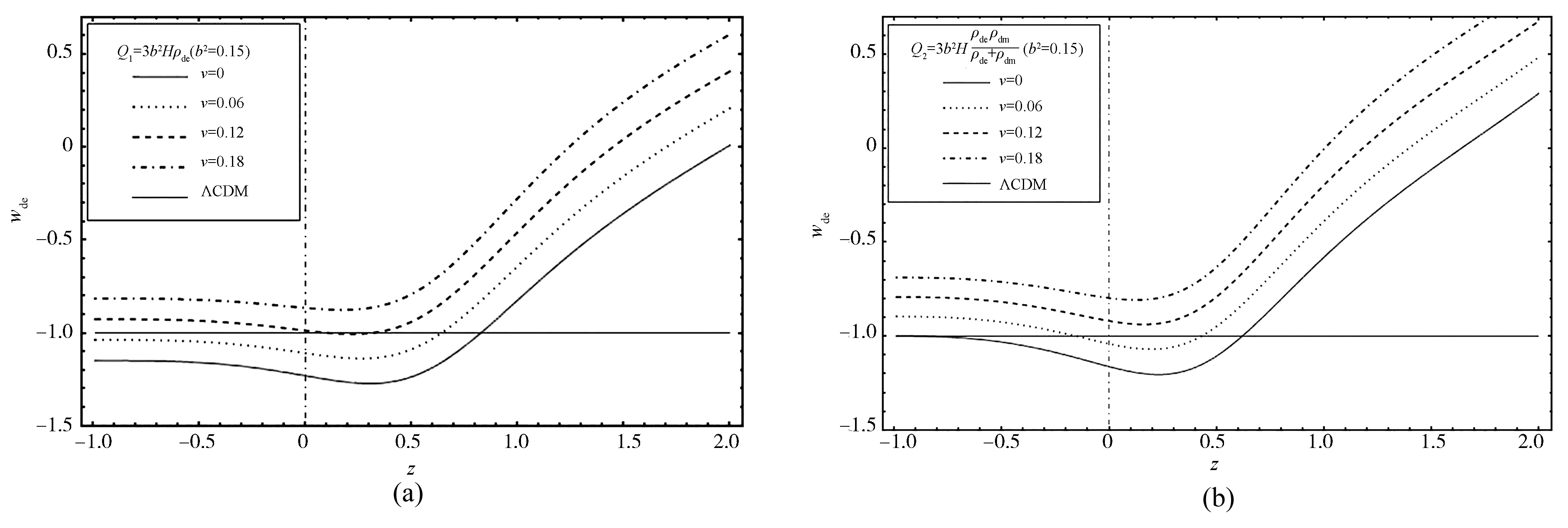
图2 仅考虑暗能量具有黏滞性，且固定耦合参数b2=0.15时，黏滞系数ν对wde演化轨迹的影响

2.2 仅暗物质具有黏滞性的SMHDE模型的宇宙学演化

当仅考虑暗物质具有黏滞性时，其Friedmann方程并不会改变，但其连续性方程变为

(29)

(30)

此时密度参数、态参数和减速参数可分别表示为

(31)

(32)

(33)

不难看出，仅暗物质具有黏滞性时，相互作用项Qi以及体黏滞系数ζ则会影响到相互作用的SMHDE模型的宇宙学演化.根据Hernandez-Almada等人的研究[32]，此时假设

(34)

为与上述区别起见，这里用μ代表此情况下的黏滞系数.

(1)当i=1，即相互作用项为Q1=3b2Hρde时

(35)

(36)

(37)

(2)当i=2，即相互作用项为Q2=3b2Hρdeρdm/(ρde+ρdm)时

(38)

(39)

(40)

图3为仅考虑暗物质具有黏滞性,且相互作用项取为Q1=3b2Hρde和Q2=3b2Hρdeρdm/(ρde+ρdm)时，SMHDE模型中黏滞系数μ对各宇宙学量演化轨迹的影响.两种不同相互作用形式下的SMHDE模型密度参数演化图像均显示出：在高红移区域，暗能量密度参数随着黏滞系数μ的增大而减小；在低红移区域，暗能量密度参数却随着黏滞系数μ的增大而增大.从过去(z>0)到未来(z<0)，暗能量密度参数在逐渐变大，这说明宇宙正逐渐演变为由暗能量主导.从两种不同相互作用形式下SMHDE模型的态参数wde图像中可以看到，不同黏滞系数μ的值对这两种相互作用形式下的态参数wde都表现为在过去影响较大、在未来影响较小的特点，且它们都可以穿越Phantom界限.从态参数演化图像可以得出，宇宙在未来不会发生大劈裂.从图中也可以看出，黏滞系数μ对Q2条件下减速参数q的影响，要明显比Q1的小.但两种情况下的减速参数q都随着红移z单调递增，这显示出宇宙是从减速膨胀转变为加速膨胀，且由图可知，黏滞系数μ越大便越早实现这种转变.

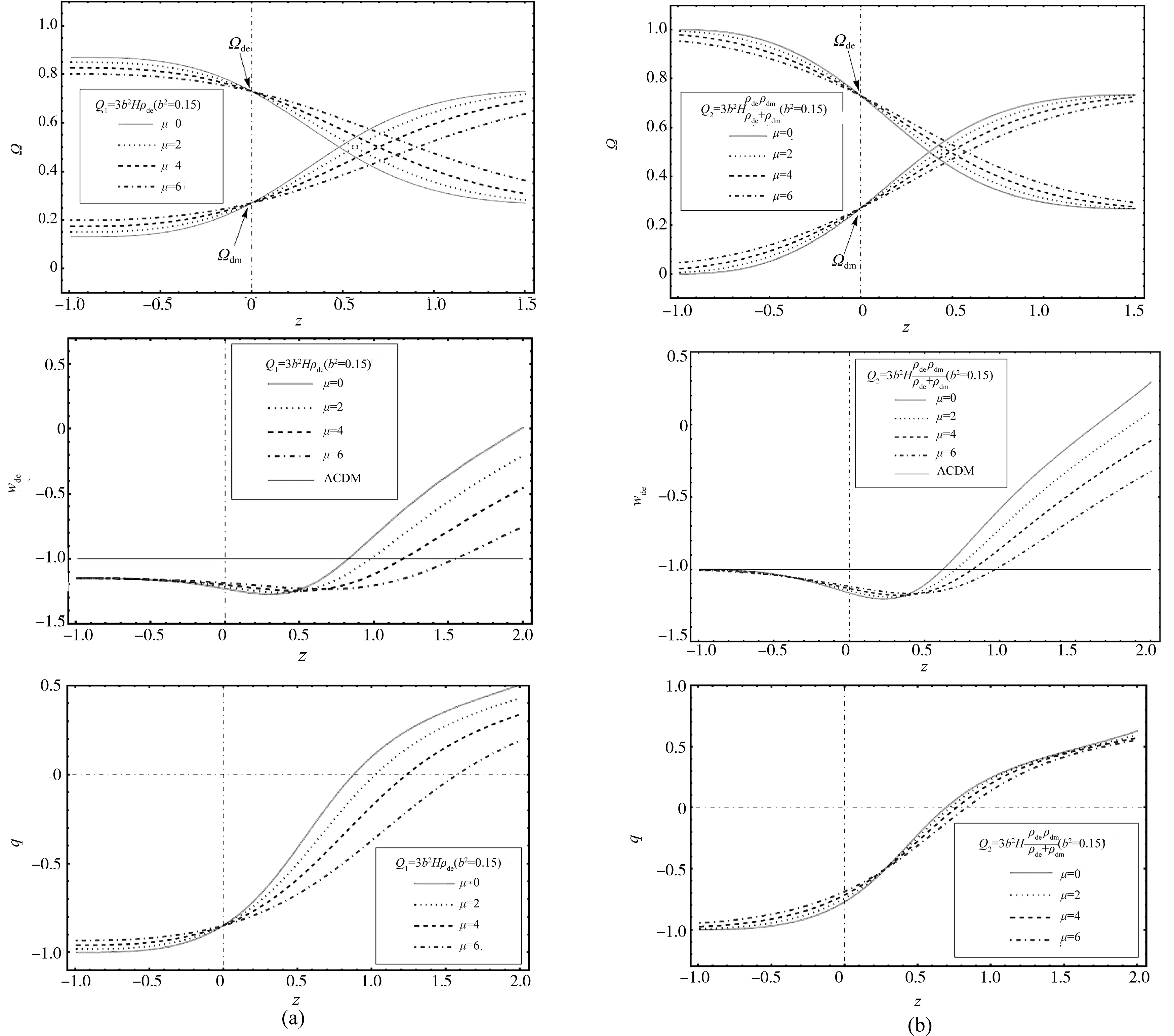
图3 仅考虑暗物质有黏滞性，且b2=0.15时，黏滞系数μ对Ω、wde以及q演化规律的影响

表1还列出了无黏滞性和仅考虑暗物质具有黏滞性时，相互作用SMHDE模型在Q1和Q2条件下的转换红移zT.因仅考虑暗能量具有黏滞性时，黏滞系数并不影响减速参数q的演化，所以表格中无此情况下的转换红移.由表中数据不难得到，当不考虑黏滞性且暗能量和暗物质之间无相互作用(b2=0)时，宇宙最晚实现从减速膨胀到加速膨胀的转变，此时的转换红移为zT=0.57.当仅考虑暗物质具有黏滞性且参数b2=0.15、μ=6时，Q1条件下的SMHDE模型最早转变为加速膨胀状态，此时的转换红移为zT=1.57.

表1 当无黏滞性和仅考虑暗物质具有黏滞性(取b2=0.15)时，相互作用SMHDE模型的不同转换红移

3 几何诊断

3.1 Statefinder几何诊断

为了区分不同的暗能量模型，Sahni曾提出一种模型独立的几何诊断方法，称为Statefinder诊断[33].在平直的FRW宇宙下，Statefinder几何诊断的参数定义如下

(41)

(42)

(43)

(44)

于是，能导出不同情况下参数r和s的表达式如下：

不考虑黏滞性：

(1)当i=1，即相互作用项为Q1=3b2Hρde时

(45)

(46)

(2)当i=2，即相互作用项为Q2=3b2Hρdeρdm/(ρde+ρdm)时

(47)

(48)

仅考虑暗能量具有黏滞性:

(1)当i=1，即相互作用项为Q1=3b2Hρde时

(49)

(50)

(2)当i=2，即相互作用项为Q2=3b2Hρdeρdm/(ρde+ρdm)时

(51)

(52)

仅考虑暗物质具有黏滞性:

(1)当i=1，即相互作用项为Q1=3b2Hρde时

(53)

(54)

(2)当i=2，即相互作用项为Q2=3b2Hρdeρdm/(ρde+ρdm)时

(55)

(56)

在图4中，分别画出了在两种不同相互作用形式下，不考虑黏滞性、仅暗能量具有黏滞性和仅暗物质具有黏滞性时，Statefinder几何诊断参数r和s的演化图像.图中红点表示它们的今天值，红色箭头代表演化的方向，黑色星星表示的是ΛCDM模型的固定点(r=1，s=0).具体地，当无黏滞性时，探究了耦合参数b2的值对Statefinder几何诊断的影响；当考虑黏滞性时，固定耦合参数b2=0.15，分别画出了相对应的黏滞系数对Statefinder几何诊断的影响.从图像中我们可以看到，取不同黏滞系数值时Statefinder几何诊断的演化曲线有明显差异，这表明该模型对黏滞系数很敏感，并且所有的Statefinder几何诊断演化轨迹都经过了ΛCDM模型固定点(r=1，s=0).可见，Statefinder几何诊断能很好地将SMHDE模型与ΛCDM模型区分开来.

3.2 Om几何诊断

除了Statefinder几何诊断之外，还存在一种不依赖物质的密度而只依赖膨胀率的几何诊断方法——Om诊断[34].Om诊断的定义为

(57)

其中，h(x)=H(x)/H0，x=1+z.H(x)是哈勃参数，H0表示哈勃参数的今天值.对于ΛCDM模型来说，Om(x)=Ωdm0，它是一个不随时间变化的常数，故可以利用这种方法把不同的暗能量模型区分开来.

图5中，分别画出了在两种不同相互作用形式下，无黏滞性、仅暗能量具有黏滞性和仅暗物质具有黏滞性时，Om几何诊断的演化图像.在无黏滞性时，描绘出耦合参数b2对Om几何诊断演化轨迹的影响；当考虑黏滞性时，固定耦合参数b2=0.15，分别画出了不同黏滞系数的值对Om几何诊断演化图像的影响.由图可以明显看到，当无黏滞性时，两种不同相互作用形式下的Om值都随耦合参数b2的增大而减小.而仅考虑暗能量具有黏滞性时，两种不同相互作用形式下的Om值都随耦合参数b2的增大而增大.当仅考虑暗物质具有黏滞性时，黏滞系数对Om几何诊断演化图像的影响，要明显比不考虑黏滞性以及仅考虑暗能量具有黏滞性的小.

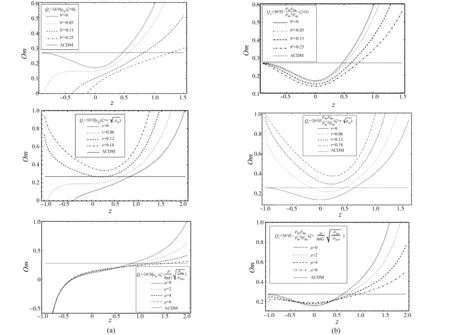
图5 在无黏滞性、仅暗能量具有黏滞性和仅暗物质具有黏滞性3种情况下Om几何诊断的演化轨迹

4 结 论

本文深入研究了具有黏滞性的相互作用Sharma-Mittal全息暗能量(SMHDE)模型的相关问题.具体地，空间均匀且各向同性的平直宇宙仅由Sharma-Mittal全息暗能量和暗物质构成，且它们之间存在相互作用.本文选取它们之间的相互作用项为Q1=3b2Hρde和Q2=3b2Hρdeρdm/(ρde+ρdm).在此基础上，首先讨论了无黏滞性、仅暗能量具有黏滞性和仅暗物质具有黏滞性三种情况下，各宇宙学量的演化.研究发现，当无黏滞性时，耦合参数b2对各宇宙学量演化的影响在Q2条件下比Q1的小，其具体表现为在未来(z<0)Q2条件下的各宇宙学量均对耦合参数不敏感.当仅考虑暗能量具有黏滞性时，通过固定耦合参数b2=0.15，发现黏滞系数ν并不会影响密度参数和减速参数，而只会影响态参数wde的演化，且wde的值随着黏滞系数ν的增大而增大.当仅考虑暗物质具有黏滞性时，同样固定耦合参数b2=0.15，然而此时的黏滞系数μ对密度参数、减速参数和态参数的演化都会产生影响.进一步，对具有黏滞性的相互作用SMHDE模型进行了Statefinder几何诊断和Om几何诊断.从它们各自的演化图像可以看到，这两种诊断方法不仅能很好地将SMHDE模型与ΛCDM模型区分开，而且可以明显看到耦合参数和黏滞系数对此模型的影响.