一种基于隶属度函数在线学习优化策略的 T-S模糊系统的L2-L∞/H∞混合控制
董久祥, 张振兴
(东北大学 信息科学与工程学院,辽宁 沈阳 110819)
现如今,大多数系统已演变成复杂的非线性系统,给系统的控制带来了极大的困难.20世纪80年代,两个著名的日本学者 Takagi和 Sugeno根据模糊控制理论提出了 Takagi-Sugeno (T-S)模糊模型来处理复杂的非线性系统[1],为非线性系统的控制与分析铺平了道路. T-S模糊模型对非线性系统具有很强的逼近能力.它利用如果-那么规则将复杂的非线性系统描述成一系列局部线性子系统的线性组合,通过隶属度函数将线性子系统联接起来,从而借用线性系统理论对模糊系统进行分析与控制[2-3].T-S模糊模型的应用特别广泛,例如:汽车悬架系统[4],三相并联电力滤波器[5],机器人[6],等等.通过利用 T-S模糊模型,非线性系统的模糊控制得到了很好的解决.
在模糊控制中,使用并行分布式补偿机制所设计的模糊控制器要和系统享有相同的前件变量,模糊集合以及隶属度函数,这在一定程度上限制了模糊控制器的设计灵活度.相比并行分布式补偿机制,非并行分布式补偿控制可以允许设计者对模糊控制器使用不同的前件变量,模糊集合和隶属度函数.因此,在一定程度上,后者可以极大地提高模糊控制器的设计灵活度[7].值得注意的是,在已有的控制文献中,基于非并行分布式补偿原则所设计的模糊控制器的隶属度函数都是任意选取的,只要保证在每一个隶属度函数的可行域范围之内即可.众所周知,不同的隶属度函数的选取将会导致整体的模糊控制增益的不同,进而会使得系统产生不同的性能响应,如收敛性,跟踪性能,抗故障性能, H∞性能,等等.因此,已有文献的控制方法仅仅能够维持系统稳定,而不能使系统达到一个最优的性能响应.另一方面,在实际工业应用中,通常需要受控输出的峰值要小于一定的界限, L2-L∞控制理论可以很好地解决这一问题[8].此外,传统的H∞控制也是衡量系统性能的一个重要指标,如何协同设计这两个重要的性能指标,并利用先进的智能算法针对这一个特定的混合性能指标来实时地优化隶属度函数进而得到该性能的最优响应,是一个非常具有研究意义的工作.为此,本文提出了一种新颖的隶属度函数在线学习优化算法实时地更新模糊控制器隶属度函数.相比传统控制方法,该算法不仅能够稳定系统,还能够最大程度地优化系统的性能.最后,给出了相应的仿真验证了本文所提出方法的有效性.
1 问题描述
本文考虑了一类带有r个模糊规则的非线性离散系统,其详细的建模规则如下:
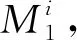
x(k+1)=Aix(k)+Biu(k)+Bwiw(k),z(k)=Ciy(k)+Diu(k),
y(k)=Cx(k).

(1)
y(k)=Cx(k).

考虑到系统的状态通常是不可测的,本文设计了与系统享用不同的前件变量,模糊集合以及隶属度函数的模糊静态输出反馈控制协议,详细的建模如下:
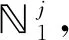
u(k)=Kjy(k).
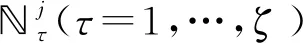
(2)
其中,wj(ψ(k))表示每一个子控制器的隶属度.
结合式(1)和式(2),可以得到如下的闭环系统表达式:
(3)
y(k)=Cx(k).
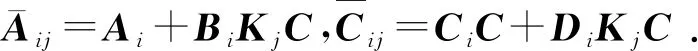
定义1[8]在0初始状态下,对于给定的γ> 0,如果被控输出z(k)满足
(4)
那么,闭环系统(3)满足L2-L∞/H∞混合性能指标.
注1式(4)是一个更为一般的性能表达式,因为选取不同的权重参数α,它可以被转成标准的H∞性能指标和L2-L∞性能指标.如果α=0,条件(4)就变成了H∞性能;如果α=1,条件(4)就退化成了L2-L∞性能;如果 0<α<1,条件(4)就是L2-L∞/H∞混合性能.
2 主要结果
本章节首先给出了设计模糊静态输出反馈控制器的充分条件.随后,一个新颖的隶属度函数在线学习算法被首次提出来实时地获取最优的隶属度函数的值,进而得到更好的混合性能指标.
定理1对于给定的参数 0≤α≤1,0<κi≤1(i=1,…,r)和γ>0,在保证wj-κjmj≥0的情况下,如果存在正定对称矩阵P,对称矩阵Ω和控制器Kj(j=1,…,r)使得如下的线性矩阵不等式成立:
(5)
(6)
(7)
(8)
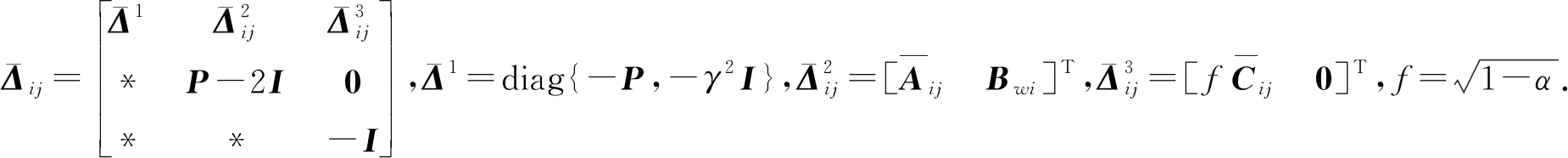
证针对闭环系统(3),选取李雅普诺夫函数V(k)=xT(k)Px(k).进而,可以得到
J=ΔV(k)+(1-α)zT(k)z(k)-γ2wT(k)w(k)≤
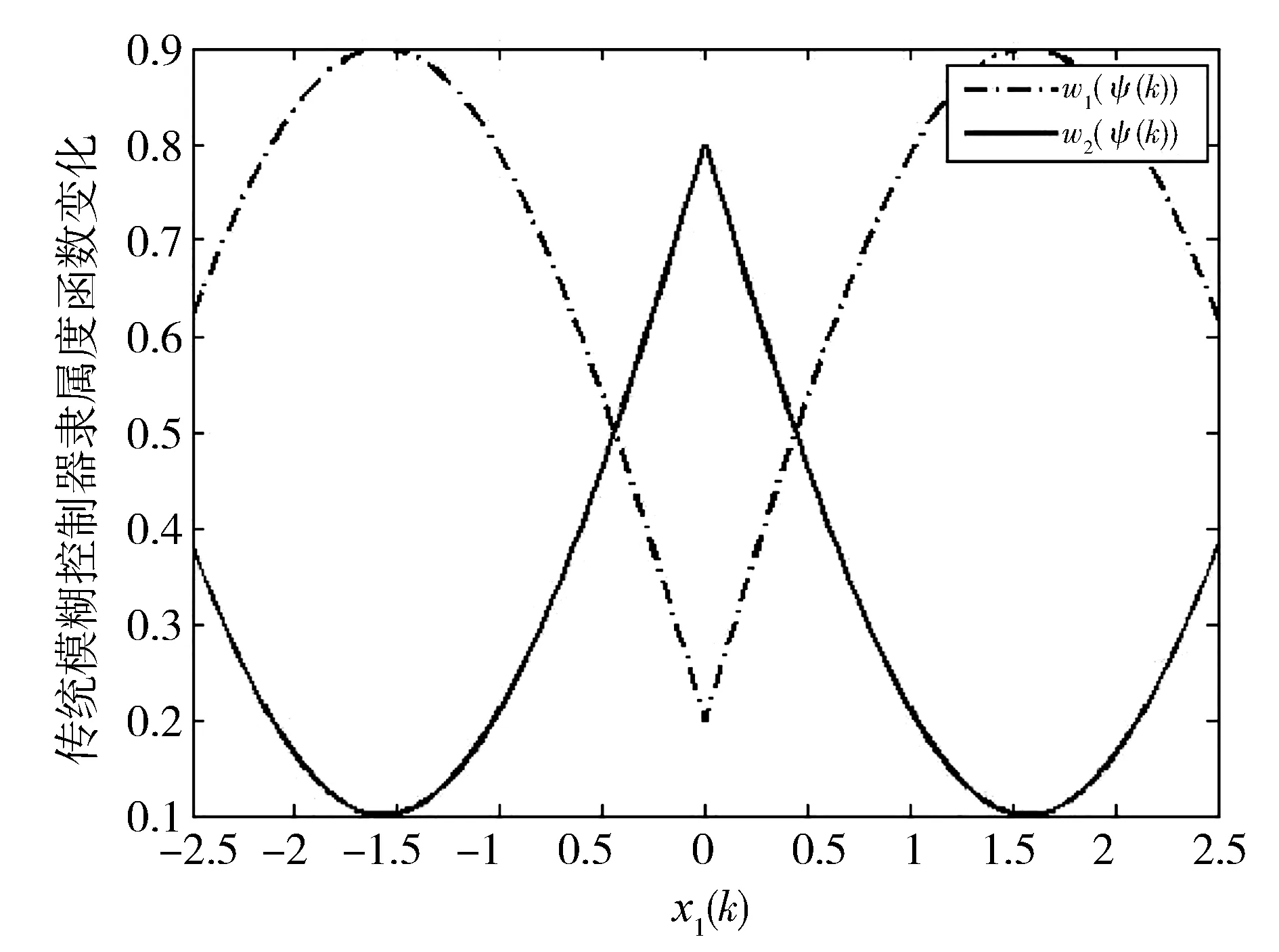
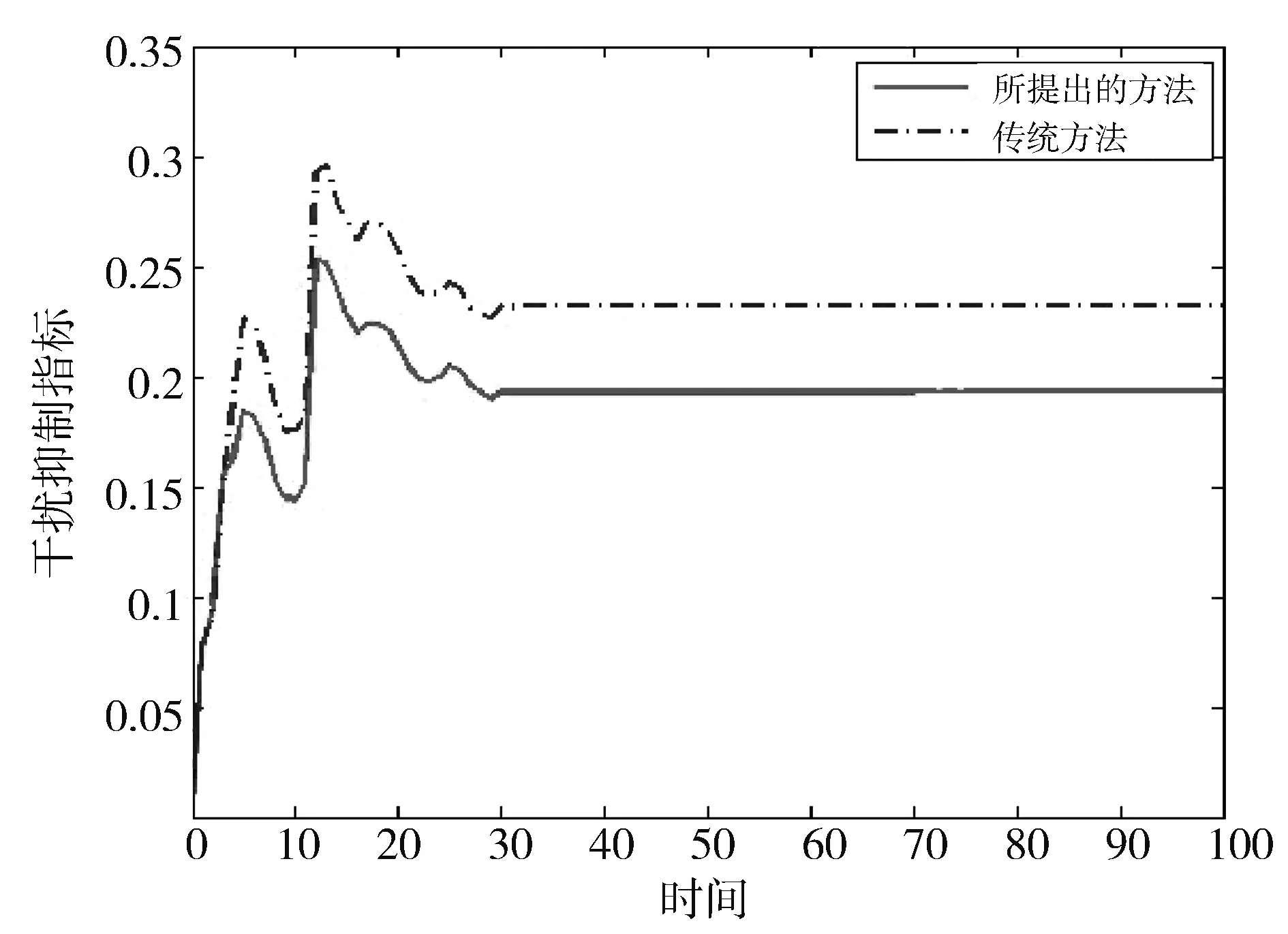
其中,φ(k)=[xT(k)wT(k)]T.因为-P-1 κiΔii-κiΩ+Ω<0, (9) κjΔij-κjΩ+κiΔji-κiΩ+2Ω<0,i (10) Δij-Ω<0. (11) 这也就意味着 J=ΔV(k)+(1-α)zT(k)z(k)-γ2wT(k)w(k)<0 是成立的.于是有 (12) αzT(k)z(k)-V(k)<0 (13) 通过式(12)和式(13),可以得到 因此,闭环系统(3)满足混合性能指标(4).此外,当外部干扰为0时,通过所给出的定理可以很容易得到闭环系统是渐近稳定的.证毕. 通过定理1不难发现在非并行分布式补偿机制下,模糊控制器的隶属度函数在可允许变化范围内是可以自由选取的.也就是, κjmj≤wj≤1(j=1,…,r). (14) 然而,在已有的非并行分布式补偿控制文献中,模糊控制器的隶属度函数往往都是任意选取的,只要保证在上述可行域(14)里面就可以.但是这种选取方式仅仅能够维持系统的稳定性,并不能使得系统达到最优的性能响应.不同的控制器隶属度函数的选取会使得系统产生不同的系统性能响应,比如:收敛速度,抗干扰能力等等.因此,针对一个特定的系统性能,如何设计一个智能算法去优化控制器隶属度函数进而获取最优的性能响应是很有意义的.受上述讨论的启发,本文提出了一种隶属度函数在线学习算法来寻求最优的控制器隶属函数进而实现最优的混合性能响应. 为了在控制器隶属度函数可行域(14)内实时优化其值进而获取最优的混合性能响应,本文首次提出了一个利用梯度下降法的隶属度函数在线学习策略.根据混合性能指标表达式,不难发现,对于每一个模糊规则,如果通过实时地调节控制器隶属度函数使得‖z(k)‖2尽可能的小,那么,干扰抑制性能指标γ就可以被降低.为此,定义成本函数E(N)如下: (15) 每一个隶属度函数wj的梯度可以表示为如下形式: 每一个隶属函数的迭代如下: wj(N+1)=wj(N)+Δwj(N). (16) 值得注意的是,为了便于比较,在进行如上迭代的过程中,模糊控制器隶属度函数的初始迭代值要和传统控制方法的初始值保持一致.此外,如果控制器隶属度函数的迭代值超过了可行域,则继续沿用上一时刻的迭代值.所以,经由式(16)迭代出来的隶属度函数的值总是能保持在可行域内. 注2式(16)的迭代需要一个大小合适的学习率βf,因为如果βf太小将会导致迭代速度缓慢;相反地,βf太大将会导致成本函数不收敛.因此,下一节给出了如何选取合理的学习率βf. 定理2如果学习率参数βf满足 (17) 其中, 其中,参数ξ是一个极小的正数.那么,成本函数(15)的收敛性将会得到保证. 证对于成本函数(15),考虑如下的李雅普诺夫函数: 其差分计算如下: (18) 进而有 (19) 和 (20) 根据所得结果式(19)和式(20),有 (21) 将式(21)带入式(18),有如下结果: (22) 本节给出了一个数值例子来验证所提方法的有效性. 例1考虑带有两个模糊规则的非线性系统,其相关的参数如下: w1(ψ(k))=0.2+0.7|sin(x1(k))|和w2(ψ(k))=1-w1(ψ(k)), 不难看出它们严格满足隶属度函数限制(14).利用MATLAB计算定理1 中的线性矩阵不等式,相应的模糊控制器增益为:K1=[0.3717 -0.4707],K2=[0.380 6 -0.474 5]. 仿真结果如图1~图6所示.图1给出了系统隶属度函数的变化;图2描绘了在传统方法下所定义的控制器隶属度函数的变化;图3展示了利用所提出的隶属度函数在线学习算法优化后的隶属度函数的迭代轨迹;系统的状态响应如图4 所示;图5分别给出了在传统方法下以及在所提出的隶属度函数在线学习策略下的被控输出的二范数轨迹,显然,在本文所提出的算法下,被控输出的范数要比在传统控制方法下要小;图6分别刻画了在传统控制方法下和本文所提出的在线学习优化策略下性能指标γ曲线.显而易见,在本文所提出的控制方法下,γ要明显小于传统控制下的值.综上所述,本文所提出的控制算法要优于传统的控制方法. 图1 系统隶属度函数 图2 控制器隶属度函数 图3 基于在线学习算法的控制器隶属度函数轨迹 图4 系统状态轨迹 图5 ‖z(k)‖2 的轨迹 图曲线 本文研究了在非并行分布式补偿机制下,利用所提出的隶属度函数在线优化策略来实时地优化控制器隶属度控制参数,进而使系统取得最优混合性能指标的问题.首先,给出了保证系统稳定且满足混合性能指标的充分的静态控制器设计条件.紧接着,利用本文所提出的隶属度函数在线学习策略,模糊控制器的隶属度可以被实时地更新,再使用所更新的隶属度函数构造整体的模糊控制器,进而获取了最优的混合性能指标.最后,给出了一个数值算例验证了所提方法的有效性.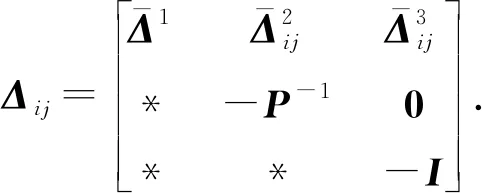
3 隶属度函数在线学习

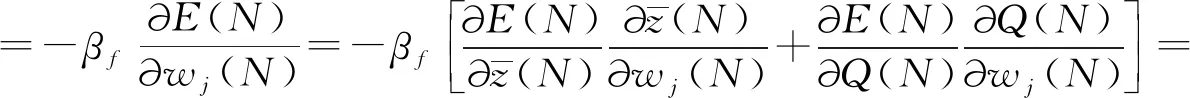
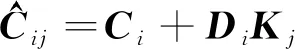
4 收敛性分析

5 仿真算例




6 结 论

