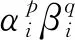带边Seifert流形的H′-分解的结构
雷逢春, 徐 妍
(大连理工大学 数学科学学院,辽宁 大连 116024)
每个紧致连通可定向三维流形M都有Heegaard分解, 即存在M中一个可定向闭曲面F,F把M切成两个压缩体C1和C2,C1∩C2=∂+C1=∂+C2=F,C1∪FC2=M.最近, 可以证明, 任意紧致连通可定向三维流形M都有H′-分解,即存在M中一个紧致连通可定向曲面F,F把M切成两个柄体H1和H2,H1∩H2=F,H1∪FH2=M.显见,当M是闭三维流形时,Heegaard分解与H′-分解是一致的;当M是带边三维流形时,Heegaard分解与H′-分解是不同的分解,文[1]给出了柄体的H′-分解的特征描述.
Seifert流形是一类重要的三维流形, 其拓扑分类已完全清楚, 对其Heegaard分解的结构也有着很透彻的了解.如在文[2]中,J. Schultens给出了带边Seifert 流形的特征描述, 在文[3]中, J. Schultens给出了紧致可定向曲面×S1的Heegaard分解的分类,在文[4]中,Y.Moriah和J.Schultens证明了Seifert流形的不可约的Heegaard分解或是竖直的,或是水平的.
本文研究了带边Seifert流形的H′-分解的结构,主要结果给出这类流形的H′-分解的特征描述.本文第2节介绍了必要的预备知识和若干引理,第3节给出主要定理和证明.
1 预备知识
本文中涉及的三维流形和曲面都默认是紧致可定向的,未详细定义的概念都是标准的,可参见文[5]或文[6].
设D为平面上的单位圆盘,D上的点用极坐标(θ,r)表示.设p和q为一对互素的整数,p>0.显然,商空间D×I/(θ,r,0)~(θ+2πq/p,r,1)为一个实心环(≌D×S1),记作T(p,q).记商映射为ρ:D×I→T(p,q).对于圆心O∈D,e=ρ({O}×I)是T(p,q)中的一条简单闭曲线;对于x=(θ,r)∈D{O},ρ((θ,r,0)×I)∪ρ((θ+2πq/p,r,0)×I)∪…∪ρ((θ+2πq(p-1)/p,r,0)×I)是T(p,q)中的由p条简单弧依次首尾相连构成一条简单闭曲线.这些简单闭曲线均称为是T(p,q)的纤维.称T(p,q)为一个标准的(p,q)-型纤维化实心环.若p>1,称e为T(p,q)的奇异纤维,称T(p,q)的非e纤维为正则纤维.当p=1时,T(1,q)的每个纤维均为正则纤维.
容易看到,T(p,q)是它的所有纤维的无交并.
设T1、T2是两个标准的纤维化实心环(型可能不同),h:T1→T2为一个同胚.若h把T1的每个纤维送到T2的纤维,则称h为保纤同胚.此时,也称T1和T2是同构的.
定义1设M是一个3-流形.若M可以分解成一族互不相交的简单闭曲线(称每个这样的简单闭曲线为一个纤维)的无交并,使得每个纤维在M中有一个管状邻域保纤同胚于一个标准的纤维化实心环,则称M为一个Seifert流形.
将Seifert流形M的每个纤维粘成一点所得的商空间是一个曲面B,称之为M的底空间,对应的商映射记为π:M→B.M的每个奇异纤维在底空间B上的像点称为奇点.显然,每个奇点都是B的孤立点,即它在B上有一个邻域,其中,只有其本身是奇点.若M是紧致的,则M只有有限多个奇异纤维,这时B只有有限多个奇点,且落在B的内部.
令S为M所有奇异纤维之并,s=π(S)为所有奇点之集,则π|MS:MS→Bs是曲面Bs上的一个S1-丛.由此可知,紧致可定向的Seifert流形M的每个边界分支均为环面.详可参见文[7].
定义2设M为一个紧致Seifert流形,F为M中一个真嵌入曲面.若F为M中若干正则纤维之并,则称F是一个竖直曲面;若F与M的所有纤维均横截相交,则称F是一个水平曲面.
定义3设M1,M2为两个紧致连通可定向三维流形,Fi⊂∂Mi是一个紧致连通曲面,i=1,2,h:F1→F2为一个同胚.令
M=M1∪M2/x~h(x),∀x∈F1,
称M为M1和M2沿F1和F2的一个融合,记作M1∪hM2,或M1∪FM2,其中,F=F1=F2.当M1和M2都是压缩体,且∂+M1=F=∂+M2,称M1∪FM2为M的一个Heegaard分解;当M1和M2都是柄体,称M1∪FM2为M的一个H′-分解.
定义4设N为m-流形M中一个嵌入的n-流形,n 从纤维丛理论可知,若紧致连通可定向3-流形M是闭曲面F上的I-丛,ρ为其伴随映射,则∂M是F上的∂I-丛,ρ|∂M:∂M→F是一个2重覆盖映射.M由ρ|∂M完全决定.若|∂M|=2,则M≌F×I;若|∂M|=1,则称M为一个扭的I-丛,此时,F是不可定向的曲面. 例 (1)设F为一个曲面,F×I、F×S1都是纤维丛,也称这样的纤维丛为积丛或平凡丛. (2)设M为一个莫比乌斯带,C为M上的中位线,则M是C上的I-丛.M为非平凡丛,通常称这样的丛为扭的I-丛.一般地,从Pn中除去一个开的n-球体所得的流形是Pn-1上扭的I-丛. 三维流形中的不可压缩曲面的定义、边界不可压缩的曲面的定义可参见文[5]或文[6].若三维流形M中的一个真嵌入曲面F是不可压缩的、边界不可压缩的,且F不平行于∂M的子曲面,则称F是M中的一个本质曲面.特别地,若F是一个2-球面,且F不界定M中一个实心球,则称F为一个本质球面.若M包含一个本质球面,则称M是可约的,否则,称M是不可约的. 引理1设M=M1∪FM2是两不可约三维流形M1和M2沿F的融合.若F在M1和M2中均是不可压缩的,则M是不可约的. 引理1的证明可参考文[8].下面引理出自文[7],将在第3节中用到. 引理2设M为一个紧致连通不可约可定向的Seifert流形.则M中的每个本质曲面可以同痕于一个水平曲面或一个竖直曲面. 下面给出紧致连通可定向带边Seifert流形的H′-分解的特征描述. 定理1设M为一个紧致连通可定向带边流形,H1∪FH2是M的一个H′-分解.假设F在H1和H2中均是不可压缩的.则M是一个Seifert流形当且仅当M为下列两种情形之一: (1)H1和H2均为实心环体,且曲面F是∂Hi上的竖直平环,i=1,2;或 (2)对于i=1,2,Hi是Si上的扭I-丛,ρi为其伴随映射,ρi|F:F→Si是一个2重覆盖映射,且粘合映射h:F→F是周期自同胚. 证首先证明必要性.由假设和引理1可知,F在M中是不可压缩的,M是不可约的.M是一个紧致带边可定向Seifert流形,故∂M的每个分支都是环面.由引理2,F同痕于M中一个水平曲面或竖直曲面.下面就这两种情形分别讨论. 情形1:F同痕于一个竖直曲面. 不妨设F就是一个竖直曲面.F为M的若干正则纤维的无交并,故F是一个S1-丛,从而F或是一个平环,或是一个环面,或是一个Klein瓶.因F是带边曲面,F只能是一个平环.又∂M的每个分支都是环面,故∂F所在的∂Hi的分支均为环面,i=1,2.因Hi是个柄体,从而Hi是一个实心环体,且F是∂Hi上的竖直平环,i=1,2. 情形2:F同痕于一个水平曲面. 不妨设F就是一个水平曲面.设π:M→B为M到底空间B的商映射.此时F到底空间B的投射πF:F→B是一个n-重的分歧覆盖,使得对M的每个(p,q)-型纤维化实心环中的奇异纤维C,π(C)是个重数为p的分歧点,p整除n. 因πF:F→B是满射,F与M所有纤维都相交.M的纤维均与F横截相交,从每个纤维的标准化邻域与F相交的每个分支的局部情况可知沿F切开M所得流形MF是一个I-丛. F分离M为柄体H1和H2.对于i=1,2,每个Hi是其中的嵌入曲面Si上非平凡的I-丛,否则,Hi=Si×I,F=Si×{0},Si×{1}⊂∂M,矛盾.这样,每个Hi是Si上的扭I-丛,ρi为其伴随映射,ρi|F:F→Si是一个2重覆盖映射,i=1,2.由πF:F→B是一个n-重的分歧覆盖可知,粘合映射h:F→F是周期为n的自同胚. 充分性显然.定理得证.2 主要定理及证明