学生学情的初中数学教学案例分析

胡引红

一、案例背景

本节课要讲的内容人教版九年级上册中的“圆”中。圆是一个常见的几何图形，它就像正方形与长方形一样，有着很多性质。但是却有着比前两者更多的性质值得去探究。在日常生活中，圆也随处可见，比如车轮等。古希腊数学家毕达哥拉斯认为“一切平面图形中最美的是圆”，因为它不论从哪个角度看，都是对称的。所以通过本节课的学习，希望学生对圆中的圆周角有更深的认识。

二、案例描述

（一）教学目标

1. 理解圆周角的概念，掌握圆周角的特性，并且与之前所学的圆心角比较异同

2. 可以灵活的运用简单的圆周角定理解决问题

3. 学会对圆周角定理的证明，同时可以培养学生的分析和想象的能力

4. 探索从特殊到一般，从一般到特殊的思想方法。

（二）教学重难点

重点：圆周角的概念和定理

难点：发现并能证明圆周角定理

（三）教学方法

教师、小组合作、多媒体演示

（四）教学课程设计分析

1. 通过ppt展示圆形的建筑，比如大厅里的支撑的圆柱体。横切面就是一个圆。把圆单独拿出来，选一个学生在圆上任意找三个ABC点，如图所示：

2. 认识圆周角

（1）通过提问，问题：∠ACB与∠AOB有什么异同吗？那么∠ACB又叫什么名字呢？

答案：∠ACB的其中顶点在圆上，而∠AOB的则在圆心，∠ACB叫做圆周角。

引出圆周角定义：顶点在圆周上，并且两边都和圆相交的角叫做圆周角。

（2）通过例题向学生展示几个图形，让学生运用圆周角定义辨别哪些是圆周角。

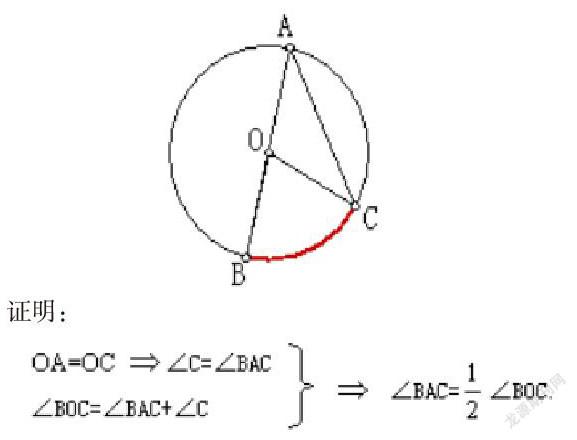
3. 圆周角定理证明

（1）教师提出问题：在圆O上，任意选取一个圆周角∠BAC，同弧相對的圆周角一共有几种情况呢？学生可以自己动手去画。

教师找人在黑板画出不同的情况，让学生针对进行总结。

归纳出：总共有三种情况：圆周角的一条边经过圆心;圆心角在圆周角的内部;圆心位于圆周角的外部。

（2）上面学生总结出来的三种情况，应该怎么去证明呢？

教师以第一种情况为例（圆周角的一边经过圆心），进行演示证明。

学生根据教师的例子进行思考和总结，并且自己证明第二和第三种情况

上面的证明对圆周角的定理进行了佐证，证明圆周角的定理是正确的。

4. 以上的证明，可以表现出数学中用到的那种方法呢？

答：体现出了数学中的化归思想，因为后两种情况都通过不同的辅助线或者其他的手段归为了第一种方法。

三、教学成果

（一）通过日常生活实例引入，引起学生的兴趣

教师通过多媒体展示了日常生活中的圆形物体。让学生有切身感受，发现生活中的例子，贴近生活，让学生可以快速接受，并且引起探究的兴趣。促使学生继续进行学习。

（二）引出ppt，展开新课教学

多媒体的运用，可以让学生更直观看到各种各样的圆形实物，并且色彩缤纷，课堂氛围会更活跃，画面式的记忆可以让学生更容易记住知识点。

（三）分小组合作，探究问题的答案

不论是在数学学习或者其他科目的学习中，小组合作完成是比较重要的事情。教师可以提出一系列问题，然后让学生以四个人或者多个人的方式进行讨论，用于发表自己的观点和看法，进行头脑风暴，这种方法不仅可以使得教学质量提高，还能培养学生的合作意识，明白团结协作的重要性。

（四）课后巩固练习，夯实基础

通过对课后练习题的布置，让学生进一步复习课堂所学知识，并能运用知识去解决问题，教师还应该在课堂末尾对知识进行拓展，提出思考题，让学生拓展思维。最终达到教学目的。

四、评价与反思

首先，本课程比较注重学习的探究活动的开展，比如小组讨论。但是也存在不足。

反思：每个学生的接受程度不同，没有根据不同的学生采取不同的方法;证明定理时，只给出了第一种情况的证明。后面两种情况有些学生可能不会证明，没有关心到每个学生。另外，教师只是直接给出证明步骤，没有引导学生自主去证明问题。应该及时引导和点拨学生。

评价：初中数学课程可能对于有些学生不是那么容易接受，这就要求教师根据不同的学生，不同的学情进行教授。对于那些接受的没有那么快的学生积极帮助，帮助他们更好的构建数学知识体系，让他们不觉得数学乏味。数学的学习还需要严密的逻辑能力与空间想象能力。除了学生在课堂上的学习之外，教师还要及时反馈学生课下的学习情况，教师只有做到课上和课下的结合，才能让学生牢固的掌握知识，并运用到生活中去。努力促进学生数学综合能力的提高，让学生爱上学数学，大胆提出自己对问题的看法。