Sc、Ce掺杂CrSi2的电子结构与光学性质的第一性原理

叶建峰，肖清泉，秦铭哲，谢 泉

(贵州大学大数据与信息工程学院，新型光电子材料与技术研究所,贵阳 550025)

0 引 言

硅化铬(CrSi2)是一种间接、窄带隙环境友好型半导体材料，具有优异的高温稳定性、抗氧化性、高效的热功率和高电导率[1-2]，同时，与其他过渡金属硅化物相比，CrSi2与硅衬底之间具有较小的晶格错配率，使得制备CrSi2/Si异质结成为可能。CrSi2的优良特性，使其在高温抗氧化涂层[3-4]、硅基光电器件[5]和热电转换[6]等多领域有着广泛的应用前景。

掺杂改性成为半导体材料研究的热点，引入杂质原子或杂质体系，能产生新的杂质能级和不同种类的载流子，推动体系能量分布的变动，从而达到调控材料特性的目的。近年来，众多学者分别通过掺杂过渡金属Ti[7-8]、Mn[9-10]、Cu[11]、V[12]、金属Al[13]、非金属B[14]和稀土La[15]等元素对CrSi2材料的光电、热电等性质进行研究。目前尚未有对Sc、Ce元素单掺、共掺CrSi2的研究，对于在元素周期表中分别与Sc、Ce邻近的Ti、La元素，闫万珺等[7]对Ti掺杂CrSi2的光电特性进行第一性原理研究表明，Ti置换Cr原子后掺杂体系晶格常数和体积增加，掺杂引入了杂质能级，Cr11TiSi24向p型半导体转变，带隙宽度由未掺杂前的0.38 eV变为0.082 eV，对光学性质的计算发现掺杂Ti的CrSi2介电峰发生了红移，吸收系数在低能区有所提升，掺杂后反射率和光电导率总体上有所降低。张忠政等[15]对La掺杂CrSi2的体系进行第一性原理研究表明本征CrSi2是间接带隙半导体，能带计算结果为0.38 eV，La掺杂后带隙变为0.07 eV，掺杂后CrSi2的静态介电常数虚部介电峰向低能方向偏移且增强,光学吸收边向低能方向移动,吸收峰减小。据以往研究，掺杂Sc元素能有效提高材料的热电性质、光学性质和电导率[16-18]，Ce元素的引入能调控材料的磁学性质和导电性质[19-21]。本文采用基于密度泛函理论的第一性原理赝势平面波方法对Sc、Ce单掺、共掺CrSi2的几何结构、能带结构、态密度和光学性质进行对比分析与研究。

1 理论模型及计算方法

1.1 理论模型

CrSi2晶胞为C40的六方晶体，空间点群为P6422，晶格常数为a=b=0.442 8 nm，c=0.636 9 nm，晶面角为α=β=90°，γ=120°[22]。

本文采用2×2×1的结构模型，在晶胞含有6个Si原子和3个Cr原子的基础上分别向a、b方向扩充一倍，得到CrSi2超胞模型如图1(a)所示。本文以本征CrSi2体系为基体，用一个Sc、Ce元素分别取代和两种元素共同取代一个Cr原子如图1(b)、(c)和(d)所示，得到本征和掺杂体系的模型如图1(a)～(d)所示。

图1 结构模型Fig.1 Structural models

1.2 计算方法

本文采用基于从头计算原理的密度泛函理论即DFT方法，首先利用CASTEP模块[23]对未掺杂及Sc、Ce掺杂的CrSi2模型进行结构优化，并对优化模型的电学和光学特性进行分析。CrSi2体系中的价电子波函数用平面波基矢展开，采用广义梯度近似(GGA)的PBE泛函来计算电子-电子之间的交换关联能[24]，离子实-电子的相互作用选用超软赝势来处理，布里渊区积分k的网络大小设置为4×4×5[25]，设置平面波截断能量Ecut为350 eV，计算中的收敛精度设置为5×10-7eV/atom，迭代步数上限为300，能量计算都在倒易空间中进行。

2 结果与讨论

2.1 几何结构

表1为本征和Sc、Ce掺杂CrSi2的晶格常数和晶胞体积的优化结果，本征几何优化所得结果与实验值相差不大[26]，表明利用广义梯度近似的PBE算法来处理电子之间的交换关联是相对可靠的。由于Sc、Ce的共价半径分别为1.64 nm和1.82 nm，Cr的共价半径为1.26 nm，掺杂元素半径较大，由量子化学理论可知，Sc、Ce替换Cr元素后，CrSi2体系的晶格常数、体积增加是合理的。

表1 未掺杂和Sc、Ce掺杂CrSi2的结构优化结果Table 1 Structural optimization results of undoped and Sc or Ce doped and co-doped CrSi2

2.2 电子结构

2.2.1 能带结构

为了便于比较分析掺杂对CrSi2体相能带结构的影响，首先计算了本征CrSi2晶体的能带结构如图2(a)所示，图中虚线代表费米能级且将其设置为能量零点。本征CrSi2的导带和价带主要由Cr的3d态电子和Si的3p态电子耦合杂化形成，其价带最高点位于A点,导带在G点取得最小值0.386 eV，由于将本征CrSi2的价带顶设置为能量零点，同时注意到导带最低点与价带最高点在k空间中并不处于同一位置，因此可知本征CrSi2的禁带宽度为0.386 eV，表现为间接半导体性质，结果与实验值相符[27]，与闫万珺[7]、张忠政等[15]计算本征CrSi2带隙为0.38 eV的结果相近，表明本文对2×2×1的CrSi2结构模型采用的计算方法是可靠的。图2(b)～(c)为Sc、Ce单掺CrSi2的能带结构，由图可知掺杂后的CrSi2能带结构变得复杂，导带和价带趋向平缓。过渡金属Sc掺杂后的CrSi2禁带宽度减小至0.245 eV，与闫万珺等[7]掺杂与Sc紧邻的Ti相比，Ti掺杂的CrSi2带隙从本征0.38 eV减小至0.082 eV。由于Sc-3d态电子的主要影响，在费米能级上方出现了一条杂质能级，杂质能级靠近导带底部，比禁带宽度小，位于杂质能带上的电子更易跃迁至导带中使得导带中的电子浓度增加，从而改善了CrSi2的导电性。

图2(c)为稀土元素Ce掺杂CrSi2的能带结构，价带最高点位于A点为0.236 eV，导带最低点位于G点为0.468 eV，带隙为0.232 eV，禁带内出现了两条位于价带上方靠近导带底部的杂质能级，较为靠近价带的一条杂质能级在K点处取得最小值且与价带顶有近零(0.029 eV)交叠，使得价带上的电子能更加顺利跃迁到杂质能带进而进入导带，进一步增强了CrSi2的导电能力。相较于Sc掺杂的CrSi2，Ce掺杂后的能带进一步朝高能方向移动，费米能级进入价带。图2(d)为Sc-Ce共掺CrSi2的能带结构，其价带最高点位于A点为0.217 eV，导带最低点位于G点为0.415 eV，带隙为0.198 eV。与单掺相比共掺后的CrSi2两条杂质能级在禁带中较为连续，电子最容易跃迁，光催化性能最强。

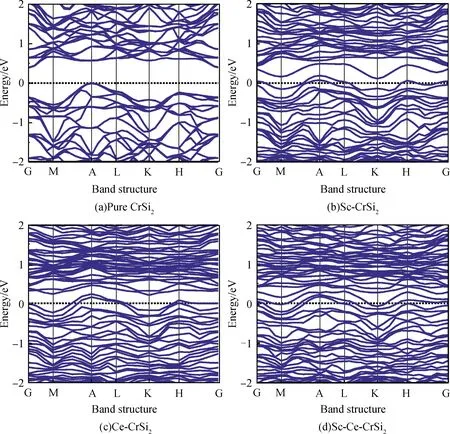
图2 能带结构Fig.2 Energy band structure

2.2.2 态密度

图3(a)～(d)为掺杂前后CrSi2的态密度分布曲线。本征CrSi2的态密度主要集中在能量较高的导带，同时导带分布的态密度曲线较价带而言相对平缓，Cr-3p、Si-3p态电子是导带和价带构成的主要贡献者，其中Cr-3p态电子集中在费米能级附近，Si-3p态电子主要分布在离费米能级较远的能区。

图3(b)～(d)为分别掺杂Sc、Ce以及Sc-Ce共掺后CrSi2的态密度图，由图可知掺杂体系的态密度分布与本征较为相似，掺杂元素Sc、Ce的态密度主要集中在导带，从而影响CrSi2体系在较高能区的态密度分布。Sc掺杂CrSi2的导带构成主要由Cr的3p和3d、Sc的3p和3d以及Si的3s和3p态电子贡献，价带的构成与本征CrSi2相似。掺杂元素Sc的引入影响了体系在导带的分布，其中Sc-3d态电子影响较大，Sc-3p态电子影响有限。注意到Sc元素的掺杂对本征CrSi2体系中Si的态密度分布有一定影响，本征态分布与其相比较为平缓。

Ce掺杂CrSi2体系的导带与本征态相比新增了杂质元素Ce的态电子，其中Ce-4f态电子对体系的态密度分布贡献最大，Ce的其他轨道态电子贡献有限。Ce元素的态密度主要分布在导带，价带几乎没有态密度分布，与掺杂前相比，Ce掺杂的CrSi2态密度整体朝高能区域移动。图3(d)为Sc-Ce共掺的CrSi2，Sc与Ce共掺后，对本征CrSi2体系的Cr元素的态密度分布产生了一定的影响，Cr-3d态电子在能量分布的位置几乎没有发生变化，但在费米能级附近的态密度曲线变得平滑。Sc-Ce共掺CrSi2的导带主要由Cr-3d、Sc-3d、Ce-4f和Si-3p态轨道电子构成，其他态轨道电子贡献有限，价带的构成与未掺杂的CrSi2相似。与本征CrSi2体系相比，Sc-Ce掺杂后的体系在费米能级附近电子态密度增加且变得较为连续。

图3 态密度曲线Fig.3 Curves of states density

2.3 光学性质

随着材料种类的不断丰富，人们对材料光学性质研究的关注度逐渐提高，通过诸如复介电函数、折射率、吸收率和光激发记忆光谱等方面的研究，可以理解材料的光学性质。从能带图可知，本征和Sc、Ce掺杂CrSi2的能带结构相似，由于材料的能带结构可以决定其光学性质，因此，掺杂后的CrSi2与本征的光学性质相似。本文主要通过材料的介电函数、吸收系数和光电导率三个方面来研究CrSi2体系的光学性质。

2.3.1 复介电函数

图4(a)、(b)为未掺杂与Sc、Ce掺杂CrSi2的复介电函数的实部图(a)和虚部图(b)。作为反映材料电子结构的重要参数，介电函数是能将材料的能谱与光学性质之间的关系充分体现的光学常数。在能量零点，未掺杂CrSi2的静态介电常数为37.26，随着光子能量的增加，在0.69 eV生成了一个较大的峰值37.63。Sc、Ce单掺和Sc-Ce共掺CrSi2的静态介电常数ε1分别为47.29、63.42、95.79，明显大于未掺杂CrSi2的ε1(37.26)，由于Sc、Ce掺杂的CrSi2在0到0. 69 eV内极化程度加强，因此掺杂体系限制电子的能力有所增加，进而导致Sc、Ce掺杂CrSi2的复介电函数实部较大。

图4 未掺杂与Sc、Ce掺杂CrSi2的介电函数与能量的关系Fig.4 Relationship between dielectric and energy function of undoped, Sc or Ce doped and co-doped CrSi2

图4(b)为介电函数虚部ε2图。未掺杂CrSi2的虚部在1.64 eV出现值为24.92的介电峰，与本征态相比，Ce单掺和Sc-Ce共掺的CrSi2在较低能区的第一峰值增大，分别为26.00、28.03，而Sc单掺的CrSi2减小，为24.79,同时Sc、Ce单掺和Sc-Ce共掺CrSi2的第一峰在低能区发生红移，移动的幅度依次增加，其中Sc掺杂CrSi2的移动幅度最小为0.13 eV，Sc-Ce共掺CrSi2的移动幅度最大为0.82 eV。在能量大于2.23 eV小于4.13 eV的范围，Sc、Ce掺杂CrSi2的介电函数虚部的值均比本征态高，说明在CrSi2中掺杂Sc、Ce元素后提高了相应能区的光跃迁强度，提升最大的来自Sc-Ce共掺的CrSi2。结合态密度图可知，未掺杂的CrSi2位于能量为1.64 eV的第一介电峰，对应了来自Si原子的s轨道电子与Cr原子的d轨道电子杂化后从价带到导带的间接跃迁，后续在4.73 eV处值为29.37 eV的介电峰值，来自价带间Si原子的p轨道电子到导带Cr原子的d轨道电子的带间跃迁。

掺杂Sc后的电子跃迁是由Cr-d态和Sc-d态混合态与Si-p态杂化后到导带的跃迁产生的,导致ε2(ω)的第一介电峰向低能方向移动，掺杂Sc后CrSi2与掺杂Ti[7]的1个虚部介电峰相比，Sc掺杂的ε2(ω)出现2个明显的介电峰，对应的能量分别为1.51 eV与4.64 eV。位于能量为1.51 eV的第一介电峰对应了来自Si原子的p轨道电子与Cr原子的d轨道电子杂化，同时受到Sc原子的d轨道电子影响，后续的介电峰来自价带间Sc原子的d轨道、Si原子的p轨道电子到导带Cr原子的d轨道电子的移动。掺杂Ce后的CrSi2在能量为1.42 eV时出现第一个介电峰，在4.68 eV处形成第二峰值为26.89，Sc-Ce共掺的CrSi2在0.82 eV、4.45 eV处有介电峰值为28.03、25.92。在0～1.64 eV范围，掺杂后的ε2(ω)的值均比未掺杂的大，结合能带结构和态密度图可知，这主要是由于Cr-3d 态电子、Si-3p 态电子、Sc-3d态电子和Ce-4f态电子跃迁。闫万珺等[7]、张忠政等[15]分别对CrSi2与Sc近邻的Ti、与Ce近邻的La进行掺杂，所求得的本征CrSi2介电函数与能量的变化趋势与本文相似，Ti、La掺杂CrSi2的介电常数分别为31.9、91.69，同周期近邻元素的原子半径相似，最外层电子数差值为1，可以看出介电函数的分布与掺杂元素的最外层电子数有关。

2.3.2 吸收系数

图5为未掺杂及Sc、Ce掺杂CrSi2的吸收系数与能量的关系，由图可以分析材料对物质的吸收能力。未掺杂的CrSi2的吸收边约为0.19 eV，相比于本征CrSi2，Sc、Ce掺杂使得CrSi2禁带宽度减小，同时掺杂还引入了杂质能级，因此Sc、Ce掺杂CrSi2的光学吸收边向低能方向移动并扩展至0 eV。本征CrSi2的吸收系数最大值为4.05×105cm-1，位于E=7.46 eV处，Sc、Ce单掺和Sc-Ce共掺CrSi2的第一吸收峰峰值有所减小，依次为：3.94×105cm-1、3.86×105cm-1和3.71×105cm-1，近邻元素Ti、La掺杂CrSi2的吸收系数与能量的关系变化趋势与本文相同，掺杂后出现了一个吸收峰，峰值为：1.42×105cm-1、3.38×105cm-1，与未掺杂前计算本征CrSi2的4.0×105cm-1、4.01×105cm-1相比也有所下降，未掺杂前的第一吸收峰与本文的计算结果4.05×105cm-1近似。相比于Ti、La掺杂后出现的一个吸收峰，掺杂Sc和Sc-Ce共掺后在能量为30 eV附近出现第二吸收峰，同时掺杂Sc、Ce及Ti、La后的CrSi2吸收峰均向低能方向移动。E<21.6 eV时，掺杂体系与本征CrSi2吸收系数与能量的关系变化趋势基本相同，随着能量的增加，吸收系数先上升后下降，但与Sc、Ce掺杂后的CrSi2不同，本征CrSi2在E=2.42 eV处有一个小峰。在E>21.6 eV的较高能区，Sc掺杂和Sc-Ce共掺CrSi2的吸收系数随着能量的增加而有所上升，并在E=31.3 eV附近形成了第二个峰值，而在能量大于21.6 eV且小于31.3 eV时，未掺的CrSi2几乎不吸收光子。Sc、Ce单掺和Sc、Ce共掺CrSi2吸收光子的能力增强，在该能量处Sc-Ce共掺后的CrSi2吸收系数最大。以上结果表明：掺杂体系在小于4.90 eV的和大于21.6 eV范围能区内吸收光子的能力强于本征CrSi2。

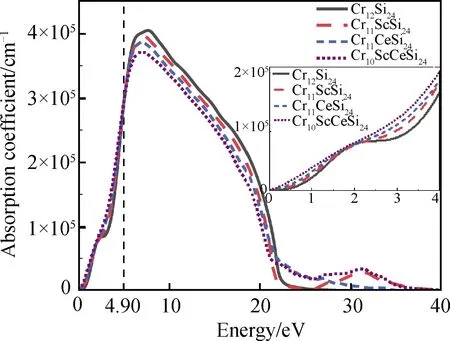
图5 未掺杂及Sc、Ce掺杂CrSi2的吸收系数与能量的关系Fig.5 Relationship between absorption coefficient and energy of undoped and Sc or Ce doped and co-doped CrSi2

2.3.3 光电导率

图6为未掺杂及Sc、Ce掺杂CrSi2的光电导率实部。在小于5.10 eV的低能区，未掺杂的CrSi2光电导率实部的值随入射光子能量的增大而增大并在E=5.10 eV处出现第一个尖峰其值为17.45 fs-1，达到峰值后，在E<42.16 eV之前其光电导率随能量的增加而减小直到趋于零，而后继续上升并在44.15 eV处达到第二峰其值为4.37 fs-1。在20.01 eV

图6 未掺杂及Sc、Ce掺杂CrSi2的光电导率与能量的关系Fig.6 Relationship between photoconductivity and energy of undoped, Sc or Ce doped and co-doped CrSi2

Sc、Ce单掺和两元素共掺CrSi2的光电导率第一峰峰值高度依次减小，分别为16.34 fs-1、15.73 fs-1、14.46 fs-1，同时峰值向低能区移动。与本征CrSi2相比，虽然掺杂后的CrSi2光电导率第一峰峰值有所减小，但在小于3.91 eV的低能区掺杂后的CrSi2光电导率高于本征CrSi2，表明Sc、Ce掺杂特别是Sc-Ce共掺后增强了CrSi2在低能区的光响应。在20.01～34.21 eV的能量范围内，Sc、Ce单掺和Sc-Ce共掺CrSi2的光电导率均大于未掺杂的CrSi2且依次增大。

3 结 论

本文以CrSi2为基本模型，选用过渡金属元素Sc、稀土元素Ce取代CrSi2晶胞中的Cr原子。采用基于密度泛函理论的第一性原理方法，对未掺杂及Sc、Ce掺杂CrSi2的几何结构、电子结构和光学性质进行了计算，结果表明：

(1)与Cr原子相比，Sc和Ce原子半径较大，Sc、Ce掺杂CrSi2后其晶格常数和晶胞体积增大。

(2)与本征CrSi2相比，掺杂体系的带隙均变小。Sc、Ce单掺CrSi2的费米能级向低能区的价带移动并与价带产生交叠，价带顶部越过费米面。由于Sc-3d、Ce-4f态电子的主要影响，掺杂体系的禁带中都出现了杂质能级。Sc、Ce掺杂的CrSi2呈金属性，导电能力提升明显。

(3)Sc、Ce掺杂CrSi2的复介电函数虚部第一峰峰值增大，并向低能方向发生红移。在小于1.64 eV的低能区和在能量大于2.23 eV且小于4.13 eV的范围内，掺杂后的CrSi2体系光跃迁强度增强，提升最大的是Sc-Ce共掺的CrSi2。由吸收谱可知，在大于21.6 eV的区域，本征CrSi2几乎不吸收光子，表现为金属反射的特性，而掺杂后的CrSi2能对光子进行有效的吸收，改善了本征CrSi2在高能区的光学性质。在小于4.90 eV的较低能区，掺杂后的CrSi2的吸收系数大于本征CrSi2，Sc、Ce掺杂CrSi2后其对红外光子的吸收有所改善。Sc、Ce掺杂后的CrSi2光电导率第一峰值有所下降，在小于3.91 eV的低能区间以及20.01～34.21 eV的范围内，Sc、Ce掺杂CrSi2的光电导率大于本征CrSi2，其中Sc-Ce共掺的CrSi2在该区间光电导率最大。以上表明Sc、Ce掺杂能有效改善CrSi2的光学性质。