立足教材 回归课本——基于“读”“探”“升”维度探寻高三数学复习路径

谢梓璋

（南安第一中学，福建 泉州 362300）

课本是教师教和学生学的载体.课本上的例题、习题更是经过精选、具有很强的代表性的，它不仅是教师施教、学生学习的主要材料，也是高考命题的重要取材途径之一.面对扑面而来的各式各样的复习材料，教师要对高三数学复习负起责任，要重视引导学生回归课本，认真钻研教材，拓展其教育功能.本文试析通过“读”“探”“升”三个维度，深究课本上的典型例题与习题本源，提升总复习有效.

一、“读”——课本经典例题再读

课本的一些例题、习题富有代表性、思想性，是复习的良好载体，值得学生回归再读.这类例题、习题在各个模块都有，高三年复习时，教师可结合复习进度，向学生明确要求哪些例题、习题需要再读、再做.当然，为了检测提升学生再读、再做的成效，教师要做一定的引导，避免学生只是简单的“重复”.

例1（人教A 版必修4 第39 页例5）.“求函数y=，x∈[-2π,2π]的单调递增区间.”

①抛出原题，让学生“新”做，检测学生是否“看”了；

②解法新：你还有其他解法吗？检测学生是否“思”了；

③条件新：若把x∈[-2π,2π]改为x∈[0,4π]呢？若是求单调递减区间呢？检测学生是否“懂”了.

单调性是三角函数的重要性质，也是重要考点之一.本例5 主要通过化归方法并利用正弦函数的单调性进行求解，在三角函数的学习中有着重要的教育价值，一是它揭示了三角函数性质研究的范式（变量代换、化归、数形结合），二是可生成性强（如可改变区间大小，或是改变问法，如拓展为求“最值问题、不等式问题”等），值得学生“再读”、感受经典.高三年复习时，“再读”课本经典例题（建议适当改变问题呈现形式），可以在较短的时间内实现对解题范式、解题策略进行归纳总结，不失为一种高效、接地气的复习方法.

二、“探”——不同问题不同变式探究

（一）对比与比较：建立知识的合理联系与区别的变式

对例题、习题进行归类整理，观察共性和个性，发现它们之间共同的本质属性或解题规律，这是培养学生数学核心素养，提高解题能力的重要途径之一.

例如，圆锥曲线之间很多知识可以进行类比、探究，值得师生研究.

例2（人教A 版选修2-1 第55 页探究）.如图1，设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M，且它们的斜率之积是，求点M的轨迹方程并由点M的轨迹方程判断轨迹的形状，与P412.2 例3 比较，你有什么发现？

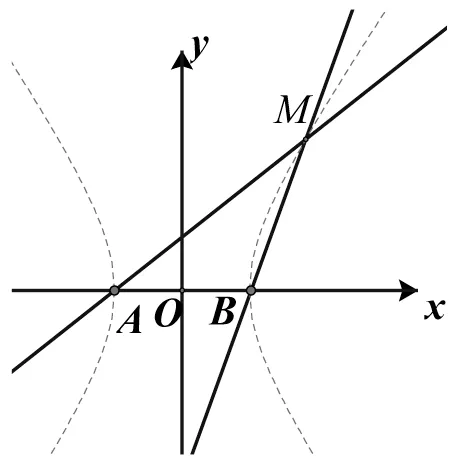
图1

教学中教师可以此为契机，引导学生进一步思考斜率之商（和、差）为定值的轨迹问题，详见教材P42练习4 的“斜率的商”、P74B 组题3 的“斜率的差”、P81B 组题5 的“斜率的和”.

教材对于三种圆锥曲线的定义都是立足“距离”间的关系给出，本例则从“角度”间的关系反映圆锥曲线的性质.复习中，教师若能通过对斜率之积（商、和、差，即四则运算）为定值情形的进行对比与比较，不仅可以帮助学生形成解析几何研究问题的一般方法：数学问题→代数问题→方程求解，加深对“坐标法”的理解，而且可以渗透学习方法的指导——“类比”是圆锥曲线的重要学习方法.当然，教师还可启发学生逆向思考问题，获得圆锥曲线的一条性质：椭圆、双曲线上的点【长轴（或实轴）端点除外】与长轴（或实轴）的两个端点连线的斜率之积是定值，同时，这条性质可以进一步推广.

可见，教师引导学生对教材的例题、习题进行适当的对比与比较，不仅可以对相关知识进行梳理，而且能够较好实现“多题一法”，形成此类问题的“解题范式、解题策略”，提升复习的实效性.

（二）延伸与拓展：由点到面、拓展推广引发的变式

高三复习中，不仅要有横向的深入，更需要有纵向的联系组合、类比、沟通知识联系，实现知识由“厚”到“薄”、由“散乱”到“有序”的转化，实现“一个”问题到“一类”问题的转变.

例3（人教A 版选修2－1P73A 组第6 题）.如图2，直线y=x-2 与抛物线y2=2x相交A,B两点，求证：OA⊥OB.

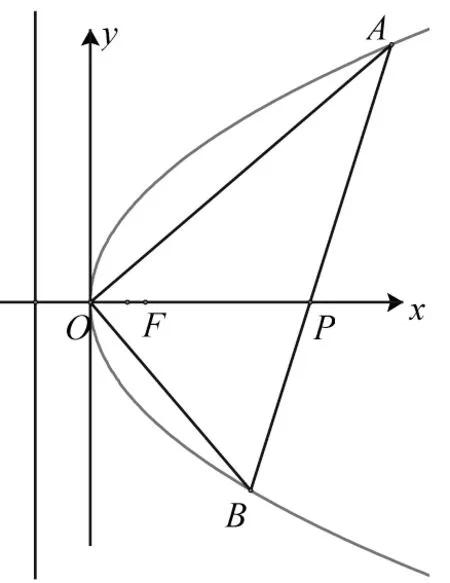
图2

①逆向思考

抛物线y2=2x上不同两点A,B，若满足OA⊥OB，则直线AB是否恒过定点？（经验证，直线AB经过定点（2，0）.（过程略）

②逆向推广

设直线l与抛物线y2=2px(p＞0)交于不同两点A,B，若满足OA⊥OB，则直线l恒过定点P(2p,0).…………（*）

略证：由条件可知直线AB的斜率不为0，可设直线AB：x=my+b(b≠0)，代入y2=2px得：y2-2pmy-2bp=0，∴y1+y2=2pm,y1y2=-2pb.

若OA⊥OB，则容易求得=-2pb+b2=0.∵b≠0,∴b=2p，∴直线AB：x=my+2p，即直线AB恒过定点P(2p,0).

③延伸拓展

如：在平面直角坐标系x0p中，直线l与抛物线y2=2x相交于A,B两点.

（I）求证：“如果直线l过点T(3,0)，那么=3”是真命题；

（II）写出（I）中命题的逆命题，判断它是真命题还是假命题，并说明理由.

根据以上的思考，不难判断（I）中命题的逆命题是假命题.

④类比迁移

结论(*)是否可以类比到椭圆？

过抛物线y2=2px(p＞0)的顶点O作两条互相垂直的直线，分别交抛物线于另外两点M.N，则直线MN过定点P(2p,0).类比此命题，写出关于椭圆1(a＞b＞0)的一个真命题：____

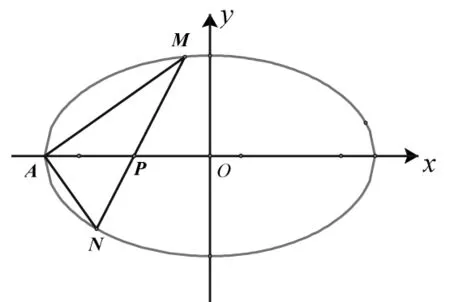
图3

⑤以点带面

从问题①②③④的解决，我们可以发现，解决问题OA⊥OB，往往可以转化为研究可见，转化与化归思想是解析几何常见的解题思想.为此，在复习时，要注重培养学生的转化意识，比如，数量积型的转化：⇔点O在以AB为直径的圆上；点O在以AB为直径的圆外（圆内）⇔∠AOB为锐角（钝角）.

《普通高中数学课程标准（2017 版）》明确指出，数学教学要发展学生的数学学科核心素养.显然，围绕碎片化的知识点，以“知识点讲解+例题+练习”的方式设计教学活动，已经无法承载数学基本思想和基本活动经验教学的要求，对核心素养发展不利.采用“由点到面、拓展推广”的变式探究，可以在较大程度上缓解“知识点讲解+例题+练习”带来的弊端，避免“就题论题”“只见树木，不见森林”的局限性，可以较好实现知识间的融会贯通、知识网络的构建，引导学生实现“有联系”的数学思考.

（三）思想与方法：由核心思想、方法引发的变式

回归课本不能仅仅只是停留在表面上，而应该对课本上的数学知识与隐藏其中的数学思想方法加以总结提高，加工成“串”，使知识“升华”，从而达到知识的融会贯通，体会数学内涵，领悟数学核心思想.

例如，三角函数的单位圆定义是三角函数的核心内容，复习时，

首先要引导学生理清两条主线：

一是计算主线：单位圆定义→三种三角函数的值在各象限的符号判断→同角三角函数的基本关系式→诱导公式；

二是图象主线：单位圆定义→三角函数线→三角函数的图象.

其次，要强化单位圆定义的应用：

一是单位圆上点的坐标表示.

二是定义的直接应用.

例4（人教A 版必修4 第59 页B 组3）.如图4，点P是半径为rcm 的砂轮边缘上的一个质点，它从初始位置P0开始，按逆时针方向以角速度wrad/s做圆周运动.求点P的纵坐标y关于时间t的函数关系.（由sin ∠xOP=sin(wt+φ)=有y=rsin(wt+φ).

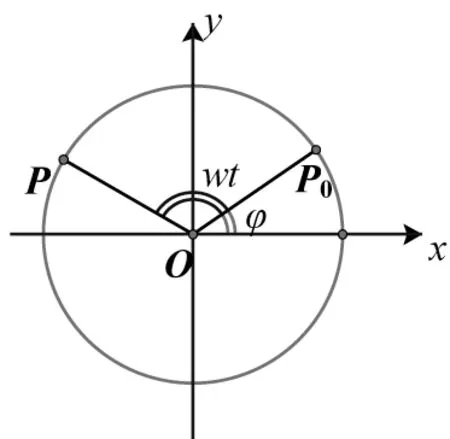
图4

相比陈述性知识而言，数学思想方法是“活”知识，是数学知识在更高层次上的抽象与概括，它蕴含在数学知识发生、发展和应用的过程中.对于解题，数学思想方法就是解题的策略、指导思想，是能实现知识的迁移和转换，是创造性思维的基础.高三年复习，教师要注重引导学生对数学思想方法进行梳理与总结、提炼，认识它们的本质特征，自觉、灵活地加以应用.比如，在本例4 中，教师要注意引导学生挖掘解题的数学本质——三角函数的定义（思考：如何建系、设角、定义表达），这样在“水车”“摩天轮”等问题中，学生就容易实现知识的迁移.

值得注意的是，核心思想方法的渗透贵在立足平常教学.比如，“坐标法”是解析几何的核心思想，“设而不求”“转化与化归思想”是求解直线与圆锥曲线问题的重要思想，“空间问题平面化”“降维”是解决空间立体几何的重要思想等等，这些都需要平时教学的渗透，方能被学生所内化.

三、“升”——改进提升教材不尽完美之处

“智者千虑，必有一失”，教材不可能十全十美！师生分析、处理教材时，要敢于大胆质疑，对教材中不够规范、不够简洁的地方进行改进，使教材更好地发挥教学的基本素材作用.

例5（人教A 版必修5 的第14 页的例5）.如图5，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧远处一山顶D在西偏北15°的方向上，行驶5km后到达B处，测得此山顶在西偏北25°的方向上，仰角为8°，求此山的高CD.

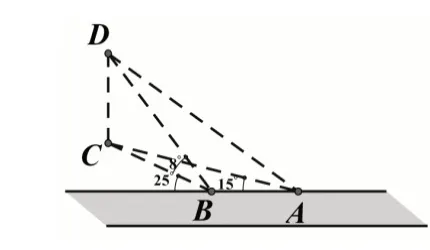
图5

这是有关测量底部不可到达的建筑物的高度问题，立意很好，回归再读课本时，笔者发现学生不甚理解，究其原因，原来是弄不清角度之间的关系.而其根本原因在于题目的分析不到位（应明确指出本题是属于空间几何中的三角形问题）、况且图画得不好.为此，笔者以生活情境为入口，理清条件之间（特别是角度）的关系，同时，与学生共同把图形画好（如图6），突出平面ABC，方便学生的理解.

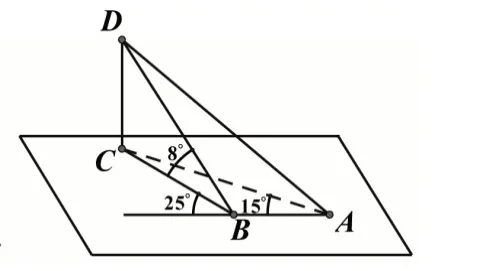
图6

普通高中数学课程标准（2017 版）明确指出，要开展独立思考、自主探究、合作交流等学习活动.步入高三年复习，学生由于知识储备量的增加，对问题的看法也就更加丰富.此时，教师可以因势利导，引导他们对一些重要的数学概念、定理、公式、例题、习题等重新审视，鼓励他们提出不同见解、不同解法，形成不同解决方案，同时，教师要及时做出积极的评价.如此回归课本，学生获得不仅是新鲜感，而且是成就感，再有的是满满的自我内驱力.