基于余弦相似度的改进蝴蝶优化算法

陈 俊，何 庆

（贵州大学大数据与信息工程学院，贵阳 550025）

（*通信作者电子邮箱qhe@gzu.edu.cn.）

0 引言

近些年，许多学者受到自然界动物习性的启发，对自然界生物种群所表现出群体性行为进行总结，设计出一类具有分布式智能行为的算法（群智能优化算法）。这类优化算法对目标函数性质要求低、容易实现、稳定性好，自提出以来就受到电力系统、工程设计，网络以及通信等领域的广泛关注。

常见的群智能优化算法有：模拟果蝇靠嗅觉定位食物方向行为提出的果蝇优化算法（Fruit fly Optimization Algorithm，FOA）［1］；模拟布谷鸟寄生育繁殖行为和莱维飞行搜索机制的布谷鸟搜索（Cuckoo Search，CS）算法［2］；通过模拟鲸鱼随机搜索扑食，气泡攻击，收缩包围行为的鲸鱼优化算法（Whale Optimization Algorithm，WOA）［3］等。

2017 年，Arora 等［4］受到蝴蝶觅食行为的启发，提出了蝴蝶优化算法（Butterfly Optimization Algorithm，BOA）。蝴蝶个体通过感知和分析空气中气味确定食物的潜在方向，进行合作式的移动。相较于其他的群智能优化算法，蝴蝶优化算法具有结构简单、控制参数少以及算法易实现的特点，在工程上得到广泛的应用。例如张达敏等［5］将改进的蝴蝶优化算法应用于认知智能电网中的能效优化频谱分配上；Wen 等［6］提出一种增强的蝴蝶优化算法，并将改进的蝴蝶优化算法应用于支持向量机参数优化上，最后还预测了长三角地区住宅的二氧化碳年排放量；Malisetti 等［7］提出一种基于对抗的蝴蝶优化算法，并应用于无线传感器的方案选择，延长了无线传感器网络的使用寿命。与其他群智能优化相比，虽然蝴蝶优化算法在设计上具有优越性，但是该算法依旧存在寻优精度低、收敛性差以及易受到局部极值影响的问题。

针对以上问题，许多学者对蝴蝶优化算法进行改进，Arora 等［8］提出了一种基于莱维飞行策略的蝴蝶优化算法，在全局和局部位置上引入莱维函数，增强了算法种群的多样性。Arora 等［9］还提出了一种基于学习自动机的蝴蝶优化算法，通过引入学习自动机策略，提高了全局阶段的搜索速度。王依柔等［10］提出了基于自适应扰动的疯狂蝴蝶算法，在全局搜索阶段引入自适应惯性权重和扰动策略，避免蝴蝶优化算法易陷入局部最优的同时平衡了算法的局部开发和全局探索能力，最后还在花蜜位置上引入疯狂因子，增强了蝴蝶种群的多样性。高文欣等［11］提出柯西变异和自适应权重优化的蝴蝶算法，通过在全局位置更新上引入柯西分布函数对蝴蝶个体进行变异，解决了算法容易陷入局部最优的问题，其次在局部开发位置更新处引入自适应惯性权重，加强了蝴蝶算法的局部开发能力；最后还引入了动态转换概率来平衡算法的全局探索和局部开发的比重。谢聪等［12］通过参数优化和差分进化两个角度提升了算法性能，首先针对蝴蝶优化算法内感知强度参数和感觉因子进行微调，优化了算法内参数；其次引入了差分进化策略，加强了蝴蝶个体之间信息交流能力。高文欣等［13］提出了全局优化的蝴蝶优化算法，通过引入limit 阈值来限制蝴蝶优化算法陷入局部最优解的次数，解决蝴蝶优化算法易陷入早熟的问题；其次融合了单纯刑法策略，使得适应度较差的蝴蝶个体也能较快靠近当前最优蝴蝶个体。上述改进策略虽然在算法的种群多样性上有一定程度的提升，但没有解决算法在迭代中后期种群多样性下降的问题；而且部分策略调整了蝴蝶优化算法中全局探索和局部开发的转换概率，并没有充分利用蝴蝶个体信息动态调整转换概率。

针对上述的问题，本文提出了一种多策略改进的蝴蝶优化算法（Multi-Strategy improved BOA，MSBOA）。首先，提出了基于余弦相似度的位置更新策略，通过构建当前蝴蝶个体位置到最优蝴蝶位置的向量，计算向量之间的余弦相似度，并设置阈值，更新余弦相似度超过阈值的蝴蝶个体，该策略能有效地保持了种群的多样性；其次，根据蝴蝶个体的适应度动态调整转换概率，使适应度较差的个体有更大的概率受到最优蝴蝶个体的引导，加快BOA 收敛；最后，在全局搜索阶段加入自适应混合惯性权重，根据蝴蝶个体自身适应度动态平衡当前个体的局部开发与全局探索能力。通过对16 个典型的测试函数的求解、Wilcoxon 秩和检验以及部分CEC2014 函数的求解验证了MSBOA的有效性和鲁棒性。

1 蝴蝶优化算法

蝴蝶优化算法是Arora 等［4］通过观察蝴蝶觅食和寻偶行为提出的一种新的群智能优化算法。由于真实的蝴蝶觅食和寻偶行为有很多不确定的因素，无法在算法中体现出来，因此蝴蝶优化算法建立在两个理想化的条件下：1）假设每只蝴蝶都能产生不同程度的香味并且能嗅到来自不同方向的香味，使得蝴蝶个体之间能够相互吸引。这种香味的强度与蝴蝶个体的适应度有关，用于在蝴蝶迭代过程中分享自身的相关信息。2）每只蝴蝶都有一定的概率嗅到来自最优蝴蝶个体的香味并朝向最优蝴蝶位置方向移动，该行为称为全局探索。其中该概率在蝴蝶优化算法中称为转换概率。若蝴蝶嗅不到来自最优蝴蝶个体的香味，蝴蝶个体将随机移动，这一行为称为局部开发。其中转换概率P的大小受到风雨雷电等各种情况的影响，全局探索和局部开发的转换概率P值取固定值0.8。

蝴蝶产生香味强度大小表达式如下：

其中：f是香味的感知强度，即香味被其他蝴蝶感知的强度；I是刺激强度，取值大小与当前个体适应度有关；a取固定值0.1，通常参数a的取值取决于模态的功率指数。c是感觉因子，数学模型描述如式（2）所示：

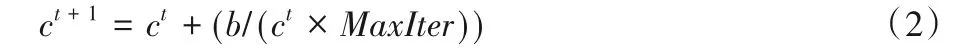
其中：ct+1是t+1次迭代群体的感知因子；ct是t次迭代中的感知因子；b通常取固定值0.025；MaxIter是最大迭代次数。每一次迭代生成一个区间为［0，1］的随机数与转换概率P进行比较，若随机数小于转换概率P，BOA 进行全局搜索，反之进行局部搜索。

全局搜索阶段，蝴蝶朝向最优蝴蝶位置移动，数学模型如式（3）所示：

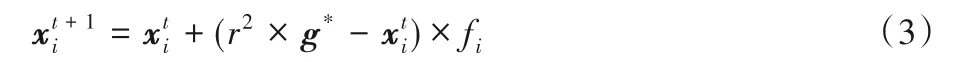
其中：是第t次迭代中第i只蝴蝶的解向量；r是区间［0，1］内的随机数；g*表示在当前迭代的所有解中的最优位置；fi表示第i只蝴蝶发出的香味强度。

在局部搜索阶段，蝴蝶将随机移动，蝴蝶位置更新公式为：

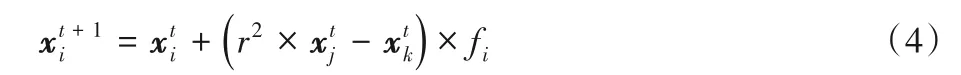
2 本文算法MSBOA

根据BOA 的设计可知，每只蝴蝶个体都要受到当前最优蝴蝶个体的香味吸引进行移动。该机制虽然一定程度上矫正蝴蝶位置更新的方向，但是在迭代中后期，蝴蝶个体聚集到当前最优蝴蝶位置附近导致蝴蝶种群的多样性会下降，若当前最优蝴蝶个体陷入局部最优，聚集的蝴蝶种群很难跳出局部极值点。其次采用固定概率为0.8 的两段式更新策略，使得大部分的蝴蝶个体围绕着全局探索的更新方式，更多时候接收全局最优位置信息。由于BOA 这两个特征，使得在迭代后期种群的多样性下降，甚至出现多个蝴蝶位置重叠的情况，从而导致BOA容易陷入局部最优且收敛精度较低。

为了解决以上BOA 的问题，本文提出MSBOA。本文从3个方面对BOA 进行改进。首先是基于余弦相似度的蝴蝶位置更新策略，取当前蝴蝶位置和当前最优蝴蝶位置构建向量，依次计算向量之间的余弦相似度，并通过设置阈值C，将余弦相似度大于阈值的蝴蝶个体与当前蝴蝶个体进行适应度比较，通过位置更新策略更新适应度较差的蝴蝶个体，解决迭代后期算法种群多样性下降的问题；其次通过适应度动态调整切换概率，使得适应度较好的个体有更大的概率进行全局引导；最后引入混合自适应惯性权重策略，较大的权重能使BOA保持较好的全局探索能力，较小的惯性权重有助于BOA 局部开发，根据蝴蝶个体的自身适应度以及迭代情况动态平衡BOA搜索偏向。

2.1 基于余弦相似度位置更新策略

余弦相似度反映两个向量方向一致性关系，取值范围为［-1，1］，其中：1 表示两个向量之间的夹角为0°，有重合部分；-1 表示两个向量方向相反。由于BOA 的特点，在迭代中后期，蝴蝶移动围绕当前最优蝴蝶位置，甚至于移动过程中出现重叠的现象，很难保持种群多样性。本文引入余弦相似度衡量最优蝴蝶位置与周围蝴蝶的分布情况，通过构造当前蝴蝶个体位置和最优个体之间的向量，采用余弦相似度作为分布情况的指标，更新余弦相似度较高且适应度较差的蝴蝶个体位置，既提高算法收敛的速度，又保持了种群的多样性。策略具体细节如下：

首先构建a、b向量：

其中：表示在第t次迭代中第i只蝴蝶的个体，即当前蝴蝶位置；表示第t次迭代其他蝴蝶个体中的一个；g*属于第t代中的最优蝴蝶个体的位置。

定义cos（ja，b）为两个向量之间的相似度，取值范围为［-1，1］，个体位置之间相似度计算公式为：

其中：分子为向量a、b的内积，分母分别为向量a、b的模的积。余弦相似度越高，代表蝴蝶个体和越容易在方向上重合。将当前蝴蝶位置i与其他蝴蝶位置j依次计算余弦相似度，并设置阈值C，将与当前蝴蝶位置余弦相似度较高的蝴蝶进行筛选，经多次调试，当C取0.5 时，算法性能达到最优。通过比较当前蝴蝶个体与筛选后个体的适应度，将适应度较差的个体引入状态转移算法中的旋转变换算子或伸缩变换算子［14］进行位置更新，并保留适应度较好的蝴蝶个体位置，位置更新公式如下：

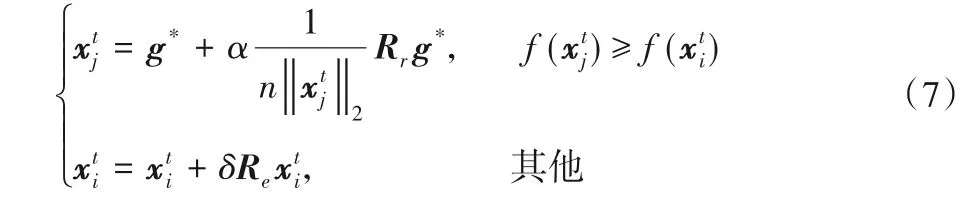
2.2 根据适应度动态调整转换概率策略

在基本的BOA 中，切换概率P，使用固定的常数来调整BOA的局部开发和全局探索。本文采用文献［15］提出的自适应机制来描述切换概率，并且作了改进。如式（8）所示：

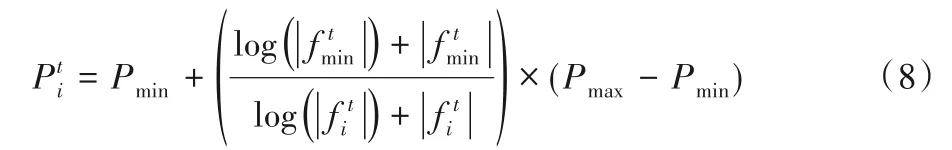
2.3 自适应混合惯性权重

本文还在全局搜索阶段当前个体的位置更新式（3）中引入动态惯性权重w来影响更新蝴蝶的位置，惯性权重较大或者较小都有可能引起BOA 陷入局部最优，从而影响BOA 的效率。为了协调BOA 的全局和局部搜索能力，本文提出了自适应混合惯性权重：

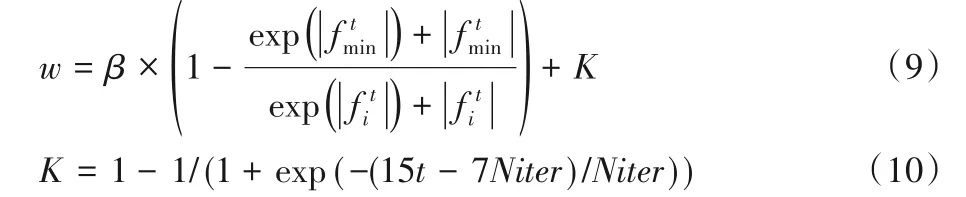
其中：K为是调整过的sigmoid函数，该函数是神经网络中最常用的激活函数之一。该函数在线性和非线性之间展现出极好的平衡性，拥有平滑的上界域和下边界域。在迭代前期参数K能保持较大值，保持蝴蝶优化算法在迭代初期阶段的全局搜索强度；并且前期K值伸缩的范围较大，更好地保留了BOA的多样性。中期K值随着迭代次数的增加而减少，从而加快BOA 的收敛。在迭代后期的一段保持一个较小的权重，延长了迭代后期的局部搜索时间，更有利于进行局部搜索，更新后的全局阶段搜索过程为：

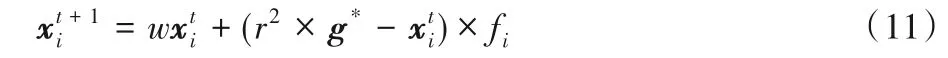
权重引入了式（9）的一部分，其目的在于控制最优蝴蝶位置对新的蝴蝶位置的影响程度，参数β为影响程度因子。蝴蝶个体适应度接近当前最好的适应度时，其权重接近最小值，较小的权重有利于进行局部开发；反之当前个体的适应度与最好的适应度相差较大时，其权重接近最大值，保留当前个体的更多信息，下一次迭代保持较强的全局搜索能力。

2.4 MSBOA步骤

MSBOA的基本流程如下：

Step1 初始化。初始化MSBOA 参数，随机生成种群位置，计算适应度并择优保存。

Step2 蝴蝶位置更新阶段。根据式（5）构建向量，并根据式（6）计算蝴蝶个体位置的余弦相似度，设置阈值C将相似度高于阈值的蝴蝶位置通过式（7）进行位置更新。

Step3 计算当前个体适应度，并根据式（8）计算P值，判断当前迭代当前个体是进行全局搜索还是局部搜索，并通过式（10）计算当前个体的自适应惯性权重，对应蝴蝶位置的更新式（11）或式（4）。

Step4 计算位置更新后每只蝴蝶所在位置适应度，并且更新最优位置。

Step5 重复Step2～4 的更新迭代过程，若达到设置收敛精度要求或规定的最大迭代次数，终止MSBOA 并输出最优解。

MSBOA流程如图1所示。

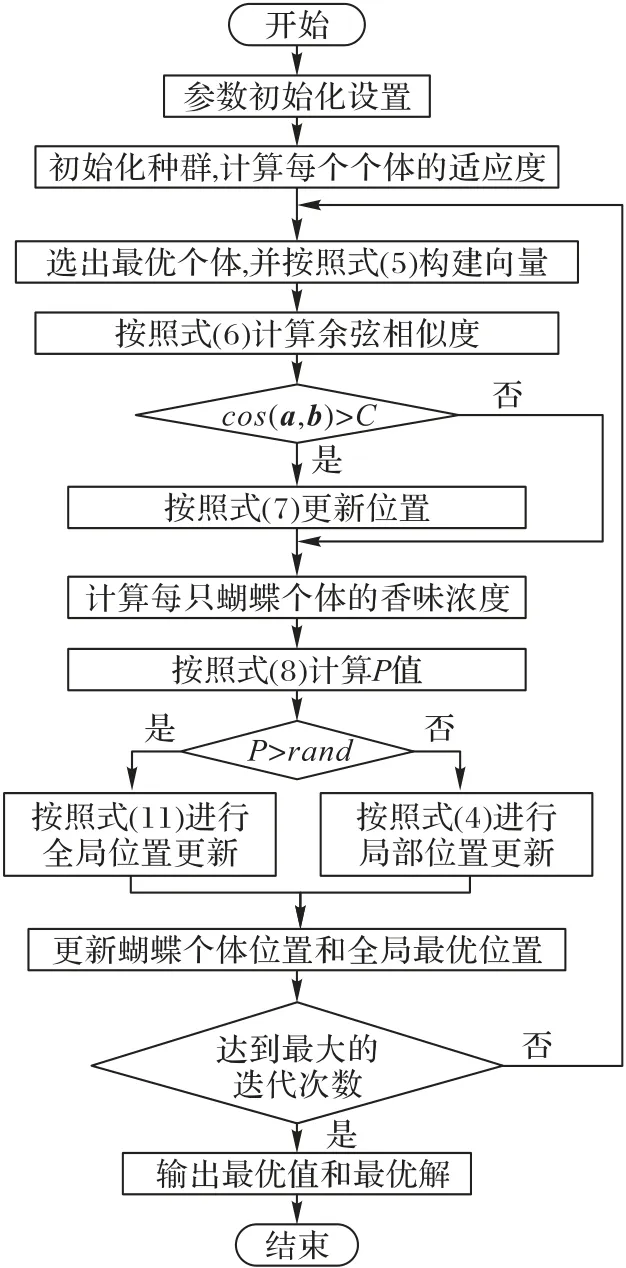
图1 MSBOA流程Fig.1 MSBOA flowchart

2.5 MSBOA的时间复杂度分析

时间复杂度是体现算法的性能的关键因素，反映了算法的运行效率。通过阅读文献［16］和文献［13］对混合柯西变异和均匀分布的蝗虫优化算法和全局优化的蝴蝶优化算法（Simplex Method Sine-Cosine Algorithm Butterfly Optimization Algorithm，SMSCABOA）的时间复杂度进行了分析方式。本文拟采用了类似的方式对MSBOA进行时间复杂度分析。

在基本的BOA 中，假设种群的规模为N，空间维度为n，最大迭代的次数为MaxIter，计算适应度函数时间复杂度为（fn）。根据算法时间复杂度（O）的计算规则。则有：

1）种群初始化阶段，假设参数初始化所需要的时间为x1，初始化一个个体位置需要的时间为x2，则产生随机初始化种群位置的时间复杂度为O（x1+x2×N×n）=O（N×n）。

2）找到当前最优蝴蝶位置的时间复杂度为O（N×（fn）），此时的时间复杂度为O（N×n+N×（fn））。

3）基于余弦相似度位置更新策略的时间复杂度计算分为两个部分，分别是计算蝴蝶个体之间的余弦相似度和位置更新算子的时间复杂度。其中构建向量部分需要的时间复杂度为O（N×n）；计算蝴蝶个体之间的余弦相似度需要的时间复杂度为O（（N-1）×n）=O（N×n）；进行位置更新的时间复杂度最大也是O（N）级别的时间复杂度。则该部分的时间复杂度为O（N×n）。

4）根据适应度动态调整转换概率策略，对单个体在一次迭代中增加的时间复杂度为O（1+（fn））=O（（fn））。

5）在自适应混合权重阶段，参数大多数是继承目前已存在的，在原本基础上对个体增加的时间复杂度也是O（1）级别。

第2）～5）阶段均是单个个体在一次迭代中产生的时间复杂度。当以N个体进行MaxIter次迭代时，MSBOA 在2）至5）阶段的时间复杂度为O（MaxIter×N×（fn）×n）。

综上，MSBOA 的总的时间复杂度为O（N×（fn）+MaxIter×N×N×n）=O（MaxIter×N×N×n）。MSBOA 与BOA 在时间复杂度上相比，MSBOA 在基于余弦相似度位置更新策略上增加了时间复杂度，相当于在算法内层加了循环。

3 仿真实验与结果分析

为了全面的验证MSBOA 的性能以及3 个改进策略的有效性，本文的验证实验分为以下4个部分进行：

1）将MSBOA 与仅采用基于余弦相似度位置更新策略的蝴蝶优化算法BOA1、仅采用结合动态调整概率策略的蝴蝶优化算法BOA2、仅采用自适应混合惯性权重的蝴蝶优化算法BOA3 以及基本的蝴蝶优化算法BOA 进行比较，来验证不同改进策略的有效性；并将改进算法与PSO、SSA 进行收敛性分析，验证MSBOA的优越性。

2）将MSBOA 与向量粒子群优化（Phasor Particle Swarm Optimization，PPSO）算法［17］、改进的灰狼优化（Improved Grey Wolf Optimization，IGWO）算法［18］、基于对数惯性权重和高斯差分变异的鲸群优化算法（Whale Optimization Algorithm based on logarithmic Inertia weight and Gaussian difference mutation，IGWOA）［19］、优选策略的自适应蚁狮优化（Preferred Strategy self-adaptive Ant Lion Optimizer，PSALO）算法［20］、基于折射反向学习与自适应控制因子的改进樽海鞘群算法（modified Salp Swarm Algorithm based on Refracted oppositional learning and adaptive Control factor，RCSSA）［21］进行比较，验证MSBOA的优越性。

3）通过Wilcoxon 秩和检验验证MSBOA 和其他算法之间的显著性差异。

4）在CEC2014 基准函数中选取部分单峰和多峰，混合和复合类型的函数进行优化测试，再次验证MSBOA的有效性和鲁棒性。

实验引入16 个基准测试函数，分为三类：第一类为单峰基准测试函数，表1 中F1～F6 所示；第二类为多峰基准测试函数，如表1 中的F7～F10 所示；第三类为固定维度的多峰基准测试函数，如表1中的F11～F16所示。

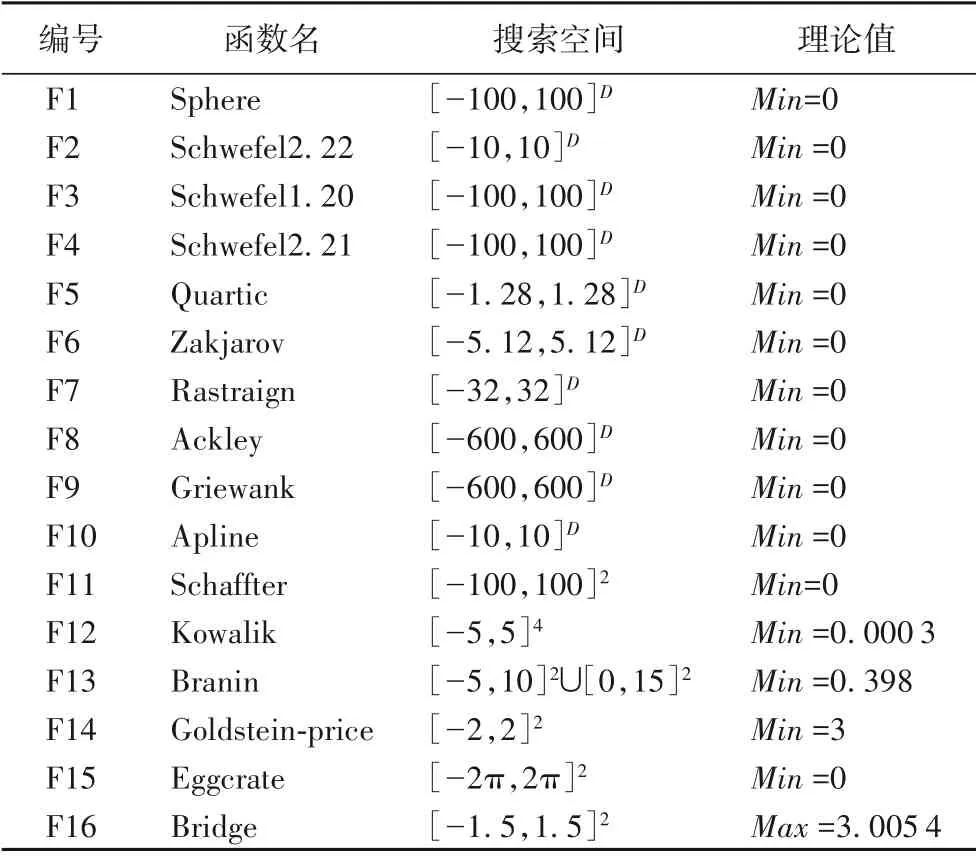
表1 基准测试函数Tab.1 Benchmark test functions

算法的基本参数：种群规模为30，空间维度为30、100、500，MaxIter=500。算法内的参数如表2所示。

表2 算法参数设置Tab.2 Algorithm parameter setting

3.1 改进策略有效性分析

将基本BOA 与BOA1、BOA2、BOA3、MSBOA 在空间维度为30 的条件下对16 个函数进行求解并通过均值以及标准差评估仿真结果，独立运算30次数据进行统计分析，如表3～4所示。首先，表3和表4中的平均值可以反映算法的收敛精度和寻优能力，而标准差可以反映算法的鲁棒性。具体来说，对于单峰值函数F1～F4、F6、F7，以及多峰值函数F9～F11、F13～F16，MSBOA 均可以寻找到理论最优值，且标准差最小；对于函数F5、F8、F12，虽然没有寻到理论最优，但是对于函数F5、F8、F12，无论是平均搜索精度还是稳定性上，MSBOA均体现出明显的优势。在固定维度函数上，MSBOA 的寻优化精度和稳定性也明显好于BOA。单从3 个改进策略上来看，BOA1和BOA3对函数F1～F4以及F5～F15改进效果明显。从评价指标上可以看出BOA1 在无论在单峰函数还是多峰值函数上寻优精度与MSBOA效果持平，这和引入的基于余弦相似度更新策略密切相关，该策略有效地提高了BOA 的寻优能力。BOA2对函数的寻优精度提升幅度不大，在3个改进策略里面相对最差。其中对于F2函数，BOA2收敛精度虽然不及BOA，但稳定性上优于BOA。BOA3 在函数F7、F9 上均能寻到理论最优值，该策略整体效果优于BOA。综合表3 中标准差以及均值上表现，3 个改进策略都在一定程度上提升了BOA 的性能，且融合3 个改进策略的MSBOA 表现出更高的寻优精度以及算法稳定性。

表4 固定维度多峰基准测试函数测试结果Tab.4 Test results of multimodal benchmark test functions in fixed dimension

图2 给出了BOA、BOA1、BOA2、BOA3 以及MSBOA 的单峰和多峰值函数收敛曲线图。如图2 所示，由于MSBOA 收敛精度高，为方便观察算法收敛情况，图2 中纵坐标表示为lg（适应度值）。从图2 可知，在单峰值函数和多峰值函数上，MSBOA 具有更高的收敛速度和寻优精度。具体来说，对于F6、F7、F9、F10 函数，MSBOA 能在200 代能找到最优值，体现出较强的优化能力。从改进策略上来看，BOA1 寻优效果最好，其次是BOA3，BOA2 最差。BOA1 和BOA3 收敛曲线大部分位于BOA 收敛曲线的下方，且收敛较快，这说明引入基于余弦相似度位置更新策略，有效地保持了蝴蝶种群在搜索空间的多样性，使得BOA1 在迭代前期收敛较快，且在多个函数上能找到最优值。在迭代后期，MSBOA 在单峰函数的收敛速度比其他的算法要高，且精度和BOA1 保持一致，这与BOA2和BOA3 密切相关。对于多峰函数，BOA1 和MSBOA 在收敛速度上接近。总体来说，在基准函数上，无论收敛速度还是寻优精度上MSBOA都远远优于BOA。

针对时间复杂度的问题，在1～200 维度上对F1～F10 函数进行仿真实验。从如图3 所示的实验结果来看，与BOA 运行时间相比，改进后算法耗时较长，耗时主要来自于基于余弦相似度位置更新策略。随着维度的增加，在5 种算法的平均耗时上都增加，这是由于从低纬度到高纬度，搜索空间增大，搜索的难度也呈现指数增加。

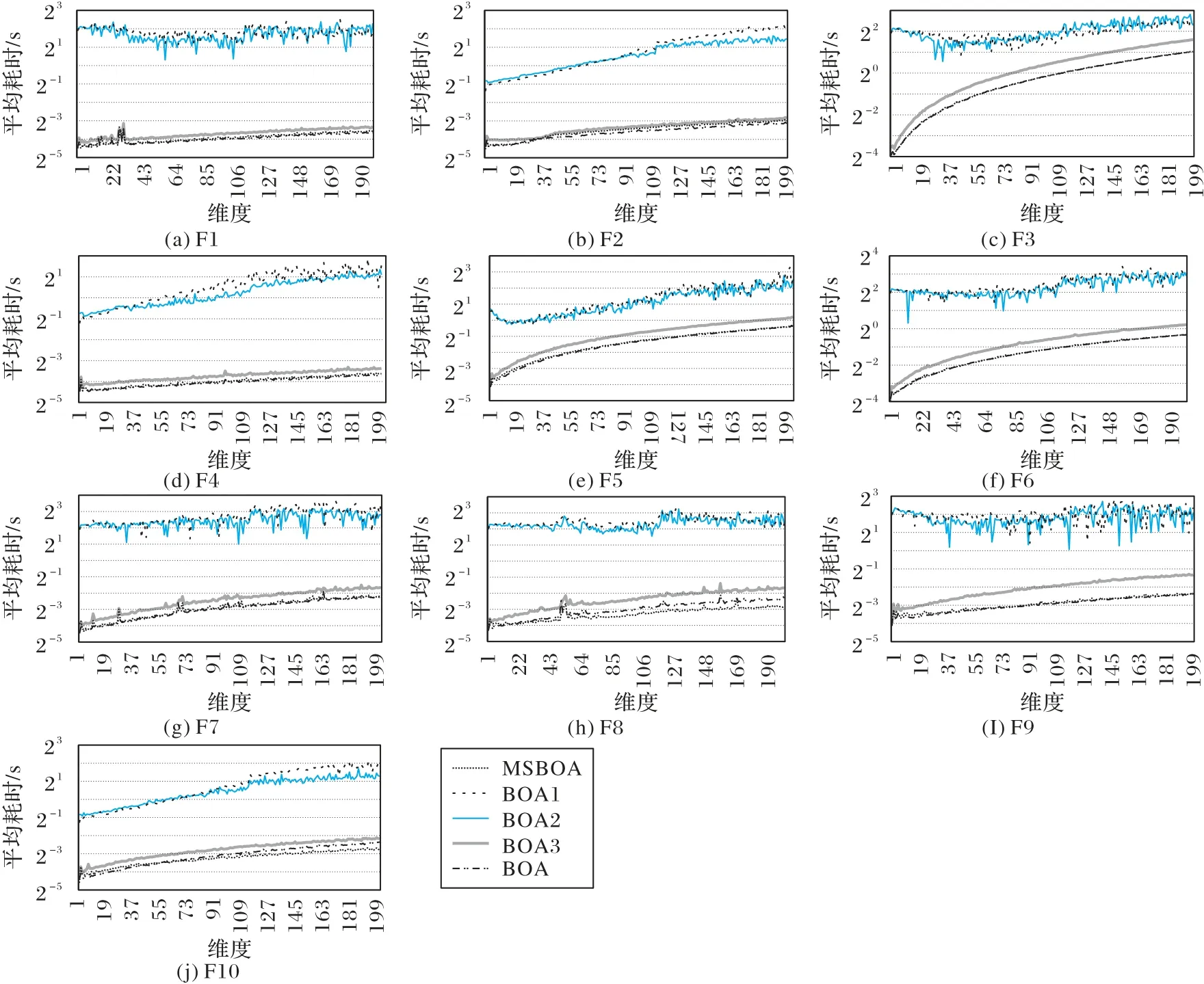
图3 基准函数维度对应平均耗时曲线Fig.3 Curve between benchmark function dimension and average time consumption

从表3～4和图2～3可看出，对MSBOA在寻优精度的表现，验证了有效性，不过耗时相较于BOA有所增加。

表3 单峰和多峰值基准测试函数测试结果Tab.3 Test results of unimodal and multimodal benchmark test functions

图2 基准函数平均收敛曲线Fig.2 Benchmark function average convergence curve

3.2 与其他的群智能算法比较

将MSBOA 与PPSO、RCSSA、IGWO、IGWOA、PSALO 在100 维度的条件下进行对比。对比数据直接引用文献［17-21］，且MSBOA 内参数与表2 保持一致，最大迭代次数和种群个数与对比算法保持一致。在100维度的条件下运行50次取平均值的实验结果如表5所示。

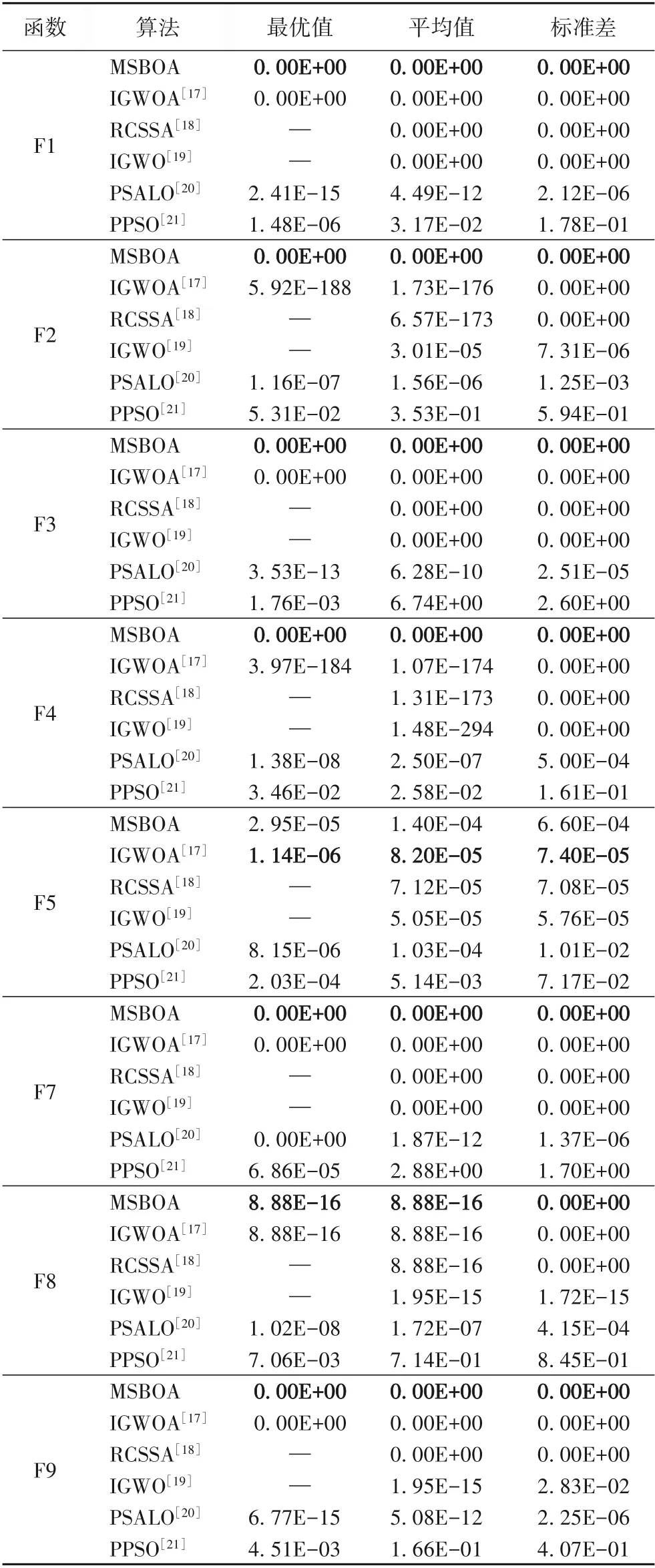
表5 不同群智能算法在100维度下的结果比较Tab.5 Result comparison with different swarm intelligence algorithms in 100 dimensions

表5中的最优值和平均值反映算法的寻优能力。MSBOA对于给定的5 个单峰值函数，其中有4 个能找到理论最优值，并且稳定性优于其他算法。MSBOA 对单峰函数F5 最优值与其他对比算法相比在最优值上相差一个数量级。在3 个多峰值函数，MSBOA在能找到两个函数的理论最优值。在求解F8时，MSBOA、IGWOA 以及RCSSA 寻优精度持平，PSALO 次之，PPSO 效果最差；在平均值和标准差上，MSBOA 比其他算法的表现更好；在求解其他函数时，MSBOA 比其他的算法求解精度都要高且效果稳定。

为了进一步说明MSBOA 的有效性，在相同的实验环境下，将MSBOA 与其他改进的BOA 进行对比，引用CIBOA［10］、CWBOA［11］、SMSCSABOA［13］，以及SIBOA［22］数据，分别在30 维度、100 维度和500 维度上对8 个基准函数进行对比，如表6所示。

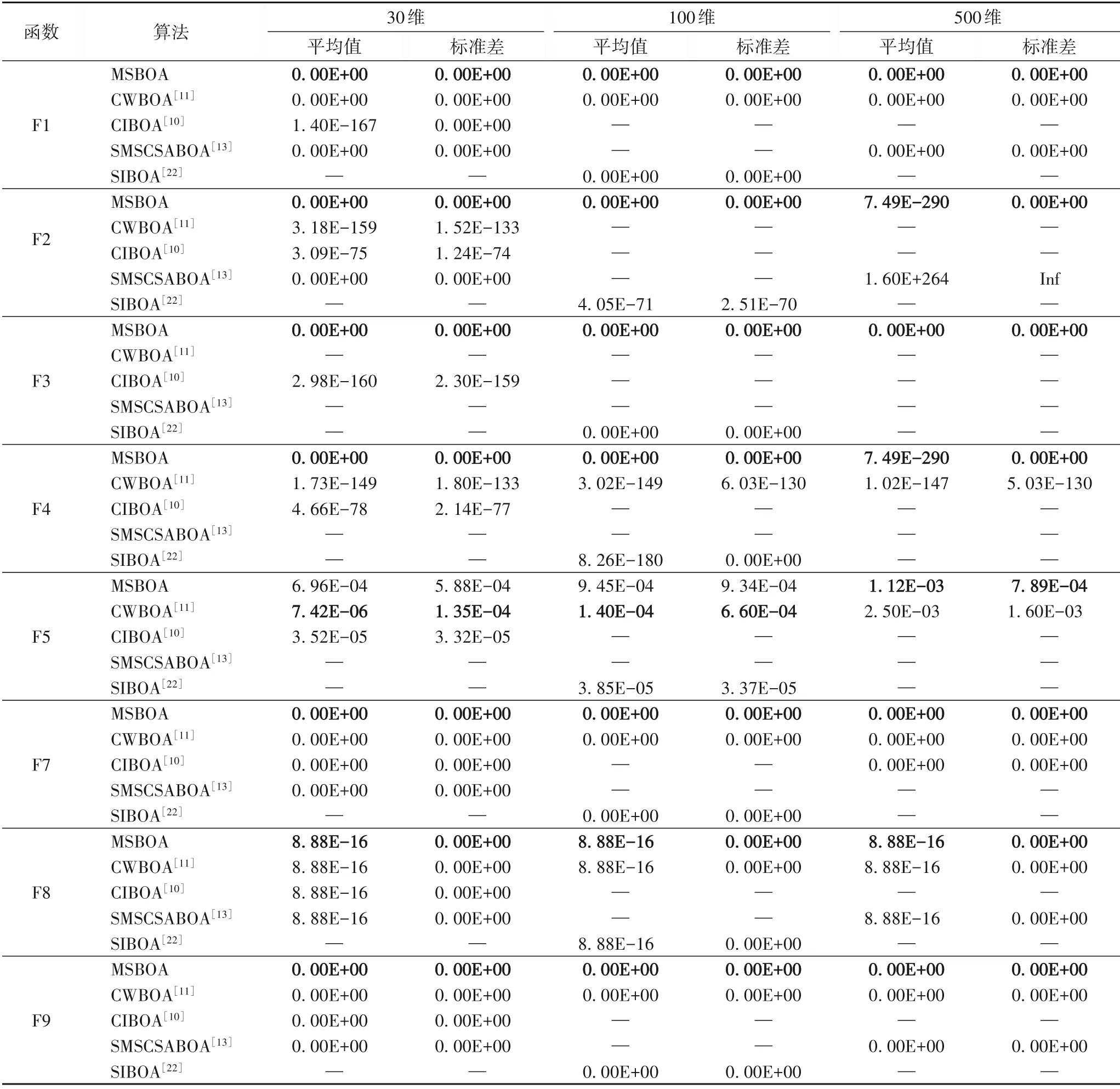
表6 不同群智能算法在不同维度下的结果比较Tab.6 Result comparison with different swarm intelligence algorithms in different dimensions

总体上CIBOA 以及CWBOA 寻优结果较差，SMSCSABOA 和SIBOA 寻优精度上相差不大，MSBOA 无论收敛精度还是稳定性上均优于其他4 种算法。具体来看，在30维度，CWBOA 在求解函数F1、F7 和F9 上能寻到理论最优值，CIBOA 在求解F7 和F9 能寻找到理论最优值，MSBOA 和SMSCSABOA 在其中给出的5 个函数上效果持平，其中MSBOA 能找到理论最优值基准函数有6个，在求解函数F5问题上，CWBOA 优于其他算法，CIBOA 次之。横向对比，在100维度上，MSBOA 保持较高的寻优精度以及稳定性，其中有6个基准函数（F1、F2、F3、F4、F7 和F9）找到理论最优值；即便在500 维度下，MSBOA 也有4 个函数（F1、F3、F7 和F9）能找到理论最优值，且在函数F2、F4 和F5 的寻优上，求解精度和稳定性优于CWBOA 和SMSCSABOA。在函数F6 上，MSBOA 的寻优精度以及稳定性与其他算法持平。综上可知，对于以上基本测试函数，MSBOA 都有较优的稳定性以及寻优能力，能有效地解决BOA求解精度不高的问题。

3.3 Wilcoxon秩和检验

在文献［23］中提出，对于改进的算法，需要进行统计检验来验证改进算法在特定问题是否与现有的算法有显著改进。为了判断MSBOA 的每次寻优结果是否在统计上与其他算法的最佳结果显著不同，Wilcoxon 秩和检验统计检验在5%的显著性水平下进行：当p值小于5%（即5.00E-02）时，“R”为“+”，即拒绝H0 假设，说明两种算法的差异性显著；否则就是接受H0 假设，说明两种算法在整体上是相同的。表7 给出了在10个基准测试函数下，MSBOA 对BOA、BOA1、BOA2、BOA3 以及樽海鞘算法（Salp Swarm Algorithm，SSA）和粒子群优化（Particle Swarm Optimization，PSO）共计6种算法的秩和检验p值。从表7 中可以观察到大部分的p值是小于5%，因此总体上说明MSBOA与其他的6种算法之间差异性显著更优。

表7 基准测试函数的Wilcoxon 秩和检验p值Tab.7 p-value for Wilcoxon rank-sum test on benchmark test functions

3.4 CEC2014基准函数上进行测试

为再次验证MSBOA的有效性和鲁棒性，在CEC2014单目标优化函数中选取部分单峰函数（Unimodal Function，UN）、多峰函数（Multimodal Function，MF）、混合函数（Hybrid Function，HF）和复合函数（Composition Function，CF）进行优化求解，对选取的部分函数总结如表8 所示，该实验在最大迭代次数上设置为1 000，算法的其他参数设置与表2保持一致。

CEC2014 函数因为具有复杂的特征，常用来验证算法的鲁棒性，将MSBOA 与BOA1、BOA2、BOA3、PSO、SSA、WOA 进行比较，部分CEC2014函数独立运行30次后取平均值的结果如表9 所示。MSBOA 在其中7 个函数上的表现优于BOA，说明本文提出的改进策略有效。其次对于CEC05、CEC12、CEC13、CEC16 测试函数，MSBOA 基本收敛到最优值的附近，表现出较强的寻优能力。对于CEC05，MSBOA 的寻优精度略低于SSA，但是MSBOA 的标准差优于SSA 和WOA，表现出较强的稳定性。对于较复杂的复合型特征函数CEC26，MSBOA同样展现出较强的寻优能力，其寻优精度仅略低于WOA。综上所述，本文提出的MSBOA 在CEC2014 函数上，同样表现出较强的寻优能力。与主流算法相比，MSBOA 的寻优精度和寻优稳定性上表现出较强的竞争能力，同时再次验证MSBOA的有效性和鲁棒性。

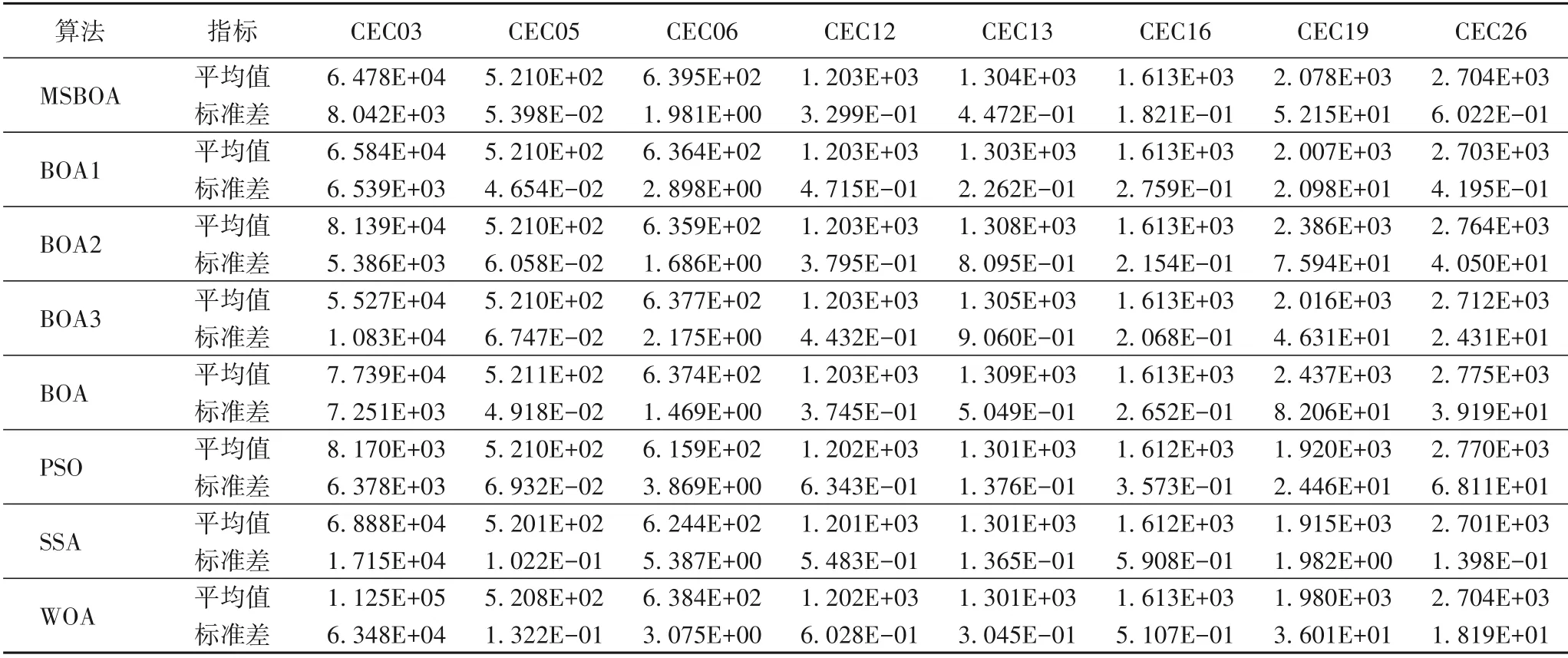
表9 CEC2014函数的优化结果比较Tab.9 Comparison of optimization results of CEC2014 functions

4 结语

为了改善BOA 容易陷入局部最优和收敛性差等问题，受余弦相似度的启发，本文提出了基于余弦相似度的位置更新策略，通过设置阈值，将相似度大的蝴蝶个体位置进行更新，并且融合旋转算子和伸缩变换算子，有效增加了全局探索能力；在此基础上，对BOA 引入了动态转换概率，更好地平衡了全局探索和局部开发；最后引入混合的自适应惯性权重，加快了BOA 收敛。四组实验显示，MSBOA 在基准的函数上求解的结果优于BOA，其次与CWBOA、CIBOA、SMSCSABOA、SIBOA 相比，MSBOA 具有很强的竞争能力。通过Wilcoxon 秩和检验，显示本文算法更优的显著性差异性；最后通过对CEC2014 部分函数的求解结果在次验证了本文提出的MSBOA 的有效性。在后续的研究中，可以考虑将MSBOA 应用到改进机器学习参数优化的问题上，进一步验证MSBOA的性能。