基于隐藏层输出矩阵的极限学习机算法优化

孙浩艺，王传美，丁义明

（武汉理工大学理学院，武汉 430070）

（*通信作者电子邮箱wchuanmei@163.com）

0 引言

极限学习机（Extreme Learning Machine，ELM）是在2004年由新加坡南洋理工大学教授黄广斌提出的一种全新单隐藏层前馈神经网（Single-hidden Layer Feedforward Neural Network，SLFN）［1］，极限学习机的网络模型分为三层，即输入层、隐藏层和输出层。输入层实现了接收外部环境的输入变量的功能；隐藏层内有激活函数主要用于实现计算、识别等功能；输出层则用于输出结果。ELM 从理论上证明了当SLFN的隐藏层激活函数无限可微时，其学习能力与输入权重和偏置等参数选取无关，即可以随机选择输入层权重和偏置［2］，无需反向调节参数。极限学习机属于一次完成型算法，能够以极快的学习速度达到较好的泛化性能，从而解决了传统神经网络学习速度缓慢的限制，拓宽了极限学习机的应用范围［3］。

ELM 算法自提出就以结构简单、学习速度快和具有良好的泛化性能著称。对ELM 算法的改进研究，主要围绕超限学习机的误差、泛化性和稳定性，包括对训练数据进行预处理，输入层权重与偏置的确定，隐藏层神经元的个数及显隐性表达，激活函数的选择等。

在数据预处理方面，对于有噪声的或丢失的数据，Man等［4］提出了对噪声数据性能的极限学习机FIR-ELM（Finite Impulse Response ELM）模型，其中输入权值是基于有限脉冲响应滤波器分配的，将隐藏层作为预处理层，增强了模型的鲁棒性。Yu 等［5］研究了缺失数据的ELM 回归问题，提出了一种Tikhonov 正则化最优剪枝极限学习机TROP-ELM（Tikhonov Regularization Optimally Pruned ELM），缺失值由传统均值替换，再采用高斯函数从输入的数据中随机选取中心，计算距离矩阵来得到隐藏层输出矩阵，从而处理缺失数据问题。

为了提高ELM 的网络结构的紧凑性，其中一种想法是以动态方式训练ELM，即在训练过程中生长、修剪或替换隐藏的神经元。Huang等［6］提出的增量ELM（Incremental ELM，I-ELM），可以从候选池中选择新添加的隐藏神经元，并且仅添加适当的神经元。Yang 等［7］提出了双向ELM（Bidirectional ELM，B-ELM）的快速增量ELM，以降低传统ELM 的网络规模。Zhang 等［8］提出了自适应ELM（Adaptive Growth ELM，AG-ELM）中，隐藏层的大小可能会在训练过程的任何步骤中增加、减少或保持不变。随后Deng 等［9］提出的两阶段ELM 算法即将ELM 和留一法（Leave-One-Out，LOO）交叉验证与逐步构建过程集成在一起，该过程可以自动确定网络的大小，并提高了由ELM构建的模型的紧凑性。

为了提高ELM 中输出权值的稳定性。Wang 等［10］证明，对于某些激活函数（如径向基函数（Radial Basis Function，RBF）），总会存在输入权重，使得映射矩阵H属于全列秩或全行秩，于是提出了一种有效的输入权重选择算法来代替ELM中的随机特征映射，从而提高了输出权重求解的稳定性。Yuan 等［11］基于H的条件以不同的方式求解输出权重：列满秩、行满秩、列和行都不是满秩的。这样与传统的ELM 相比，以更稳定的方式计算输出权重。综上对ELM 的改进，都与输出矩阵H相关，数据预处理相关的输入X、输入权重wi和偏置bi，在经过隐藏层后为H的列，神经元节点数即为H的行，输出权重的求解也与H相关，说明了挑选和改进输出矩阵H的必要性。

本文基于ELM 算法中隐藏层到输出层存在的误差，细致地分析了ELM 误差，发现误差来源于隐藏层输出矩阵求解广义逆矩阵的过程。为了进一步缩小算法误差，探寻与算法误差相关的合适目标矩阵和稳定指标，通过实验确定了目标矩阵H†H的L21 范数与ELM 的误差呈线性相关，根据此现象引入Gaussian滤波对目标矩阵进行降噪处理，使目标矩阵的L21范数改变，来达到优化ELM算法的目的。

1 相关工作

1.1 极限学习机

极限学习机是一种单隐藏层前馈神经网络（SLFN），由输入层、隐藏层和输出层组成，且由于输入权重和偏差的随机性，隐藏层到输出层为线性输出，相较于SLFN 不存在输出偏置，故极限学习机的结构如图1所示。

图1 极限学习机网络结构Fig.1 Structure of ELM network

对于N个任意不同的样本(xi，ti)∈Rn× Rm，具有L个隐藏节点和激活函数g(x)的SLFN在数学上模型为：

其中：wi=[wi1，wi2，…，win]T是连接第i个隐藏节点和输入节点的输入权值；βi=[βi1，βi2，…，βim]是连接第i个隐藏节点与输出节点的输出权值；bi为第i个隐藏节点的偏置。

当β=[β1，β2，…，βL]T，T=[t1，t2，…，tN]T和

则式（2）可以简化为：

其中：H称为神经网络的隐藏层输出矩阵。因为在ELM中，当激活函数g(x)无限可微时，输入权重wi和偏置bi可以被随机确定［1］。此时ELM的优化模型如下：

1.2 Moore-Penrose广义逆矩阵

对于任意一个m×n矩阵A，若存在n×m矩阵G满足下列Moore-Penrose方程：

则称G为A的Moore-Penrose 广义逆矩阵，记为A†。其中A*表示A的转置共轭矩阵。

1.3 矩阵的范数

矩阵的范数，是将一定的矩阵空间建立为赋范向量空间时为矩阵装备的范数。矩阵的范数能反映矩阵的某一种数值特征，故根据定义的不同，存在L1 范数、F 范数（L2 范数）、列和范数、核范数、L21范数、L12范数等［12］。

L1 范数为矩阵所有元素的绝对值之和，能够描述该矩阵的稀疏性，定义为：

F 范数（L2 范数）为矩阵的欧氏范数，即矩阵所有元素的平方和的算术平方根，定义为：

列和范数（1-范数）是将矩阵每列取绝对值求和，然后选出数值最大的那个值，定义为：

核范数是矩阵奇异值的和，定义为：

L21 范数定义为，对于矩阵W，先求每一行向量的2-范数（即每个元素的平方和再开平方根），再对生成的列向量求其1-范数（即各元素的绝对值之和），故公式为：

L12 范数同L21 范数的思想，对于矩阵W，先求每一列向量的1-范数，再对生成的行向量求其2-范数，故公式为：

1.4 Gaussian滤波

Gaussian 滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。Gaussian 滤波就是对数据矩阵整体进行加权平均的过程，每一个元素，都由其本身和邻域内的其他元素值经过加权平均后得到［13］下面的二维高斯分布：

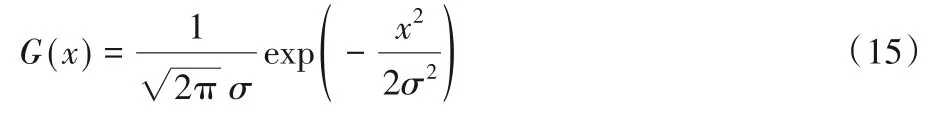
2 基于隐藏层输出矩阵的ELM优化

2.1 算法优化流程

ELM 算法流程是训练集输入为X和输出为T时，在激活函数g(x)无限可微的前提下，可随机地确定输入权重w和偏置b，产生相对应的隐藏层输出矩阵H，经过输出权重β得到对应输出值，故在训练集中，每完成一次ELM 算法，就会产生一组参数X、T、w、b、H、β和ε，且一一对应，故进行N次ELM训练后，可由误差这一指标得到N次实验中最优的一组ELM参数。

在分析ELM 算法误差ε时，发现式（4）可以进一步简化为：

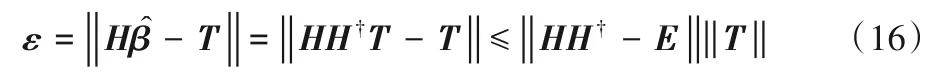
其中：E为单位矩阵。由式（16）知ELM 算法的误差来源于输出矩阵H及广义逆矩阵Η†，而且在ELM中训练集的大小远大于隐藏层神经元节点数，故H为奇异矩阵，只存在广义逆。故推断ELM 算法的误差来源于生成隐藏层输出矩阵的广义逆矩阵Η†的过程。式（16）也表明在同一个训练集时，误差即为矩阵H†H到单位矩阵的距离。根据此距离的大小可挑选出对应训练误差小的输出矩阵H，需要一个指标来衡量矩阵H†H到单位矩阵的距离，即需确定一个目标矩阵和指标来建立与ELM 误差的关系。根据此发现，设计了如图2 所示的ELM算法优化流程。

图2 ELM算法优化流程Fig.2 Optimization flowchart of ELM algorithm

2.2 算法步骤

基于ELM算法的优化流程，设计实验步骤如下：

步骤1 分析误差与输出矩阵H的关系。如式（16）所示，ε误差和辅助矩阵H†H与单位矩阵的距离大小相关。

步骤2 探寻合适的目标矩阵。在观察辅助矩阵H†H到单位矩阵的距离时，由Moore-Penrose 广义逆矩阵的定义［13］得H†H=H†HH†H=H†HH†HH†H=…，目标矩阵可能为H†H，H†H的平方或者H†H的开方。选择和(H†H)2、(H†H)3、(H†H)5、(H†H)7共9个备选目标矩阵。

步骤3 确定稳定的指标。在观察目标矩阵到单位矩阵的距离时，即要求目标矩阵的对角线元素接近于1，其他元素接近0，故引入范数这一指标来探寻与误差的存在的关系，包括L1范数、F范数（L2范数）、列和范数、核范数、L21范数、L12范数等。

步骤4 应用Gaussian 滤波进行降噪处理。针对目标矩阵进行降噪处理，因目标矩阵的指标与算法误差存在相关性，故通过改进目标矩阵的方式来降低算法误差。

3 实验与结果分析

3.1 实验环境

实验平台为Intel i7-8550U 1.8 GHz，16 GB 内存和1 TB 硬盘的笔记本，实验在Windows 10 系统上用Matlab2017（b）实现［14］。

3.2 实验设计与结果

基于隐藏层输出矩阵的ELM 算法优化旨在展现算法运算过程中所发现的隐藏层输出矩阵生成其广义逆矩阵H†的过程，拟通过实验确定目标矩阵和稳定指标与误差是否存在线性关系。设计如下4步实验：

实验1 分析误差与输出矩阵H的关系；

实验2 探寻合适的目标矩阵；

实验3 确定稳定的指标；

实验4 应用Gaussian滤波进行算法优化。

本文的训练集为服从均匀分布下随机产生500 组数据，包括输入X、输入噪声σ、输出T，如表1所示。

表1 训练集生成Tab.1 Training set generation

因ELM 在激活函数g(x)无限可微的前提下，可随机地确定输入权重w和偏置b，产生相对应的隐藏层输出矩阵H。故其中激活函数g(x)的选择也是算法重要的一步，常用的有如表2所示的三种激活函数［1］。

表2 激活函数列表Tab.2 List of activation functions

3.2.1 分析误差的来源及结果

ELM 误差存在于隐藏层到输出层的过程，其中由输出矩阵H与输出T求输出权重时，需计算广义逆矩阵Η†，误差就此产生。引入ELM 运算过程中产生的H†H为辅助矩阵，若输出矩阵为非奇异矩阵，H-1Η=E，推测辅助矩阵应更接近单位阵，产生的ELM 算法误差较小。输出矩阵H的行和列分别对应神经元节点数和训练集大小。

设计实验如下，在确定H†H的列（训练集大小）为1×500（以表1 中第1 组为例），调节H†H的行（神经元节点数）的大小来记录对应的ELM 算法误差，选用Sin激活函数，以50次实验为一组，循环100次取均值，得到数据如表3所示。

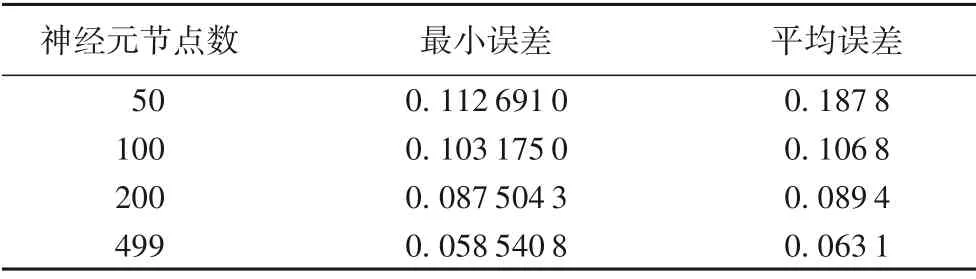
表3 神经元节点数与误差关系Tab.3 Relation between neuron node number and error

从表3 可看出，最小误差和平均误差都是随神经元节点个数的增加而减小，故输出矩阵H的变化影响着误差的变化。

进一步实验，选择最小误差对应的参数组，同时调节神经元节点数大小，观察辅助矩阵H†H到单位矩阵的距离，得到图3所示的不同节点对应的H†H矩阵数值三维图。

从图3 可看出，当节点数分别为50、100、200 和499 时，对应矩阵的对角线元素值在0.1、0.2、0.4和1.0上下浮动，相对应的误差也减小。这说明误差的大小与辅助矩阵H†H与单位矩阵的距离相关，可根据矩阵H†H到单位矩阵距离的大小来挑选训练误差小的输出矩阵H。根据实验1中发现的现象，下一步就需要引入指标来衡量矩阵H†H到单位矩阵的距离，通过实验确定与单位矩的距离更小的目标矩阵，进一步分析与误差的关系。

图3 不同节点数（50、100、200、499）对应的H†H矩阵数值三维图Fig.3 Numerical three-dimensional diagram of H†H matrix corresponding to different node numbers（50，100，200，499）

3.2.2 探寻合适的目标矩阵及结果分析

为了探寻合适的目标矩阵，由辅助矩阵H†H和Moore-Penrose 广义逆矩阵的定义，发现目标矩阵可能为H†H，和(H†H)2、(H†H)3、(H†H)5、(H†H)7等。可能的指标有L1 范数、F 范数、1 范数（列和范数）、2 范数（谱范数）和核范数等，并进行关联分析，多个目标矩阵和多个指标的关联如图4所示。

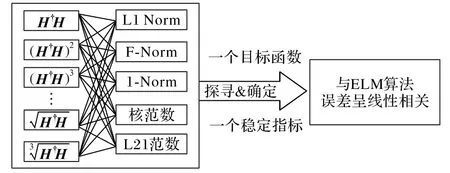
图4 多个目标矩阵与多个指标的关联图Fig.4 Correlation diagram of multiple target matrices and multiple indices

研究的对象是目标矩阵到单位矩阵的距离，暂选定能较好表示矩阵数值特征的L1范数为指标，通过实验初选目标矩阵。进行如下实验，在同一个输入X为1×500 的训练集（以表1 中组别1～4 为例），训练集生成函数为T=+e，以50次实验为一组，循环100次取均值，实验结果见表4与图5。

在表4 的12 组对比实验中，采用控制变量法来初选目标矩阵，其中自变量有训练集的噪声区间、训练集的生成函数、激活函数等，因变量为算法的误差和备选目标矩阵H†H，和(H†H)2、(H†H)3、(H†H)5、(H†H)7的L1 范数。图5 中误差与备选目标矩阵的L1 范数存在线性关系，即为后续实验确定了方向。

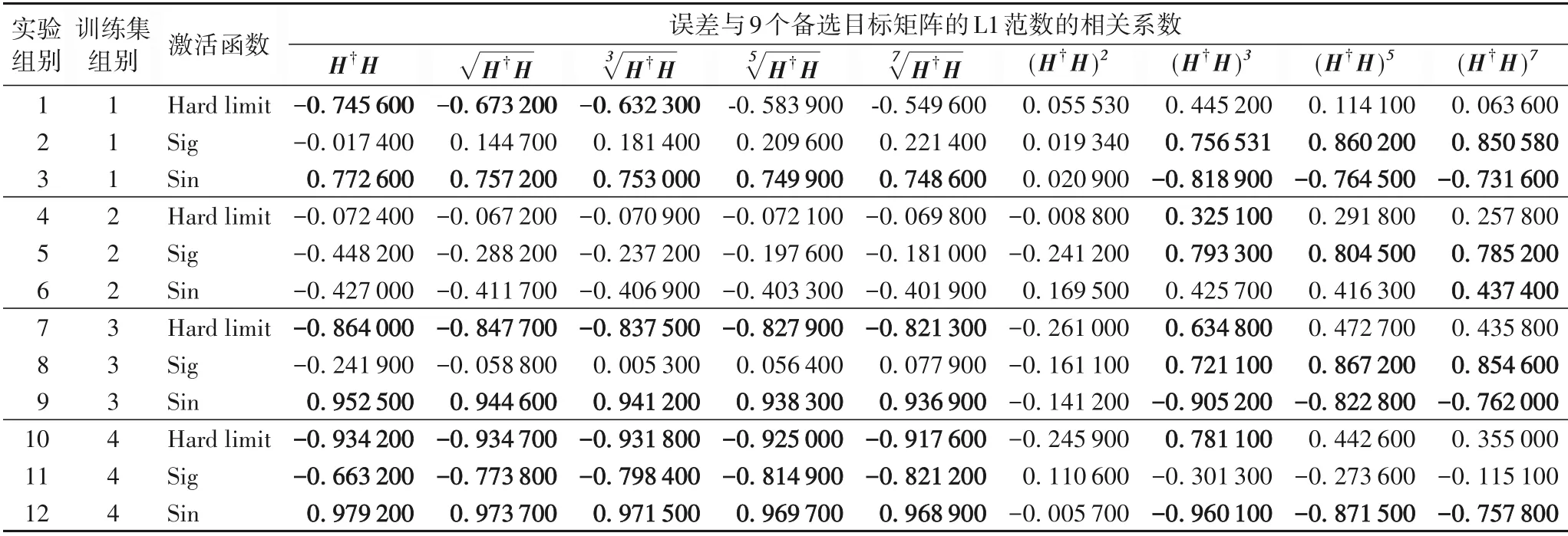
表4 误差与备选目标矩阵的L1范数的相关性分析Tab.4 Correlation analysis of error and L1-norm of alternative target matrices

图5 一次实验中备选的9个目标矩阵的L1范数与算法误差的相关性Fig.5 L1-norm of 9 alternative target matrices and algorithm error

根据相关系数的绝对值大于0.600 000 和每组实验中的相关系数绝对值最大这两个原则，计数投票出了排序前三的初选目标矩阵H†H、(H†H)3和(H†H)7，拟引入与目标矩阵相关的更多指标来进一步实验，包括L1 范数、F 范数（L2 范数）、列和范数、核范数、L21范数、L12范数这6个指标。

3.2.3 确定稳定的指标及结果分析

根据实验2 的结果，拟采用与误差的相关系数最佳的稳定指标来反向确定3 个备选目标矩阵中的最优目标矩阵，为了说明误差与目标矩阵范数指标的线性相关这一现象的稳定性，增加对比实验到48 组，表5 为3 个备选矩阵中H†H的6 种范数与算法误差的相关分析结果。

上述实验中，对3 个备选目标矩阵中H†H的6 个范数指标进行了对比实验，为了得到一个稳定的指标，对每一个目标矩阵进行48组实验并记录数据。表5中误差与L21范数的相关系数绝对值大于0.600 000 的在48 组中有29 组，大于0.800 000 的14 组。3 个备选矩阵中(H†H)3和(H†H)7同样进行48组实验，得到数据计算其6个范数指标数据（取绝对值后再平均），如表6所示。在18个指标中发现H†H的L21范数为最稳定的指标，其48 组实验的绝对数均值为0.613 300 的最佳相关系数。

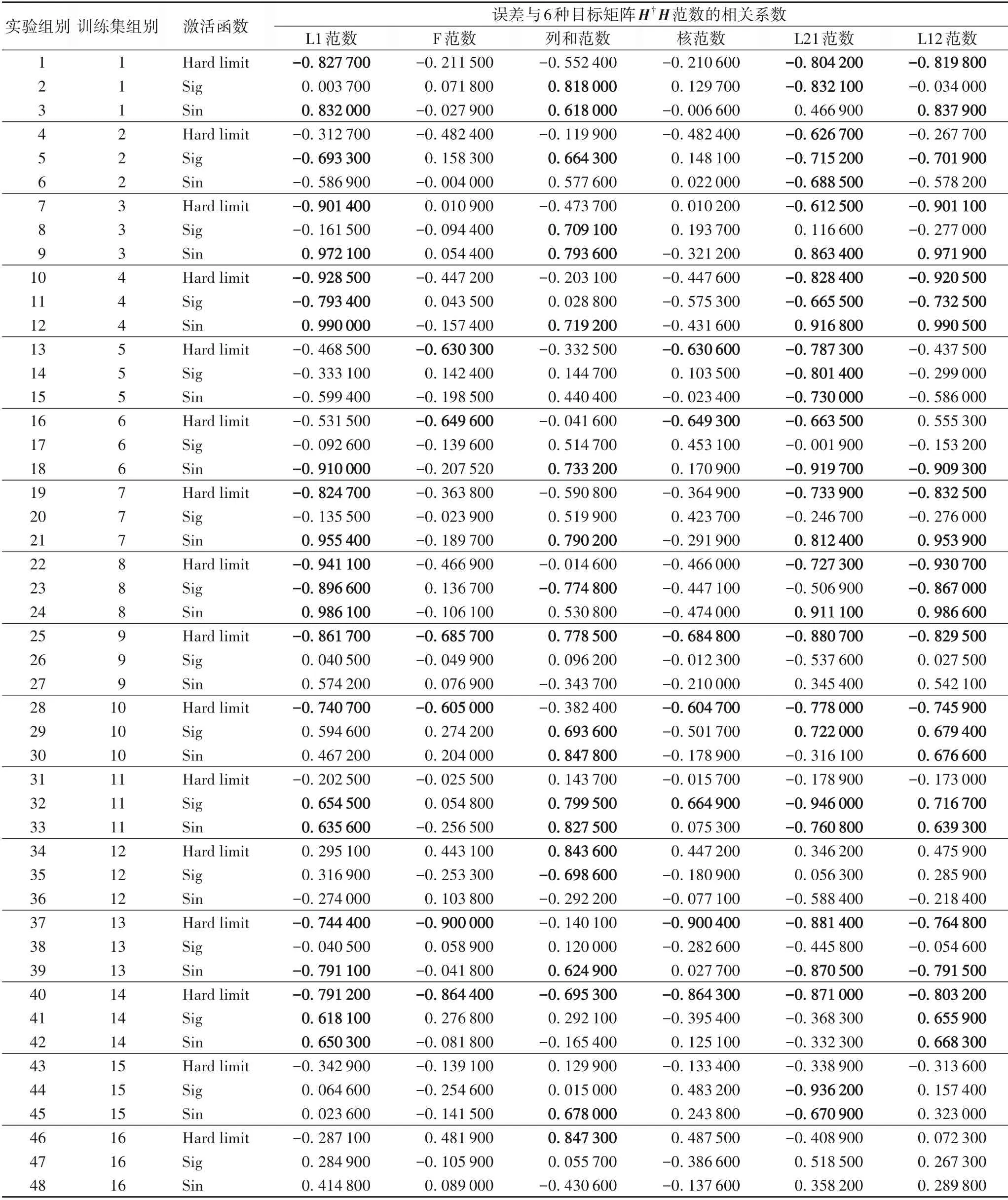
表5 目标矩阵为H†H的6个范数指标的48组对比实验数据Tab.5 Forty-eight sets of comparative experimental data for six norm indices and target matrix H†H

表6 三个备选目标矩阵与指标绝对值的均值的关系表Tab.6 Correlation table of 3 alternative target matrices and absolute average indices

3.2.4 应用Gaussian滤波进行算法优化及结果分析

确定了与ELM 算法误差呈线性相关的是目标矩阵H†H的L21范数后，根据线性相关性和矩阵范数的性质，提出采用Gaussian 滤波对目标矩阵进行降噪处理［15］，通过降低H†H的L21 范数，从而达到降低ELM 算法误差的目的。具体应用Gaussian 滤波的步骤是：①将目标矩阵H†HN×N（N为样本数）的对角线元素提出得到矩阵DN×N，再将余下的目标矩阵非对角线元素按序拉伸为行矩阵；②应用一维Gaussian 滤波优化行矩阵后，重新排列得到优化矩阵GN×N；③将优化矩阵GN×N的对角线元素替换为原对角线元素矩阵DN×N，得到优化后的目标矩阵。联系算法实验1 分析误差的来源及结果，设计如上的优化步骤，是为了在保持目标矩阵H†H的对角元素值不变，优化非对角元素值，此时降低了H†H的L21范数，达到缩小目标矩阵H†H与单位矩阵的偏差的目的。

图6 和图7 分别为目标矩阵H†H的L21 范数与算法误差呈负相关和正相关时的变化曲线，曲线表示初始数据，散点图表示滤波后的数据。图7 中正相关时，通过采用Gaussian 滤波优化了目标矩阵H†H使其L21 范数降低，从而达到了减小算法误差的目的。

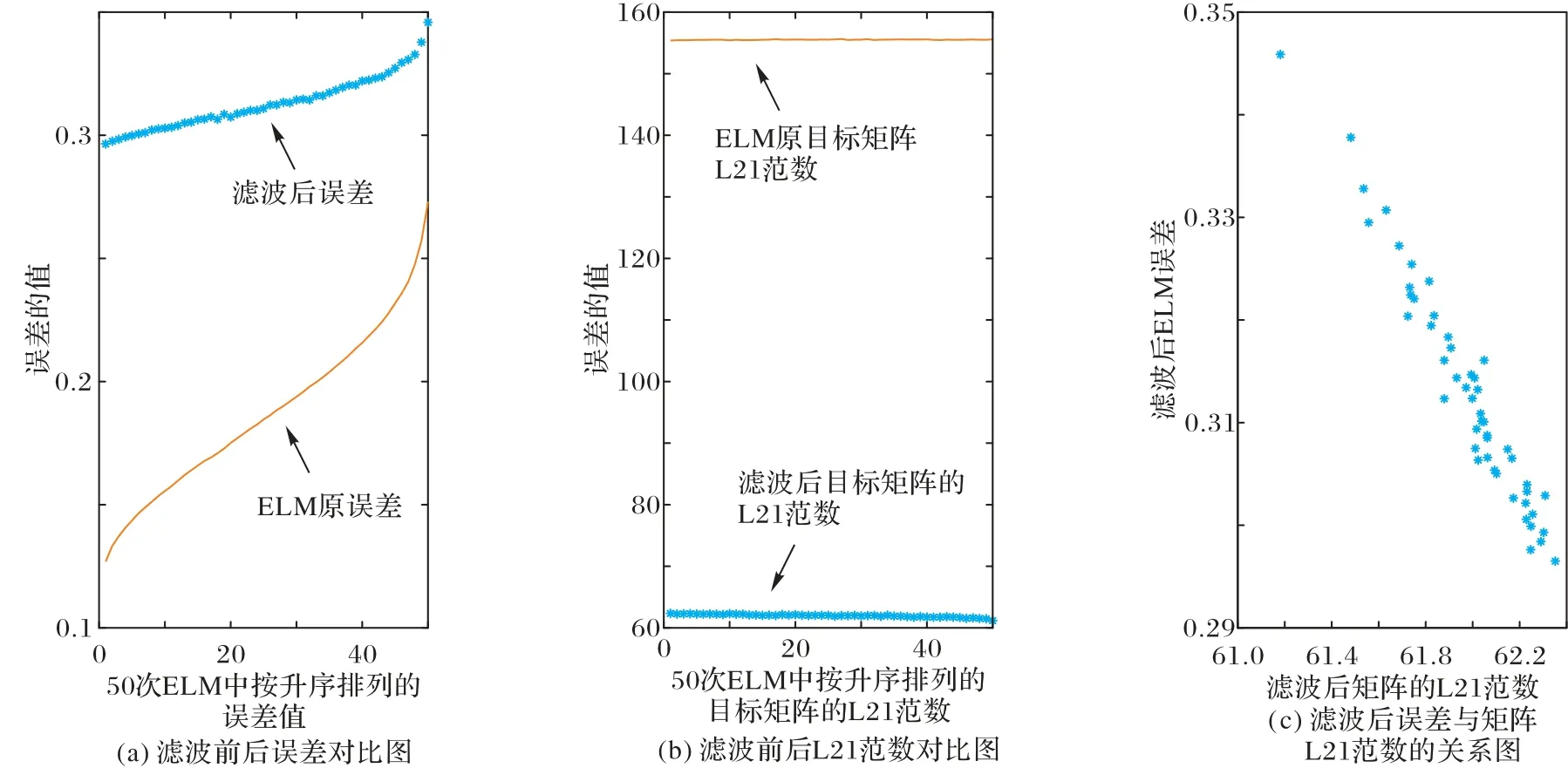
图6 滤波前后误差对比图、滤波前后L21范数对比图和滤波后误差与矩阵L21范数的关系图（负相关）Fig.6 Diagrams of error comparison before and after filtering，L21-norm comparison before and after filtering and error and matrix L21-norm correlation after filtering（negative correlation）

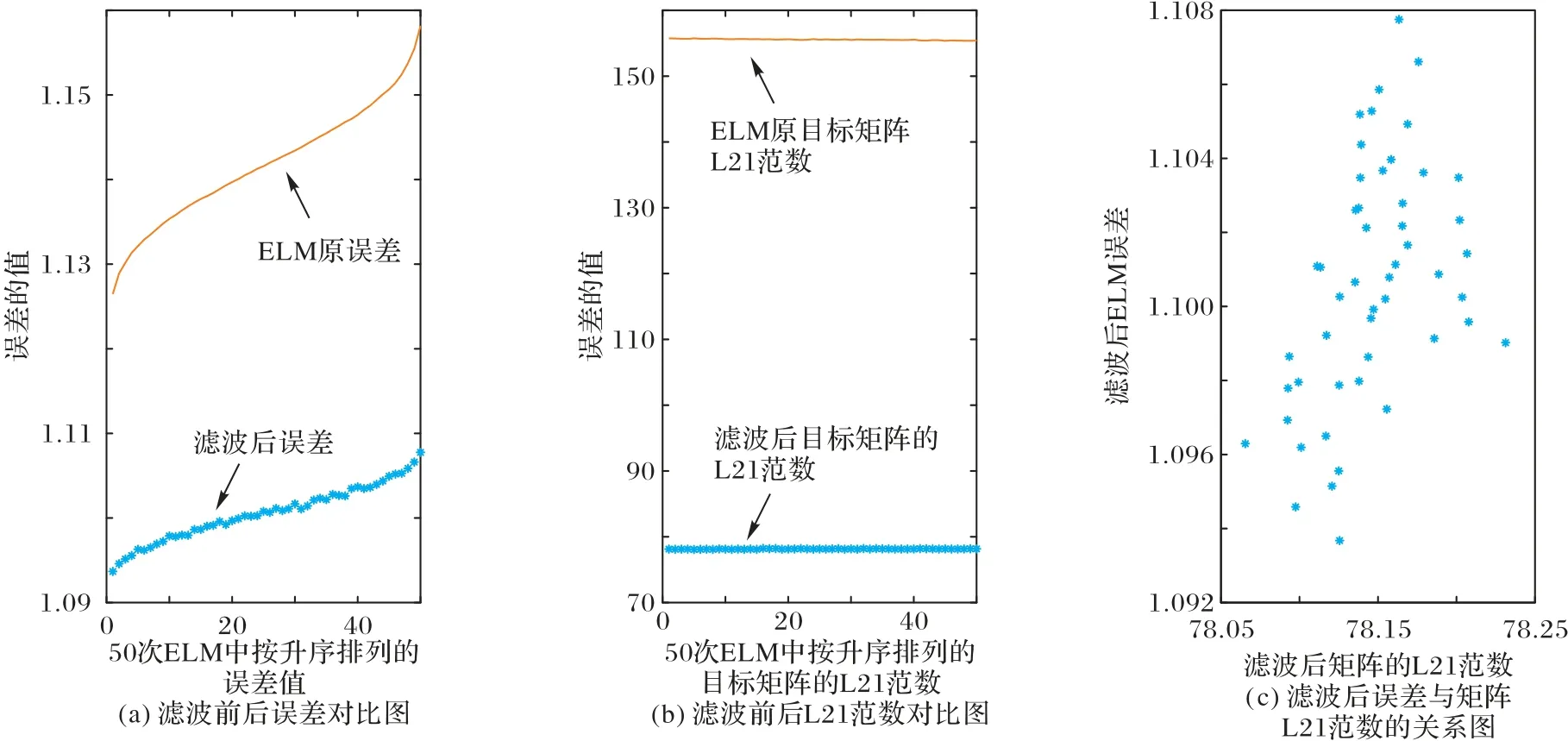
图7 滤波前后误差对比图、滤波前后L21范数对比图和滤波后误差与矩阵L21范数的关系图（正相关）Fig.7 Diagrams of error comparison before and after filtering，L21-norm comparison before and after filtering and error and matrix L21-norm correlation after filtering（positive correlation）

4 结语

本文是基于ELM 的隐藏层输出矩阵H对算法误差进行优化。在ELM 的中，训练集的大小远大于隐藏层神经元节点数，故其对应行列产生的输出矩阵H为奇异矩阵，需生成对应的Moore-Penrose 广义逆矩阵Η†来求解输出权重β，分析得出广义逆矩阵Η†的误差造成了ELM 算法的误差。根据广义逆的定义和辅助矩阵推测目标矩阵为H†H，H†H的平方或者H†H的开方和误差指标为目标矩阵的范数，设计实验得出目标矩阵H†H的L21 范数与ELM 误差呈线性相关，最后通过应用Gaussian 滤波优化目标矩阵H†H使其L21 范数改变，达到减小算法误差的目的。

ELM 作为一次完成型算法，需要多次训练后来挑选出好的输出矩阵H，每个输出矩阵H对应的训练误差都存在改进的空间［16］。实验选用了辅助矩阵H†H，在考虑优化矩阵H†H到单位矩阵的距离时，应用了Gaussian滤波对H†H进行优化，能较好地降低误差。还可以研究基于Lasso回归、演化算法等其他方法进行矩阵优化。本文研究表明对于ELM 算法，通过对目标矩阵H†H等与输出矩阵H相关的优化，或者直接对输出矩阵H的优化实验，均存在进一步降低训练误差的可能。