基于权值多样性的半监督分类算法
毛铭泽,曹芮浩,闫春钢
(同济大学电子与信息工程学院,上海 201804)
(*通信作者电子邮箱yanchungang@tongji.edu.cn)
0 引言
近年来,机器学习领域的研究十分火热,尤其是监督学习的算法研究,更是在许多的应用领域中取得了成功,但是取得完全监督的训练数据是一件很困难且耗费巨大资源的事情,因此,弱监督学习方法的研究引起了越来越多学者的关注。依据训练数据类型,弱监督学习研究[1]主要分为以下三类:不完全监督(incomplete supervision)、不明确监督(inexact supervision)和不准确监督(inaccurate supervision)三种。不完全监督是指在只有少量的标注数据、大量未标注数据的情况下进行学习,主动学习(active learning)和半监督学习(semisupervised learning)是研究中最常见的两种方案。其中主动学习[2]是指利用方法对未标注的数据打上假定正确的标签,使用标签补充完整的数据集进行模型的训练;而半监督学习[3-5]是指在学习标注数据的基础上,再利用未标注数据增强分类学习的性能。不明确监督是指数据样本仅仅具有粗粒度的标签,但没有具体样本的准确标注[6]。不准确监督是指训练数据的标注并不完全置信[7-8],其中可能存在着错误标注的样本。也就是说在这种情形下,需要在存在噪声数据的情况下学习分类模型。
相对不明确监督和不准确监督而言,不完全监督通过更好地利用未标注数据来扩充训练空间,提升学习性能。其中,半监督学习的方案是不需要人工干预的一种学习方法。半监督学习方法一共分为四类,分别为生成方法(generative method)、基于图的方法(graph-based method)、低密度分离法(low-density method)以及基于分歧的方法(disagreementbased method)。
生成方法认为标注数据和未标注数据都是来源于同一模型,其中有基于期望最大化(Expectation-Maximization,EM)算法的模型[9]、基于特征和标签混合联合概率的方法[10],以及结合EM 算法和朴素贝叶斯(Naive Bayes)的模型[11]。基于图的方法[12-14]的基本思路是对所有数据样本构建一张图,其中节点表示数据样本点,边表示数据样本点之间的某种距离度量,并设计某些标准来给未标注的数据打上伪标签(pseudolabel)。低密度分离法认为模型的分类边界应该穿过输入特征空间下的低密度区域,以此更好地区分数据样本[15-17]。基于分歧的方法是利用多个学习器对未标注样本进行分类,并在训练过程中促使不同的学习器对同一未标注样本的预测结果不同,保证分歧是训练的基础。协同训练(co-training)[18]、三体训练(tri-net)[19]是其中经典的方法,在此之外还有利用将集成学习和半监督学习结合的方法,进一步强化多个基学习器之间的分歧[20-21],利用未标注数据来增加模型的多样性,提升模型泛化性能。
相较于直接或间接对未标注数据给出标注的方法,基于分歧的半监督集成方法表现出更好的客观性与泛化性。例如基于未标注数据强化集成多样性(Unlabeled Data to Enhance Ensemble Diversity,UDEED)算法[22]利用未标注数据进行数据特征与信息的学习。而且该算法基于集成模型多样性的考虑,认为不同的基学习器应对同一未标注数据给出不同的结果,使得基学习器对于未标注数据的预测分歧不断增加。在UDEED 算法的启发下,本文提出了UDEED+——一种基于权值多样性的半监督分类算法,采用基于权值的基学习器多样性度量模块,使用未标注数据扩展基学习器的多样性。然后在损失函数中增加权值多样性损失项,在模型训练过程中进一步鼓励集成模型中基学习器的多样性,在保证模型对于标注数据学习效果的基础上,利用未标注数据扩充训练样本空间,提升模型的泛化性能。
本文的工作主要有:1)基于余弦相似度提出基学习器之间多样性分歧的度量方法;2)结合基学习器对未标注数据的预测分歧以及基学习器之间的分歧,提出一种半监督损失函数,并使用梯度下降优化该函数,进一步提升基学习器的多样性。
1 预备知识
半监督集成学习算法的基本思想是通过增大集成模型的多样性来加强模型的泛化性能。该方法的基本步骤是通过在标注数据上精确分类,学习得到一个初始算法模型,并在此基础之上利用未标注数据来增加模型的多样性,最大化分类正确率的同时,也最大化模型的多样性。
1.1 半监督集成学习问题
半监督学习问题是不完全监督研究方法中的一种,主要研究在仅有少量标注训练样本的情况下,如何利用大量的未标注数据提升模型性能。
首先,训练数据集ℵ∈Rd表示训练数据的输入特征为实数,且特征空间为d维列向量;标签Y={1,1},其中1 表示正样本,-1 表示负样本。在全集ℵ中:标注数据集合L={(xi,yi)|1 ≤i≤numL},L的大小为numL,其中xi∈ℵ,yi∈Y,未标注数据集U的 大 小 为numU,U={xi|numL+1 ≤i≤numL+numU},其中xi∈ℵ。然后,利用数据集L和U,训练一组m个基学习器{fk(x)|1 ≤k≤m},将基学习器fk(x) 的输出映射到区间[ -1,1]内,并且将(fk(xi)+1)/2 的值作为第k个基学习器将xi预测为正样本的概率值,范围在区间[0,1]内。
1.2 半监督算法基本原理
以UDEED 算法为例,该算法的训练目标在最大化分类正确率的同时,也最大化模型的多样性,这是通过优化一个全局损失函数(1)做到的:

其中:f={f1,f2,…,fm}是一组m个基学习器的集合。γ是经验损失和多样性的重要性平衡参数。D是用作增加多样性的训练数据集,有两种选项,一种是用U填充;另一种是用L+={xi|1 ≤i≤numL}填充,L+表示的是去掉标注信息,只保留输入特征信息的原始标注样本集合L,所以D=U或者是D=L+。Vemp是经验损失函数项,该项是传统的优化标注数据分类效果的一项,通过计算基学习器在标注数据集合L上的损失值,来表征当前迭代轮次的分类效果,值越小效果越好,用式(2)计算。Vdiv是多样性损失函数项,基于未标注数据集D使用式(3)计算得到。
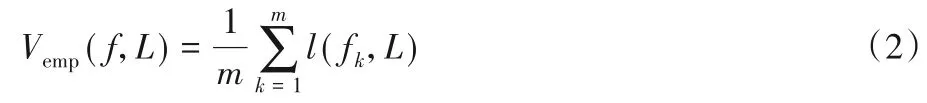
其中:l(fk,L)计算的是一个基学习器的经验损失值。

在式(3)对基学习器多样性的量化计算中,采用的是对基学习器两两配对组合的成对计算方式来衡量多样性,对于d(fp,fq,D)的计算见式(4)。
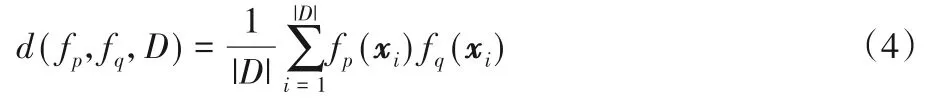
由于f(xi)的输出值是在区间[ -1,1]内的,因此如果fp和fq对xi是否为正样本的预测结果一致,那么fp(xi)fq(xi)的值是正的;相反地,如果fp和fq对xi是否为正样本的预测结果不同,那么fp(xi)fq(xi)的值是负数。
UDEED 的目的是鼓励基学习器的多样性,也就是希望产生更多不同的、更多样的m个基学习器。UDEED 认为,这种多样和不同是通过基学习器对同一样本的预测结果不同来体现的,反映到损失函数的计算上,也就是通过梯度下降优化式(3)的值,来鼓励每一对基学习器产生不同的结果。这种基于结果分歧的鼓励多样性方法,在优化计算时,没有用到任何给未标注数据打上伪标签的方法,相较于引言中提到的标注伪标签的方法,能表现出更好的客观性和可靠性;同时结合集成学习的基学习器的机制,也更能鼓励模型的多样性,以此取得更好的泛化效果。
除了以上全局损失函数的解释之外,UDEED 在优化(1)之前,先通过标注样本L初始化基学习器。对于第k个基学习器fk,使用bootstrap[23]对L采样,形成一个新的样本集合Lk={(xi,yi)|1 ≤i≤num},num为采样的样本规模,然后利用梯度下降对损失函数(5)迭代优化,其中λ是平衡模型复杂度的参数。

UDEED 的训练流程中,在扩充多样性时,先设D=L+,基于L+增加基学习器多样性;然后再设D=U,基于U增加基学习器多样性。使用这一机制的原因是为了确保标注数据的优先级大于未标注优先级,以此明确标注数据对模型训练的贡献度要大于未标注数据集。
UDEED的训练过程可以概括为三点:

1.3 半监督算法训练优化过程
针对结构化数据的半监督分类学习模型中,基学习器使用的是逻辑回归(Logistic Regression,LoR)算法,由于逻辑回归的输出值在区间[0,1]内,为了符合Vdiv多样性损失这一项定义的计算需求,需要将其输出映射到区间[ -1,1]内;同时为了简化运算,将bk放到wk中,将wk增加一个维度,变为d+1维的列向量,如式(6)所示:

接着,如式(7)所示,用BLH(fk(xi),yi)这一项表示xi的似然函数:

基学习器的初始化函数(5)的梯度为:

根据式(8)~(9)便可以计算梯度公式,并据此使用梯度下降法,迭代更新基学习器。
接着推导全局损失函数(1)的梯度,如下所示:

根据式(10)~(11)分别计算模型在D上的经验损失的梯度和多样性损失的梯度,然后据此使用梯度下降优化基学习器参数,最终得到一组基学习器f*=。
2 本文算法UDEED+
现有的半监督学习(例如UDEED)算法对于模型多样性的衡量,是基于成对的基学习器对于数据样本的预测分歧来体现的。当一对基学习器对于同一样本预测值相同时,会使多样性损失Vdiv(f,D)增大;预测值相反时,会使其减小。体现在梯度下降优化的过程中,也就是鼓励每对基学习器对于同一样本的预测不同,以体现分歧,提升多样性,本文将这种分歧称为基于数据预测导向的外分歧。基于弱分类器的集成模型,可能会导致泛化性能变弱,因此UDEED 利用未标注数据的目的是在对标注数据的训练效果影响相对较小的情况下,提升模型的泛化性能。
在此基础上,本文提出了基于权值多样性的半监督分类算法(UDEED+),并引入了余弦相似度来衡量每对基学习器的相似度,该值表示一对基学习器之间基于模型参数的内分歧,将其定义为基学习器的权值多样性(weight diversity)。通过将基于未标注数据的多样性与基于基学习器的权值多样性结合,进一步扩展基学习器的多样性,进而更好地提升模型的泛化性。在全局损失函数(1)中加入权值多样性的损失项,在迭代优化的过程中鼓励每对基学习器之间的余弦相似度越来越大,使得模型多样性进一步提升,在保证标注数据的预测效果的基础上,提升模型泛化能力和模型的预测准确性。
2.1 权值多样性度量方法
第k个基学习器的参数可以用d+1维的列向量wk表示,即如式(12)所示:
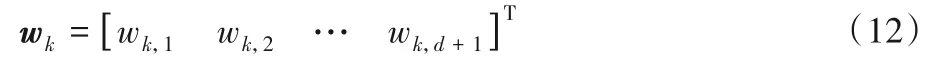
采用两个基学习器之间的余弦相似度表示一对基学习器的分歧度的原因主要是:1)计算方便;2)余弦相似度输出在区间[-1,1]内,可以表征两条向量的相似度;3)有明确的物理含义,向量夹角越大分歧度越大,两条向量越不相似。余弦相似度的计算如式(13)所示:

如果两个向量在同一空间下比较相似,那么它们的余弦相似度就会接近1;相反,如果两个向量相对不相似,那么它们的余弦相似度便会接近-1;如果从向量夹角的角度理解,当wi和wj的夹角小于90°时,cos(wi,wj)的值便为正,当wi和wj的夹角大于90°时,cos(wi,wj)的值便为负。两个夹角越大的向量,越不相似,也意味着这一对基学习器的内分歧越大,即集成的权值多样性更大。
2.2 权值多样性损失项及其优化过程
2.2.1 权值多样性损失
为了在集成学习训练过程中鼓励权值多样性,本文在损失函数中增加权值多样性损失项,如式(14)所示,成对观察m个基学习器参数向量w,计算每对基学习器的分歧度,并求和,然后再作归一化,将Vwdiv的值限制在区间[-1,1]内。

在训练时,将Vwdiv加到全局损失函数(1)中,在每次迭代更新优化时,同时计算每轮的外分歧和内分歧,确保更新参数时在经验损失项的基础上内外分歧的同步。如式(15)所示:

相对于原来的V(f,L,D),改进后的V+(f,L,D),在保证初始模型的准确率的基础上,通过加上权值多样性这一项,进一步提升了集成模型的多样性。
2.2.2 梯度下降优化推导
对于V+(f,L,D)的梯度下降优化计算,其中Vemp(f,L)和Vdiv(f,D)的计算推导可参考1.3 节的内容,不再赘述,本节主要描述V+(f,L,D)中第三项,也就是新添加的权值多样性损失Vwdiv的梯度求导过程。
首先把cos(wi,wj)展开成向量乘积的形式,这里采用的是和UDEED 中一样的成对约束,每次计算考虑一对基学习器的向量。
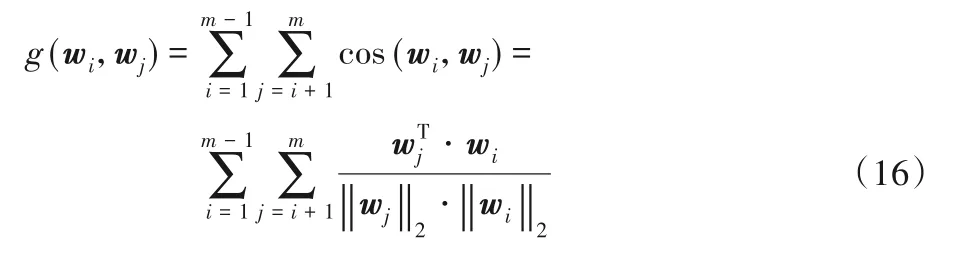
将θ视为整体的参数,θ={w1,w2,…,wm},表示m个基学习器参数向量,也就是迭代优化的对象。


将求导项展开,得到:
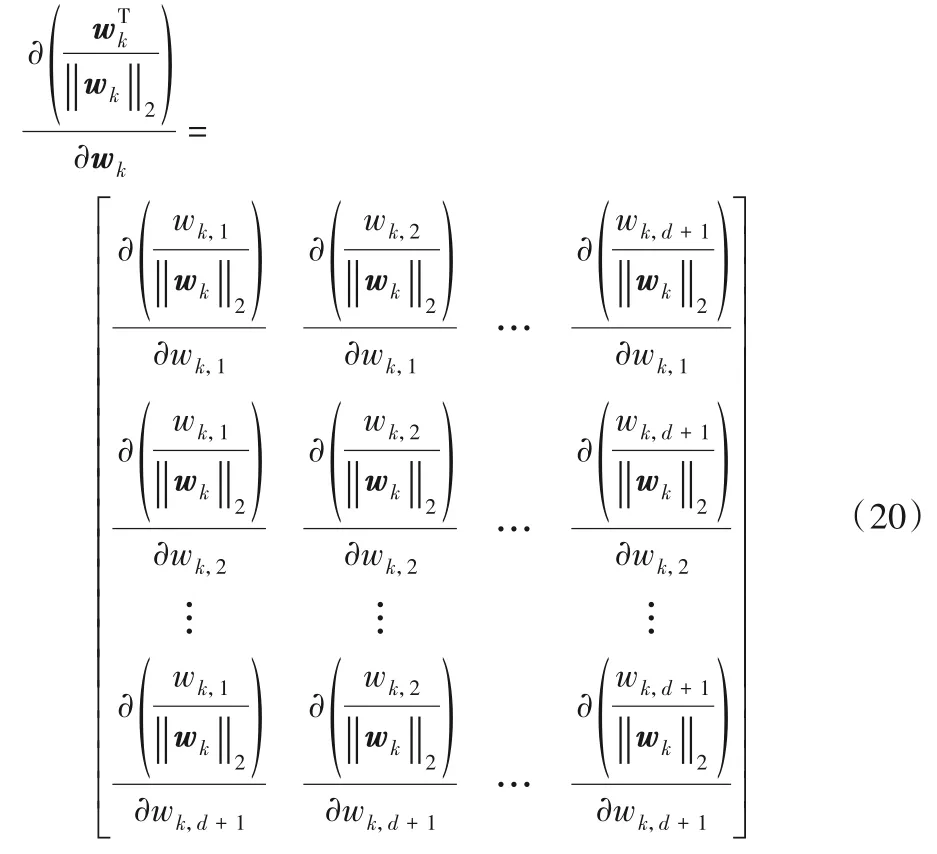
假设1 ≤p≤d+1,1 ≤q≤d+1,则式(20)的矩阵中的第p列、第q行的元素值为:

可以得到式(22)中的求导结果:

根据式(22),展开式(20)中的矩阵,可得:

对式(23)中的矩阵整理后,可得:

将式(24)代入式(18)~(19)可得最终的求导结果:

计算完所有的导数之后,接下去进行梯度下降的优化:

其中:lr是梯度下降的学习率;γ1和γ2用来平衡内外分歧对损失函数的贡献程度,本文设置γ1=γ2,以此假定两者对损失函数的贡献程度相等。
2.3 UDEED+算法流程
基于权值多样性的半监督分类算法UDEED+如下:
算法 改进的基于权值多样性的半监督算法UDEED+。


同样,本文保持了UDEED 中标注数据的贡献度高于未标注数据这一假定。
3 实验与结果分析
3.1 实验数据集描述与实验指标
本文在8 个UCI Machine Learning Repository[24]的公开数据集进行实验,数据集的介绍如表1所示。

表1 实验中使用的UCI数据集Tab.1 UCI datasets used in experiments
本节实验首先通过展现随着迭代次数的增加,损失函数的数值下降的优化过程,验证梯度下降优化新增的多样性权值损失项的可行性;接着通过图例展现随着迭代次数的增加,各个基学习器的内分歧度也随之增加,据此验证基学习器内分歧度,也就是通过余弦相似值来体现基学习器内分歧度的可行性;最后,通过在8 个公开数据集上实验结果的提升,验证UDEED+整个算法的改进效果,并以一个数据集为例展示受试者工作特征(Receiver Operating Characteristic,ROC)曲线。
为了避免不均衡数据对实验指标的影响,本实验以预测准确率和F1 分数两个指标衡量模型的性能改进。其中F1 分数的计算是正确率precision和召回率recall的调和平均值,即:

其中:TP(True Positives)表示样本真实标签为真,模型预测结果也为真的样本数;FN(False Negatives)表示样本真实标签为真,但被模型错误预测为假的样本数;FP(False Positives)表示样本真实标签为假,但被模型预测错误预测成了真的样本数;TN(True Negatives)表示样本真实标签为假,模型预测结果也为假的样本数。表2为具体的评价指标定义。
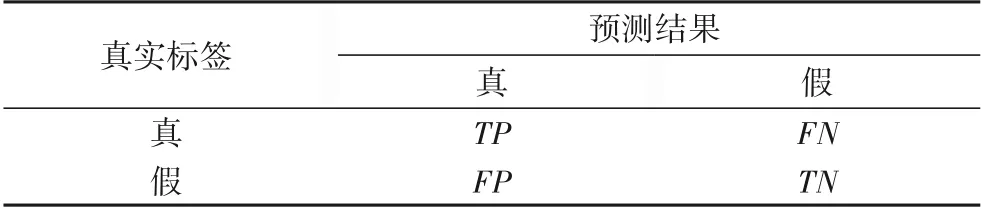
表2 评价指标定义Tab.2 Definition of evaluation indices
3.2 实验结果分析
3.2.1 损失函数的优化迭代
图1 展示的是全局损失函数、样本多样性损失项和权值多样性损失项的梯度下降过程,选取了实验中的一个数据集qsar来展示这一过程,分别对应式(15)中的V+(f,L,D)、Vdiv(f,D)、Vwdiv(f,D)这三项。从图1中可以看到,随着训练迭代次数的增加,损失函数的值随之减少,从中可以看到梯度下降的作用,需要解释的是,在迭代次数400~600,V+(f,L,D)和Vdiv(f,D)这两项的值有一个骤降,这是因为在这一步,切换了训练步骤,从第2 步的D=L+切换到了第3 步的D=U训练,由于这两项的计算中涉及到D,因此,会在这里出现一个数值的突然变化,但是对权值多样性损失项没有影响。从前后两段,以及整体的更新情况来看,总体损失值下降的趋势是没有改变的,这也验证了本文对于多样性优化的推导。

图1 损失函数数值下降过程Fig.1 Decrease process of loss function
3.2.2 基学习器内分歧
图2 展示的是基学习器权值之间的相似度的热点图(截取10 个基学习器以展示这一过程),同样选取数据集qsar 来展示这一热点图的变化过程,其中每张子图的横纵坐标分别表示的是第i个基学习器和第j个基学习器之间的余弦相似度cos(wi,wj),也就是分歧度,相似度越数值越小,分歧度越大,图中的颜色越深。图2 中的每张子图从左到右、从上到下分别表示迭代次数为0、100、200、300 时的相似度热点图。从图2 可以看出:相同位置的方块的颜色也越来越深,分歧度数值在减小,表示两个基学习器越来越不相似方块的颜色也越来越深。从整体上看,热点图的趋势体现整体基学习器的分歧越来越大,这也验证了本文对于基学习器内分歧的考量,体现了在梯度下降优化过程中,在样本多样性损失之外,结合基学习器本身的相似分歧度,进一步提高整体基学习器的多样性,增强模型泛化性能。
3.2.3 实验指标对比
实验参数设置上,基学习器个数m=20,学习率lr=0.1,其余几个影响梯度优化的参数分别设置为λ=1,γ1=1,γ2=1,此外,需要注意的是,梯度下降的停止条件设置为全局损失、样本多样性损失项和权值多样性损失项,只要有一项不再继续下降,就停止迭代,这一设置的目的主要是避免模型过度拟合,导致模型泛化性能变差。
表3 和表4 分别展示UDEED、UDEED+、S4VM(Safe Semi-Supervised Support Vector Machine)[25]、SSWL(Semi-Supervised Weak-Label)[26]四个半监督分类模型的实验结果对比。S4VM算法通过融合多个低密度分类器的预测结果来形成最终的预测模型;SSWL 在学习过程中同时考虑样本和标签相似度,以此改进模型预测性能。通过与S4VM 和SSWL 的实验结果对比,展示UDEED+算法对于未标注样本的学习效果,以此体现多样性提升对于模型预测性能的正面效果。表3 展示的是正确率指标,从整体的平均结果来看,UDEED+相较于UDEED 提升明显,提升了1.4 个百分点;对比其他模型,UDEED+也有很好的效果,正确率达到了79.2%,比第二名的SSWL 高了0.7个百分点,比S4VM高了1.3个百分点。在表4展示的F1分数衡量指标中,UDEED+比UDEED 平均提升了1.1 个百分点,仅在seismic数据集上有0.5个百分点的下降。同时对比其他模型,UDEED+的效果也很好,比SSWL 高了1.5 个百分点,比S4VM 高了3.1 个百分点,并在6 个数据集上都取得了最好的效果,平均的F1分数达到了0.656。
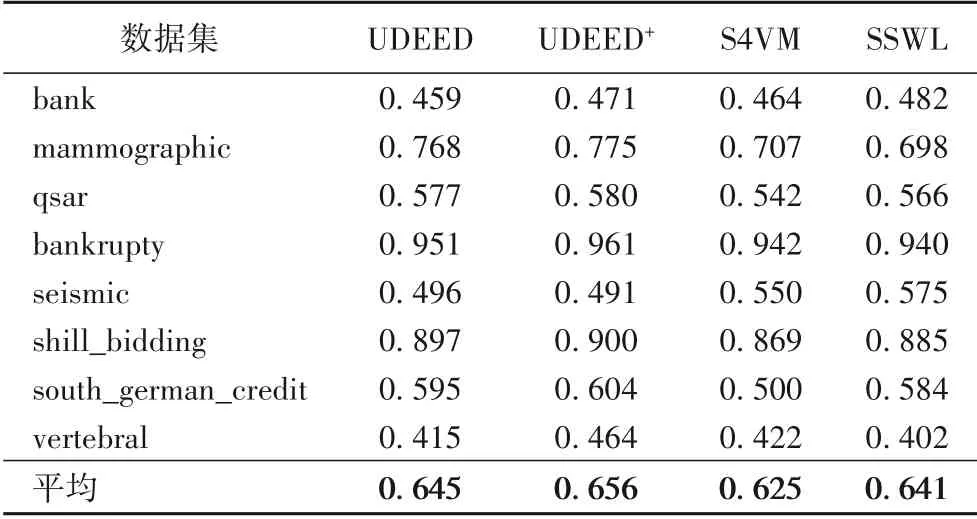
表4 UCI数据集上的F1分数对比Tab.4 Comparison of F1 score on UCI datasets
图3以qsar数据集为例,展示了UDEED、UDEED+、S4VM、SSWL 的ROC 曲线。从图3 中可以看出UDEED+算法的分类性能相对最优,ROC 曲线下的面积最大,对比其他三个算法,UDEED+算法的ROC曲线性能都有一定的改善。
综上所述,图1 中损失函数的下降过程表明了本文方法的可行性;图2 中对权值多样性可视化展示表明权值多样性损失对基学习器内分歧度有提升的作用;表3~4 中展现了UDEED+在正确率和F1 分数上的性能提升;图3 中展示了模型ROC 曲线上的改进,验证了权值多样性对于模型泛化性能的正面影响。

图3 不同算法的ROC曲线Fig.3 ROC curve of different algorithms

表3 UCI数据集上的正确率对比Tab.3 Comparison of accuracy on UCI datasets
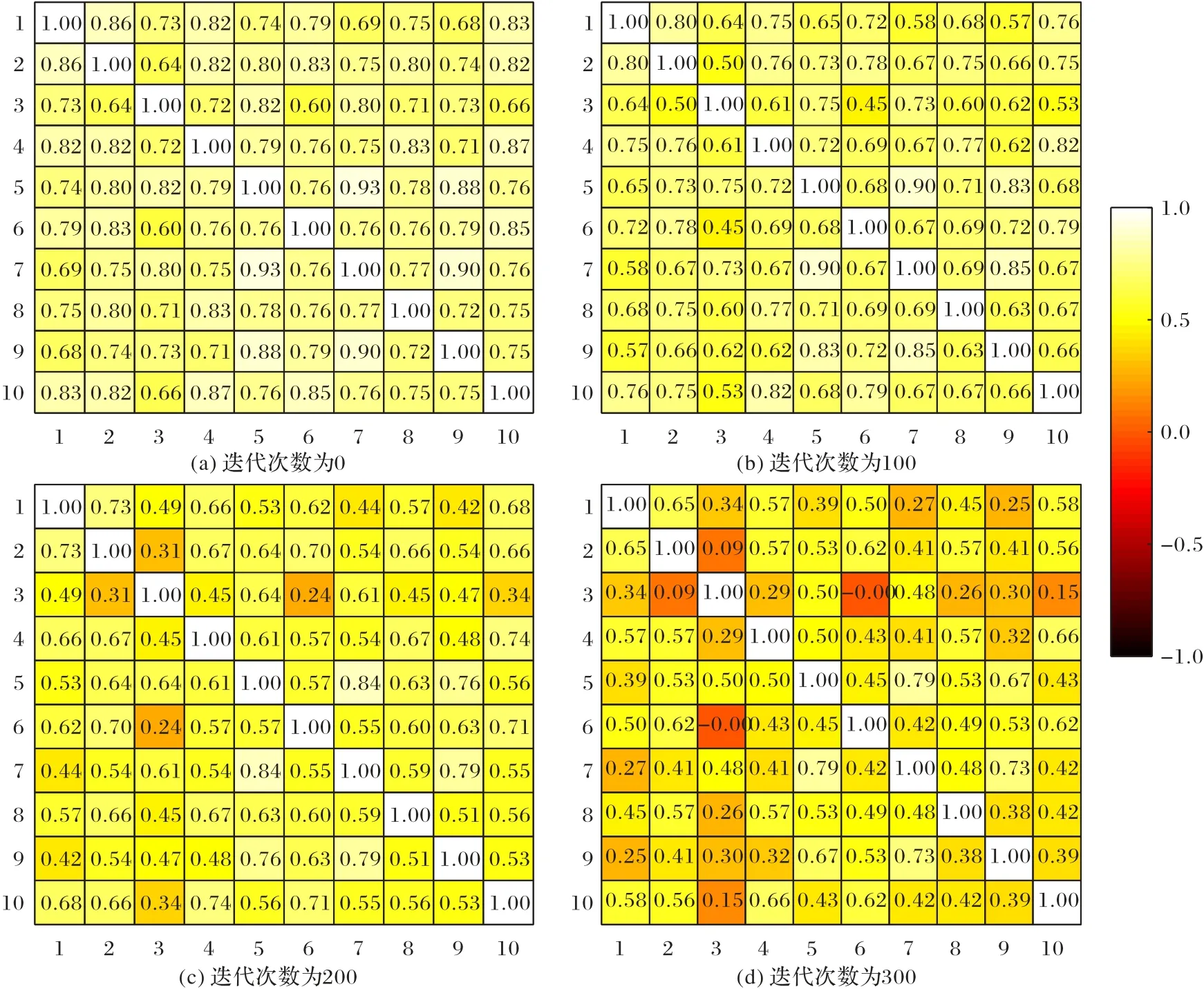
图2 基学习器权值相似度的热点图Fig.2 Heatmap of similarity of weights of base learners
4 结语
本文针对半监督学习中利用多样性提升模型性能的方法进行研究,并提出一种基于基学习器权值多样性的半监督分类算法UDEED+,该方法结合基于数据预测的外分歧和基于基学习器权值的内分歧进一步提升了基学习器的多样性,提升了算法性能。本文目前的实现主要是基于二分类问题,目前看来,之后可以根据多分类问题,探讨不同的多样性损失函数项,同时针对权值多样性和样本多样性之间的关系也可以进行进一步的探讨和研究。

