基于小斜率近似的深海海面混响*

殷丽君 吴金荣 侯倩男 马力

1) (中国科学院声学研究所, 中科院水声环境特性重点实验室, 北京 100190)

2) (中国科学院大学, 北京 100049)

收发设备在海面附近的深海混响实验中, 多途时延使得最先到达水听器的为海面混响信号, 且不受海底散射声场的干扰.本文利用射线理论描述深海声传播的格林函数, 采用粗糙界面一阶小斜率近似方法描述全角度海面散射, 给出海面混响声场的表达式.同时考虑了海面表层气泡散射的贡献, 获得了海面混响理论.通过数值仿真数据和深海实验数据的比较对海面混响模型进行验证, 分析了不同接收深度、频率下的海面混响强度衰减趋势.结果表明: 低海况条件下, 低频海面混响由粗糙界面散射主导, 气泡散射可以忽略, 随频率升高, 气泡散射对海面混响的贡献逐渐增大, 海面附近收发深度的小幅变化对混响衰减曲线的影响不明显.基于该模型提出一种反演海面粗糙界面谱参数的方法, 数值计算结果验证了该模型能够在风速已知的前提下,通过海面混响数据提取海面粗糙界面谱参数.

1 引 言

海面混响成因于海面的不平整性和波浪产生的气泡对声波的散射, 是预报低频声呐系统混响强度的重要参数之一.对海面混响开展全面研究始于二战[1], Chapman和Harris[2]首先利用爆炸声源测量低频海面混响, 总结给出海面散射强度经验公式.在这一研究之后, 开展大量低频混响测量工作[3−7], 多数情况下海面散射强度测量结果低于Chapman-Harris经验结果[8], Richter[9]推测指出这是由于测量过程中风致气泡层并未充分形成, 此外, 海面温度也是影响测量结果的原因之一.在此研究基础上, Ogden和Erskine[10,11]利用爆炸声源测量低频海面反向散射强度, 总结给出三种散射区: 对于低海况高频和所有风速条件下的低频海面, 散射特性与微扰理论描述的海面粗糙界面散射特性一致; 对于高海况下的高频海面, 散射特性与Chapman-Harris经验曲线给出的气泡层散射特性描述一致; 以及两种条件之间的临界情况.并由此将微扰散射理论和Chapman-Harris经验公式联合起来, 提出计算海面散射强度的总的散射公式.在实际的海面混响测量过程中, 由于难以满足海面充分发展、海面温度与理论符合的情况, 气泡层散射经验公式在实际使用过程中具有一定的局限性.本文通过数值计算说明, 低海况条件下的低频海面混响, 可以认为主要由水-空气间粗糙界面散射声场形成, 气泡散射作用可以忽略.

深海环境中混响信号的多途时延大于浅海, 对于声源与接收器均靠近海面的情形, 直达信号之后紧随的混响信号由海面混响主导, 不受海底散射声场的影响.关于海面混响模型的研究, Schneider[12]基于分步抛物方程给出适用于环境随水平距离变化条件下的海面混响计算方法, 其中散射核函数采用Lambert散射函数.Ellis[13]基于射线理论给出海面混响的一般表达形式, 利用Lambert散射函数描述声场散射过程, 而目前国内的有关研究相对较少.以上海面混响的测量分析以及建模计算过程中, 主要采用微扰方法或经验散射函数计算粗糙海面散射系数, 由此给出具有一定物理意义的海面混响理论.然而, 直达信号之后到达的海面混响首先是入射声与海面发生大掠射角散射, 随时间推移,掠射角逐渐减小, 而以上方法均不适用于描述全掠射角范围内散射所形成的混响声场.在海面粗糙界面散射的研究发展过程中, 常用Kirchhoff近似计算近垂向大掠射角散射, 微扰理论计算小掠射角散射[14], 假定界面斜坡足够小, 小斜率近似可以对两种散射情况给出统一描述方法[15,16].

本文利用小斜率近似方法推导格林定理描述的混响声场, 由此得到海面混响模型.通过分析南海混响实验中获取的海面混响数据, 发现低频海面混响主要来源于海面粗糙界面散射.利用实测海面混响对建立的海面混响模型进行了对比验证.最后, 利用混响数据反演获得海面粗糙界面谱参数.

2 实验数据分析

2020年在南海开展单船收发作业的深海静态混响实验.实时测量声速剖面如图1(a)所示, 由表面混合层、主跃层和深海等温层构成.海深约4370 m, 1 kg当量声弹于1000 m深度处引爆, 两个无指向性水听器分别位于其正上方距离海面31和86 m深度处.图1(b)中黑色曲线给出实验期间所测平均风速数据, 测量间隔1 min, 持续1 h, 由此得到平均风速约为4.5 m/s.

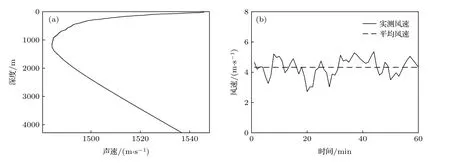
图1 实测环境数据 (a)声速剖面; (b)平均风速Fig.1.Data of experimental environment: (a) Sound speed profile; (b) average wind speed.

在1/3倍频程带宽内对实验记录的声信号数据进行滤波, 以0.05 s步长、0.1 s窗长平滑平均处理, 根据声弹源级对混响强度进行归一化处理后给出混响级曲线, 将海面反射信号到达接收位置的时刻作为零时刻.图2(a)和图2(b)分别给出声源于1000 m定深爆炸后31和86 m深度处接收到的海面混响强度随时间的变化, 中心频率为1 kHz.图中黑色虚线为十组声弹测得的原始混响数据, 蓝色实线为重复性实验平均处理后得到的混响强度衰减趋势, 将爆炸声信号到达接收点前2 s环境噪声强度的平均值作为背景环境噪声强度, 蓝色虚线为归一化处理后的环境噪声级(NL), 红色虚线标注给出混响噪声比(RNR)等于6 dB, 即混响级高于环境噪声级6 dB对应的混响级.可以发现, 重复测量得到的混响强度衰减趋势基本一致, 混响强度以相对平滑的趋势逐渐衰减, 不存在起伏包络的现象, 故认为此时体积混响对实测混响的影响可以忽略.

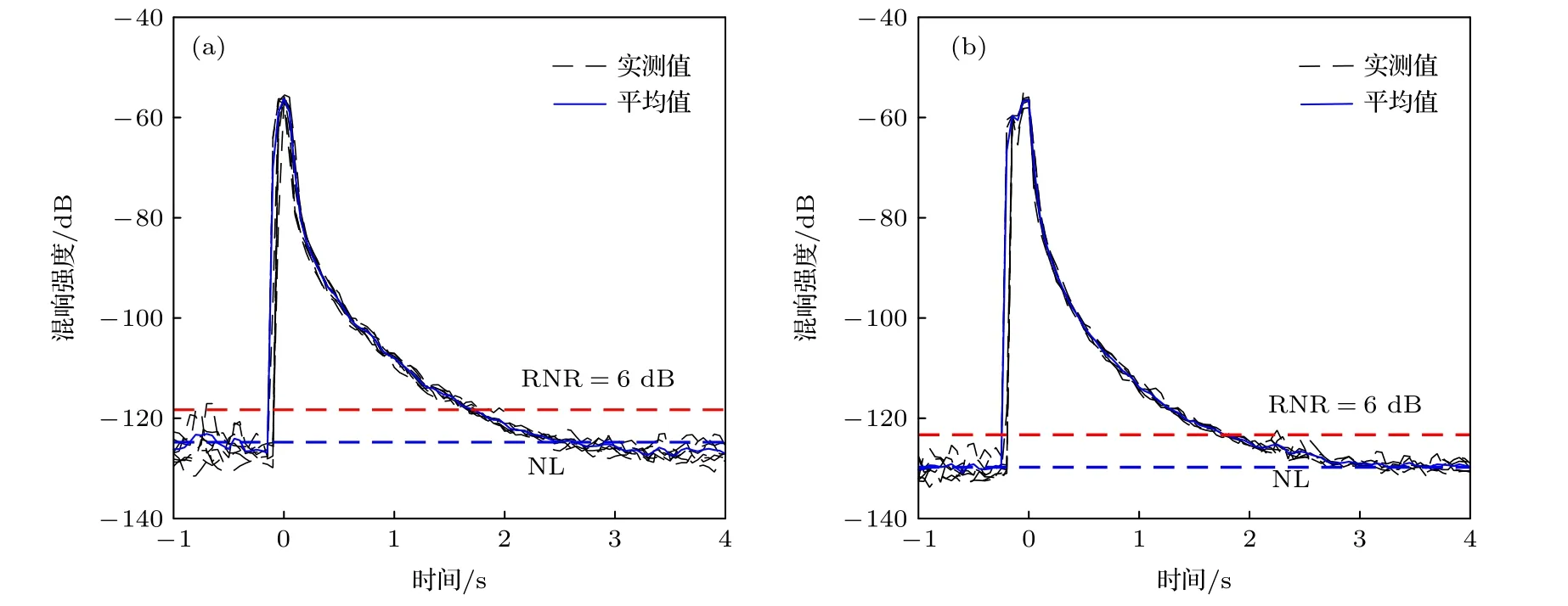
图2 实测海面混响强度衰减趋势 (a) 接收深度31 m; (b) 接收深度86 mFig.2.Decaying trend of surface reverberation intensity measured in deep water: (a) Receiving at depth of 31 m; (b) receiving at depth of 86 m.

为分析深海混响的时间结构, 这里数值仿真实验环境下无指向性声源发射声信号后, 形成海面混响、海底混响的多途声线路径.基于互易定理, 图3分别给出31和86 m深度处的出射声线轨迹示意图, 其中黑色实线代表出射角指向海底, 蓝色实线代表出射角指向海面.以海面反射信号到达水听器的时刻作为起始时刻, 由路径几何关系可知, 近垂向入射到海面并以近垂向大掠射角散射返回接收器的声线形成最早返回接收器的海面混响, 即紧随海面反射信号之后.同样以近垂向入射到海底并以近垂向大掠射角散射返回接收器的声线形成最早返回接收器的海底混响.在图3(a)中声源深度31 m、接收深度1000 m的条件下, 海底混响最早将于海面反射信号之后4.39 s到达, 在图3(b)中声源深度86 m、接收深度1000 m的条件下, 海面反射信号之后4.32 s时间内不存在海底散射声能量的干扰, 此段时间内水听器接收到的混响声信号只与海面散射有关.

图3 声线轨迹示意图 (a)声源深度31 m; (b)声源深度86 mFig.3.Geometry of ray trace: (a) Receiving at depth of 31 m; (b) receiving at depth of 86 m.

图4 (a)将图2(a)和图2(b)中两个接收深度处的平均混响强度进行比对, 可以看出, 归一化处理后31 m深度处的环境噪声级(–125.80 dB)略高于86 m深度处(–129.94 dB), 环境噪声的差异使得31 m深度处接收到的海面混响强度整体略高于86 m深度处, 而接收深度的改变对海面混响强度衰减趋势影响不明显, 两深度处接收到的海面混响大约于2.6 s开始被环境噪声淹没, 本文利用图4(a)中红色线段之间的海面混响数据进行验模及反演应用的研究.

图4(b)给出86 m深度处接收到的不同频率海面混响强度衰减曲线.图中黑色虚线代表归一化处理后中心频率1 kHz对应的环境噪声级, 可以看出, 声信号到达接收器之前, 不同频率对应的环境噪声级相近, 爆炸声信号到达接收器之后, 紧随到达的便是海面反射及海面混响, 中心频率1 kHz的海面混响强度于2.6 s开始与环境噪声接近, 随着频率升高, 海面混响强度衰减速度减慢.文献[8]指出, 声源频率为3—25 kHz对应的海面散射, 掠射角大于30°时, 海面反向散射强度与粗糙界面散射强度一致, 小掠射角范围内气泡层散射作用的影响使得海面散射强度大于粗糙界面散射强度, 对于频率低于1 kHz的情况, 实测海面散射强度数据能够与粗糙海面散射理论预报结果一致.本文第4节将对海面散射强度与频率间的这种关系进行具体的数值分析, 并由此划分本文中的高、低频段.

图4 实测混响数据比对 (a)不同接收深度间比较; (b)不同频率间比较Fig.4.Comparison of reverberation data measured in deep water: (a) Comparison between different depths; (b) comparison among different frequencies.

3 基于小斜率近似的深海海面混响理论模型

深海环境中多途时延远大于浅海, 对于近海面收发的情形, 在直达波到达接收器之后、海底反射声到达接收器之前的一段时间内, 接收器接收到的信号只包括海面反射及海面散射信号, 与海底无关.为避免海底混响的影响, 本文研究由声源直接传播到达海面的声线散射后直接返回接收器所形成的海面混响, 如图5所示, 收发水听器位于坐标系中O点所在垂线的不同深度处.这里首先考虑粗糙界面散射形成的海面混响.

图5 深海海面混响示意图Fig.5.Scenario of surface reverberation in deep water.

假设海面粗糙界面满足各向同性, 采用三维(3D)模型研究海面混响强度.单位点声源位于位置 R0=[rs,zs] , 其中 rs=(xs,ys) , 从图5可以看出,这里认为声源水平坐标为原点O, 随深度变化的水体声速为 c (z).假设声波以平面波形式入射到水-空气界面上位置 R′=[r′,η(r′)] 并发生散射, 在位置 R =[rs,z] 处接收, 单位点源在海面位置 R′处形成的声场近似满足Dirichlet边界条件 p (R′)=0.基于格林定理, 位置 R 处声场的积分方程可表示为[17]

其中 p0(R,R0) 为平坦界面条件下声源在位置 R 形成的声场, p (R′,R0) 为粗糙界面条件下声源在位置 R′形成的声场.G 为格林函数, 在声速为 c (z) 的深海环境中, 基于射线理论的格林函数表示为

其中, kw为参考点波数, 这里选取散射位置 R′为参考点, 那么波数 kw=ω/c(z′) , Asm, Ksm和 θsm分别表示第 m 条返向传播本征声线的声压幅值、波数水平分量和掠射角, 折射率 n (z)=cw(z)/cw(z′).这里只考虑最先到达接收器的声线所形成的海面混响, 即图5所示的直接由海面散射返回接收位置的声线路径, 那么只有 m =1 的情况.为简便起见,格林函数在这里可表示为

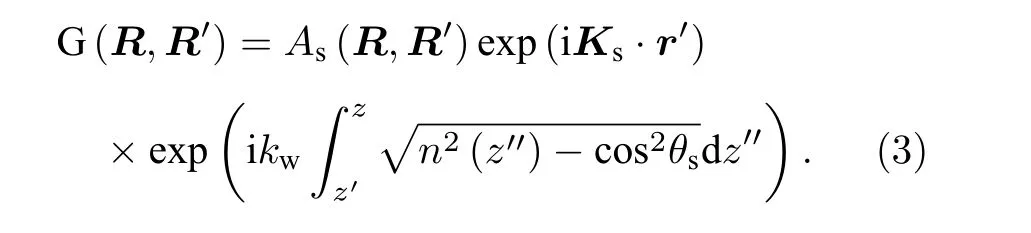
积分方程(1)中, 粗糙界面条件下形成的声场p 与平坦边界条件下形成的声场 p0之间存在关系ps=p−p0, 由此得散射声场

将(3)式代入(4)式中, 忽略边缘效应对声压幅值的影响, 则点源在水体中形成的散射声场表示为

其中,

T(k2,k1) 在物理意义上代表声源在位置 R′经粗糙界面散射后形成的声场, 下标 i,s 分别表示由声源到达散射位置的入射过程和由散射位置到达接收器的返回过程.

根据(1)式, 声压在粗糙界面位置 R′处的法向导数·∇R′p(R′,R0) 有以下关系

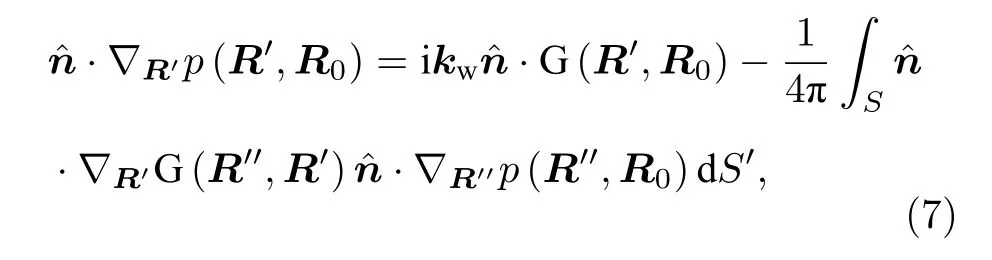
其中, p (R′,R0) 表示声场精确解, 通过迭代方法对散射声场进行求解.假设粗糙界面坡度足够小, 利用一阶小斜率近似, 文献[15]推导给出(6)式的近似表示形式

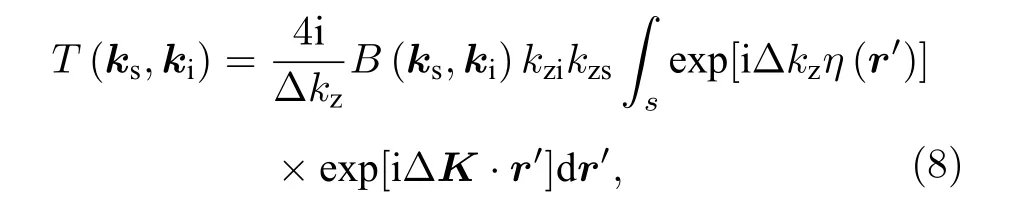
其中 kz=kwsinθs, ∆ kz=kw(sinθi+sinθs) ,∆K=Ks−Ki, 系数 B (ks,ki) 由声线的声压幅值均值确定, 由于海面粗糙界面起伏幅度远小于声源深度,根据(3)式可得:

结合(5)式, (6)式, (8)式和(9)式, 位置 R 处形成的混响声场可表示为

其中,

令散射区域中心位置距声源水平距离为 rc, 声线由声源到达散射位置并返回接收点所经历的时间为

其中

假设随机粗糙海面采用平稳统计量进行描述,对于海面起伏 η (r) 满足平稳的高斯随机过程, 且〈η(r)〉=0 , 这里 〈〉 是取均值的运算符号.为计算(14)式中的积分, 令 r′=r′′+v , 假定 v 远小于海底粗糙界面相干长度.

定义一Stochastic过程的生成函数为[17]

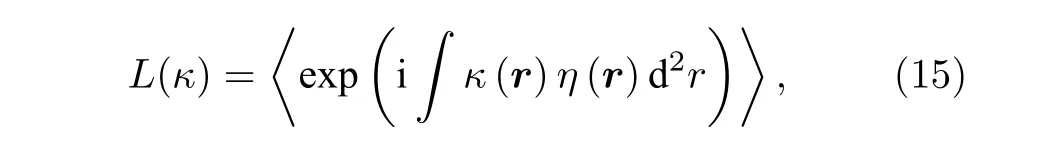
其中 κ (r) 为任意函数.当 η (r) 为均值为0的高斯函数, 生成函数有以下关系[18]

假定海面起伏近似满足平稳随机过程, 各向同性, 表示粗糙界面起伏高度的自相关函数f(v)=〈η(r′′+v)η(r′′)〉 不 随空间 发 生变化.当κ(r)=∆kz[δ(r−r′)−δ(r−r′′)], 根据(15)式和(16)式可以得到

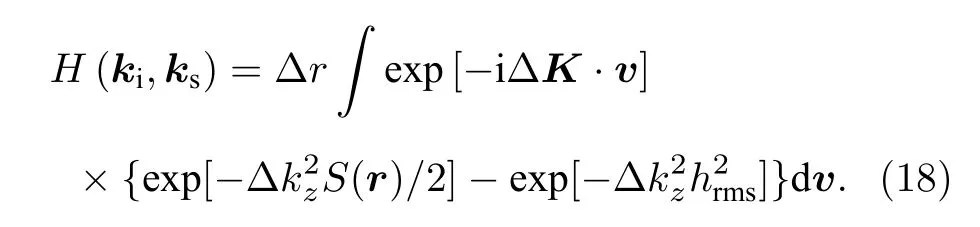
粗糙界面起伏 η (r) 的功率谱采用von Karman谱, 表示为 W (K)=w2/Kγ2[16], 其中参数 γ2称为谱指数, 参数 w2称为谱强度.对于粗糙海面,w2=QsU , U 为海面风速, 典型开阔海域中, 参数Qs∈(0.00005,0.0002) , γ2∈(3.4,4)[19], 此 时 结 构 函 数S(r)表示为[20]

假定声源脉宽为 τ0, 散射界面附近水层声速为c0, 则

将(18)式代入(13)式得

其中

物理意义上表征海面界面散射强度特性.界面粗糙特性满足各向同性时, 在极坐标下(22)式可写成[20]

对于高海况环境, 海面下风致气泡层的散射作用对海面混响产生重要影响.Gauss和Fialkowski[21]给出气泡层散射强度为

其中, kz为波数的垂向分量, d 为空气摩擦的折合深度.依据Farmer给出的海面风致气泡层散射强度经验公式, 空气摩擦的折合深度 d 与风速 U 间存在以下关系[21]:

考虑海面气泡散射后, (21)式中的散射强度项 Θ 将变成 Θ +σbub.

4 数值仿真验证

4.1 海面散射强度随频率的变化

海面混响为粗糙界面和风成气泡散射声场的叠加, 这里数值仿真海面反向散射强度与频率间关系, 其中气泡层散射利用(24)式计算.图6(a)给出不同频率下界面散射强度和气泡散射强度随掠射角的变化关系, 实线代表粗糙界面散射, 虚线代表气泡散射.为构建与混响实验相符合的海面混响模型, 根据实验期间的环境参数以及实测海面混响强度衰减趋势, 选取海面粗糙界面参数 γ2=3.9 ,QS=5×10−5m3·s.从图6(a)可以看出, 对于粗糙界面散射, 不同频率对应的散射强度相差不大,而对于气泡散射, 散射强度随着频率升高逐渐增大.图6(b)中虚线为叠加气泡散射和粗糙界面散射后得到的海面散射强度随掠射角的变化关系, 与实线给出的粗糙界面散射强度对比可以发现, 频率为1 kHz的海面散射强度和界面散射强度基本重合, 此时气泡散射作用对海面散射强度基本无影响.由于气泡散射强度与频率之间的正相关, 随着频率升高, 小掠射角范围的海面散射强度逐渐高于粗糙界面散射强度, 且两者间差值逐渐增大.本文重点分析海面粗糙界面散射形成的深海海面混响,为减小气泡层散射对海面混响强度衰减趋势的干扰, 后文工作中将选取中心频率1 kHz的混响数据进行研究.

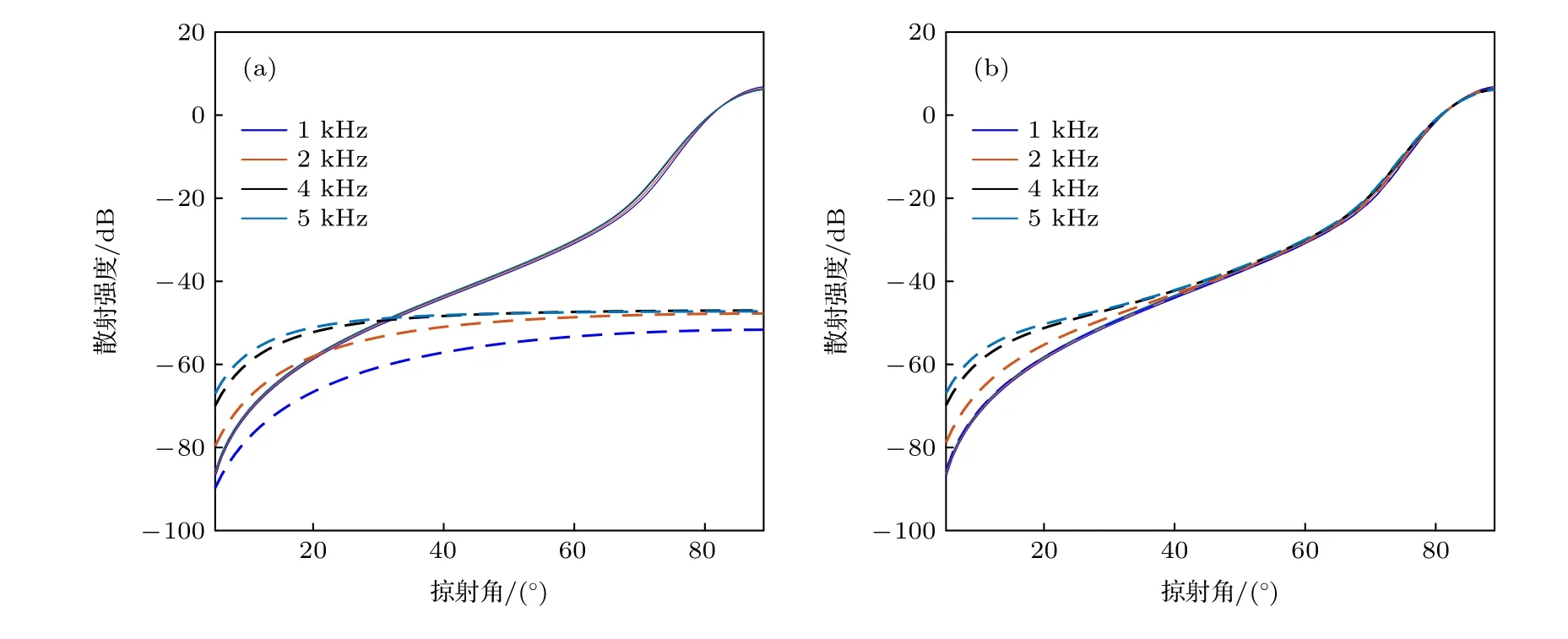
图6 不同频率下界面反向散射强度随掠射角变化关系 (a)气泡和界面散射强度; (b)界面和总散射强度Fig.6.Grazing-angle dependence of backscattering strength at different frequency: (a) Scattering strength of bubble and interface;(b) scattering strength of interface and the superposition of bubble and interface.

4.2 海面混响数值估计

图7 分别给出不考虑环境噪声、叠加环境噪声的海面混响强度数值仿真结果, 并与实测海面混响强度进行比对, 其中图7(a)接收深度31 m, 图7(b)接收深度86 m.可以看出, 叠加环境噪声的混响强度结果与实验数据整体符合较好, 说明选取的海面粗糙界面参数适用于该实验环境.对比不考虑噪声的混响强度计算结果可以看出, 图7中1 s之前的海面混响强度预报结果与实验数据符合较好, 由于海面混响强度衰减较快, 海面混响强度的数值预报结果在1 s之后与实测数据间的差异逐渐增大, 说明该时刻之后的实验数据不能直接代表海面混响强度, 因此后文将利用1 s之前的数据对该海区的海面粗糙界面散射特性进行反演.此外, 根据对图4(a)中的数据分析可以得到, 不考虑噪声影响后, 相比于86 m深度处混响数据的拟合结果,31 m深度处的数据拟合效果更差, 这是31 m深度处的环境噪声级相对更高造成的.

图7 海面混响强度拟合 (a) 接收深度31 m; (b) 接收深度86 mFig.7.Comparison between modeling simulation and measured data: (a) Receiving at depth of 31 m; (b) receiving at depth of 86 m.

4.3 海面粗糙界面谱参数的反演应用

假定实际接收到的海面混响强度为 Irece(t) , 混响参考时间为 t0, 对混响强度进行归一化处理得到相对混响强度为

这里选取海面反射信号到达接收位置的时刻作为参考时刻, 也作为海面混响衰减的起始时刻.由(19)式, (21)式和(23)式可知, 表征海面粗糙界面散射特性的参数 AS, γ2为表征相对混响强度的两个未知参数.

由于参数 QS和 γ2间不存在明确的函数关系,这里利用表征散射强度匹配程度的代价函数对两参数同时反演.选取代价函数

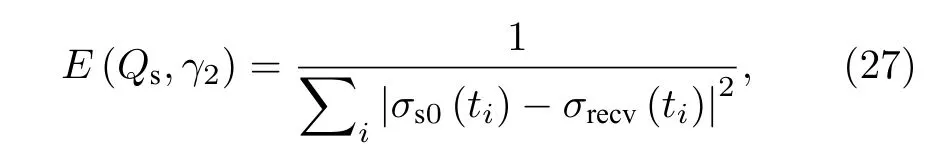
其中, σs0(ti) 为根据(21)式给出的理论模型计算得到的散射强度与时间之间的关系, σrecv(ti) 是根据实测海面混响强度得到的散射强度结果.代价函数值越大, 说明反演参数与真实参数越接近, 选最大 E 值对应的参数 Qs和 γ2作为反演结果.

考虑实测声速剖面对声线轨迹的影响, 图8给出声源于1000 m深度处发射、接收水听器分别位于31和86 m深度处接收时声线在散射位置形成的入射掠射角和散射掠射角随时间变化关系, 以进一步分析散射强度与掠射角的关系.图8中黑色曲线表示入射声线的掠射角随时间的变化, 蓝色曲线表示散射返回的声线的掠射角随时间的变化, 实线和虚线接收深度分别为31和86 m, 对比可以发现, 接收深度距离海面越近, 声线与粗糙界面间的散射掠射角减小速度越快.

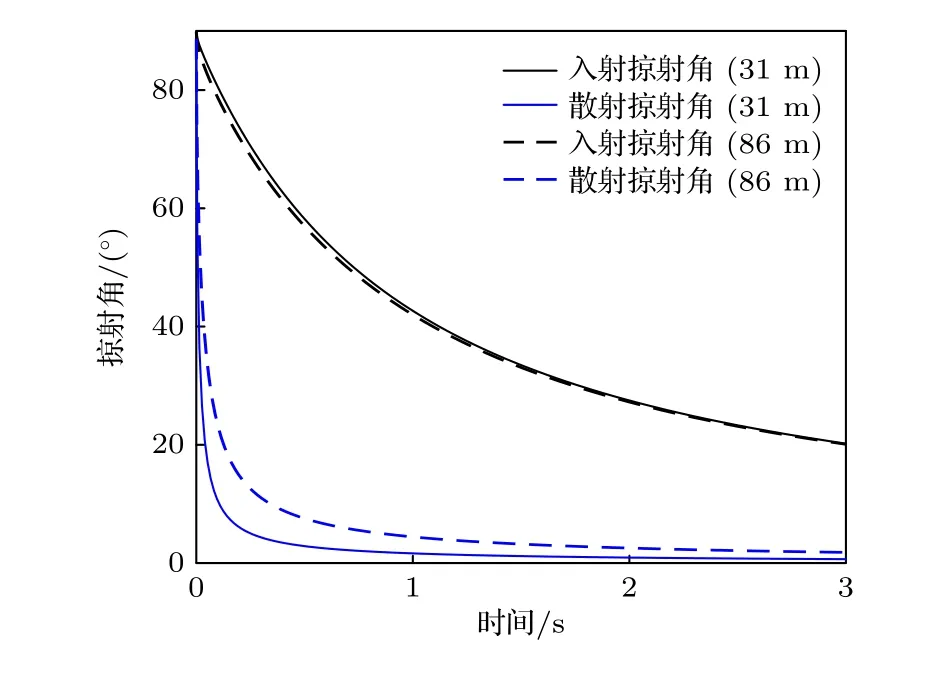
图8 掠射角随时间的变化关系Fig.8.Relationship between grazing angles and time.

利用(21)式给出的海面混响强度与海面粗糙界面散射特性间关系, 基于图4(a)中两组实测混响数据, 图9(a)和图9(b)中黑色实线为根据(22)式计算得到的海面粗糙界面散射强度随时间的变化关系, 蓝色实线为反演得到的结果, 其中图9(a)接收深度31 m, 图9(b)接收深度86 m.从图9(a)可以看出, 反演所得粗糙界面散射强度特性在0.8 s前与基于小斜率近似给出的散射模型符合较好, 随着时间的推移, 由于混响强度减小, 环境噪声影响增大, 基于实验数据得到的散射强度结果与散射模型相差逐渐增大.图9(b)中基于实测数据得到的散射强度在1.2 s之前与理论计算结果基本符合, 随后二者间差值逐渐增大.结合图8和图9可以发现, 当收发深度一致时, 入射掠射角与散射掠射角大小相同, 可以通过时间的对应关系得到海面散射强度与掠射角之间的关系.当收发深度不同时, 通过反演计算参数 Qs和 γ2可以得到海面粗糙界面散射特性.

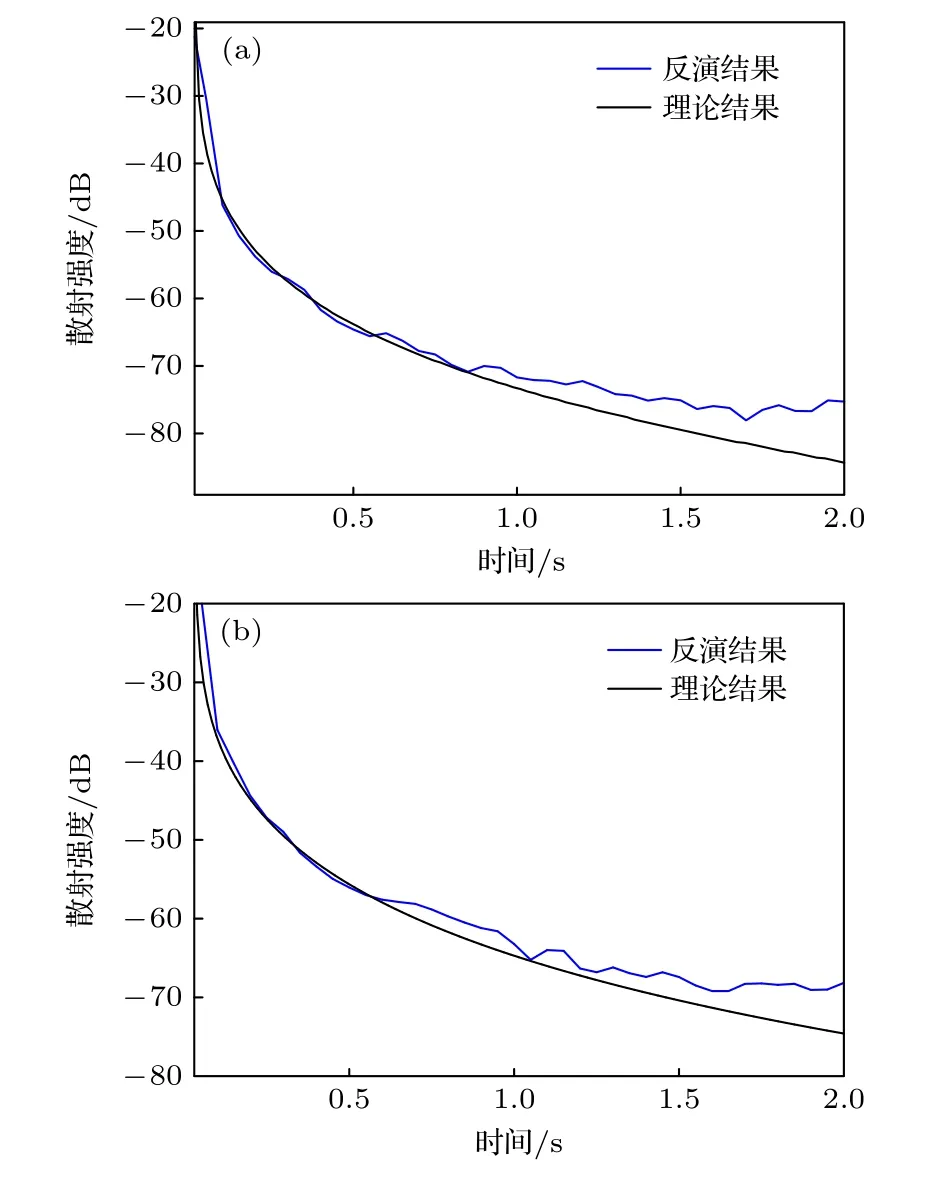
图9 海面散射强度与时间关系反演结果 (a) 接收深度31 m; (b) 接收深度86 mFig.9.Inversion results of the time dependence of surface scattering strength: (a) Receiving at depth of 31 m; (b) receiving at depth of 86 m.

根据(25)式给出的代价函数对参数 Qs和 γ2进行反演, 图10给出了归一化处理后的代价函数随海面粗糙界面谱参数的数值变化, 可以看出,代价函数最大时的参数结果为 γ2=3.9 ,Qs=5×10−5m3·s, 与海面混响拟合过程中所选取的参数符合.此外, 代价函数对谱指数 γ2相对不敏感.

图10 海面粗糙界面谱参数反演结果 (a) 接收深度31 m; (b) 接收深度86 mFig.10.Inversion results of the parameters of rough interface: (a) Receiving at depth of 31 m; (b) receiving at depth of 86 m.

5 结 论

近海面收发的深海混响实验中, 海面反射信号到达水听器之后的一段时间内接收到的混响声信号由海面混响主导.本文基于小斜率近似给出深海海面混响强度预报模型, 该模型适用于描述全掠射角范围内粗糙界面散射形成的混响声场.通过分析实测混响数据发现, 随着频率升高, 海面混响强度衰减速度减慢.数值计算结果表明, 由于气泡散射强度与频率之间呈正相关, 低频混响数据更适用于分析粗糙界面散射所形成的混响声场.本文提出的海面混响模型可以较好地预报深海海面混响.由于深海低频海面混响与粗糙界面强相关, 提出了利用深海海面混响反演海面粗糙界面谱参数Qs和γ2的方法, 通过实验数据验证了利用混响强度衰减趋势反演海面粗糙界面散射特性的可行性.该反演需输入海面风速、混响数据、水体声速、收发深度, 即可反演得到的海面粗糙界面谱参数.