快自突触反馈诱发混合簇放电的反常变化及分岔机制*

姜伊澜 陆博† 张万芹 古华光

1) (河南科技学院数学科学学院, 新乡 453003)

2) (同济大学航空航天与力学学院, 上海 200092)

簇放电是神经系统复杂的、多时间尺度的非线性现象, 具有多样性, 在兴奋性或抑制性作用下实现生理功能.近期较多研究发现了与通常概念(抑制性作用引起电活动降低、兴奋性作用引起放电增强)相反的现象, 丰富了非线性科学的内涵.本文关注于抑制性和兴奋性自突触反馈都会诱发的一类复杂的混合簇放电产生的反常现象及其分岔机制.利用快慢变量分离, 确认了放电的复杂之处: 簇结束于极限环的鞍结分岔之后要先经过去极化阻滞才到休止期.进一步, 揭示了该鞍结分岔在反常现象的产生中起到了关键作用.抑制性自反馈引起了该分岔的左移导致簇的参数范围变宽, 引起簇内峰个数增多和平均放电频率增加; 而兴奋性自突触则引起该分岔右移导致电活动降低.与其他类簇放电只在抑制性自反馈下产生反常现象和慢突触诱发的反常现象不同, 该结果给出了簇放电的反常现象的新示例及调控机制, 展示了反常现象的多样性, 有助于认识脑神经元簇放电和自反馈调控的潜在功能.

1 引 言

神经系统(脑)通过复杂非线性电活动, 如簇放电来处理信息, 进而实现感觉、认知和运动控制等功能.簇放电一般表现为快速连续多个放电峰组成的簇与休止期的交替行为, 在脑神经元中普遍存在而且模式多样, 涉及多时间尺度和复杂非线性动力学, 在兴奋性或抑制性作用特别是兴奋性和抑制性的突触或自突触调控下来实现信息处理功能[1−4].生物学实验在脑的不同部位或不同类神经元中发现了不同样式的簇放电节律模式.利用快慢变量分离, 根据簇放电涉及的快子系统的分岔以及慢变量调控下的簇放电的轨线与快子系统的分岔的关系, 在理论上将簇放电区分为多类不同的模式, 如常见的“Fold/Homoclinic”型和“Homoclinic/Homoclinic”型簇放电等[5].“/”前和后的分岔分别对应于簇的起始和结束.还有更为复杂的混合簇放电模式, 其行为除了簇和休止期, 还会有阈下振荡或去极化阻滞等[5,6], 表现出混合振荡的特征[7−9].有研究认为簇是信息处理的基本单元[10], 簇放电的模式在不同调控因素如温度、血压和离子浓度等作用下的转迁或分岔被认为与信息编码有关[11−13].特别地, 兴奋性突触调控下的簇放电增强被认为与抑郁症及药物治疗有关[1], 兴奋性自突触调控下的簇放电被认为有助于检测不同类刺激信号的时间差[14].因此, 探究不同调控因素下的神经簇放电的动力学特性对于非线性动力学和神经科学都有重要意义.

传统观念中, 兴奋性作用增强放电、抑制性作用引起放电降低, 在两者的调控下神经系统的电活动实现动态平衡, 确保生理功能的稳定[15].当兴奋性或抑制性作用过强, 则有可能引起疾病.例如,过强的兴奋性作用会引起抑郁症及对应的簇放电,药物氯胺酮会通过阻断兴奋性作用将簇放电变为单个峰放电进而缓解抑郁症[1].除了这些符合常规概念的电活动, 由于神经系统的复杂非线性特性,越来越多的反常现象被发现, 通过相位响应、分岔和慢变量对快系统的调控揭示了反常现象的动力学机制, 丰富了非线性动力学的内涵及调控神经系统功能的手段[16−21].较早被发现的反常现象是抑制性刺激引起静息变为放电的抑制后反跳(postinhibitory rebound, PIR)现象, 在众多神经系统中普遍存在, 且在信息处理和运动控制中都起到了重要作用[16,22].在生理学中, PIR现象被认为与超极化激活电流等有关[16,22]; 在动力学上, PIR现象被认为与Hopf分岔有关[5,22].此外, 在兴奋性作用之前的合适相位施加抑制性刺激, 会引起放电活动的增强, 被称为抑制后易化(post-inhibitory facilitation, PIF)现象, 在听觉神经系统的空间定位中起到了重要作用[17,23].在理论模型中, 已经发现兴奋性作用会引起网络的电活动消失[24]、抑制性耦合促进网络同步[25,26]、及抑制性自反馈作用会促进网络的信息传递能力增强的反常现象[27,28].这些进展说明进一步揭示反常现象及调控机制是全面认识神经系统的复杂动力学行为并揭示潜在生理功能的重要环节.

近年来, 自突触介导的自反馈调控吸引了越来越多的关注, 这是因为实验中发现存在自突触的神经元类型越来越多, 自突触被揭示的生理功能越来越广泛、越来越重要[29−33].例如, 抑制性自突触能引起放电降低[30]、诱发放电精确性增强[31], 兴奋性自突触引起持续性放电[32]、簇放电增强[14], 这是符合常规概念的观点.理论模型也揭示了自突触调控能够调控电活动和引起复杂的时空动力学行为[34−43].例如, 理论解释了抑制性自突触引起的放电精确性增强[39].实验研究还发现了自突触诱发的反常现象, 如抑制性自突触能够引起神经元从静息变为放电[44], 也就是PIR现象; 这一现象最近获得了理论解释[45].近期实验还发现抑制性自突触能够引起有助于维持Gamma节律的同步性而不是降低Gamma节律的同步性[46], 验证了几年前的理论模型的预期[47], 提示理论模型的结果可能会有理论先导作用.因此, 加强对自突触诱发的动力学行为特别是反常现象的理论研究, 对于扩展动力学内涵和揭示神经系统的功能都具有重要的意义.

在众多控制方法中, 负反馈常用来降低系统响应而正反馈常用来增强系统响应.而作为强非线性的神经系统, 则会出现自突触介导的负反馈引起系统放电增强而正反馈引起放电减少, 这就是反常现象.除了上述的实验发现的反常现象, 还有众多理论研究发现了反常现象.例如, 带有时滞的抑制性自突触能引起静息变为峰放电[45], 带有时滞的兴奋性自突触引起峰放电减少或放电变为静息[48].对于“Fold/Homoclinic”型簇放电, 带有时滞的抑制性自突触能引起放电增多和加周期分岔[49], 带有时滞的兴奋性自突触引起簇内峰放电个数减少但平均放电频率增加[50]; 对于“Homoclinic/Homoclinic”型簇放电, 时滞合适的兴奋性自突触引起簇内峰放电个数减少且平均放电频率减少[19].具有时滞的自突触在较大程度上等效于慢自突触.除了慢突触, 还有对于快突触的研究.对于“Fold/Homoclinic”型簇放电, 快的抑制性自突触能引起反常现象: 簇内峰放电个数增加、平均放电频率增加[18,51].进一步, 揭示了簇内峰放电个数增加是因为抑制性自突触引起簇的结束相位-Homoclinic分岔点-右移导致簇的参数区间变宽, 这就给出了反常现象的动力学机制[18]; 而快兴奋性自突触则不能引起反常现象、只能引起正常现象: 簇内放电个数增加、平均放电频率增强[51].实验和理论模型研究都已经发现簇放电是具有多类模式的[2,5], 因此, 探寻不同类型的簇放电模式在抑制性和兴奋性自突触作用下是否会出现反常现象及出现反常现象的动力学机制, 对全面认识簇放电及兴奋性和抑制性自反馈的作用、反常现象及潜在生理功能和调控作用有重要意义.

本文选取一类复杂的混合簇放电, 不同于“Fold/Homoclinic”型和“Homoclinic/Homoclinic”型簇放电, 其显著特征是在簇和休止期之间还有去极化阻滞行为[5].利用快慢变量分离, 揭示簇的起始相位对应不变环的鞍结分岔(saddle-node on invariant circle bifurcation, SNIC), 结束相位对应Fold limit cycle bifurcation(简记为FLC).在该模型中分别加入快的兴奋性和抑制性自突触[52],都能引起反常现象, 这就给出了与“Fold/Homoclinic”型簇放电的只在抑制性作用下出现反常现象不同的新结果: 合适强度的抑制性自突触电流, 可以引起簇内峰放电次数增多、平均放电频率增加; 而兴奋性自突触则引起簇内峰放电次数减少、平均放电频率减少.进一步, 通过快慢变量分离, 揭示了抑制性和兴奋性自突触引起反常现象的动力学机制:对应簇的结束相位的极限环的鞍结分岔FLC分别左移和右移引起簇的参数区间变宽和变窄.研究结果展示了簇放电的反常现象的多样性, 给出了反常现象的新示例, 揭示了调控反常现象的反馈和分岔机制, 有助于认识神经元混合簇放电的潜在功能.

2 模型与方法

2.1 改进的ML模型

在著名的二维Morris-Lecar(ML)模型的基础上, 引入反馈电流u, 形成了三维的改进ML模型,可以称为modified-ML(MML)模型[5].MML模型有三个变量, 分别为电压变量V、恢复变量w和反馈变量u, 具体模型如下:

式中 gL, gCa和 gK分别是漏离子、钙离子和钾离子的最大电导; VL, VCa和 VK分别是漏离子、钙离子和钾离子的反转电位; µ是反馈系数, 它的反转电位为 Vu; m∞(V) 和 w∞(V) 是门控变量m和w的稳态; τ是时间因子.具体表达式如下:

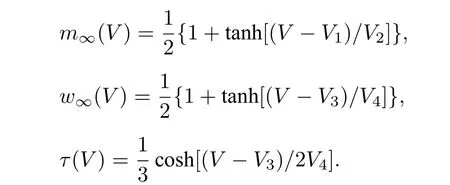
MML模型采用的参数值为 V1=−0.01 ,V2=0.15 , V3=0.1 , V4=0.16 , VL=−0.5 , VK=−0.7 ,VCa=1 , gL=0.5 , gK=2 , gCa=1.36 , µ =0.003.该模型是无量纲的.

2.2 带有自突触的MML模型

在方程(1)中引入快自突触电流 Iaut[46], 方程(2)和方程(3)不变, 得到具有自突触的MML模型, 这时方程(1)可改写成如下形式:

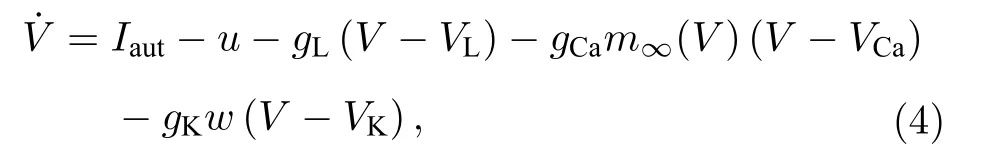
其 中, Iaut=−g(V−Vsyn)Γ(V) ,Γ(V)=1/{1+exp[−λ(V−θs)]}[46], g为自突触的电导强度,Vsyn为自突触的反转电位, θs为自突触的阈值电位,λ为神经递质的释放速率.本模型中, 自突触方程中释放速率λ的值为30; 阈值电位 θs设为–0.05,确保阈值电位低于动作电位的峰值.对于引入的自突触电流, 当研究抑制性自突触电流时, 选取自突触的反转电位 Vsyn的参数值为–0.7; 相反, 当研究兴奋性自突触电流时, Vsyn的参数值取为0.4.本文研究兴奋性和抑制性自突触的电导变化对MML模型的簇放电的影响.

2.3 快慢变量分离法

用快慢变量分离的方法来研究不同性质的自突触对MML模型电活动的影响, 探寻其中的动力学行为和机制.下面简单介绍一下快慢变量分离方法[5,19].

首先, 对方程(2)—(4)构成的带有自突触的全系统, 因为 µ =0.003≪1 , 所以选取u为慢变量, 则慢子系统为方程(3), 有自突触的快子系统由方程(4)和方程(2)组成.快子系统的表达式如下:

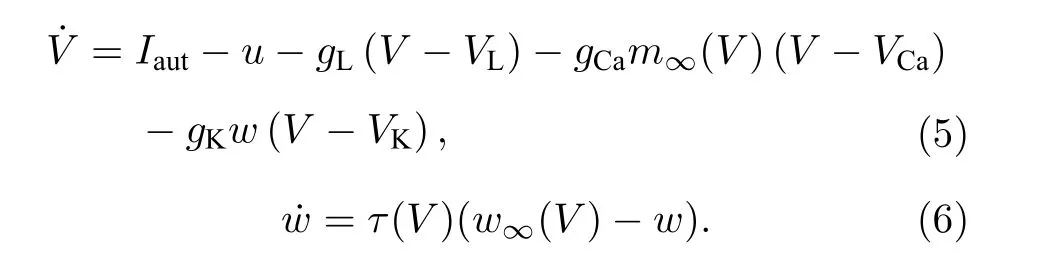
Iaut=0时方程(5)和方程(6)为无自突触的快子系统.

其次, 将u视为快子系统的分岔参数, 在(u,V)平面上得到快子系统的平衡点和极限环分岔图.

最后, 将全系统的簇放电的轨线与快子系统的分岔叠加, 探究簇的开始和结束相位与分岔关系.利用分岔来认识簇放电随电导变化的动力学行为.

2.4 计算方法

计算采用四阶龙格-库塔方法, 步长为0.005,分岔计算采用XPPAut软件[53].

3 结 果

3.1 以周期6为代表的混合簇放电

无自突触时, 改变参数 Vu的值可以得到多种复杂的混合簇放电模式.例如, 将 Vu参数值分别设为0.02, 0.05, 0.10和0.12, 膜电位的时间历程图如图1(a)—图1(d)所示, 分别对应周期3, 周期4, 周期6和周期8的混合簇放电模式.因不同混合簇放电模式在加入自突触电流后的变化规律定性一致,为避免重复, 本文取周期6的混合簇放电为代表给出研究结果.

图1(c)包括6个放电峰构成的簇, 经过短暂的衰减振荡到达高电位水平的去极化阻滞, 膜电位迅速降至低电位的休止期.簇内的第1—6个峰由数字1—6表示.而一般的非混合振荡的簇放电则没有该去极化阻滞.因此, 去极化阻滞的开始和结束或去极化阻滞本身, 在不同的调控措施下可能会具有改变簇放电动力学行为的关键作用.去极化阻滞的起始对应簇的结束.

图1 MML模型未加自突触的混合簇放电的膜电位 (a) 周期3, V u=0.02 ; (b) 周期4, V u=0.05 ; (c) 周期6, V u=0.1 , 数字1—6表示一个簇内的第1—6个峰; (d) 周期8,Vu=0.12Fig.1.Membrane potential of mixed oscillations in the MML model without autapse: (a) Period-3 bursting when V u=0.02 ;(b) Period-4 bursting when V u=0.05 ; (c) Period-6 bursting when V u=0.1 , The numbers 1–6 represent the 1st–6th spikes within a burst; (d) Period-8 bursting when V u=0.12.

3.2 周期6的混合簇放电的复杂动力学

周期6簇放电的快慢变量分离结果如图2所示.选取慢变量u作为分岔参数, 在 ( u,V) 平面上获得快子系统(5)和(6)的平衡点曲线和极限环.平衡点曲线呈“Z”型(黑色), 其上支由焦点组成,实线表示稳定焦点, 虚线表示不稳定焦点; 中支由鞍点组成, 用虚线表示; 下支由稳定结点组成, 用实线表示.在平衡点曲线的上支中, 稳定和不稳定焦点的分界点是亚临界Hopf分岔(sub-Hopf); 下支与中支交于不变环上的鞍结分岔(SNIC), 同时经过该SNIC会产生稳定极限(蓝色实线).该稳定极限和通过sub-Hopf分岔产生的不稳定极限环(蓝色虚线) 碰撞形成极限环的鞍结分岔(FLC).稳定极限环的最大值和最小值分别由 Vmax和Vmin表示.

图2 周期6簇放电的快慢变量分离 (a) 快子系统的平衡点及分岔.上支黑色实线表示稳定的焦点, 黑色虚线表示不稳定的焦点, 中支黑色虚线表示鞍点, 下支黑色实线表示稳定的结点, H点为sub-Hopf分岔点, SNIC为不变环上的鞍结分岔点.V max 和Vmin 表示稳定极限环的极大和极小值.(b) 快子系统的极限环分岔(蓝色实线表示稳定的极限环, 蓝色虚线表示不稳定的极限环)与图(a)的叠加.(c)周期6簇放电的相轨线(红)与图(b)的叠加.(d) 图(c)的局部放大, 数字1—6表示一个簇内的第1—6个峰Fig.2.Fast/slow variable dissection of the period-6 bursting: (a) Bifurcation diagram of the equilibria of the fast subsystem.Upper black solid line, upper black dotted line, middle black dotted line, and lower black solid line is composed of the stable focus, unstable focus, saddle, and stable node, respectively.H and SNIC represents the subcritical Hopf bifurcation and saddle-node bifurcation on an invariant circle.V max and V min represent the maximal and minimal value of the stable limit cycle, respectively.(b) Bifurcation diagram of the limit cycles (solid and dashed bule lines represent the stable and unstable limit cycle) of the fast subsystem and Fig.(a) plotted in one figure.(c) The trajectory of the period-6 bursting (red) superimposes Fig.(b).(d) Partial enlargement of Fig.(c).The numbers 1–6 represents the 1st–6th spikes within a burst.

图2 (c)是将周期6簇放电的相轨线(红)叠加在图2(b)中, 图2(d)是图2(c)的局部放大.图2(d)中相轨线上方数字1—6与图1的1—6相对应, 说明6个峰的相轨线为逆时针的.簇内第一个峰起始于SNIC分岔, 相轨线由下支向稳定极限环上跃迁, 受到稳定极限环的吸引, 围绕稳定极限环以大幅度的振荡开始放电, 逆时针形成6个峰后达到极限环的鞍结分岔FLC.因此, 峰结束后经上支的稳定焦点吸引形成快速衰减振荡并向右运动, 达到平衡点上支形成去极化阻滞.相轨线沿着上支向右运动穿越sub-Hopf点, 继续沿着不稳定平衡点向右运动.此时, 相轨线又受到不稳定焦点的排斥和下支稳定结点的吸引.当相轨线远离sub-Hopf点到一定程度时, 不稳定焦点的排斥和下支稳定结点的吸引足够大, 轨线从上支的不稳定焦点跃迁至下支的稳定结点上, 沿着稳定结点向左运行至SNIC形成休止期, 完成一个振荡周期.因此, 簇起始于SNIC分岔, 结束于FLC分岔, 簇结束后进入去极化阻滞.轨线由下支跃迁至上支, 上支跃迁至下支的分岔分别为SNIC和FLC, 因此该簇放电的放电模式在文献[5]中的分类为“Circle/Fold cycle”型簇放电.这里的Circle和Fold cycle分别为上文的SNIC和FLC.

3.3 抑制性自突触引起放电增强、兴奋性自突触引起放电减弱的反常现象

抑制性和兴奋性自突触作用的结果分别如图3左列和右列所示.图3左侧为加入了不同电导强度的抑制性自突触电流(红色)的膜电位(黑色)的时间历程.图3(a1), 图3(a2)和图3(a3)对应的电导分别为0.01, 0.015和0.02.随着自突触抑制性作用的增强, 簇内峰的个数明显增多, 从6增加至8,10和19.由此可见, 抑制性的自突触电流引起簇内峰的个数增加, 与传统观念的应该降低不同.

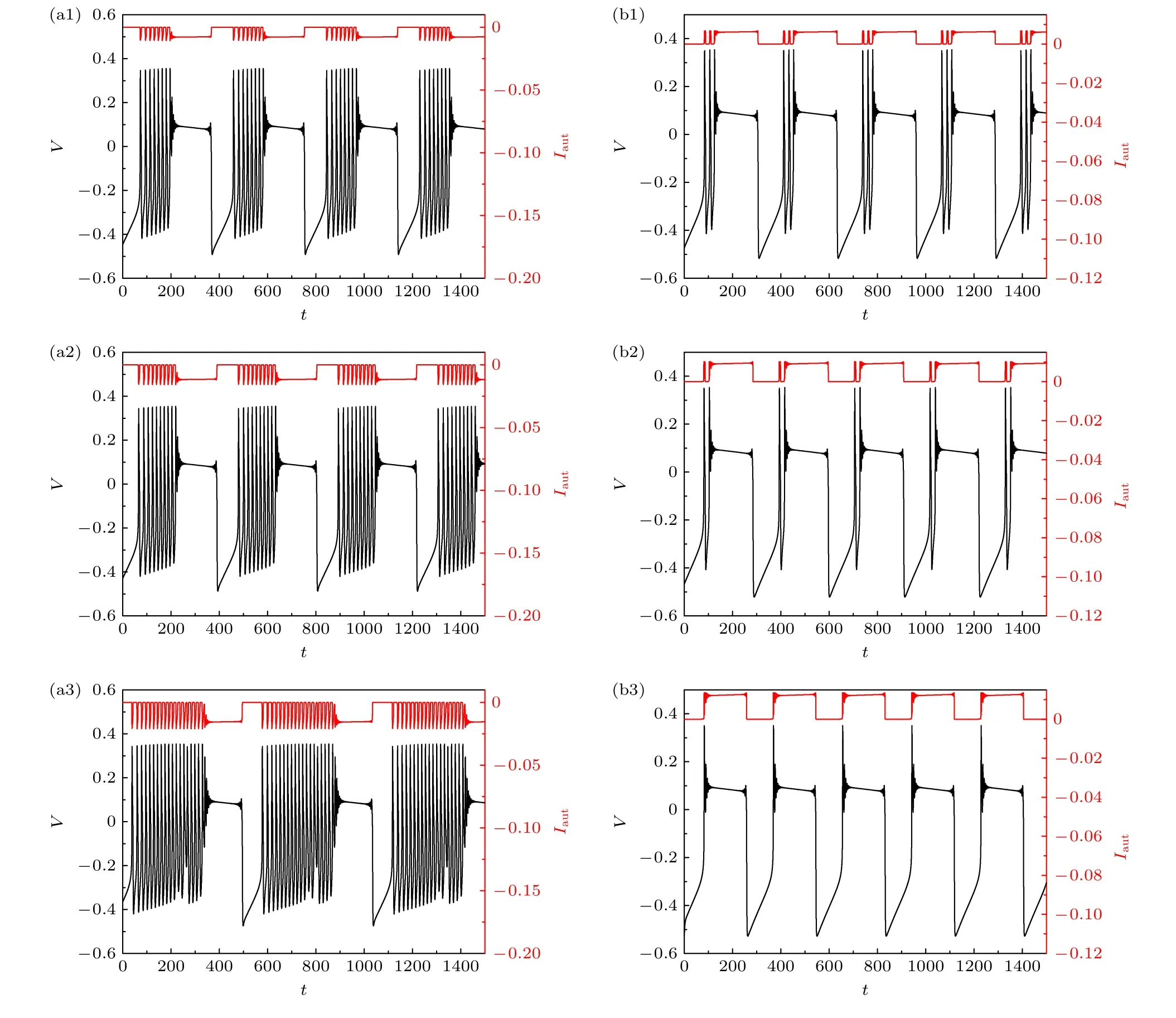
图3 自突触电流(红)影响下的膜电位(黑) (a1)—(a3) 抑制性自突触 (a1) 周期8簇放电, g =0.01 ; (a2) 周期10簇放电,g=0.015 ; (a3) 周期19簇, g =0.02.(b1)—(b3) 兴奋性自突触 (b1) 周期3簇放电, g =0.02 ; (b2) 周期2簇放电, g =0.03 ;(b3) 周期1簇放电,g=0.04Fig.3.Membrane potential (black) under the influence of autaptic current (red).(a1)–(a3) Inhibitory autapse: (a1) Period-8 bursting when g =0.01 ; (a2) period-10 bursting when g =0.015 ; (a3) period-19 bursting when g =0.02.(b1)–(b3) Excitatory autupse: (b1) Period-3 bursting when g =0.02 ; (b2) period-2 bursting when g =0.03 ; (b3) Period-1 bursting when g =0.04.

图3 右侧为加入了不同电导的兴奋性自突触电流(红色)的膜电位(黑色)的时间历程, 图3(b1),图3(b2)和图3(b3)对应的电导分别为0.02, 0.03和0.04.与抑制性自突触电流引起簇内峰个数增多的结果相反, 兴奋性自突触电流引起簇内峰的个数减少, 由6个减少为3个, 2个和1个.另外, 兴奋性自突触电流使放电呈现出明显的减弱现象, 与传统观念的应该增强不同.

抑制性和兴奋性自突触下的簇放电的峰峰间期(interspike interval, ISI)如图4(a), (b)所示.不同颜色代表不同自突触电导.图4(a), (b)给出了一个周期内的ISI随ISI序号的变化.长的ISI为两个簇的间隔, 短的ISI为簇内峰的间隔.可以看出, 不论是抑制性自突触还是兴奋性自突触,簇内峰的ISI在不同电导下差别不大, 大约为20;而长ISI, 即簇簇间隔在不同的电导下的差别也不大.因此, 对于抑制性自突触, 放电的增强主要是自突触诱发簇内放电个数增多引起的, 如图4(a)所示, 进而引起平均放电频率的增加; 对于兴奋性自突触, 放电变弱也主要是自突触诱发簇内放电个数变化减少引起的, 如图4(b)所示, 进而引起平均放电频率的降低.

图4 不同自突触电导下的簇放电的峰峰间期ISI随序号的变化 (a) 抑制性自突触, g =0 (蓝), g =0.01 (绿),g=0.015(红)和 g =0.02 (黑); (b) 兴奋性自突触, g =0 (蓝), g =0.02 (粉)和 g =0.03 (青)Fig.4.Change of ISI respect to the sequential number at different levels of autaptic conductance: (a) Inhibitory autaptic current,blue, green, red, and black lines represent g =0 , g =0.01 , g =0.015 , and g =0.02 , respectively; (b) excitatory autaptic current,blue, pink, and cyan-blue lines represents g =0 , g =0.02 , and g =0.03 , respectively.

对于抑制性自突触, 簇放电的平均放电频率随自突触电导增加而增加, 如图5(a)的上(绿)线所示, 而自突触电导的增加会引起平均自突触电流的增强, 如图5(a)的下(蓝)线所示.因此, 增强的抑制性自突触电流引起了簇放电的平均放电频率增加.对于兴奋性自突触, 随自突触电导的增加, 平均自突触电流增强, 簇放电的平均放电频率减小,分别如图5(b)的下(蓝)线和上(绿)线所示, 说明增强的兴奋性自突触电流引起了簇放电的平均放电频率降低.

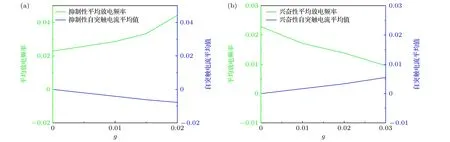
图5 平均放电频率(上, 绿)与自突触电流的平均值(下, 蓝)随自突触电导g的变化 (a) 抑制性自突触; (b) 兴奋性自突触Fig.5.Change of the mean firing frequency (green, upper) and the mean value of autaptic current (blue, lower) with respect to g:(a) Inhibitory autapse; (b) excitatory autapse.

3.4 抑制性和兴奋性自突触分别引起反常现象的动力学机制: 分岔点的变化

利用快慢变量分离的方法, 对上述不同电导强度下的快子系统的平衡点分岔以及相应的相轨线进行分析, 进一步探究反常现象的动力学机制.抑制性和兴奋性自突触对应的快子系统的分岔分别如图6左列((a1)—(a4))和图6右列((b1)—(b4))所示, 抑制性和兴奋性自突触对应的簇放电的慢变量分离的结果分别如图7和图8所示.

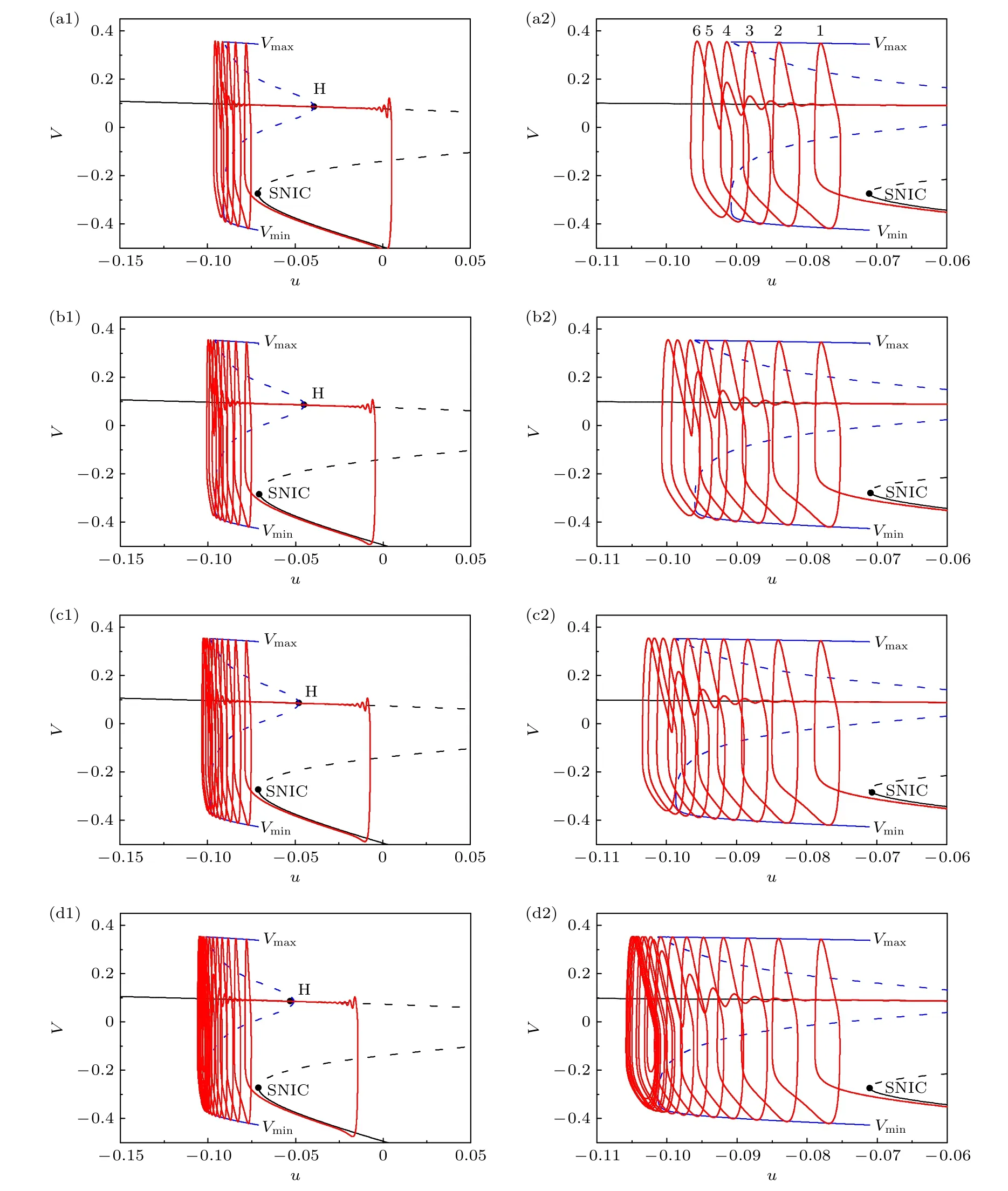
图7 不同抑制性自突触电导强度下的簇放电的快慢变量分离 (a1) g =0 ; (a2) 图(a1)的放大; (b1) g =0.01 , 数字1—6代表簇内第1—6个放电峰; (b2) 图(b1)的放大; (c1) g =0.015 ; (c2) 图(c1)的放大; (d1) g =0.02 ; (d2) 图(d1)的放大Fig.7.Fast/slow variable dissection of bursting at different values of the inhibitory autapse conductance: (a1) g =0 , and the numbers 1–6 represent the 1st–6th spikes within a burst; (a2) enlargement of Fig.(a1); (b1) g =0.01 ; (b2) enlargement of Fig.(b1);(c1) g =0.015 ; (c2) enlargement of Fig.(c1); (d1) g =0.02 ; (d2) enlargement of Fig.(d1).

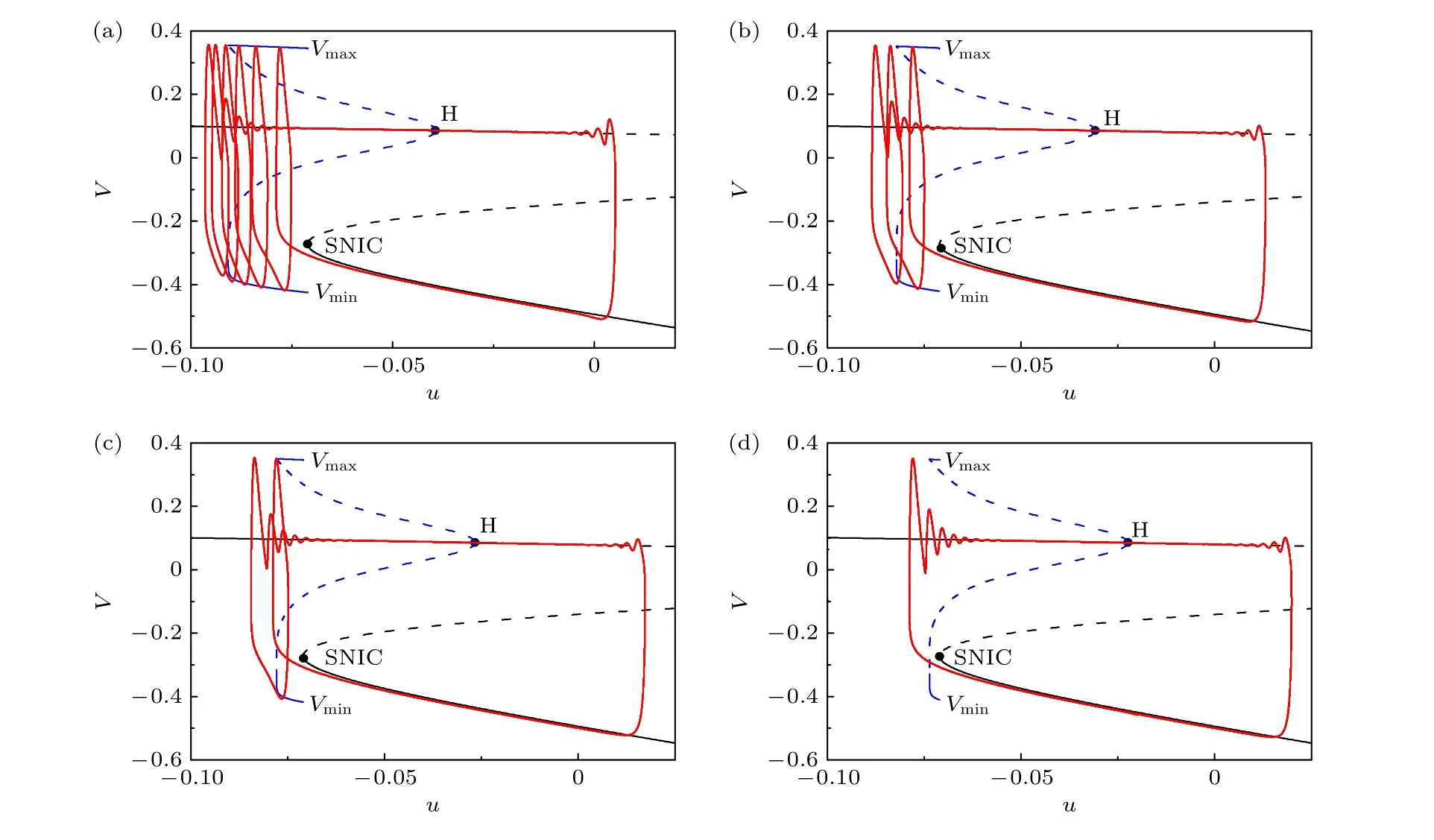
图8 不同兴奋性自突触电导强度下簇放电的快慢变量分离 (a) g =0 ; (b) g =0.02 ; (c) g =0.03 ; (d)g=0.04Fig.8.Fast/slow variable dissection of the bursting at different values of the excitatory autapse conductance: (a) g =0 ;(b) g =0.02 ; (c) g =0.03 ; (d) g =0.04.

图6(a1)给出了抑制性自突触电导强度g为0(蓝), 0.01(绿), 0.015(红)和0.02(黑)的快子系统的平衡点曲线.图6(a2)为u在(–0.08, –0.02)范围内的放大.随着抑制性自突触电导强度的增加,sub-Hopf点的u值减小, 具体表现为向左移动, 而SNIC几乎不变.而对兴奋性自突触, 随着电导强度增加, sub-Hopf点向右移动, SNIC几乎不变, 如图6(b1), (b2)所示.

图6 不同自突触电导强度下快子系统的分岔 (a1)—(a4) 抑制性自突触: (a1)平衡点分岔; (a2) 图(a1)的局部放大; (a3) 极限环分岔与图(a1)的叠加; (a4) 图(a3)的局部放大.电导强度的取值为 g =0 (蓝), g =0.01 (绿), g =0.015 (红)和 g =0.02 (黑).(b1)—(b4)兴奋性自突触: (b1) 平衡点分岔; (b2) 图(b1)的局部放大; (b3) 极限环分岔与图(b1)的叠加; (b4) 图(b3)的局部放大.电导强度的取值为 g =0 (蓝), g =0.02 (粉), g =0.03 (青)和 g =0.04 (棕)Fig.6.Bifurcations of the fast subsystem at different values of the autapse conductance.(a1)–(a4) Inhibitory autapse: (a1) Bifurcations of the equilibria; (a2) partial enlargement of Fig.(a1); (a3) bifurcations of the limit cycles superimposes Fig.(a1); (a4) partial enlargement of Fig.(a3).Blue, green, red, and black lines represent g =0 , g =0.01 , g =0.015 , and g =0.02 , respectively.(b1)–(b4) Excitatory autapse: (b1) Bifurcations of the equilibria; (b2) partial enlargement of Fig.(b1); (b3) bifurcation of the limit cycles superimposes Fig.(b1); (b4) partial enlargement of Fig.(b3).Blue, pink, cyan-blue, and brown curves represents g =0 ,g=0.02 , g =0.03 and g =0.04 , respectively.

图6 (a3)和图6(b3)中, 除了不同电导强度的快子系统的平衡点曲线, 还给出了极限环相关的FLC分岔和稳定(实线)、不稳定(虚线)极限环的最大值(上)和最小值(下).随着抑制性自突触电导强度的增加, FLC点对应的分岔参数减小, FLC点向左移动, 所以稳定极限环对应的分岔参数的区域范围变宽, 如图6(a3), (a4)所示.图6(a4)为图6(a3)的局部放大图.对于兴奋性自突触, 随着电导强度的增加, FLC点向右移动, 稳定极限环对应的分岔参数的范围变窄, 如图6(b3), (b4)所示.

在图7中, 将抑制性自突触作用下的全系统的簇放电的相轨线(红色)在 ( u,V) 平面投影叠加在快系统的分岔图(图6(a3))上, 进一步揭示分岔对簇放电的变化的影响.图7中的左列从上到下对应不同电导, 右图为左图的局部放大.施加抑制性作用的自突触电流后, 放电模式没有发生改变, 簇大约位于FLC和SNIC之间, 簇放电的时间历程与没有自突触的类似.但是, 随着电导的增加, FLC点左移, 而SNIC几乎不变, 簇的参数范围变宽,导致簇内放电个数增加, 放电增强.因此, FLC点的左移是簇内峰放电个数增加的原因.

图8为不同电导强度下兴奋性自突触对应的簇放电的快慢变量分离的结果.可以看出, 与抑制性突触的结果类似, 电导变化没有引起簇模式的变化.放电簇位于FLC和SNIC之间, 放电轨线的运行方向与无自突触的周期簇类似.与抑制性自突触结果不同的是, FLC随着电导增加右移, 引起放电簇的参数区间变窄, 导致簇内放电个数降低.因此,FLC的右移是放电降低的原因.

3.5 簇内ISI的取值与快子系统的极限环的周期有关

抑制性和兴奋性自突触作用下的快子系统的稳定极限环的周期分别如图9(a)和图9(b)所示.不同颜色对应不同的自突触电导, 对某一自突触电导, 左侧较小值对应FLC附近的极限环的周期,右侧较大值对应SNIC附近的极限环的周期.随着抑制性自突触电导的增强, FLC左移, 极限环的范围扩大, 新出现的极限环的周期略有降低的趋势,但差别不大.随着兴奋性自突触电导的增强, FLC右移.无论抑制性还是兴奋性自突触, 同一u值下的极限环的周期差别较小.对于不靠近SNIC的极限环, 其周期不在同u下, 大约为20, 差别也不大.这就是图4所示的簇内ISI差别不大, 大约在20左右的原因.因为簇内峰与快子系统极限环有对应, 簇内峰的ISI与快子系统的极限环有对应.

图9 快子系统的极限环的周期随分岔参数u的变化 (a) 抑制性自突触, 蓝, 绿, 红和黑色曲线分别对应 g =0 , g =0.01 ,g=0.015 和 g =0.02 ; (b) 兴奋性自突触, 蓝、粉、青和棕色曲线分别对应g = 0, g = 0.02, g = 0.03和g = 0.04Fig.9.Period of the limit cycle of the fast system changes with respect to the bifurcation parameter u: (a) Inhibitory autupse.The blue, green, red, and black curves correspond to g =0 , g =0.01 , g =0.015 , and g =0.02 , respectively.(b) Excitatory autupse.The blue, pink, cyan-blue, and brown curves correspond to g = 0, g = 0.02, g = 0.03, and g = 0.04, respectively.

3.6 快子系统的双参数分岔解释反常变化

快子系统在 ( u,g) 平面上的双参数分岔图可以直观地解释自突触作用下放电增强或减弱.抑制性和兴奋性自突触对应的双参数分岔分别如图10中的左列和右列所示.图10中BT为Bogdanov-Takens分岔点, GH为Bautin分岔点, CP为Cusp分岔点, 皆为余维2分岔点.黑、蓝、绿和红线为余维分岔曲线—Hopf, SN, SNIC和FLC分岔曲线.图10(a2)为图10(a1)的放大, 对应本文关注的抑制性自突触的参数范围(0 ≤ g ≤ 0.02).随着抑制性自突触电导强度的增加, 对应SNIC分岔的参数u取值几乎保持不变, 而FLC对应的分岔参数u的取值越来越小, 即FLC左移, 与SNIC对应的分岔参数的范围越来越大, 导致放电参数区间变大、放电增强.图10(b2)是图10(b1)的放大, 对应兴奋性自突触的范围.兴奋性自突触电导强度由0递增至0.04, SNIC的参数几乎不变, 而FLC逐渐右移, 与SNIC距离减小, 导致放电参数区间变窄、放电减弱.

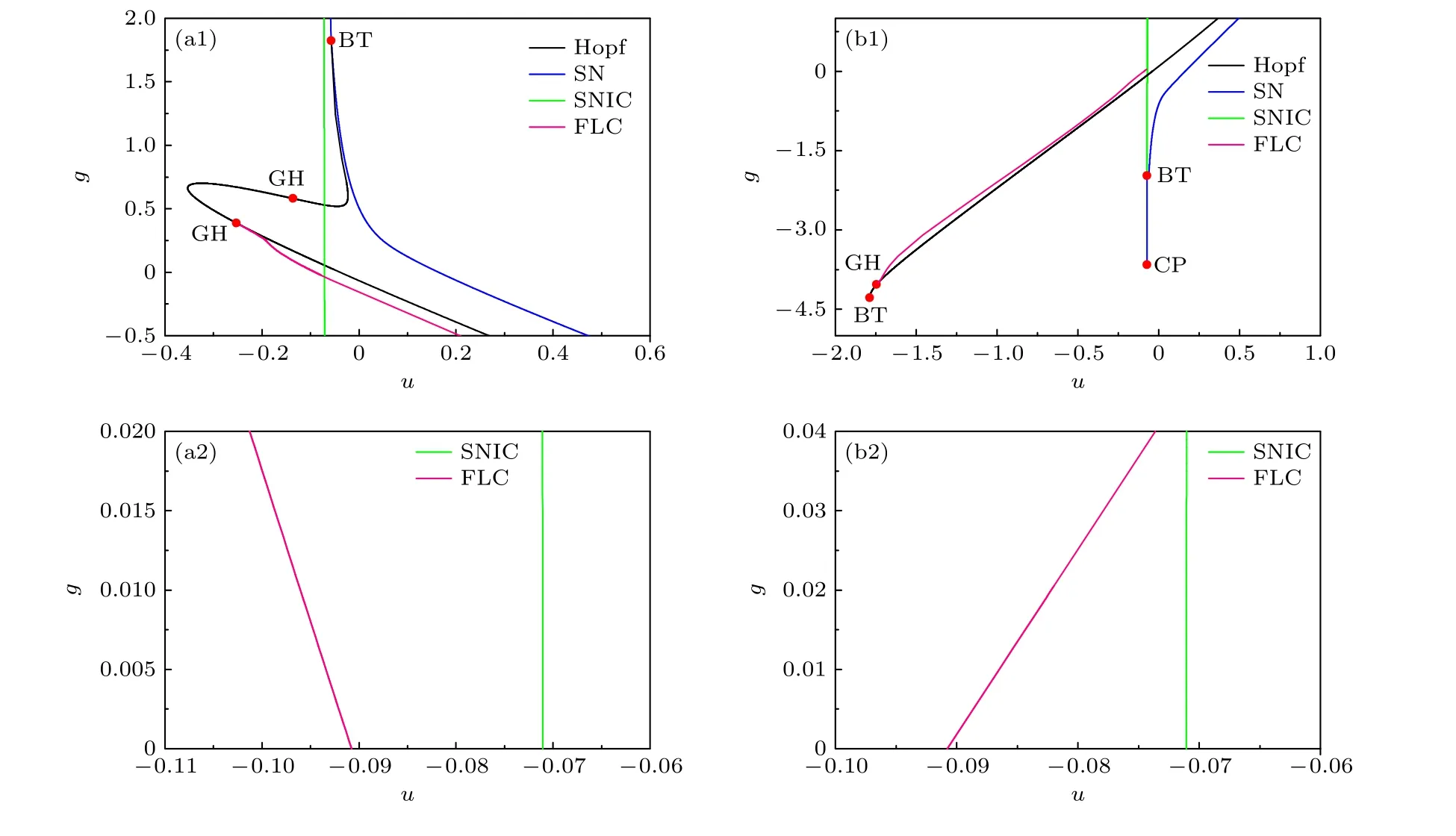
图10 快子系统在 ( u,g) 平面的双参数分岔 (a1) 抑制性自突触; (a2) 图(a1)的局部放大; (b1) 兴奋性自突触; (b2) 图(b1)的局部放大Fig.10.Double-parameter bifurcation in ( u,g) plane of the fast subsystem: (a1) Inhibitory autapse; (a2) enlargement of Fig (a1);(b1) excitatory autapse; (b2) enlargement of Fig (b1).

4 结 论

抑制性或兴奋性作用调控下的簇放电在神经系统的功能实现中起到重要的作用, 因此, 揭示簇放电的动力学及调控机制对于非线性科学和神经科学都有重要的意义.最近研究揭示了多种调控因素下, 特别是自突触调控下的神经电活动的反常变化的机制, 丰富了神经动力学的内涵[17−19,21,24,27,28].本文揭示了兴奋性和抑制性自突触都能引起混合簇放电产生反常现象, 在以下几个方面具有新意.

首先, 扩展了产生反常现象的簇放电的类型.以前研究较多关注了“Fold/Homoclinic”型簇放电以及“Homoclinic/Homoclinic”型簇放电, 簇结束于同宿分岔[18,19,21,49,51].本文关注的混合簇放电属于“Circle/Fold cycle”型簇放电, 复杂之处在于簇结束后会进入去极化阻滞.利用快慢变量分离确认簇结束于极限环的鞍结分岔FLC.该分岔也是去极化阻滞的开始, 在自突触调控诱发反常现象中起到关键作用.

其次, 给出了快自突触诱发反常现象的新示例和分岔机制.对于Chay模型的“Fold/Homoclinic”型簇放电, 只有抑制性快自突触能诱发簇放电的反常现象: 放电增强, 兴奋性快自突触则诱发正常现象, 也是放电增多[18,51].而本文揭示了抑制性和兴奋性作用都能诱发反常现象, 这就给出了反常现象的新示例.此外, “Fold/Homoclinic”型簇放电, 兴奋性和抑制性自突触都能引起放电增多是因为快子系统的同宿分岔的变化方向是相同的[51], 而本文研究的快自突触都能引起反常现象是因为极限环的鞍结分岔的变化方向是相反的.这说明簇结束的极限环的鞍结分岔FLC是引起反常现象的关键因素之一.

最后, 扩展了反常现象及调控机制的多样性.本文的反常现象不仅与以前的快自突触诱发的反常现象不同[18,51], 与具有时滞的自突触(对应慢突触)诱发的簇放电[19,49,50]和峰放电[45,48]的反常现象也不同.以前发现抑制性自突触在合适的时滞下可以增强簇放电或时滞合适的兴奋性自突触可以引起簇放电变弱[19,49,45].本文和以前的研究揭示了快自突触诱发反常现象是因为自突触能调控快子系统的分岔点的位置[18,51], 而具有时滞的自突触诱发的反常现象是自突触电流的作用相位发生改变引起的, 但是快子系统的分岔没变[19,49,50].因此, 本文的研究进一步说明了反常现象具有多样性和多类调控机制.

除了自突触调控, 还有多类其他因素(如具有忆阻器特性的电流)调控的复杂乃至反常的电活动现象及动力学机制[54−56].相较于以前的结果, 本文研究进一步丰富了反常现象的示例和非线性调控机制, 有助于认识神经簇放电特别是混合振荡及自突触的潜在功能.考虑到放电类型特别是簇放电模式也是多样的, 今后可以进一步研究不同因素, 特别是自突触调控不同类簇放电的反常现象及动力学机制, 力争对反常现象建立起更为全面和深入的认识, 促进神经动力学的发展.