解题教学应注重问题的一般化拓展——以一道解析几何题为例

刘海涛 (安徽省芜湖市第一中学 241006)

何浩成 (广东省信宜市信宜中学 525300)

1 试题呈现

题目 已知抛物线C：y2=2px(p>0)的焦点为F，准线l交x轴于点K，过点F作倾斜角为α的直线与C交于A,B两点，若∠AKB=60°，则sinα=

分析 该题形式上为一道以抛物线为背景的解析几何小题，虽结构简单，但内涵丰富、综合性强、解法灵活，主要考查了抛物线的简单几何性质、直线与抛物线的位置关系、三角形的平面几何性质等知识，强化了学生分析问题、解决问题的能力及转化与化归的数学思想，体现了逻辑推理、数学运算、直观想象等数学核心素养.

2 解法探究

评注该法属于解析几何的常规通法，通过联立直线与曲线方程得到一元二次方程，接着利用韦达定理解题，体现“设而不求”的解析几何思想，另外利用向量处理角度问题，体现了向量是几何与代数的“桥梁”的属性，但是该题有点“小题大做”的感觉，计算量大.

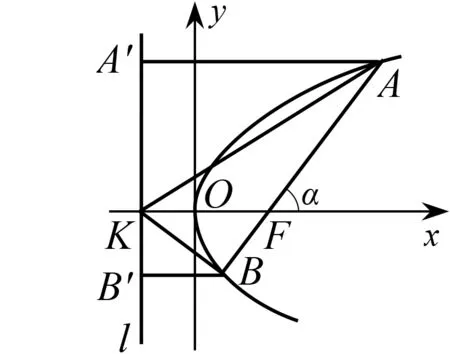
图1

评注该法是对解法2的优化，发现直线KA,KB关于x轴对称这一几何特征，进一步简化解题过程，减少计算，解得简洁明了，体现了“多思少算”的解题策略，给人耳目一新的感觉.

第Ⅱ类的6家研究机构名称及其门户网站名称见表2。显然，从直观的角度来看，门户网站名称和研究机构名称的不一致容易引起受众的混淆，不易使其留下印象。

图2

基于此，我们总结得如下结论：

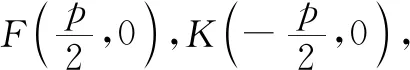
3 一般化拓展

数学家波利亚曾说：“解题就像采蘑菇一样，当我们发现一个蘑菇时，它的周围可能有一个蘑菇圈.”基于结论1，笔者有如下拓展：

结论2已知抛物线y2=2px(p>0)，点P(-m,0)，Q(m,0)(m≠0)，过点P的直线(不与坐标轴垂直)交抛物线于M,A两点，直线MQ,AQ与抛物线的另一交点分别为N,B.①P,B,N三点共线;②直线PA,PB关于x轴对称;③直线MN,AB关于x轴对称.以①②③中任意两个为条件可以推出余下一个.

下面给出由①②推出③的证明过程，另两种情况类似可得.

证明直线PA,PB关于x轴对称，又抛物线y2=2px也关于x轴对称，故点M与B、点N与A关于x轴对称，易知直线MN,AB关于x轴对称.

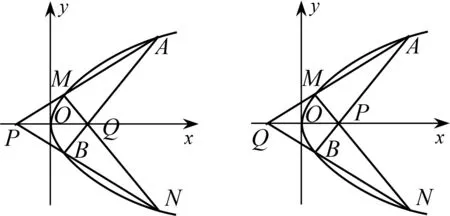
图3 图4

圆锥曲线不限于抛物线，还有椭圆和双曲线，基于上述研究，笔者借助几何画板探究椭圆与双曲线，发现也有类似上述结论.

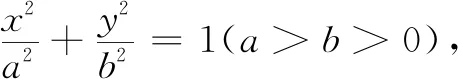
说明结论3的证明参照结论2.当|m|>a时，结论3如图5和6所示；当|n|>a时，结论3如图7和8所示.

图5 图6

图7 图8

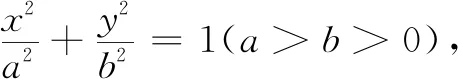
说明结论4的证明参照结论2.我们知道椭圆与圆之间可以由伸缩变换得到[1]，令a2=b2，即得以坐标原点为圆心、a为半径的圆，所以结论3与4在圆中也成立.

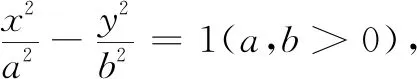
说明结论5的证明参照结论2.当|m|>a时，结论5如图9和10所示；当|n|>a时，结论5如图11和12所示.

图9 图10

图11 图12

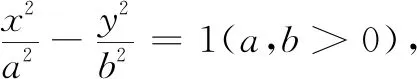
说明结论6的证明参照结论2.结论6如图13所示.

图13

4 归纳总结

笔者在文[3]中介绍了极点与极线的知识，不难发现点Q为点P对应的极线与坐标轴的交点，点P为点Q对应的极线与坐标轴的交点，即“伴侣点”中的一点为另一点对应的极线与伴侣点所在坐标轴的交点，于是得到如下结论：

结论8已知P,Q两点为曲线(椭圆、双曲线、抛物线、圆)的一对“伴侣点”，过点P的直线(不与坐标轴垂直)交曲线于M,A两点，直线MQ,AQ与双曲线的另一交点分别为N,B.①P,B,N三点共线;②直线PA,PB关于x(或y)轴对称;③直线MN,AB关于x(或y)轴对称.以①②③中任意两个为条件可以推出余下一个.