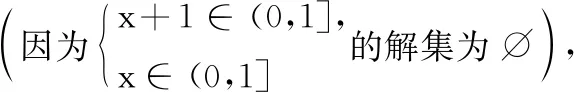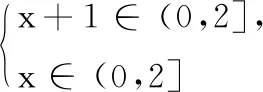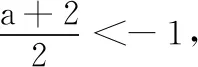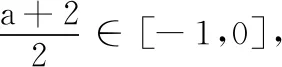对一道函数试题的质疑
李瑞华 (江苏省南京市六合区程桥高级中学 211504)
王安寓 (江苏省南京市六合区实验高级中学 211500)
临近高一上学期期末,高一年级数学组组织教师编撰了3套高一数学上学期期末模拟试卷,其中选了一道高难度的函数恒成立问题(题目1)作为第3套试卷的压轴题,同时,题目1也是2018—2019年度南京市高一上学期期末统考试题的第20题(试卷压轴题).笔者在独立解答时发现,题目1存在瑕疵.下面,笔者将对题目1的疑惑整理成文,与读者交流.
1 题目呈现,简要分析
题目1(2018—2019南京高一上期末试卷)给定区间I,集合M是满足下列性质的函数f(x)的集合:任意x∈I,f(x+1)>2f(x).
(1)已知I=R,f(x)=3x,求证:f(x)∈M;
(2)已知I=(0,1],g(x)=a+log2x,设g(x)∈M,求实数a的取值范围;
(3)已知I=[-1,1],h(x)=x2+ax+a-5(a∈R),讨论h(x)与集合M的关系.
标准答案 (1)f(x+1)-2f(x)=3x+1-2×3x=3x>0,故f(x+1)>2f(x),从而f(x)∈M.
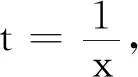
(3)若h(x)∈M,则当x∈[-1,1]时,h(x+1)>2h(x)恒成立,即-(x+1)2+a(x+1)+a-5>2(-x2+ax+a-5)恒成立,即x2-ax-2x+4>0恒成立.记H(x)=x2-ax-2x+4,x∈[-1,1].
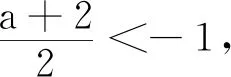

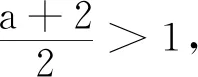
综上,-7 所以,当-7 第(1)问的求解是正确的.由于f(x)=3x的定义域是R,所以f(x+1)的定义域也是R,问题转化为对任意的实数x,f(x+1)>2f(x)恒成立,用比较中的最基本方法——作差法求解即可(标准答案中正是如此求解). 第(2)(3)问的求解,笔者认为是存在瑕疵的.先从形的角度对第(2)问作简要分析. 作出y=g(x),y=g(x+1),y=2g(x)的图象,我们从图象上观察,研究y=g(x+1)与y=2g(x)的函数值的大小关系. 对于不等式g(x+1)>2g(x),有两种不同的思考切入点.①g(x+1)与2g(x)中的x不是同一个x,二者互不相干,即它们是两个自由的变量;②g(x+1)与2g(x)中的x是同一个x. 先看思考切入点①.g(x+1)与2g(x)中的x不是同一个x,两个x是自由的量,没有关系,那么g(x+1)>2g(x),就相当于g(x1+1)>2g(x2)对任意的x1,x2∈(0,1]都成立.由恒成立的知识知g(x1+1)min>2g(x2)max,反映到图象上,y=g(x+1)的图象的所有点都在y=2g(x)的图象的上方.我们知道,y=g(x+1)的图象是由y=g(x)的图象向左平移一个单位而得到,y=2g(x)的图象是由y=g(x)的图象上各点横坐标不变、纵坐标伸长到原来的2倍而得到.左右平移时,不改变函数的值域——y值不变,因此,y=g(x+1)的值域与y=g(x)的值域相同.沿y轴伸缩会影响函数值域,因此,y=2g(x)的值域是y=g(x)的值域的2倍. 当a=0时(图1),y=g(x+1)的值域与y=2g(x)的值域相同,那么g(x+1)>2g(x)恒成立是错误的; 当a<0时(图2),y=2g(x)的值域y=g(x+1)的值域,那么g(x+1)>2g(x)恒成立是错误的; 当0 综上,当a<1时g(x+1)>2g(x)是不能恒成立的. 图1 图2 图3 图4 读者会说,在一个式子中,相同的字母含义是相同的,即应该是思考切入点②:g(x+1)与2g(x)中的x是同一个x.众所周知,g(x)>f(x)对x∈I恒成立,反映到图象上,就是对任意的x∈I,函数y=g(x)的图象在函数y=f(x)的图象上方.任意的x∈I,g(x)>f(x),即任意的x0∈I,当x=x0∈I时,g(x0)>f(x0).反映到图象上,就是直线x=x0与y=g(x)的图象交于点P(x0,g(x0)),直线x=x0与y=f(x)的图象交于点Q(x0,f(x0)),则点P在点Q上方. 我们来看第(2)问中两个函数y=g(x+1),y=2g(x)的图象,以a=0的图象为代表(图4,另两类可一样操作),作出直线x=x0(x0∈(0,1)),我们直观地看到,直线x=x0与y=g(x+1)的图象没有交点,与y=2g(x)的图象有一个交点;没有交点和有一个交点,如何比较交点位置? 由此可以看出,两种思考切入点都是存在问题的,从而第(2)问的解答是存在瑕疵的.那么是题目错了,还是解答过程出错了?还有别的解法吗?还有新的思考切入点吗? 命题人的意图是好的,想考查学生应用分离参数法解决恒成立问题,想考查重要的对数函数的性质、对数运算(从标准答案也能看出),但是标准答案是错误的,或者说是有瑕疵的.为找到错误的根源,我们再来回顾以下几道题目. 与题目1的第(2)(3)问一样要注意函数定义域的题目有很多.举例如下: 题目2已知函数f(x)=log3x,x∈[1,9],求函数y=[f(x)]2+f(x2)的最大值. 题目3函数y=lg(x2-2x-3)的单调递增区间是( ). A.(-∞,1) B.(-∞,-1) C.(1,+∞) D.(3,+∞) 简解 由x2-2x-3>0得x<-1或x>3,故函数y的定义域是{x|x<-1或x>3}.因为u=x2-2x-3在x<1时递减,在x>3时递增,y=lgu在u>0时递增,且当x<-1或x>3时u>0,所以y=lg(x2-2x-3)的单调递减区间是(-∞,-1),单调递增区间是(3,+∞),故选D. 评注在求解题目3时,有部分学生错选了C.造成错选的原因很简单——学生忘记在函数定义域内研究函数的单调性.这种错误,每位教师上课时都会强调,且不只一次地强调.但是轮到考试,总会有学生错选.而遇到更隐秘的函数问题时,甚至部分教师也将函数定义域“束之高阁”.如题目1的第(2)(3)问.也就是说,笔者认为,题目1第(2)(3)问是遗忘了研究使式子有意义的x的范围. 题目4不等式ln(x2-1)>ln(1-x)的解集为. 简解 原不等式等价于x2-1>1-x>0,解得x<-2.故原不等式的解集为(-∞,-2). 评注解不等式时首先要保证不等式中各式子有意义(即存在),然后再解不等式.题目4还可以改变试题的呈现方式,得题目5. 题目5已知函数f(x)=lnx,则不等式f(x2-1)>f(1-x)的解集为. 简解 易知函数f(x)在定义域(0,+∞)上单调递增,故原不等式可化为x2-1>1-x>0,解之得x<-2,故原不等式的解集为{x|x<-2}. 评注求解题目5时,保证不等式中各式子都有意义,再应用函数单调性去掉法则f,转化为简单的一元一次、一元二次不等式组求解.如同 题目2~题目4一样,极易忽视函数定义域. 我们将题目5中的函数解析式隐去,用抽象函数命制,得到题目6. 题目6已知定义在区间(-1,1)上的奇函数f(x)在[0,1)上单调递减,则不等式f(m-1)+f(m2-1)>0的解集为. 评注无论是抽象函数不等式还是显性函数不等式,求解时都必须保证不等式中各式子有意义.无论是函数值域单调性还是解函数不等式,都离不开函数的定义域. 由题目2~题目6,我们应能想到题目1的第(2)(3)问的求解的瑕疵所在——没有考虑式子f(x+1)>2f(x)中各部分有意义,即x+1和x都得属于I. 题目7给定区间I,集合M是满足下列性质的函数f(x)的集合:任意x∈I,f(x+1)>2f(x). (1)已知I=R,f(x)=3x,求证:f(x)∈M; (2)已知I=(0,2],g(x)=a+log2x,设g(x)∈M,求实数a的取值范围. 对题目1第(3)问的解答做修改(题目不变): 综上,a>-7. 所以,当a>-7时h(x)∈M;当a≤-7时h(x)∉M. 由对题目1第(2)(3)问的质疑,我们再次感受到函数定义域的重要性.在求解函数问题时,一定要记得先求函数的定义域,特别是以复合函数形式出现的题目.

2 类题再现,寻根求源
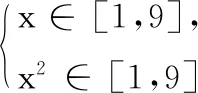
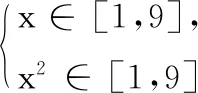
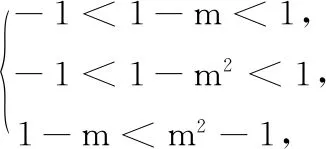
3 对题目1第(2)(3)问的修改